2. 中国环境科学研究院, 国家环境保护饮用水水源地保护重点实验室, 北京 100012;
3. 云南省高原湖泊流域污染过程与管理重点实验室, 昆明 650034
2. State Environmental Protection Key Laboratory of Drinking Water Source Protection, Chinese Research Academy of Environmental Sciences, Beijing 100012;
3. Yunnan Key Laboratory of Pollution Process and Management of Plateau Lake-Watershed, Kunming 650034
识别湖泊水质时空变化特征, 对于评价流域污染防治效果, 确定流域污染防治措施具有重要意义(Jones et al., 2008).目前, 用于水质时空变化特征识别的统计学方法主要包括2类:①方差分析, 该方法用于判定水质时空差异的显著性(周丰等, 2007; 富天乙等, 2014);②非参数方法, 用于判定水质时空变化趋势的显著性, 例如Kendall趋势检验法、季节性Kendall趋势检验法、Daniel趋势检验法等(高伟等, 2013; 李文赞等, 2013).方差分析需要满足正态、独立、同方差的假设, 而这些假设有时不能满足(Qian & Shen, 2007; Behm et al., 2013), 且方差分析难于处理具有嵌套结构的数据(Schielzeth & Nakagawa, 2013);非参数方法则通过秩变换造成信息损失(Smith et al., 2003).此外, 上述两种方法只能给出差异或趋势显著性的结果, 不能直接反映水质的时空动态特征.
贝叶斯方差分析模型(Bayesian ANOVA)是一种采用贝叶斯理论进行参数估计、具有层次结构的方差分解方法(Tiao & Box, 1967; Khuri & Sahai, 1985; Gelman, 2005).该模型将总方差分解为因子组分和残差组分, 并对因变量在各因子水平下的效应值(即某一特定水平下的平均值与总平均值的差值)进行估计.该模型具有灵活的结构, 适用的总体不限于正态分布, 可有效地解决自相关和异方差问题(Qian and Shen, 2007; Collins et al., 2010;Smith et al., 2012).此外, 该方法还具有如下优点:①可方便地融合先验知识, 并对参数进行不确定性分析(Fordyce et al., 2011);②由于模型的层次结构, 估计特定水平的效应值时可从其它水平的观测值中“借力(Borrow Strength)”, 使得个体平均值向总平均值收缩, 提高参数估计的精确度, 降低决策的不确定性(Oldenkamp et al., 2015;Qian et al., 2015a).该方法在研究中被引起关注始于Gelman (2005)对其原理的系统阐述, 及Qian等(2007)对其在生态学领域中的开拓性研究.目前, 该方法已得到广泛应用:包括①因子的显著性检验(Brousseau et al., 2013);②因子的相对重要性比较(DuFour et al., 2014);③因子的动态性特征识别(Qian et al., 2009)等.
贝叶斯方差分析的上述特点和优势适用于水质时空变化特征的识别.然而已有的研究相对较少, 主要限制于较长的运算时间.近年来, 随着算法的开发与进步, 贝叶斯方差分析已可方便快捷地实现(Monnahan et al., 2017).本研究提出了基于贝叶斯方差分析方法的湖泊水质时空变化特征识别的方法步骤;以异龙湖稳态转换条件下富营养化指标浓度的变化特征和滇池外海特征污染物浓度达标率的时空变化特征为例, 探究该方法在对数正态分布(Qian, 2015)和二项分布(梁中耀等, 2017)总体的适应性.针对参数的可交换性假设被忽视的问题, 本研究提出一种基于模型选择准则的判定方法并将其应用于滇池案例中.
2 材料与方法(Materials and methodology) 2.1 基于贝叶斯方差分析的湖泊水质时空变化特征识别步骤基于贝叶斯方差分析的基本原理(Gelman & Tuerlinckx, 2000; Gelman, 2005), 本文提出基于贝叶斯方差分析方法的湖泊水质时空变化特征识别的一般步骤(图 1):①根据因变量的数据特征确定总体的分布形式, 有时需要对数据进行变换, 例如有些水质变量的值可通过对数变换转换为正态分布, 而在探究变量达标率时则通常需要将监测数据转化为{0, 1}变量.②确定模型的结构.当有多个因子时, 需要对因子之间的关系进行分析, 如果因子之间是包含关系则需要建立具有嵌套结构的模型;如果因子之间不存在包含关系, 则需要建立具有交叉因子的模型, 并考虑因子间的交互作用.③分析因子效应的可交换性.参数的可交换性假设决定了在对因子不同水平效应值进行估计时是否应采用层次模型的形式.④参数估计.贝叶斯方差分析模型可通过Markov Chain Monte Carlo(MCMC)方法对参数的后验分布进行估计(茆诗松和汤银才, 2012), 该算法可在BUGS系列软件(如WinBUGS、JAGS等)中实现.近年来, 采用Hamiltonian Monte Carlo(HMC, 一种高效的贝叶斯推断方法)进行参数估计的Stan软件被开发出来(Gelman et al., 2015; Carpenter et al., 2017), 对于复杂的、具有层次结构的贝叶斯模型, Stan具有更高的运算效率(Monnahan et al., 2017);此外, 采用极大似然估计(ML)的广义线性混合模型(GLMM)也可作为贝叶斯方差分析模型参数的近似估计(Qian et al., 2010).上述方法均可方便地在R软件中运行或调用(表 1).⑤根据参数的后验分布和研究目的, 进行统计推断.
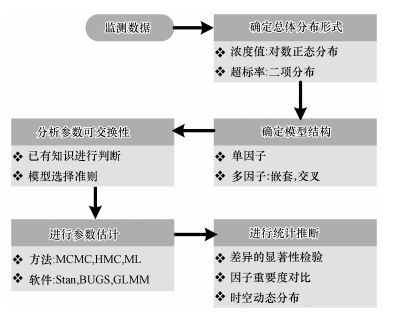 |
| 图 1 技术路线 Fig. 1 Framework to identify temporal and seasonal dynamics of lake water quality based on Bayesian ANOVA |
| 表 1 常用的贝叶斯分析软件及其与R软件的接口 Table 1 Common used software/methods for parameters estimation based on Bayesian statistics and their interface with R software |
为验证上述方法在湖泊水质时空变化特征识别中的适用性, 本文选择了2种环境科学和生态学研究中最为常见的分布(正态分布和二项分布), 以异龙湖和滇池2个案例对上述方法的基本原理和步骤进行展示.
2.2 案例1:异龙湖在两种稳态时富营养化指标浓度变化特征分析云南省异龙湖在2009年发生了由草型清水稳态向藻型浊水稳态的转换(Zhao et al., 2013).为探究两种稳态条件下异龙湖富营养化指标叶绿素a(Chla)、总氮(TN)和总磷(TP)浓度的变化特征, 收集了2004—2013年的常规水质监测数据, 频次为每月1次, 共有120组数据.
3种富营养化指标经过对数变换后可认为服从正态分布(Qian, 2015), 因而先对监测数据进行对数变换.考虑到水质指标存在年际波动, 选择稳态状态和年份作为关注的因子;由于稳态状态包含不同的年份, 即二者是包含关系, 因而应建立具有嵌套结构的方差分析模型.由于异龙湖在稳态转换发生后大型水生植物消失, 生态系统的结构发生了剧变, 营养盐的浓度也大幅增加(Zhao et al., 2013), 因而假设变量在两种稳态时的参数是不可交换的;由于在某种特定的稳态条件下, 营养盐指标的浓度相对稳定且研究的年份较短, 因而假设年平均值在特定的稳态条件下是可交换的.本案例采用的贝叶斯方差分析模型如下(式(1)~(2)).
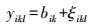
|
(1) |
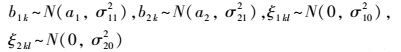
|
(2) |
式中, i为稳态标识(i =1为清水稳态, i =2为浊水稳态), k为年份标识(当i =1时k =1~5, 表示2004—2008年;当i =2时k =6~10, 表示2009—2013年), l为月份标识, 代表每年的12个月;yikl为对数变换后的水质指标值;a1、a2分别为清水稳态、浊水稳态时的多年平均值;b1k、b2k分别为清水稳态、浊水稳态的年平均值, 分别服从均值为a1、a2, 标准差为σ11、σ21的正态分布;ξ1kl、ξ2kl分别为清水稳态、浊水稳态的残差, 代表年内波动和其它随机波动, 服从均值为零、标准差分别为σ10、σ20的正态分布.该模型以稳态状态将水质指标的波动分为2个阶段, 每阶段的波动又被分成年际波动(σ112和σ212)和残差(σ102和σ202)2个部分, 总方差分别为σ12=σ112+σ102和σ22=σ212+σ202.
采用R软件中的rstan软件包(Stan Development Team, 2016)进行模型构建和参数估计, 该软件包采用HMC算法进行参数估计.对于待估参数a1、a2、σ11、σ21、σ10、σ20, 采用无信息先验.共运行4条链, 每条链的迭代次数为50000次, 其中前25000次用于预热, 后25000次用于获得参数的后验分布.采用统计量R_hat≈1.0来保证链的收敛(Gelman & Hill, 2007).本案例的主要研究内容为:根据参数的后验分布, ①对两种稳态条件下3种指标的浓度差异进行显著性检验, ②分析两种稳态时年际方差比例的变化(分别为σ112/σ12和σ212/σ22).
2.3 案例2:滇池外海TN浓度达标率的时空变化特征本案例选择滇池典型污染物(TN)浓度达标率为研究对象, 收集滇池外海2007—2016年8个常规监测站点的监测数据, 监测频次为每月1次, 以年份和站点为因子变量, 探究TN浓度达标率(以V类水质限值为标准值, 即为2 mg·L-1)的时空变化特征.
首先将监测数据转化为{0, 1}变量, 即当TN浓度大于2 mg·L-1时水质不达标, 记为1, 否则记为0.然后计数得到每个站点每年的超标样本数, 记为zSY (S为站点, Y为年份), 总样本数量记为nSY (由于每个站点每年均有12组监测数据, 故nSY为12).由于年份和站点之间不存在包含关系, 因而应建立交叉因子结构的模型.由于缺乏对该模型中站点和年份因子的效应值是否具有可交换性的知识, 本研究提出一种基于模型选择准则的参数可交换性假设判定方法, 即首先建立参数可交换模型和参数不可交换模型, 然后求出衡量模型表现的统计量, 最后通过选择最佳模型来判定参数的可交换性;如果有多个因子, 则需考虑各种不同的组合.本案例采用GLMM方法进行参数估计;模型的选择准则需要同时考虑变量个数和拟合效果, 因而选择AIC(Akaike′s information criterion)和BIC(Bayesian information criterion)作为模型的选择准则, AIC和BIC值越低则表明对应的模型越好(Hooten & Hobbs, 2015; Aho et al., 2017).本案例共有2个因子, 因而共建立22=4个备选模型(表 4), 建立的贝叶斯方差分析模型如下:
| 表 4 备选模型组成及其模拟效果 Table 4 Structures of candidate models and model performances |
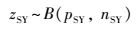
|
(3) |
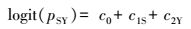
|
(4) |
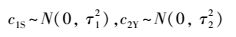
|
(5) |
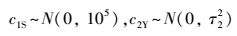
|
(6) |
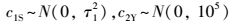
|
(7) |
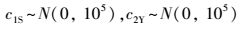
|
(8) |
式(3)表示zSY服从成功概率为pSY、试验次数为nSY=12的二项分布;二项分布的连接函数为logit函数, 满足logit(pSY)=ln(pSY/(1- pSY)), 则logit(pSY)的取值范围为(-∞, +∞), 其中c0表示平均达标率, c1S和c2Y分别表示站点和年份的因子效应.在式(6)~(8)中, 当参数服从方差待估计的先验分布时, 表明参数是可交换的, 即c1S ~N(0, τ12)和c2Y ~N(0, τ22);当参数服从已知的先验分布时, 表明参数是不可交换的, 即c1S ~N(0, 105)和c2Y ~N(0, 105).
采用R软件中的lme4软件包中的glmer函数进行模型构建和参数估计.本案例的主要研究内容为:根据模型选择准则和参数估计结果, ①分析站点和年份2个因子效应参数的可交换性, ②比较站点和年份因子对TN超标率波动影响的相对大小, ③分析TN超标率的时空变化特征.
3 结果(Results) 3.1 案例1:异龙湖在两种稳态时富营养化指标浓度变化特征分析异龙湖富营养化指标方差分析模型的参数估计结果可以分为3类(表 2):①均值, 表征两种稳态条件下富营养化指标的平均值;②方差, 表征年份与残差对富营养化指标波动的贡献;③年平均值, 表征富营养化指标的年际变化特征.贝叶斯方差分析模型清晰地展示了富营养化指标在两种稳态时的均值和方差组成, 及指标的年际变化.
| 表 2 异龙湖富营养化指标方差分析模型的参数估计结果 Table 2 Parameters estimation of the Bayesian ANOVA model for the three viables indicating the trophic state in Lake Yilong |
根据参数的后验分布, 采用随机变量模拟的方法(Kerman & Gelman, 2007), 对两种稳态条件下平均值的差异(即为a2-a1)进行显著性检验, 发现3种指标平均值差异的95%置信区间均不包含零(图 2), 表明稳态转换前后3种富营养化指标浓度的平均值发生了显著变化;由于95%置信区间的下限均大于零, 表明浊水稳态时的平均值显著变大.3种指标的组间方差占总方差的百分比在浊水稳态时均变小(表 3), 表明年份作为因子对于指标波动的影响减弱;尤其是对于TP和Chla浓度, 浊水稳态时的组间方差比例仅为17%和2%.
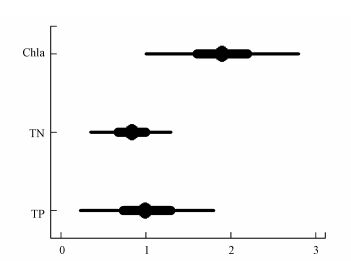 |
| 图 2 异龙湖稳态转换前后富营养化指标的差异 (对数尺度)(圆点代表浊水稳态与清水稳态差异的平均值, 较宽的线条表示50%置信区间, 较窄的线条表示95%置信区间) Fig. 2 Differences of the three indexes indicating the trophic state between turbid state and clear state in Lake Yilong |
| 表 3 异龙湖3种富营养化指标在两种稳态条件下的年际方差比例 Table 3 Ratios of inter-annual variance to the total variance of three variables indicating trophic state under clear state and turbid state in Lake Yilong |
本案例验证了基于贝叶斯方差分析的湖泊水质时空变化特征识别方法在正态分布总体的适用性, 表明贝叶斯方法分析模型可以方便地区分稳态因子平均值和年平均值, 处理具有嵌套结构的数据.案例分析结果表明, 异龙湖的富营养化状态发生了剧烈的恶化, 而浊水稳态的年际方差比例很小则说明异龙湖的富营养化问题仍未得到有效控制.因而, 异龙湖的富营养化问题急需强有力的防治措施.此外, 两种稳态时年际方差比例差异性较大, 这为认知稳态转换的水质指标变化特征提供了参考, 其原因值得进一步探究.
3.2 案例2:滇池外海TN浓度达标率的时空变化特征识别本研究建立了4个不同的贝叶斯方差分析模型, 用于探究滇池外海TN浓度超标率的时空变化特征.模型评价结果显示, 模型3具有最小的AIC值和BIC值(表 4), 表明其为用于表征滇池外海TN浓度超标率时空变化特征的最佳模型.该结果说明TN浓度超标率在站点间是可交换的, 而在年份之间则不可交换.
根据模型3的参数估计结果, 可得年份之间的方差和站点之间的方差分别为0.923和0.006(表 5).对比可知, 年份之间的方差(0.923)远大于站点之间的方差(0.006), 因而年份是影响滇池外海TN浓度达标率变化的主要因子, 而站点的影响则很小, 即TN浓度的达标率具有较强的时间波动, 而空间差异则很小.
| 表 5 滇池外海TN浓度超标率方差分解结果 Table 5 Variance component for incompliance ratio of the TN concentration in Lake Dianchi |
由于方差分析模型直接估计的是logit变换之后的变量值, 不能直接用于展示TN达标率的时空变化特征, 本研究采用随机变量模拟的方法对变量进行logit变换的逆变换(Kerman & Gelman, 2007), 得到TN浓度超标率的时空变化特征及其不确定性(图 3).在时间尺度上, TN浓度的超标率可分为两段:2007—2013年为较高超标率阶段, 2014—2016年为较低超标率阶段.滇池外海TN浓度在近3年来得到了较好的控制, 处于劣V类水质的平均概率由以往的40%左右降到了10%左右(图 3a).在空间尺度上, TN浓度的超标率没有明显的空间差异(图 3b).
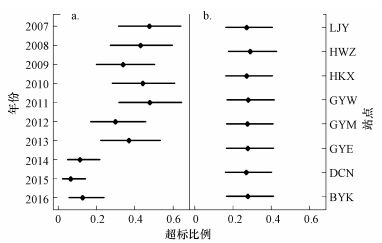 |
| 图 3 滇池外海TN超标率时空变化特征 (圆点代表平均值, 线条表示95%置信区间) Fig. 3 Temporal (a) and spatial (b) characters of the incompliance ratio of TN concentration in Waihai part, Lake Dianchi |
本案例验证了基于贝叶斯方差分析的湖泊水质时空变化特征识别方法在二项分布总体的适用性.案例分析结果表明, 滇池外海TN的超标率明显下降, 说明流域污染防治的效果初步显现;而超标率在空间上差异很小, 说明滇池外海TN超标率的空间变化具有很好的一致性.
4 讨论(Discussion) 4.1 贝叶斯方差分析模型参数的可交换性贝叶斯方差分析模型是一种自变量均为因子变量的层次模型.在进行参数估计时, 贝叶斯层次模型通过借力来提高参数估计的精确度.这种思想最早来源于Stein的参数估计理论(Stein, 1955; Efron & Morris, 1977), 即:对某一特定个体平均值的估计不再采用最佳线性无偏估计的形式, 而是将这种最佳线性无偏估计向包含其它个体的总平均值收缩.最佳线性无偏估计只注重参数估计的准确度, Stein的参数思想则对准确度和精确度并重, 是对二者的权衡.贝叶斯层次模型是Stein的参数估计思想的一种特殊形式, 特定个体的平均值向总平均值的收缩程度由组内方差和组间方差的相对大小决定.理论研究表明, 贝叶斯层次模型得到的平均值的估计值具有更高的准确度(Qian et al., 2015b).
Stein的参数估计思想及贝叶斯层次模型对参数的估计过程是建立在参数的可交换性的基础上的, 当参数为非可交换性时仍采用贝叶斯层次模型会造成向总平均值的过度收缩(Neuenschwander et al., 2015).参数的可交换性这一假设在环境科学和生态学的应用中常常被忽视, 大部分已有文献缺乏对参数可交换性的验证或者说明.Qian等(2015b)认为参数的可交换与否需根据已有的知识进行谨慎地推断, 本研究中的案例1即采用这样的方法.而在缺乏对研究区域的系统认知和判断的条件下, 本研究在案例2中提出一种基于模型选择准则的方法, 即通过构建多个可能的模型, 通过模型选择准则推断参数是否具有可交换性.案例2采用的是广义线性混合模型, 因而选择的判别准则是AIC和BIC;当采用贝叶斯方法进行参数估计时, 可供选择的包括DIC、WAIC和LooIC等(Vehtari et al., 2016).显然, 依据判别准则来确定参数的可交换性可以降低主观因素对参数可交换性判定的干扰(Atkinson et al., 1992).
4.2 贝叶斯方差分析适用性的评价采用统计学假设检验的方法简单地回答因子“是否”影响因变量已经不能满足生态学研究的需要, 研究者更加关注的是回答影响的“正负”以及变化了“多少”的问题(梁中耀等, 2014; Touchon & McCoy, 2016).本研究的结果表明, 贝叶斯方差分析方法除可进行因子对因变量影响的显著性检验(案例1)外, 还可用于探究因子的重要性和展示时空变化特征(案例2).
虽然与均值同为描述随机变量特征的统计量, 然而长期以来方差却没有引起生态学研究的足够重视(Nakagawa & Schielzeth, 2012; Violle et al., 2012).近年来, 群落生态学和个体生态学研究中开始强调方差的重要性, 例如Bolnick等(2011)总结和识别出在群落生态学中性状的种内变异性会导致生态相互作用发生改变的6种机制, Cleasby等(2014)指出研究个体性状变异和个体间性状变异的相对大小对于衡量个体性状的重要性具有重要意义.在水质评价中, 指标的波动性变小被认为是生态系统恢复的体现(Sharpley et al., 2013).而本研究发现, 相对于清水稳态, 异龙湖处于浊水稳态时年际方差的相对贡献率减小;滇池外海8个监测站点的TN超标率的波动性在2014—2016年明显变小.水质变量波动性的变化特征及不同层级的因子对波动性的贡献特征, 也是水质时空变化特征的重要表现.显然, 贝叶斯方差分析适用于方差的时空动态性分析.
案例研究表明贝叶斯方差分析模型是一种适用于环境科学和生态学研究最新需求的统计学方法, 在进行因子显著性检验时可用于替代经典的方差分析方法, 而在探索性分析中可有效处理与方差分解相关的问题.此外, 关于贝叶斯估值理论和软件的发展与进步使得贝叶斯方差分析更加简捷(例如本研究所案例的运行时间均在5 min以内), 使得该方法不再受限于计算效率的问题.更重要的是, 随着水质监测数据的累积和监测时空精度的增加, 识别不同时空尺度下的水质变化特征的需求日益突出, 因而贝叶斯方差分析具有广阔的应用前景.
5 结论(Conclusions)在进行贝叶斯方差分析时, 参数的可交换性通常被忽视.除根据已有知识进行判断外, 本研究在案例2中提出了一种基于模型判别准则的方法, 降低了参数可交换性判别时的主观性.
本文阐述了基于贝叶斯方差分析方法进行湖泊水质时空变化特征识别的一般步骤, 并通过2个案例分别验证了其在识别水质变量浓度值的时空变化特征和达标率的时空变化特征时的适用性.研究表明, 贝叶斯方差分析方法可适用于具有嵌套结构的数据;除了可进行因子对因变量影响的显著性检验外, 还可以比较因子的相对重要程度, 探究因变量在不同因子水平下的变化特征.随着水质监测数据的累积和监测时空精度的增加, 贝叶斯方差分析模型具有广阔的应用前景.
案例研究结果表明, 相对于清水稳态时, 异龙湖在浊水稳态时3种富营养化指标具有更高的浓度值, 且年际方差比例明显减小;滇池外海TN浓度超标率由前7年(2007—2013年)的40%左右降到近3年(2014—2016年)的10%左右, 且波动性降低.
Aho K, Derryberry D, Peterson T. 2017. A graphical framework for model selection criteria and significance tests: refutation, confirmation and ecology[J]. Methods in Ecology and Evolution, 8: 47–56.
DOI:10.1111/mee3.2017.8.issue-1
|
Atkinson S E, Crocker T D, Shogren J F. 1992. Bayesian exchangeability, benefit transfer, and research efficiency[J]. Water Resources Research, 28: 715–722.
DOI:10.1029/91WR02598
|
Behm J E, Edmonds D A, Harmon J P, et al. 2013. Multilevel statistical models and the analysis of experimental data[J]. Ecology, 94: 1479–1486.
DOI:10.1890/12-2005.1
|
Bolnick D I, Amarasekare P, Araújo M S, et al. 2011. Why intraspecific trait variation matters in community ecology[J]. Trends in Ecology & Evolution, 26: 183–192.
|
Brousseau L, Bonal D, Cigna J, et al. 2013. Highly local environmental variability promotes intrapopulation divergence of quantitative traits: an example from tropical rain forest trees[J]. Annals of Botany, 112: 1169–1179.
DOI:10.1093/aob/mct176
|
Carpenter B, Gelman A, Hoffman M D, et al. 2017. Stan: A Probabilistic Programming Language[J]. Journal of Statistical Software, 76: 1–29.
|
Cleasby I R, Nakagawa S, Schielzeth H. 2014. Quantifying the predictability of behaviour: statistical approaches for the study of between-individual variation in the within-individual variance[J]. Methods in Ecology & Evolution, 6: 27–37.
|
Collins A, Hart E M, Molofsky J. 2010. Differential response to frequency-dependent interactions: an experimental test using genotypes of an invasive grass[J]. Oecologia, 164: 959–969.
DOI:10.1007/s00442-010-1719-9
|
DuFour M R, Pritt J J, Mayer C M, et al. 2014. Bayesian hierarchical modeling of larval walleye (Sander vitreus) abundance and mortality: Accounting for spatial and temporal variability on a large river[J]. Journal of Great Lakes Research, 40: 29–40.
DOI:10.1016/j.jglr.2014.08.001
|
Efron B, Morris C. 1977. Stein's paradox in statistics[J]. Scientific American, 236: 119–127.
DOI:10.1038/scientificamerican0577-119
|
Fordyce J A, Gompert Z, Forister M L, et al. 2011. A hierarchical bayesian approach to ecological count data: A flexible tool for ecologists[J]. Plos One, 6: e26785.
DOI:10.1371/journal.pone.0026785
|
富天乙, 邹志红, 王晓静. 2014. 基于多元统计和水质标识指数的辽阳太子河水质评价研究[J]. 环境科学学报, 2014, 34(2): 473–480.
|
Gelman A, Hill J. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models[M]. Cambridge University Press, New York.
|
Gelman A, Lee D, Guo J. 2015. Stan: A Probabilistic Programming Language for Bayesian Inference and Optimization[J]. Journal of Educational and Behavioral Statistics, 40: 530–543.
DOI:10.3102/1076998615606113
|
Gelman A, Tuerlinckx F. 2000. Type S error rates for classical and Bayesian single and multiple comparison procedures[J]. Computational Statistics, 15: 373–390.
DOI:10.1007/s001800000040
|
Gelman A. 2005. Analysis of variance-why it is more important than ever[J]. Annals of Statistics, 33: 39–42.
|
高伟, 陈岩, 徐敏, 等. 2013. 抚仙湖水质变化(1980-2011年)趋势与驱动力分析[J]. 湖泊科学, 2013, 25: 635–642.
DOI:10.18307/2013.0503 |
Hooten M B, Hobbs N T. 2015. A guide to Bayesian model selection for ecologists[J]. Ecological Monographs, 85: 3–28.
DOI:10.1890/14-0661.1
|
Jones R C, Kelso D P, Schaeffer E. 2008. Spatial and seasonal patterns in water quality in an embayment-mainstem reach of the tidal freshwater Potomac River, USA: a multiyear study[J]. Environmental Monitoring and Assessment, 147: 351–375.
DOI:10.1007/s10661-007-0126-0
|
Kerman J, Gelman A. 2007. Manipulating and summarizing posterior simulations using random variable objects[J]. Statistics and Computing, 17: 235–244.
DOI:10.1007/s11222-007-9020-4
|
Khuri A I, Sahai H. 1985. Variance Components Analysis: A Selective Literature Survey[J]. International Statistical Review, 53: 279–300.
DOI:10.2307/1402893
|
李文赞, 李叙勇, 王晓学. 2013. 20年来密云水库主要入库河流总氮变化趋势和影响因素[J]. 环境科学学报, 2013, 33(11): 3047–3052.
|
梁中耀, 刘永, 盛虎, 等. 2014. 滇池水质时间序列变化趋势识别及特征分析[J]. 环境科学学报, 2014, 34(3): 754–762.
|
梁中耀, 张雨宇, 钱松, 等. 2017. 基于二项分布检验法的水质达标评价方法研究[J]. 环境科学学报, 2017, 37(1): 339–346.
|
Monnahan C C, Thorson J T, Branch T A. 2017. Faster estimation of Bayesian models in ecology using Hamiltonian Monte Carlo[J]. Methods in Ecology & Evolution, 8(3): 339–348.
|
茆诗松, 汤银才. 2012. 贝叶斯统计(第2版)[M]. 北京: 中国统计出版社: 237–238.
|
Nakagawa S, Schielzeth H. 2012. The mean strikes back: mean-variance relationships and heteroscedasticity[J]. Trends in Ecology & Evolution, 27(9): 474–475.
|
Neuenschwander B, Wandel S, Roychoudhury S, et al. 2015. Robust exchangeability designs for early phase clinical trials with multiple strata[J]. Pharmaceutical Statistics, 15(2): 123–134.
|
Oldenkamp R, Hendriks H W M, MeentD V D, et al. 2015. Hierarchical bayesian approach to reduce uncertainty in the aquatic effect assessment of realistic chemical mixtures[J]. Environmental Science & Technology, 49(17): 10457–10465.
|
Qian S S, Chaffin J D, DuFour M R, et al. 2015a. Quantifying and reducing uncertainty in estimated microcystin concentrations from the ELISA method[J]. Environmental Science & Technology, 49(24): 14221–14229.
|
Qian S S, Craig J K, Baustian M M, et al. 2009. A bayesian hierarchical modeling approach for analyzing observational data from marine ecological studies[J]. Marine Pollution Bulletin, 58(12): 1916–1921.
DOI:10.1016/j.marpolbul.2009.09.029
|
Qian S S, Cuffney T F, Alameddine I, et al. 2010. On the application of multilevel modeling in environmental and ecological studies[J]. Ecology, 91(2): 355–361.
DOI:10.1890/09-1043.1
|
Qian S S, Shen Z. 2007. Ecological applications of multilevel analysis of variance[J]. Ecology, 88(10): 2489–2495.
DOI:10.1890/06-2041.1
|
Qian S S, Stow C A, Cha Y. 2015b. Implications of stein's paradox for environmental standard compliance assessment[J]. Environmental Science & Technology, 49(10): 5913–5920.
|
Qian S S. 2015. The frequency component of water quality criterion compliance assessment should be data driven[J]. Environmental Management, 56(1): 24–33.
DOI:10.1007/s00267-015-0493-1
|
Schielzeth H, Nakagawa S. 2013. Nested by design: model fitting and interpretation in a mixed model era[J]. Methods in Ecology & Evolution, 4(1): 14–24.
|
Sharpley A, Jarvie H P, Buda A, et al. 2013. Phosphorus legacy: overcoming the effects of past management practices to mitigate future water quality impairment[J]. Journal of Environmental Quality, 42(5): 1308–1326.
DOI:10.2134/jeq2013.03.0098
|
Smith A N H, Anderson M J, Millar R B. 2012. Incorporating the intraspecific occupancy-abundance relationship into zero-inflated models[J]. Ecology, 93(12): 2526–2532.
DOI:10.1890/12-0460.1
|
Smith E P, Zahran A, Mahmoud M, et al. 2003. Evaluation of water quality using acceptance sampling by variables[J]. Environmetrics, 14(4): 373–386.
DOI:10.1002/(ISSN)1099-095X
|
Stan Development Team. 2016. RStan: the R interface to Stan. [OL] 2017-03-28. http://mc-stan.org/
|
Stein C. 1955. Inadmissibility of the usual estimator for the mean of a multivariate normal distribution[C]. Proceedings of the Third Berkeley Symposium, 1:197-206
|
Tiao G C, Box G E P. 1967. Bayesian analysis of a three-component hierarchical design model[J]. Biometrika, 54(1/2): 109–125.
DOI:10.2307/2333855
|
Touchon J C, McCoy M W. 2016. The mismatch between current statistical practice and doctoral training in ecology[J]. Ecosphere, 7(8): e01394.
DOI:10.1002/ecs2.1394
|
Vehtari A, Gelman A, Gabry J. 2016. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC[J]. Statistics & Computing, 27(5): 1413–1432.
|
Violle C, Enquist B, McGill B, et al. 2012. The return of the variance: intraspecific variability in community ecology[J]. Trends in Ecology & Evolution, 27(4): 244–252.
|
Zhao L, Li Y, Zou R, et al. 2013. A three-dimensional water quality modeling approach for exploring the eutrophication responses to load reduction scenarios in Lake Yilong (China)[J]. Environmental Pollution, 177: 13–21.
DOI:10.1016/j.envpol.2013.01.047
|
周丰, 郭怀成, 刘永, 等. 2007. 基于多元统计分析和RBFNNs的水质评价方法[J]. 环境科学学报, 2007, 27(5): 846–853.
|
 2017, Vol. 37
2017, Vol. 37


