2. 东北财经大学博士后科研流动站, 大连 116025
2. Postdoctoral Research Station, Dongbei University of Finance and Economics, Dalian 116025
近年来, 随着中国在全球经济体系中的地位愈加重要、能源消耗量和温室气体排放量更是迅速增长.为了积极应对全球气候变化, 推动世界各国切实采取措施降低二氧化碳排放, 2014年11月12日, 中国政府与美国政府在北京联合发表了《气候变化联合声明》(环球网, 2015), 声明提出:“中国计划2030年左右二氧化碳排放达到峰值且将努力早日达峰, 并计划到2030年非化石能源占一次能源消费比重提高到20%左右.”落实2030年二氧化碳排放峰值目标, 要求我国二氧化碳排放管理从强度控制逐步向总量控制过渡, 而科学合理的碳排放总量区域分解是实施碳总量控制的重要支撑.
目前, 减排目标的区域分解研究是国内外学术界关注的重点内容, 相关研究既可以基于不同减排目标的区域分解进行分类, 也可以基于不同分解范围的区域分解进行分类.首先, 基于不同减排目标的区域研究大体可以分为3个类别:①基于绝对减排量的区域分解.绝对减排量是《京都协议书》附件一国家碳减排目标的分配对象, 也是国际上温室气体减排目标区域分配的分解对象(Phylipsen et al., 1998).②基于碳强度减排目标的区域分解.自从中国在2009年提出2020年相比2005年碳排放强度下降40%~45%的减排目标后, 国内外学者纷纷将此目标作为区域分解的减排对象, 根据各省区的地方特色分别制定了它们各自的碳强度减排目标和分担率(Yi et al., 2011).③碳排放强度约束下, 碳排放增量的区域分解.强度减排实质上是CO2排放总量控制的一种“软性”约束.这种约束与总量绝对减排的差别是:在控制期间的一定期段内排放总量继续上升, 因此控制的关键是对增量和增速的控制.中国现阶段碳减排目标的区域分解绝大多数是强度约束下排放总量增量的区域分解.第二, 基于不同分解范围的减排目标区域分解可以分为全球范围不同国家间分解、国家内部不同省区间分解、省区内部的进一步分解等.
总体来看, 国内外关于二氧化碳排放区域分解研究还存在以下不足:①指标选取的单一性和不全面性.目前大多数文献在选取二氧化碳排放分配指标时多以人口指标、人均二氧化碳排放指标等为主, 没有对考虑区域的减排能力和减排的经济代价, 因此建立的指标体系往往过于简单, 这将会导致在数据质量较低或数据缺失时对分配结果产生较大的影响;②区域分解的方法体系中存在较大的主观性, 目前常用的区域聚类、权重指数及关键参数设定等方面的人为影响因素过多.
基于已有研究现状, 本文从效率视角出发, 首次利用零和收益DEA模型进行二氧化碳排放峰值的区域分解研究.零和收益DEA模型是Lins和Gomes等(2003)将博弈论思想与DEA模型相结合所提出的一种优化的DEA模型, 该方法假设任何决策单元(DMU, Decision Making Unit)为达到效率前沿面而增加产出(或减少投入)都将导致其他部分或全部DMU相应地减少产出(或增加投入)以维持投入或产出总量的固定, 进而导致投入或产出量在所有DMU之间进行重新分配并改变原效率前沿面的位置(Lins et al., 2003).ZSG-DEA模型的优点是其能够很好地反映受控资源通过效率竞争方式进行配置的思想, 是一种受到广泛认可的资源配置方法, 因此, 在在控制排放物总量前提下多个决策单元分配效率的评估研究中得到了广泛的应用, 如:不同国家间碳排放权分配(Gomes et al. 2008、Singh et al., 2014、Chiu et al., 2013)、中国不同省区减排责任的分配(郑立群, 2012; Miao et al., 2015); 李小胜等, 2015)及经济分析领域(Hu et al., 2010)等.
本文首次将零和收益DEA模型应用于中国2030年二氧化碳排放峰值区域分解, 现实意义在于从全局考虑, 既能满足中国2030年二氧化碳排放总体达峰要求, 也能使各省区结合自身发展情况实现二氧化碳排放峰值的合理分摊.基于零和收益DEA进行中国二氧化碳排放峰值区域分解与以往关于二氧化碳排放区域分解的区别体现在, 全国二氧化碳排放峰值的地区分解属于在总量一定前提下多个决策单元的分配问题, 一个省区二氧化碳排放的增加必然意味着其他省区二氧化碳排放的减少, 满足“零和逻辑”.各省区可以通过交易使其所增加的碳排放量等于其他省区减少的碳排放量, 从而形成意愿交易矩阵, 达到公平有效的碳交易, 这是与以往对中国二氧化碳排放峰值省区分解研究的主要不同.本文在“零和逻辑”下对中国二氧化碳排放峰值进行省区分配的思路是:第一, 对中国2030年二氧化碳排放峰值总量进行预测, 并根据各省区的历史排放量进行二氧化碳排放峰值的初始省区分解;第二, 利用传统的DEA-BCC模型对各省区的初始分解方案进行效率评估;第三, 基于各省区均达到效率最优的目的, 利用零和收益DEA模型对各省区的初始分解方案进行优化, 最终得到最优的二氧化碳排放峰值省区分解方案.
本文以下各部分内容安排如下:第二部分构建了中国2030年二氧化碳排放峰值的省区分解模型;第三部分对中国2030年二氧化碳排放峰值省区分解的初始结果进行效率评价;第四部分基于零和收益DEA模型对优化的省区分解结果进行分析;第五部分是本文的结论和建议.
2 中国2030年二氧化碳排放峰值省区分解模型的构建(Construction of decomposition model of China′s carbon dioxide emissions peak in 2030) 2.1 中国2030年二氧化碳排放峰值的确定及省区分解的初始方案尽管中国明确提出要在2030年实现二氧化碳排放达峰, 但并没有给出2030年二氧化碳排放峰值的具体目标, 不同研究的预测结果也存在较大差异.本文以2015年公布的中国国家自主贡献预案《强化应对气候变化行动——中国国家自主贡献》(国家发展改革委, 2015)中提出的中国确立的能源绿色低碳发展目标为依据, 对中国2030年二氧化碳排放峰值进行预测, 并对预测峰值进行初始的省区分配.本文预测2030年中国二氧化碳排放峰值及各省区的初始分解共分为5个步骤, 如表 1所示.
| 表 1 中国2030年碳排放峰值预测及初始省区分配方案的分解过程 Table 1 China′s 2030 carbon emission peak forecast and the initial provincial program allocation process |
需要说明的是, 表 1第2步各省区能源消耗量的计算中, 能源类型包括原煤, 焦炭, 原油, 汽油, 煤油, 柴油, 燃料油, 天然气共8大一次化石能源, 并未考虑电力等二次能源消耗.
2.2 中国二氧化碳排放峰值初始省区分解方案的效率评价——DEA-BCC模型二氧化碳排放峰值初始省区分解方案的效率评价基于DEA-BCC模型.该模型有30个相同类型的决策单元(记为DMU, 即30个省区).每个省区的二氧化碳排放量作为模型唯一的投入变量, 各省区人口、能源耗费和地区GDP指标作为模型的产出变量.基于DEA-BCC模型的中国30省区二氧化碳排放区域分解方案的效率评价模型如公式(1)所示:
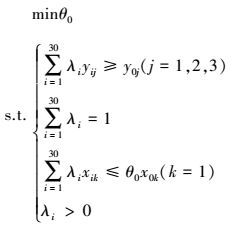
|
(1) |
式中, θ0为目标省区的相对效率, λi为相对于目标省区重新构造一个DMU有效组合中其他省区的组合比例, yij为各省区不同产出变量的大小, 其中i为决策单元(省区), j为产出变量的类型, y0j为目标省区各产出变量的值, k为二氧化碳排放量(即投入变量), 产出变量与投入变量相互独立.x0k为DMU0的初始碳排放配额, xik为第i个省区的二氧化碳排放量分配额.任何一个省区的二氧化碳排放分配达到100%的效率存在两种情况:首先, 在现有的二氧化碳排放总量固定的条件下, 任何一种输出(GDP, 人口, 能源消耗量)都无法增加, 除非同时降低其他种类的输出;其次, 要达到现有的输出, 二氧化碳总量无法降低, 除非同时增加其他种类的输入.
2.3 中国二氧化碳排放峰值省区分解方案的优化——零和收益DEA模型DEA-BCC模型是假设投入或产出变量之间是完全独立的, 即给定任意的一个省区, 其投入或产出不会影响其他省区的投入或产出, 但如果要求某项投入或产出是固定总量, 这种假定便不再成立.此时需要各个省区间的投入或产出相互关联, 从而保证总量不变.也就是说, 如果一个省区为了达到边际有效而增加其投入或产出, 则其他省区必须要减少其投入或产出以保持固定总量不变.这种情况与零和博弈十分相似, 参与博弈的各方在严格竞争下, 一方收益必然意味着另一方损失, 博弈各方的收益和损失相加总和永远为“零”, 双方不存在共赢的可能.这种情况下, 传统DEA模型仅能给出初始状态的相对效率, 不能满足投入总量固定的要求.针对DEA-BCC模型的不足, Lins和Gomes提出了零和收益DEA模型, 该模型通过对投入或产出的再配置, 从而可以根据决策单元的DEA效率值对非期望产出的分配方案进行调整.
在投入导向零和收益DEA模型中, 设目标省区为非DEA有效的决策单元DMU0, 其为了达到DEA有效就必须减少对投入(二氧化碳排放量)的使用, 那么目标省区用于给其他省区分配的二氧化碳排放减少量为:

|
(2) |
式中, x0为DMU0的初始二氧化碳排放配额, v为DMU0的二氧化碳排放减少量, δ0为DMU0的零和收益DEA分配效率值.投入减少量v将按照一定比例分配给其他29个省区, 第i个省区(DMUi)从目标省区(DMU0)处得到的二氧化碳排放量分配调整额度为:
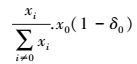
|
(3) |
由于所有省区都在进行投入的比例消减, 所以最终投入量(二氧化碳排放量)对决策单元DMUi(i省区)的再分配额x′i为:
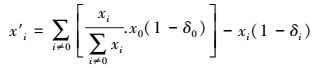
|
(4) |
经过比例调整后, 零和收益DEA模型对DMU0(目标省区)的相对效率评价的投入导向BCC模型转化为公式(5)所示:
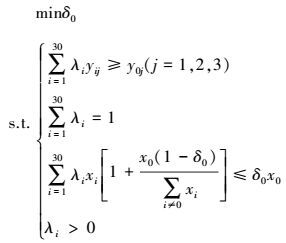
|
(5) |
根据公式(4)进行初始二氧化碳排放分配, 可以得到各个省区间的意愿交易矩阵.由于所有为达到分配效率DEA有效的决策单元DMU(各省区)都会按照比例向其他DMU分配多余投入, 所以有可能出现某些DMU即使完成了多余投入的削减也无法实现DEA有效, 因此本文选择采用多次迭代法来处理这个问题.该方法可以通过多次迭代的方式对投入(二氧化碳排放量)进行多次再分配, 从而使每个DMU都达到DEA有效边界, 此时的分配结果便可以作为较为理想的省区间二氧化碳排放分配方案.
图 1为比例消减策略下的零和收益DEA模型的有效边界.图 1中, DWU0为具体的决策单元, x0为DMU0的初始二氧化碳排放配额, v为DMU0的二氧化碳排放减少量, θ0x0, δ0x0分别为DEA-BCC模型和零和收益DEA模型下目标省区的分配额.从图 1可知, 零和收益DEA效率值优于传统的DEA-BCC效率值.
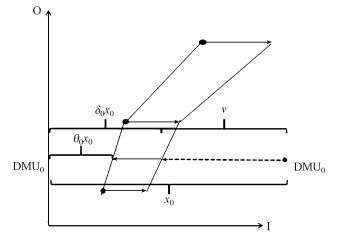 |
| 图 1 比例消减策略下的零和收益DEA模型的有效边界示意图 Fig. 1 The effective boundary of the zero sum gains DEA model under proportional reduction strategy |
根据2.1节的初始省区分解方法, 中国2030年二氧化碳排放峰值省区分解的初始结果及利用DEA-BCC模型计算出的综合效率值如表 2所示.
| 表 2 中国2030年二氧化碳排放峰值省区分解的初始方案及效率值 Table 2 The initial provincial decomposition of carbon dioxide emissions peak in China in 2030 and efficiency |
由表 2各省区初始分解的二氧化碳排放峰值配额可知:分配到最多初始二氧化碳排放峰值的省区是山东省, 达到了325176.79万t, 其二氧化碳排放峰值配额占总二氧化碳排放量的9.77%, 其次是河北省, 二氧化碳排放峰值比重为7.57%, 有5个省区的二氧化碳排放峰值比重达到了6%以上, 属于分配到较多初始二氧化碳排放峰值的省区;而甘肃、天津、广西等9个省区的二氧化碳排放峰值比重普遍偏小(2%以下), 其中青海省最小, 只有14051.37万t, 占二氧化碳排放总量的0.42%.由于初始碳排放权配额是将2030年的全国碳排放峰值按照各省2005—2014年历史累计碳排放量占全国总量的比重为依据分配的, 因此导致过去排放量越多的省区反而在峰值约束下分配到了较多的碳排放权配额, 没有做到应有的减排责任和达峰贡献, 因此, 这些二氧化碳排放峰值比重和经济规模均比较大的省区在分配效率上的表现并不理想, 除江苏省以外, 辽宁、山西、河北和山东省的DEA效率值均明显低于平均水平, 说明这些省区的二氧化碳排放峰值配额需要做进一步调整.
由表 2各省区初次分配的DEA综合效率值可知:①中国二氧化碳排放峰值省区分解的平均效率有待提高.省区分解的初始分配效率平均值为0.63, 说明中国2030年二氧化碳排放峰值的初始省区分解的平均效率处于中等偏上水平, 但仍没有实现全部省区的DEA有效, 且各个省区的分配效率值差异较大.②仅有北京和广西的效率值达到了DEA有效.北京由于各方面发展比较成熟, 因此DEA模型从经济效益产出角度考虑, 更倾向于使北京这种高效减排的省区优先实现DEA有效, 而广西省由于有着良好的区位优势, 各个产业得到了协调发展, 产业结构的重型化趋势显著下降, 因此在初始分配时也达到了有效边界;③少量省区在初始分配中的效率值大于平均效率, 尤其是广东、重庆等4个省区的效率值达到了0.9以上, 这些省市距离有效边界较近, 但仍然尚未达到DEA有效.这些省区的初始效率值较高, 说明在考虑人口经济、能源3个产出因素时, 二氧化碳排放量的分配方式较合理, 能较好地达到有效的二氧化碳排放量, 同时这些省份大多分布于我国中东部地区, 经济发展比较稳定, 第二产业占比较小, 相比北方地区的碳排量与经济发展较适应, 因此效率值较高, 在短期内调整即可实现DEA有效;④部分省区的初始效率值偏低(不到0.4), 距离DEA有效较远.其中宁夏回族自治区的DEA效率值最小, 为0.176.从这些省市的发展现状来看, 大部分属于污染物排放严重的欠发达省区, 经济发展方式单一且粗犷, 产业结构急需调整, 经济与环境未能实现协调统一, 因此这些省区初始二氧化碳排放峰值分配效率较低, 在现阶段经济发展模式下较难实现有效的二氧化碳排放峰值最优分配.
4 中国2030年二氧化碳排放峰值省区分解的优化(Optimization of China′s carbon dioxide emissions peak in 2030)以上分析显示, 中国2030年二氧化碳排放峰值省区分解的初始结果并不理想, 绝大部分省区的分配效率都处于无效状态, 因此本文选择投入导向的零和收益DEA模型对初始分解结果进行多阶段调整, 力求使全部30个省区的综合分解效率达到有效边界.根据2.3节介绍的零和收益DEA模型, 得到各省区二氧化碳排放权调整意愿矩阵, 并进一步计算出调整后的各省区二氧化碳排放权配额, 调整过程中保证投入变量(碳排放总量)保持不变.
4.1 优化的二氧化碳排放峰值省区分解效率经过三轮迭代后, 各省区零和收益DEA模型的综合效率值全部达到1, 实现了DEA有效.各调整阶段中, 30个省区二氧化碳排放权配额的效率评估结果如表 2所示.将表 2零和收益DEA初始效率值与传统DEA-BCC模型的效率值进行比较发现, 所有省区的零和收益DEA模型初始效率值均高于传统DEA模型, 且每一轮调整后的零和收益DEA效率值均比前一阶段的要高, 平均综合效率由初始的0.856最终提升至1, 30个省区的分配效率全部实现了DEA有效.
4.2 优化的二氧化碳排放峰值省区分解方案利用零和收益DEA模型对中国2030年二氧化碳排放峰值进行省区分解的迭代调整后, 最终确定了能够实现最优效率的二氧化碳排放峰值分配方案, 如表 3所示.与初始分解方案相比, 优化后的各省区分解方案变动较大, 具体变动方向和数额如表 3倒数第2列的“调整方式”所示.由于全国的峰值目标是固定不变的, 所以在零和收益DEA模型对全国2030年的碳排放峰值总量的地区分配方案进行优化调整时, 必然出现一些省份碳排放权配额上升的同时另一些省份随之下降的现象.具体来看, 需要减少二氧化碳排放峰值配额的省区共8个, 分别是内蒙古、黑龙江、安徽、山东、新疆等省区, 而其余12个省区则可以增加其配额.其中, 内蒙古需要减少的二氧化碳排放配额最多, 高达137112.41万t;山西省是增加配额最多的省区, 可以增加63891.74万t, 同时也是最终分配方案中二氧化碳排放配额最多的省份, 达到了285263.49万t, 占2030年全国碳排放峰值总量的8.569%;而最终二氧化碳排放配额最少的是青海省, 在削减了4237.86万t配额后只剩下9813.51万t最终二氧化碳排放峰值, 占2030年全国碳排放峰值总量的0.295%.
| 表 3 中国2030年二氧化碳排放峰值的省区优化分解及效率值 Table 3 The optimal provincial decomposition and efficiency values of carbon emissions peak in China in 2030 |
按照各省区在最终二氧化碳排放峰值分配方案中的配额占比大小, 本文将中国30个省区划分为5个类别, 第1类是最终二氧化碳排放配额占总配额比重2%以下的7个省区;第2类是配额占比在2%~3%的8个省区;第3类为配额占比在3%~5%的9个省区;第4类是配额占比在5%~7%的3个省区;第5类为配额占比在7%以上的3个省区.各省区在最终分配方案下的二氧化碳排放峰值分配情况如图 2所示.
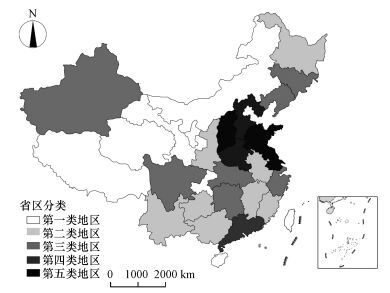 |
| 图 2 中国2030年二氧化碳排放峰值最终省区分解方案 (注:图 2仅为中国大陆省区的调整情况展示, 其中西藏为缺失数据省份.) Fig. 2 The final provincial decomposition scheme for carbon dioxide emissions peak of China in 2030 |
结合表 3中“最终调整的二氧化碳排放配额”列和图 2的数据地图中可以得出以下结论:
① 最终二氧化碳排放权占比较小的地区可以分为两类, 一类是经济较发达地区(如北京、重庆), 另一类则是最不发达的西部地区(如宁夏、青海省等).从第一类地区的经济分布上可以看出, 两种发展水平较极端的地区均分配到了较少的二氧化碳排放配额, 出现这种情况的主要原因是:相比中西部等欠发达地区来说, 较发达地区各方面的发展都比较迅速, 产业结构和能源消耗结构也已经有了一定程度的调整和优化, 且经济产出能力较强, 因此在减排效率方面表现出众, 有足够能力在比较有限的二氧化碳排放约束下照旧完成经济目标, 由于待分配的全国碳排放峰值约束不变, 因此零和收益DEA模型会在分配调整过程中向其他减排效率较低而减排潜力较高的地区转移, 从而保证全国各省份都能在有限的碳排放权配额内完成减排任务和达峰目标.由此, 为了不影响省内经济发展和全国达峰目标的实现, 这些地区应借助西部开发等国家战略的帮助重点发展高能效、低污染、高产出产业, 对于东部地区高污染、低产出、高能耗产业的转移要尽量避免, 有选择性地优先接收技术先进产业的转移.同时, 发挥西部地区的地理优势, 大力推动风电与太阳能等可再生能源的开发利用, 争取做清洁能源的输出大省, 这样不仅有利于拉动地区经济发展, 降低地区碳排放规模, 更有助于将地区碳排放量控制在其本身的碳排放权配额内, 从而为保证全国2030年的碳排放达峰做出有效贡献.
② 最终二氧化碳排放权占比较多的地区基本上属于二氧化碳排放严重但减排潜力较大的省区.第四、五类地区是最终二氧化碳排放权配额占全国峰值总量的比重在5%以上的省区, 分别是河北省、河南省、山东省、山西省等6个省区, 这些省区大部分都具有二氧化碳排放规模较大且减排潜力突出的二氧化碳排放特征.具体来看:河南、山东等省区是传统的能源消耗大省, 能源密集型产业的总产值占地区总产值的比重过高.同时, 由于经济的不发达和减排技术的落后, 导致其能源消费效率(单位增加值能耗)又远高于其他省区.因此这两个省区减排潜力的挖掘重点应放在能源结构优化和减排技术升级方面, 加快新能源基础设施的建设和推广, 同时借鉴发达地区的高科技减排技术手段, 从而在不影响生产和需求规模的情况下降低省区二氧化碳排放量, 目的是保证本地的碳排放规模不超过其在峰值约束下分配到的碳排放权配额;山西省是中国的能源输出大省, 长期依靠开发和出口煤炭等传统能源的方式支撑地区经济发展.为了响应国家节能减排和达峰计划的号召, 山西省应努力改变其粗放型的发展模式, 积极引进国外先进低碳技术和能源开采技术, 大力推动太阳能、风能等清洁能源的开发和利用, 充分发挥其在能源结构“绿色化”转型方面的潜力优势, 为其他省区的能源转型工作做出表率.
③ 最终二氧化碳排放配额占比居中的第二、三类省区应根据自身实际情况尽快制定适合自己的节能减排策略, 力求在有限的二氧化碳排放配额内保证地区经济规模的平稳发展.如辽宁和黑龙江等东北老工业基地省区的第二产业比重较高, 其产业结构的重型化给减排工作和达峰目标的实现带来一定难度, 因此应加大对高新技术产业和服务业的开发和建设, 从而促进地区经济发展方式的低碳转型, 逐渐由粗放型向集约型方向转变.
4.3 比较与讨论目前, 对碳排放目标进行区域分解研究时, 综合指数法、情景分析法和ELC模型等是常用的几种方法.与利用综合指数法和情景分析法的研究相比, 本文利用零和收益DEA模型对二氧化碳峰值目标进行省区分解能够有效排除主观因素的影响, 将2030年二氧化碳峰值按照客观效率值合理分摊至各省区, 使分配结果更具科学性;与ELC模型相比, 本文不仅考虑了经济因素对二氧化碳排放量减排效率的影响, 还考虑了能源消耗量和人口因素对二氧化碳减排量的影响, 充分兼顾了不同省区在能源、经济、人口等方面的差异性.
与以往利用零和收益DEA模型进行地区碳排放权分配的研究相比, 本文首次将零和收益DEA模型应用于碳排放峰值目标的分解研究中, 而碳排放峰值目标的分解满足零和收益DEA模型背后的“零和逻辑”, 使本文的研究更具现实意义;同时, 本文对碳排放峰值的初始省区分配结果基于传统DEA模型的进行效率评价, 重点结合效率值较高和偏低省区的发展现状进行讨论, 为零和收益DEA模型的后续应用提供基础;此外, 在最终碳排放权分配方案中, 将各省区在最终二氧化碳排放峰值分配方案中的占比分为5个类别, 对各省区从产业结构, 经济政策等方面进行了详细剖析, 为碳排放峰值目标的分配政策制定提供了理论与现实相结合的依据.
5 结论(Conclusions)1) 对各省区二氧化碳排放峰值初始分解结果进行效率评估时发现, 各省区间的DEA效率值存在较大差异, 较发达地区更容易达到有效边界, 且初始配额较大省区的DEA效率值往往偏低.
2) 由最终的碳排放峰值分解方案可以看出, 由于待分配的全国2030年碳排放峰值约束不变, 同时为了保证全国各省份都能在有限的碳排放权配额内完成减排任务和达峰目标, 零和收益DEA模型在分配调整过程中将更多的碳排放配额向减排效率较低而减排潜力较高的地区转移.
6 建议(Suggestion)1) 各省区应根据自身实际情况制定切实可行的节能减排策略, 以求在不影响地区经济发展的前提下尽快实现减排任务和二氧化碳达峰目标.各地方政府应客观分析其自身的节能基础和减排潜力, 因地制宜地选择与本地的区域特征和资源禀赋向适应的减排政策, 注意做好经济、减排和环境之间的协调发展.
2) 国家应给予落后地区适当的政策支持, 同时加大区域间交流合作.对于经济相对落后且减排效率较低的地区, 过少的二氧化碳排放配额也许会对其未来的地区经济发展带来阻碍, 导致与其他省区的贫富差距越拉越大, 因此如果要按照最佳效率分配方案进行二氧化碳排放峰值的权利分摊, 那么就需要相关扶持政策和财政转移支付制度做支撑, 同时加强东部等较发达地区与中西部和北部等欠发达地区的交流合作, 从而帮助较落后地区进行低碳技术升级和产业结构优化, 保证各省区在公正原则下平等发展;③利用市场化手段, 加快二氧化碳排放交易市场体系的建立.
Adam Sieminski.2016.International Energy Outlook 2016[R]. Report. Washington: Energy Information Administration:1-35
|
Chiu Y H, Lin J C, Hsc C C, et al. 2013. Carbone mission allowances of efficiency analysis: application of super SBM ZSG-DEA model[J]. Journal of Environment Study, 22(3): 653–666.
|
柴麒敏, 陈怡, 徐华清. 2015. 碳强度和总量双控目标下的区域指标分解方案研究——以温州市为例[J]. 中国能源, 2015, 37(4): 28–32.
|
邓宣凯, 喻艳华, 刘艳芳. 2014. "十二五"各省区CO2排放控制及减排压力评价[J]. 经济地理, 2014, 34(5): 155–161.
|
丁仲礼, 段晓男, 葛全胜, 等. 2009. 国际温室气体减排方案评估及中国长期排放权讨论[J]. 中国科学:地球科学, 2009, 39(12): 1659–1671.
|
Ekholm T, Soimakallio S, Moltmann S, et al. 2010. Effort sharing in ambitious, global climate change mitigation scenarios[J]. Energy Policy, 38(4): 1797–1810.
DOI:10.1016/j.enpol.2009.11.055
|
Gomes E G, Souza G S. 2010. Allocating financial resources for competitive projects using a zero sum gains DEA model[J]. Engevista, 12(1): 4–9.
|
Elzen M D, Höhne N, Moltmann S. 2008. The Triptych approach revisited: A staged sectoral approach for climate mitigation[J]. Energy Policy, 36(3): 1107–1124.
DOI:10.1016/j.enpol.2007.11.026
|
Gomes E G, Lins M P. 2008. Modeling undesirable outputswith zero sum gains data envelopment analysis models[J]. Journal of the Operational Research Society, 59(5): 616–623.
DOI:10.1057/palgrave.jors.2602384
|
Groenenberg H, Phylipsen D, Blok K. 2001. Differentiating commitments world wide: Global differentiation of GHG emissions reductions based on the Triptych approach-a preliminary assessment[J]. Energy Policy, 29(12): 1007–1030.
DOI:10.1016/S0301-4215(01)00027-1
|
国家发展改革委. 2015. 我国提交应对气候变化国家自主贡献文件[OL]. 2015-06-30, http://zys.ndrc.gov.cn/xwfb/201506/t20150630_710182.html
|
国家统计局. 中国能源统计年鉴2015[M]. 北京: 中国统计出版社
|
国家统计局. 2017. 中华人民共和国国家数据[OL]. 2017-04-02, http://data.stats.gov.cn/easyquery.htm?cn=C01
|
IPCC.2006. Guidelines for National Greenhouse Gas Inventories [OL]. 2017-03-15, https://www.transparency-partnership.net/ipcc-2006-guidelines-national-greenhouse-gas-inventories
|
Lins M P E, Gomes E G, João Carlos C B, et al. 2003. Olympic ranking based on a zero sum gains DEA model[J]. European Journal of Operational Research, 148(2): 312–322.
DOI:10.1016/S0377-2217(02)00687-2
|
李小胜, 宋马林. 2015. "十二五"时期我国碳排放额度分配评估及效率研究[J]. 经济科学, 2015, 37(5): 58–69.
|
林文声, 胡新艳. 2014. 广东省碳减排总量目标的地区分解及其盈亏格局[J]. 热带地理, 2014, 34(5): 618–626.
|
刘春兰, 蔡博峰, 陈操操, 等. 2013. 中国碳减排目标的地区分解方法研究述评[J]. 地理科学, 2013, 33(9): 1089–1097.
|
Lu B, Xu Z. 2014. Study on China's energy-saving intensity target decomposition based on zero sum gains DEA model[J]. Wit Transactions on Information & Communication Technologies, 48: 487–494.
|
Miao Z, Geng Y, Sheng J. 2015. Efficient allocation of CO2 emissions in China: a zero sum gains dataenvelopment model[J]. Journal of Cleaner Production, 112: 4144–4150.
|
Phylipsen G, Bode J, Blok K, et al. 1998. A Triptych sectoral approach to burden differentiation; GHG emissions in the European bubble[J]. Energy Policy, 26(12): 929–943.
DOI:10.1016/S0301-4215(98)00036-6
|
Sheng J, Miao Z, Ozturk U A. 2016. A methodology to estimate national REDD+ reference levels using the Zero-Sum-Gains DEA approach[J]. Ecological Indicators, 67: 504–516.
DOI:10.1016/j.ecolind.2016.03.010
|
孙根年, 李静, 魏艳旭. 2011. 环境学习曲线与我国碳减排目标的地区分解[J]. 环境科学研究, 2011, 24(10): 1194–1204.
|
UNDESA. 2015.World Population Prospects: the 2015 Revision[R]. United Nations, New York
|
王金南, 蔡博峰, 曹东, 等. 2011. 中国CO2排放总量控制区域分解方案研究[J]. 环境科学学报, 2011, 31(4): 680–685.
|
王金南, 蔡博峰, 严刚, 等. 2010. 排放强度承诺下的CO2排放总量控制研究[J]. 中国环境科学, 2010, 30(11): 1568–1572.
|
环球网. 2015. 中美气候变化联合声明[OL]. 2015-11-27, http://world.huanqiu.com/hot/2015-11/8061877.html
|
邢璐, 马中, 单葆国. 2013. 欧盟碳减排目标分解方法解读及借鉴[J]. 环境保护, 2013, 41(1): 65–67.
|
熊小平, 康艳兵, 冯升波, 等. 2015. 碳排放总量控制目标区域分解方法研究[J]. 中国能源, 2015(11): 15–19.
DOI:10.3969/j.issn.1003-2355.2015.11.003 |
Yi W J, Zou L L, Guo J, et al. 2011. How can China reach its CO2 intensity reduction targets by 2020? A regional allocation based on equity and development[J]. Energy Policy(39): 2407–2415.
|
于潇, 孙猛. 2015. 中国省际碳排放绩效及2020年减排目标分解[J]. 吉林大学社会科学学报, 2015, 55(1): 57–65.
|
袁永娜, 石敏俊, 李娜, 等. 2012. 碳排放许可的强度分配标准与中国区域经济协调发展——基于30省区CGE模型的分析[J]. 气候变化研究进展, 2012, 8(1): 60–67.
|
郑立群. 2012. 中国各省区碳减排责任分摊——基于零和收益DEA模型的研究[J]. 资源科学, 2012, 34(11): 2087–2096.
|
 2017, Vol. 37
2017, Vol. 37


