2. 中国科学院大学资源与环境学院, 北京 100049;
3. 中国科学院南京地理与湖泊研究所湖泊与环境国家重点实验室, 南京 210008
2. College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049;
3. State Key Laboratory of Lake Science and Environment, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008
太湖流域上游平原河网地区地势较低, 周边工业密集, 流入河网的污染物负荷较大, 河流水质日趋恶化, 水污染已成为影响该地区环境与经济可持续发展的一个主要问题(Duan et al., 2009).确定污染物的削减量是实行污染物总量控制的基础和核心, 同时也是实现太湖流域上游平原河网水质目标管理的主要手段(张利民等, 2009;周笑白等, 2014).污染物在随河流输移的过程中由于物理、化学和生物的综合作用, 浓度会发生衰减, 衰减的速率常数用综合衰减系数表示(Obst, 2003;Wei et al., 2009;游雪静等, 2014).综合衰减系数是计算水环境容量和确定污染物削减量的重要参数, 在区域排污总量控制计划的制定, 总量负荷指标的科学分配以及控制计划执行过程中的管理等工作中发挥着重要作用(寇晓梅, 2005;吴建兰等, 2012).综合衰减系数的测定方法主要有实验室模拟、现场实测和经验公式3种方法, 实验室模拟不能充分模拟现场河流的水动力条件, 测定结果往往低于实际值;现场实测的结果可信度高, 是优先选用的方法, 但需要消耗大量的人力物力;经验公式法是一种简便快捷的方法, 但精度往往不高(慕金波等, 1997;刘中峰等, 2014).朱晓娟等(2013) 采用实测资料反算法测得枯水期松花江干流NH4+-N的综合衰减系数为0.0980~0.1198 d-1.叶常明等(1986) 认为NH4+-N的综合衰减主要是由硝化作用和挥发作用共同引起的, 通过实验室模拟和现场水团追踪测得沱江NH4+-N的综合衰减系数为1.6760 d-1.王雅钰等(2014) 利用模拟河道分别考察了曝气复氧、人工水力循环和渗滤技术对河水中化学需氧量(COD)和NH4+-N综合衰减系数的影响, 实验结果表明3种河道修复措施均可提高COD和NH4+-N的综合衰减系数, 其中以渗滤技术的效果最明显.王晓青(2015) 利用模型对三峡工程蓄水前后澎溪河回水区高锰酸盐指数、NH4+-N和TP的综合衰减系数进行了模拟计算, 蓄水前高锰酸盐指数、NH4+-N和TP的综合衰减系数分别为0.1300~0.2500, 0.1100~0.1800和0.0800~0.1300 d-1;蓄水后的综合衰减系数分别为0.0070~0.0160, 0.0060~0.0150和0.0050~0.0120 d-1.污染物的综合衰减系数受污染物性质、温度、pH、溶解氧等环境因素以及流速、水深等河流水力因素的影响(Wright et al., 1979;Chen et al., 2005;曾勇等, 2010;郭儒等, 2008), 季节性河流需要分不同水期测定污染物的综合衰减系数(张亚丽等, 2015).目前污染物综合衰减系数的现场测定常常以上、下游断面之间的距离除以该段河流的平均流速作为水团的衰减时间, 这无法保证这段时间结束时上游断面取样的水团刚好到达下游取样断面, 进而影响测定结果的准确性.
本研究以太湖流域上游平原河网为研究区域, 开展原位实验测定枯水期高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数, 并用一维稳态水质模型对测定结果的可靠性进行验证.研究结果可为太湖流域上游平原河网有机污染物和营养盐的总量控制与管理提供科学参数.
2 研究区域概况(Study area)太湖是中国的第三大淡水湖, 水面面积2338 km2, 流域面积36500 km2, 流域面积只占全国面积的0.4%, 但流域GDP占全国的11%(Han et al., 2015) .太湖流域上游平原河网地处中纬度地区, 亚热带季风气候特征明显, 春夏之交有明显的“梅雨”期;夏季受热带风暴和台风的影响, 降雨量大, 易发洪水灾害.该地区年平均气温15~17 ℃, 由北到南递增;多年平均降雨量约1100 mm, 其中近60%集中在5-9月.太湖流域上游平原河网河床坡降小, 水流速度慢, 水面船只密集, 是重要的水上运输通道.受上游平原河网地区人类活动加剧的影响, 太湖的水质逐渐恶化, 富营养化的风险显著增加(Guo, 2007).
3 材料与方法(Materials and methods) 3.1 采样点设定采样点一般设置在以下断面:①重要的水质监测断面;②水利工程和人工设施的上、下游断面;③水文、水质情况发生显著变化的断面;④较长河流的上游、中游及下游断面.基于上述原则, 在太湖流域上游平原河网共选取20个点(图 1)作为原位测定综合衰减系数的采样点.
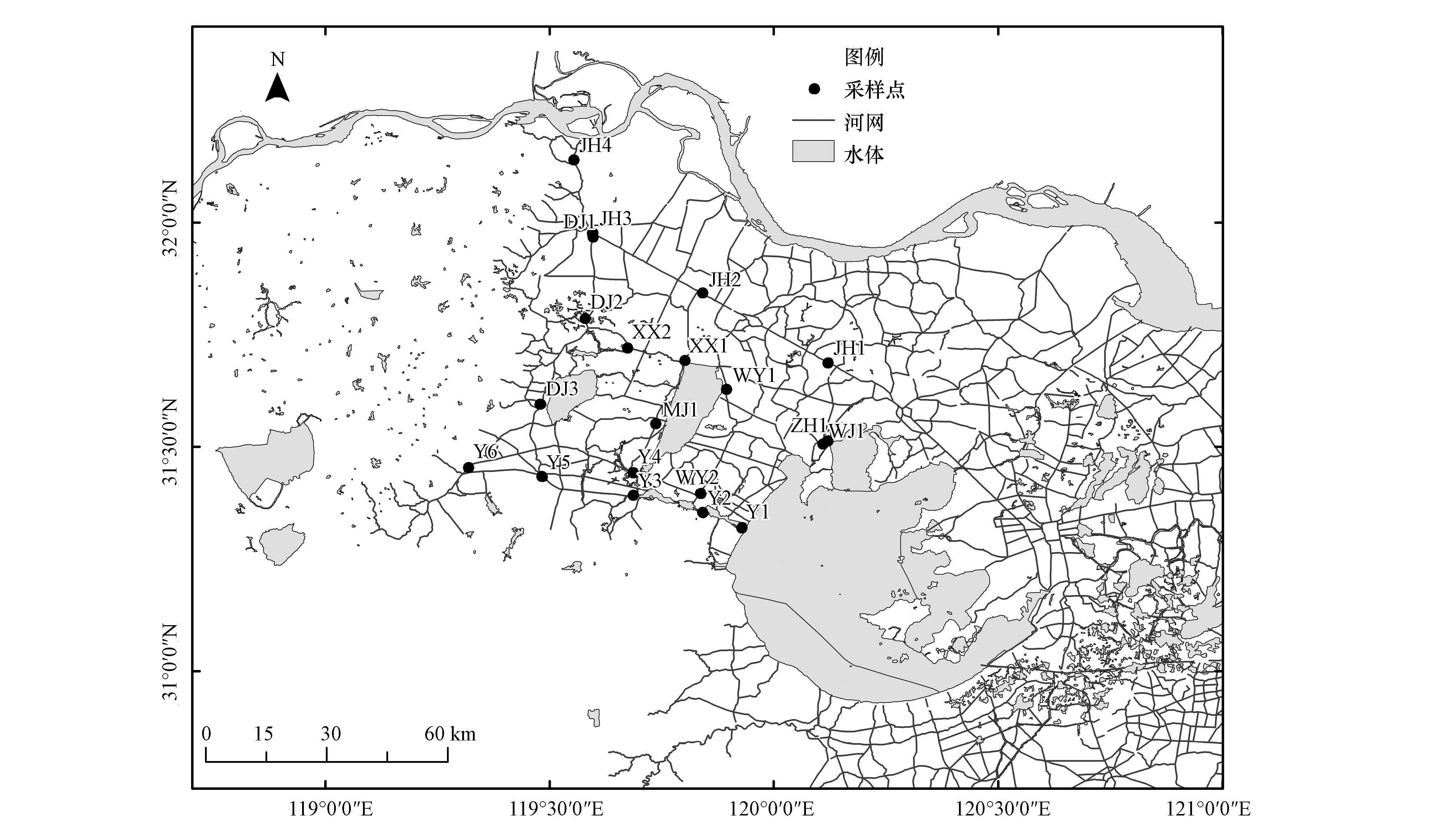 |
| 图 1 采样点位置 Fig. 1 Map of sampling sites |
为开展原位实验, 设计制作了一款玻璃瓶(图 2).玻璃瓶的直径大约90 mm, 高度约150 mm, 体积约700 mL.瓶子的顶部和底部各有一个直径约35 mm的开口, 距底部上方约40 mm处有一直径为8 mm的侧支管.顶部橡胶塞有直径为5 mm的中心孔, 孔中插有玻璃管, 一头通着玻璃瓶内部, 另一头连着约1 m长的橡皮管通向外部大气环境, 底部和侧支管开口配有带橡胶圈的塑料盖.每个采样点由2个玻璃瓶和一个直径约为400 mm的圆形钢架组成.
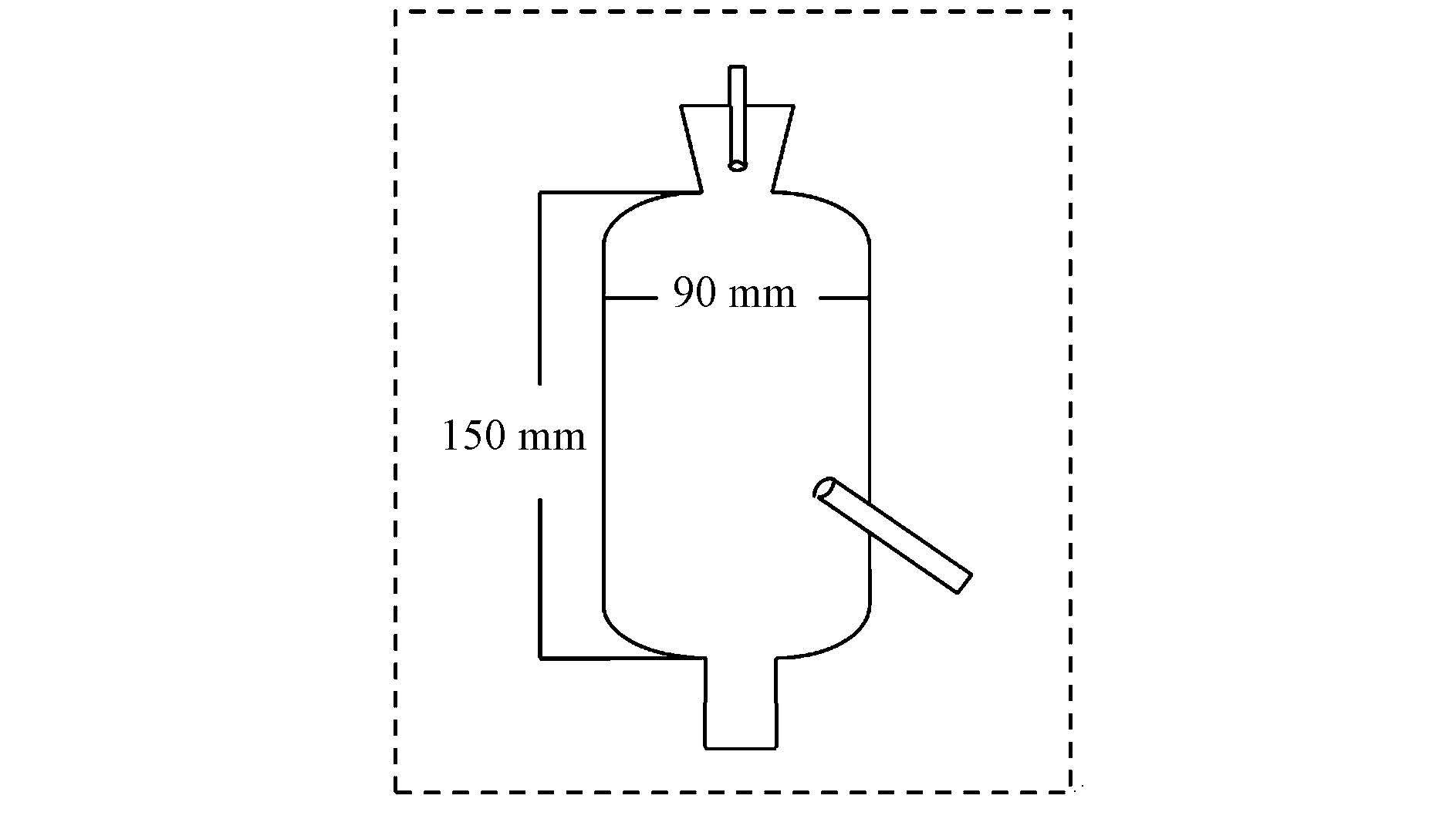 |
| 图 2 实验装置简图 Fig. 2 Diagram of experimental device |
取河流采样断面中心点0.5 m深的水样进行实验, 除了用聚乙烯采样瓶保留一瓶作为综合衰减前的水样外, 2个玻璃瓶装满河水, 盖好橡胶塞后挂在钢架上, 橡皮管的另一端固定在钢架上.最后将整套装置放入取水断面0.5 m水深处固定, 确保橡胶管露出水面能进行气体交换.2 d后, 将玻璃瓶里的上层水从侧支管导入到聚乙烯采样瓶作为综合衰减后的水样.取两个玻璃瓶平行实验结果的均值作为污染物综合衰减系数的最终结果.与实验室模拟实验法相比, 本研究设计的原位实验确保污染物的衰减过程始终处于河流的自然环境中, 减弱了温度、光照、气压以及河流的紊动动能等环境因素对实验结果的影响.
现场使用便携式多参数水质仪测定综合衰减前水样的温度(T)、溶解氧(DO)、pH、氧化还原电位(ORP)、总溶解固体(TDS)和电导率(EC).采用浮标法估算每个采样点的河流流速(u), 用米尺测河流的宽度(B), 并在每个采样断面左、中、右3处测水深并计算平均水深(H).水样加入5 mL 0.1%的氯化汞试剂作为保存药剂(徐少华, 2010), 存放在含冰块的保温箱中, 原位实验结束后迅速送入实验室按照《水与废水监测分析方法(第4版)》(国家环境保护总局, 2006)中的方法确定高锰酸盐指数、NH4+-N、TN和TP的浓度.按照上述实验方法, 2015年12月5日-13日在研究区域20个采样点进行了一次原位实验.
3.3 综合衰减系数计算方法国内外的研究(Wright et al., 1979)表明一级反应动力学能较好地描述污染物的综合衰减过程.本研究根据一级反应动力学方程计算高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数.一级反应动力学方程如下:
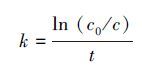
|
(1) |
式中, k为污染物综合衰减系数(d-1), c0为综合衰减前的污染物浓度(mg·L-1), c为综合衰减后的污染物浓度(mg·L-1), t为衰减时间(d).
3.4 综合衰减系数修正方法本研究的原位实验在现场实际温度等环境因素下进行, 由于玻璃瓶被固定于采样断面, 不能模拟河流水力条件对综合衰减系数的影响, 故需要对测定的衰减系数进行水力修正, 修正公式(Wrihgt et al., 1979;王美敬等, 2005)如下:
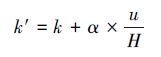
|
(2) |
式中, k′为水力修正后的污染物综合衰减系数(d-1), k为污染物综合衰减系数(d-1), α为河道活度系数, 与河床坡降有关, 本研究统一取0.30(陶威等, 2009), 无量纲, u为河段平均流速(m·s-1), H为河段平均水深(m).
3.5 综合衰减系数的可靠性验证在20个采样点附近选择一段包含采样点在内的河段作为综合衰减系数的验证河段, 要求河道顺直, 无明显支流、排污口和取水口.2015年12月中旬进行现场考察获得了所有河段的基本信息(表 1).
| 表 1 河道基本情况 Table 1 Basic information of watercourses |
由于验证河段无支流、排污口以及取水口等设施且平均深度小于5 m, 可认为污染物在横向和垂向上浓度分布比较均匀, 污染物浓度的变化主要由纵向弥散与平流引起, 故采用一维稳态水质模型对修正前后的综合衰减系数分别进行验证.一维稳态水质模型(不考虑源汇项)的数学方程如下:
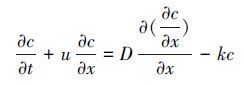
|
(3) |
式中, c为污染物浓度(mg·L-1), t为时间(d), u为平均流速(m·s-1), D为纵向分散系数(m2·s-1), x为距离上游断面的距离(m), k为综合衰减系数(d-1).
纵向分散系数D根据式(4) (Fisher, 1975;蒋忠锦等, 1997)计算:
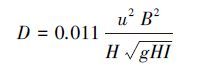
|
(4) |
式中, D为纵向分散系数(m2·s-1), B为河流宽度(m), u为平均流速(m·s-1), H为平均水深(m), g为重力加速度(m·s-2), I为河床坡降(无量纲).
根据一维稳态水质模型可预测下游断面污染物的浓度值c:

|
(5) |
式中, c0为上游断面污染物浓度(mg·L-1), c为下游断面污染物浓度(mg·L-1), u为平均流速(m·s-1), x为距离上游断面的距离(m), D为纵向分散系数(m2·s-1), k为综合衰减系数(d-1).
4 结果(Results) 4.1 物理化学指标现场测定20个采样点综合衰减前水样的T、DO、pH、ORP、TDS和EC共6项物理化学指标的结果见表 2.由表 2可知, 20个采样点水样T的范围为9.3~16.1 ℃, 最高值和最低值对应的采样点分别为Y1点和JH2点;DO的范围为4.8~7.8 mg·L-1, 最高值和最低值对应的采样点分别为Y1、WJ1和WY2;pH的范围为7.55~8.61, 采样点之间的差异较小;ORP的范围为95~208 mV, 最高值和最低值对应的采样点分别为JH2和DJ1;WY2的TDS浓度最高647.8 mg·L-1, 约是JH2最低浓度217.5 mg·L-1的3倍;EC的范围为339.8~662.0 μS·cm-1, 最高值和最低值对应的采样点分别为DJ1和JH2.除pH外, 各采样点之间其余5项指标均表现出较大差异, 表明水质的空间差异较明显.
| 表 2 物理化学指标 Table 2 Physico-chemical indicators of water samples |
根据一级反应动力学方程对20个采样点高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数进行了计算, 结果见表 3.由表 3可知, 高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数范围依次为:0.0296~0.4106、0.0224~0.3564、0.0137~0.3046和0.0555~0.5725 d-1, 平均值分别为0.1496、0.1377、0.1328和0.3219 d-1.高锰酸盐指数、NH4+-N、TN和TP综合衰减系数最大值和最小值对应的采样点依次为:XX1和WY1、DJ1和Y4、Y2和Y4以及JH4和Y4.Y4点NH4+-N、TN和TP的综合衰减系数均为最大, 可能原因是Y4点水深较浅、河道窄、属于小型河流(Alexander et al., 2000).从变异系数(CV)来看, TP综合衰减系数的空间变异性最小(0.4676 < 0.6361 < 0.6452 < 0.6986) , 表明太湖流域上游平原河网各采样点之间TP的自净能力差别较小.
| 表 3 综合衰减系数的计算值 Table 3 Calculating values of integrated degradation coefficients |
根据式(2) 对高锰酸盐指数、NH4+-N、TN和TP综合衰减系数的计算值进行水力修正, 得到综合衰减系数的修正值(表 4).经过水力修正, 4种水质指标的综合衰减系数均增大.高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数范围分别为:0.0354~0.4144、0.0265~0.3616、0.0175~0.3098和0.0581~0.5777 d-1, 平均值依次为0.1542、0.1430、0.1380和0.3271 d-1.修正后高锰酸盐指数、NH4+-N、TN和TP综合衰减系数最大值和最小值对应的采样点没有变化, 综合衰减系数CV值的大小顺序也与修正前相同.
| 表 4 综合衰减系数的修正值 Table 4 Adjusted values of integrated attenuation coefficients |
根据每段验证河段上游断面水质指标的浓度, 利用式(5) 预测下游断面的预测浓度, 通过预测值与实测值的相对误差(RE)验证修正前后综合衰减系数的可靠性.RE的计算方法如下:

|
(6) |
式中, RE为相对误差(%).
4.4.1 综合衰减系数的可靠性验证高锰酸盐指数、NH4+-N、TN和TP综合衰减系数的验证结果见表 5.高锰酸盐指数的RE变化范围为0.49%~22.04%, 除了WY2点外, 其余各点的RE均小于20%, 说明高锰酸盐指数的预测值与实测值基本吻合.NH4+-N 的RE变化范围为4.21%~54.27%, 其中Y4、ZH1、WY1和DJ1的RE超过了20%.TN的 RE变化范围为0.86%~35.65%, 3个采样点(Y3、Y4和XX1) 的RE超过了20%.TP的RE变化范围为4.24%~49.27%, 25%的采样点(Y3、Y4、WY1、WY2和XX1) 的RE超过了20%.以RE的平均值为标准, 4种水质指标相对误差均小于20%, 表明综合衰减系数的验证效果较好.4种水质指标综合衰减系数RE由小到大的顺序为:高锰酸盐指数 < TN < NH4+-N < TP, 表明高锰酸盐指数综合衰减系数的可靠性较好, TP综合衰减系数的可靠性较差.
| 表 5 综合衰减系数的可靠性验证 Table 5 Reliability validation of integrated attenuation coefficients |
高锰酸盐指数、NH4+-N、TN和TP综合衰减系数修正值的可靠性验证结果见表 6.经过水力修正, 高锰酸盐指数的RE变化范围为0.13%~21.95%, 除了WY2外, 其余各点RE均小于20%, 说明高锰酸盐指数的预测值与实测值吻合度较高.NH4+-N 的RE变化范围为0.82%~53.46%, 只有Y4、ZH1、WY1和DJ1的RE超过了20%.TN 的RE变化范围为1.27%~34.21%, 有3个采样点(Y3、Y4和XX1) 的RE超过了20%.TP的RE变化范围为4.03%~49.74%, 25%的采样点(Y3、Y4、WY1、WY2和XX1) 的RE超过了20%.以RE的平均值为标准, 4种水质指标相对误差均小于20%, 表明综合衰减系数修正值的验证效果较好, 4种水质指标综合衰减系数修正值的RE平均值大小顺序与修正前相同.
| 表 6 综合衰减系数修正值的可靠性验证 Table 6 Reliability validation of integrated attenuation coefficients after adjustment |
原有的现场实测法以上、下游断面之间的距离除以该河段平均流速计算上游水团到达下游断面的时间, 河段上、下游断面的水样分别作为衰减前和衰减后的水样, 利用一级反应动力学计算综合衰减系数.由于水团在河流中的运动受到多因素的影响, 尤其是表面船只的影响, 不能保证在计算的时间终点, 上游断面取水样的水团刚好到达下游断面, 给综合衰减系数的测定带来较大误差.本研究的实验方案在河流实际环境条件下进行, 而且能够保证综合衰减前后的水样来自同一水团, 避免了原有方法的缺点.
我国河流COD综合衰减系数的范围为0.0090~0.4700 d-1, NH4+-N的综合衰减系数范围为0.1050~0.3500 d-1(郭儒等, 2008).由表 3可知, 高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数范围分别为:0.0296~0.4106、0.0224~0.3564、0.0137~0.3046和0.0555~0.5725 d-1, 平均值依次为0.1496、0.1377、0.1328和0.3219 d-1.本研究高锰酸盐指数与NH4+-N的综合衰减系数结果符合我国综合衰减系数的范围.张亚丽等(2015) 测得枯水期淮河支流COD、NH4+-N和TP的综合衰减系数分别为:0.0484~0.0947、0.0474~0.0507和0.0990~0.1371 d-1.与淮河支流相比, 太湖流域上游污染物的综合衰减系数较大, 但TP综合衰减系数 > 高锰酸盐指数综合衰减系数 > NH4+-N综合衰减系数的规律与淮河支流相吻合.郭栋鹏等(2009) 根据实验室模拟实验得出黄海南部海水中TN的综合衰减系数为0.0360~0.0530 d-1, 略小于本研究TN的综合衰减系数.
污染物的综合衰减系数受污染物性质、T、pH、DO、污染物初始浓度(c0)以及河流水力条件等因素的影响, 本研究将高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数与T、pH、c0、DO、TDS、H和u进行相关分析, 结果见表 7.
| 表 7 综合衰减系数与影响因素的相关分析结果 Table 7 Results of correlation analysis for integrated attenuation coefficients and influencing factors |
表 7显示, 高锰酸盐指数的综合衰减系数与H有显著的相关性(p < 0.01) , TP的综合衰减系数与u显著相关(p < 0.05) .进一步回归分析得出高锰酸盐指数综合衰减系数与H有显著的回归关系:y=-0.056x+0.325, R2=0.347(p <0.01) , 随着H增加, 高锰酸盐的综合衰减系数减小.降解有机污染物的微生物大多分布在沉积物与上覆水界面, 水深增加, 水体与沉积物之间的作用减弱, 有机污染物的综合衰减系数减小(Alexander et al., 2000).TP的综合衰减系数与u有显著的回归关系:y=6.468x+0.015, R2=0.219(p <0.05) , 可见TP的综合衰减系数随u的增大而增大.u增大能够增强稀释、扩散等物理衰减作用, 从而加快TP的综合衰减速率, 但并不是随着u持续增大, TP的综合衰减系数也会持续增大, 较大的u减少了TP在水体中的停留时间, 降低了TP与微生物的接触反应时间, 不利于综合衰减(Meckenstock et al., 2015).太湖上游平原河网的u处于较低的范围内, TP的综合衰减系数与u呈现显著的正相关关系.由于本实验方案中的玻璃瓶被固定而无法模拟水团在河流中的实际流动情况, 而综合衰减系数由于u和H等水力条件密切相关, 所以, 本研究采用前人总结的经验公式对测定的综合衰减系数进行了水力修正.
本实验设计虽然能够在现实环境中模拟污染物的衰减过程, 但是有限的玻璃瓶体积不能够完全反映水生植物对污染物的自然净化作用, 可能会影响实验结果;另一方面太湖上游平原河网大多是人工改造的航道, 河道中水生植物较少, 因此认为水生植物对本研究综合衰减系数的影响较小.关于太湖流域上游平原河网水生植物对污染物的自然净化作用还有待进一步研究.
5.2 综合衰减系数的可靠性验证利用一维稳态水质模型根据高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数预测下游断面水质指标浓度, 预测值与实测值之间相对误差绝对值的平均值依次为8.39%、14.40%、11.43%和19.22%;根据修正后高锰酸盐指数、NH4+-N、TN和TP综合衰减系数预测下游断面水质指标浓度, 产生的相对误差绝对值的平均值依次为10.65%、14.34%、11.37%和19.24%.经过水力修正, 预测值与实测值之间相对误差绝对值的平均值变化较小, 表明枯水期的水力条件对污染物综合衰减系数的影响较小.以相对误差绝对值的平均值大小为标准(相对误差绝对值的平均值越小, 可靠性越大), 4种水质指标综合衰减系数的可靠性顺序为:高锰酸盐指数 > TN > NH4+-N > TP.尽管4种水质指标相对误差绝对值的平均值均小于20%, 但不同水质指标之间的误差水平存在差异.高锰酸盐指数、TN和NH4+-N的误差水平小于15%, 说明这3种水质指标综合衰减系数的可靠性较强, 可能与它们的衰减过程相关.生物作用在高锰酸盐指数、TN和NH4+-N的衰减中起到重要作用, 而生物作用主导的衰减过程与一级反应动力学吻合较好, 所以本研究利用一级反应动力学计算得出的高锰酸盐指数、TN和NH4+-N的综合衰减系数具有较强的可靠性.TP的综合衰减主要靠吸附、沉降等物理化学过程(Vagnetti et al., 2003) , 这些过程难以用一级反应动力学精确模拟, 可能是造成TP综合衰减系数可靠性较低的主要原因.
将利用综合衰减系数和综合衰减系数修正值计算的下游断面水质指标的预测值与实测值进行相关分析, 结果见表 8.
| 表 8 预测值与实测值的相关分析结果 Table 8 Results of correlation analysis for predictive and measured value |
表 8显示, 预测值与实测值均有显著的相关性, 而且相关系数均大于0.9, 说明本研究获得的高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数是可靠的, 能够反映太湖流域上游平原河网枯水期污染物的综合衰减规律.修正前后每种水质指标的相关系数没有变化, 再次表明枯水期的水力条件对污染物综合衰减系数的影响较小, 同时表明枯水期利用本实验获得的综合衰减系数可以忽略水力修正.
本研究采用原位实验测定了枯水期太湖流域上游平原河网高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数并进行了可靠性验证, 验证结果表明综合衰减系数的结果能够代表枯水期研究区域内污染物的自净规律.太湖流域上游平原河网处于季风气候区, 在丰水期和平水期, 大量的面源污染进入河网从而影响污染物的综合衰减过程, 关于丰水期和平水期高锰酸盐指数、NH4+-N、TN和TP的综合衰减系数还需要进一步研究.
6 结论(Conclusions)1) 枯水期太湖流域上游平原河网高锰酸盐指数、NH4+-N、TN和TP综合衰减系数的范围分别为:0.0296~0.4106、0.0224~0.3564、0.0137~0.3046和0.0555~0.5725 d-1, 平均值依次为0.1496、0.1377、0.1328和0.3219 d-1, 水力校正后, 综合衰减系数的变化较小.
2) 利用一维稳态水质模型对枯水期综合衰减系数的可靠性验证表明高锰酸盐指数、NH4+-N、TN和TP综合衰减系数能够为太湖流域上游平原河网的污染物总量控制管理提供科学参数.
3) 水力校正前后综合衰减系数的可靠性验证表明枯水期河流水力特征对污染物综合衰减系数的影响较小, 枯水期的综合衰减系数可以忽略水力修正.
| [${referVo.labelOrder}] | Alexander R B, Smith R A, Schwarz G E. 2000. Effect of stream channel size on the delivery of nitrogen to the Gulf of Mexico[J]. Nature, 403(6771) : 758–761. DOI:10.1038/35001562 |
| [${referVo.labelOrder}] | Chen Y G, Liu Y, Zhou Q, et al. 2005. Enhanced phosphorus biological removal from wastewater-effect of microorganism acclimatization with different ratios of short-chain fatty acids mixture[J]. Biochemical Engineering Journal, 27(1) : 24–32. DOI:10.1016/j.bej.2005.06.003 |
| [${referVo.labelOrder}] | Duan H T, Ma R H, Xu X F, et al. 2009. Two-Decade Reconstruction of Algal Blooms in China's Lake Taihu[J]. Environmental Science & Technology, 43(10) : 3522–3528. |
| [${referVo.labelOrder}] | Fisher B H. 1975. Discussion of ‘simple method for predicting dispersion in streams’ by R[J]. S McQuivey and T.N Keefer[J].Journal of Environmental Engineering, American Society of Civil Engineering, 101(3) : 453–455. |
| [${referVo.labelOrder}] | Guo L. 2007. Ecology-Doing battle with the green monster of Taihu Lake[J]. Science, 317(5842) : 1166–1166. DOI:10.1126/science.317.5842.1166 |
| [${referVo.labelOrder}] | 国家环保总局. 2006. 水与废水检测分析方法(第4版)[M]. 北京: 中国环境科学出版社. |
| [${referVo.labelOrder}] | 郭儒, 李宇斌, 富国. 2008. 河流中污染物衰减系数影响因素分析[J]. 气象与环境学报, 2008, 24(1) : 56–59. |
| [${referVo.labelOrder}] | 郭栋鹏, 杨契, 徐明德. 2009. 黄海南部海水中TN降解规律的研究[J]. 山西农业大学学报(自然科学版), 2009, 29(2) : 178–181. |
| [${referVo.labelOrder}] | Han T, Zhang H J, Hu W P, et al. 2015. Research on self-purification capacity of Lake Taihu[J]. Environmental Science and Pollution Research, 22(11) : 8201–8215. DOI:10.1007/s11356-014-3920-6 |
| [${referVo.labelOrder}] | 蒋忠锦, 王继徽. 1997. 天然河流一维水质模型的研究与改进[J]. 湖南大学学报(自然科学版), 1997, 24(6) : 91–95. |
| [${referVo.labelOrder}] | 寇晓梅. 2005. 汉江上游有机污染物CODCr综合衰减系数的试验确定[J]. 水资源保护, 2005, 21(5) : 31–33. |
| [${referVo.labelOrder}] | 刘中峰, 曹玲玲, 冯镜洁. 2014. 原型观测法在确定九龙滩水库污染物降解系数中的应用[J]. 水利水电科技进展, 2014, 34(2) : 68–70. |
| [${referVo.labelOrder}] | 慕金波, 酒济明. 1997. 河流中有机物降解系数的室内模拟实验研究[J]. 山东科学, 1997, 10(2) : 52–57. |
| [${referVo.labelOrder}] | Meckenstock R U, Elsner M, Griebler C, et al. 2015. Biodegradation:Updating the Concepts of Control for Microbial Cleanup in Contaminated Aquifers[J]. Environmental Science & Technology, 49(12) : 7073–7081. |
| [${referVo.labelOrder}] | Obst U. 2003. Strategies of maintaining the natural purification potential of rivers and lakes[J]. Environmental Science and Pollution Research, 10(4) : 251–255. DOI:10.1065/espr2003.07.160 |
| [${referVo.labelOrder}] | 陶威, 刘颖, 任怡然. 2009. 长江宜宾段氨氮降解系数的实验室研究[J]. 污染防治技术, 2009, 22(6) : 8–9. |
| [${referVo.labelOrder}] | Vagnetti R, Miana P, Fabris M, et al. 2003. Self-purification ability of a resurgence stream[J]. Chemosphere, 52(10) : 1781–1795. DOI:10.1016/S0045-6535(03)00445-4 |
| [${referVo.labelOrder}] | Wei G L, Yang Z F, Cui B S, et al. 2009. Impact of Dam Construction on Water Quality and Water Self-Purification Capacity of the Lancang River, China[J]. Water Resources Management, 23(9) : 1763–1780. DOI:10.1007/s11269-008-9351-8 |
| [${referVo.labelOrder}] | 吴建兰, 李曦, 陈秀梅. 2012. 实验室率定法测算长江南通段污染物降解系数[J]. 四川环境, 2012, 31(5) : 36–40. |
| [${referVo.labelOrder}] | 王雅钰, 刘成刚, 黄天寅, 等. 2014. 不同处理技术对河流污染物降解系数影响的比较[J]. 环境工程学报, 2014, 8(3) : 917–923. |
| [${referVo.labelOrder}] | 王晓青. 2015. 三峡工程蓄水对澎溪河回水区COD(Mn)、NH3-N和TP综合衰减系数的影响[J]. 安全与环境学报, 2015, 15(1) : 325–329. |
| [${referVo.labelOrder}] | Wright R M, McDonnell A J. 1979. In-stream deoxygenation rate prediction[J]. Journal of the Environmental Engineering Division, American Society of Civil Engineering, 105(2) : 323–335. |
| [${referVo.labelOrder}] | 王美敬, 罗麟, 程香菊, 等. 2005. 紊动对有机物降解影响研究[J]. 武汉大学学报(工学版), 2005, 38(4) : 1–4. |
| [${referVo.labelOrder}] | 徐少华. 2010. 水样的采集与保存的技术方法探析[J]. 科技传播, 2010(18) : 61–62. |
| [${referVo.labelOrder}] | 叶常明, 谢永明, 穆环珍, 等. 1986. 沱江氮污染物转化规律及污染容量[J]. 环境科学学报, 1986, 6(1) : 37–42. |
| [${referVo.labelOrder}] | 游雪静, 张玉珍, 苏玉萍, 等. 2014. 闽江流域水体氨氮降解系数实验模拟研究[J]. 亚热带资源与环境学报, 2014, 9(1) : 61–67. |
| [${referVo.labelOrder}] | 张利民, 刘洋, 孙卫红, 等. 2009. 太湖流域漕桥河小流域水环境容量估算及污染物削减分配[J]. 湖泊科学, 2009, 21(4) : 502–508. |
| [${referVo.labelOrder}] | 周笑白, 张宁红, 张咏, 等. 2014. 太湖水质与水生生物健康的关联性初探[J]. 环境科学, 2014, 35(1) : 271–278. |
| [${referVo.labelOrder}] | 朱晓娟, 沈万斌, 高凯, 等. 2013. 吉林省松花江干流氨氮综合衰减系数分段研究[J]. 科学技术与工程, 2013, 13(10) : 2758–2761. |
| [${referVo.labelOrder}] | 曾勇, 王西琴. 2010. 浙江西苕溪水环境容量模型与参数灵敏度分析[J]. 中国环境科学, 2010, 30(12) : 1627–1632. |
| [${referVo.labelOrder}] | 张亚丽, 申剑, 史淑娟, 等. 2015. 淮河支流污染物综合降解系数动态测算[J]. 中国环境监测, 2015, 31(2) : 64–67. |
 2017, Vol. 37
2017, Vol. 37


