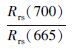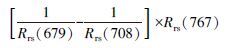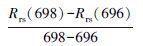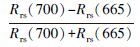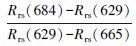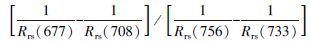2. 无锡市环境监测中心站, 无锡 214121;
3. 合肥市气象局, 合肥 230041;
4. 南京师范大学虚拟地理环境教育部重点实验室, 南京 210023;
5. 江苏省地理信息资源开发与利用协同创新中心, 南京 210023;
6. 南京信息工程大学地理与遥感学院, 南京 210044
2. Wuxi Environmental Monitoring Centre, Wuxi 214121;
3. Hefei Meteorologic Bureau, Hefei 230041;
4. Key Laboratory of Virtual Geographic Environment, Ministry of Education, Nanjing Normal University, Nanjing 210023;
5. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023;
6. School of Geography and Remote Sensing, Nanjing University of Information Science & Technology, Nanjing 210044
叶绿素a浓度(Cchl-a)是衡量水体富营养化和初级生产力的重要参数, 已广泛应用于海洋和内陆水体评价(Honeywill et al., 2002; Lee et al., 2011).遥感监测叶绿素a具有实时、宏观和便于长时间序列监测等优势.目前, 针对一类水体的叶绿素a浓度反演方法较为成熟, 因为较为纯净水体的光学特性主要与浮游植物有关(Huang et al., 2014), 基于蓝绿波段反射率差异等指标进行叶绿素a浓度反演可取得较好效果(Gordon et al., 1983).而沿海和内陆等较为浑浊的二类水体光学特性比较复杂, 其水色要素物质组成受陆源影响较大, 水体中颗粒物的理化性质具有较强的时空差异性, 高浓度、高变异性的非色素颗粒物和有色可溶性有机物(Chromophoric Dissolved Organic Matter, CDOM)的干扰使得建立普适性强、精度高的二类水体叶绿素a浓度反演模型较为困难(黄昌春等, 2013).对于二类水体叶绿素a浓度的光谱反演方法, 已有众多国内外研究人员开展了相关工作.Daniel等(2012) 对二类复杂水体包括叶绿素a在内的主要水色组分算法进行了综述.EL-Alem等(2012) 将APPEL模型(APProach by Elimination), 结合MODIS数据与地面同步实测数据, 应用于南魁北克4个湖泊的叶绿素a浓度反演, 得到了较高的反演精度.Hoogenboom等(1998) 利用AVRIS遥感影像, 以Ljsselneer湖为研究区, 得出估测叶绿素a浓度效果最好的模型为R708/R676.安如等(2013) 在太湖和巢湖中使用归一化叶绿素指数(NDCI)建立了叶绿素a的反演模型, λ1与λ2的波段选择分别为671 nm和712 nm.Gitelson等(2007) 提出了用于估算陆地植被色素含量的三波段反演模型, 在对混浊富营养化的Chesapeake海湾水体中的叶绿素a浓度进行遥感反演时, 选择λ1、λ2和λ3的最佳位置分别为675、695和730 nm.Le等(2009) 在三波段模型的基础上, 考虑了悬浮颗粒物在近红外波段吸收和后向散射的影响, 提出了四波段模型, 并用其对太湖叶绿素a浓度进行了估算, 得到了较高的精度.但是, 这些方法在不同区域的特征波段选择和反演精度往往不同, 因此, 在特定区域利用遥感进行叶绿素a浓度监测之前需要对不同模型进行对比, 选择适合该区域的最佳模型.
太湖位于长江三角洲南缘, 对流域水生态系统具有重要作用.太湖面积约2338 km2, 最大水深3 m, 平均水深仅为1.89 m(秦伯强等, 2004), 湖泊动力比(湖泊面积的平方根/平均湖深)高达25.6(Bachmann et al., 2000), 属于典型的浑浊二类水体.太湖水体叶绿素a浓度随季节有显著的变化, 春、夏季特别是蓝藻水华爆发时叶绿素a浓度分布直接影响到水体的光学特性(李莉等, 2011).在太湖水体叶绿素a浓度的遥感反演模型对比方面, 李云亮等(2009) 通过对比分析三波段模型、两波段模型、荧光峰位置模型和一阶微分模型估算了1月太湖叶绿素a浓度的精度, 得到的结论为反射峰位置法估算精度最高.杨煜等(2009) 通过夏季太湖光谱实测数据, 建立了太湖叶绿素a浓度一阶微分模型、波段比值模型和三波段模型, 通过综合对比各反演模型, 认为三波段模型反演效果最佳.黄昌春等(2013) 使用三波段和四波段模型, 对中国不同区域的内陆水体进行叶绿素a浓度反演, 发现其精度存在着较大的时空差异.但这些现有研究仅利用地面高光谱测量数据进行对比分析, 而未利用卫星遥感数据对模型进行验证, 不能满足大区域动态遥感监测的要求.
本研究以太湖水域为研究区, 通过2015年5-7月实测反射光谱数据和同步水质化学分析数据, 综合使用多种叶绿素a定量反演方法, 探讨叶绿素a定量遥感反演的机制和模型, 明确春、夏季太湖水体的叶绿素a定量遥感反演的最佳波段和模型;然后将最佳模型应用于HJ-1A卫星搭载的高光谱仪(Hyperspectral Imaging Radiometer, HSI)遥感数据, 并对HSI高光谱遥感数据反演叶绿素a浓度结果进行评价.以期能为内陆二类水体叶绿素a浓度的光谱反演研究提供一些参考.
2 材料与方法(Materials and methods) 2.1 数据采集在2015年5-7月间, 结合无锡市环境监测中心站梅梁湖夏季蓝藻预警巡视和常规大环境的例行监测, 对太湖的19个点位(图 1)进行了11次水体光谱测量和水质采样分析.采样期间选择未发生水华且藻颗粒分布较均匀的水体, 共计采集了60个样点.水样采集后, 根据《水和废水监测分析方法》(国家环境保护总局, 2002)中关于叶绿素a的测定方法(丙酮-分光光度法), 对水样的叶绿素a浓度进行实验室测定.
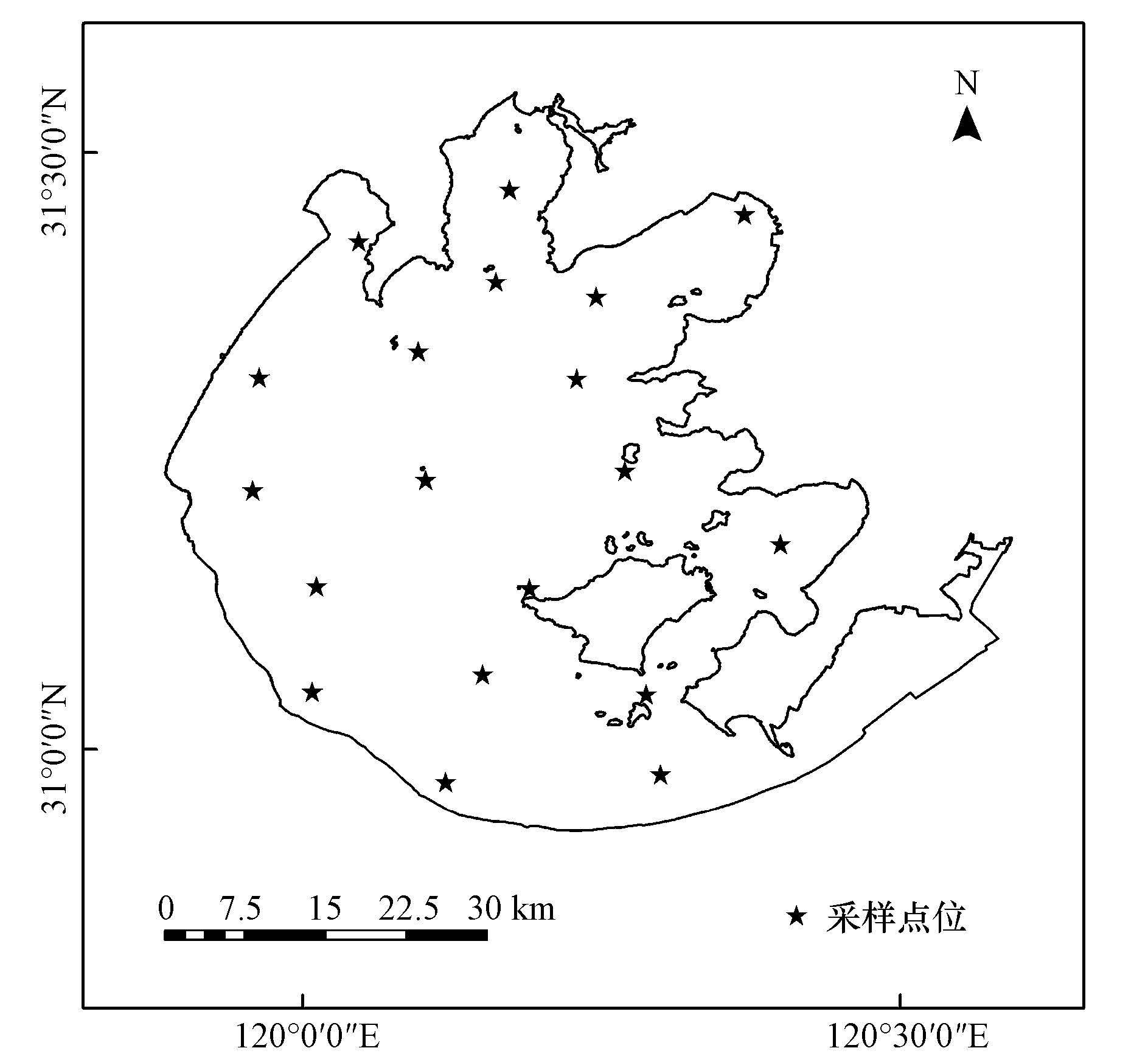 |
| 图 1 采样点位分布示意图 Fig. 1 Distribution of sampling stations |
本研究使用ASD Field Spec Pro FR便携式地物光谱仪, 光谱范围为350~1050 nm, 光谱分辨率为3 nm.仪器观测平面与太阳入射平面的夹角为135°左右(背向太阳), 仪器与水面法线的夹角在40°左右.水体测量结束后, 将仪器向上旋转90°左右, 对天空辐亮度进行测量(唐军武等, 2004).分别对标准灰板、水面和天空测量辐亮度, 每次测量采集10条光谱, 进行遥感反射比计算前, 首先剔除异常值, 再计算剩余光谱曲线的平均值, 最后使用平均处理后的数据计算遥感反射率Rrs(式(1) ).
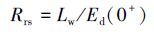
|
(1) |
式中, Lw为离水辐亮度(W·m-2·nm-1·sr-1), Ed(0+)为水面总入射辐照度(W·m-2·nm-1).Lw和Ed(0+)可以通过下列公式计算得到:

|
(2) |
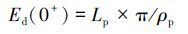
|
(3) |
式中, Lsw为离水总辐射度(W·m-2·nm-1·sr-1), Lsky为天空漫反射光辐亮度(W·m-2·nm-1·sr-1);r为气-水界面对天空光的反射率, 根据经验(唐军武等, 2004), 平静水面可取0.022, 风速为5 m·s-1左右时, r取 0.025, 风速为10 m·s-1左右时, r取0.026~0.028;Lp为标准灰板的辐亮度, ρp为标准灰板的反射率, 选用定标后反射率为24%~34%的灰板.
2.2 遥感数据本文选用的遥感数据为2015年8月3日过境太湖的两景HJ-1A卫星HSI高光谱数据, 编号分别为L20002582525和L20002582530.HSI高光谱成像仪采用干涉成像光谱技术, 拥有115个连续波段, 波段区间为0.45~0.95 μm, 光谱平均步长为4.32 nm, 幅宽50 km, 空间分辨率100 m, 重访周期96 h, 具有光谱分辨率高、光谱范围宽、重访周期短、稳定性较高等特点, 叶绿素a浓度反演各模型方法用到的波段均能在HSI数据中体现, 从而为空间尺度的水体叶绿素a定量反演提供了较为可靠的数据源.
2.2 模型方法 2.2.1 波段比值模型波段比值模型通常使用近红外波段最大反射率值和红光最小反射率值附近的2个波段的反射比估算叶绿素a浓度, 即R(NIR)/R(RED) (Han et al., 2003).
2.2.2 三波段模型三波段模型最早被Gitelson等(2003) 用于估算陆地植被色素含量.目前, 基于生物光学模型机理而推导出的三波段模型, 已在部分水域得到验证, 该类模型利用高光谱的3个波段数据对水体叶绿素浓度进行反演.由于具有一定的物理机理, 在波段选择上尽可能的减少其他水体组分的干扰, 因此, 模型在一定程度上适用性较好, 并具有较高的精度.三波段模型可用式(4) 表示.
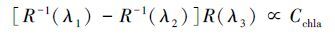
|
(4) |
式中, R-1(λi)为波段λi光谱反射率的倒数, Cchla为叶绿素a浓度(mg·L-1).其中, λ1应选择叶绿素a处于极大值的红光吸收峰附近;λ2目的在于去除黄色物质和悬浮物对水体吸收系数的影响, 应选择与λ1相邻的荧光峰波段;λ3位于的区域, 其水体的吸收应主要由纯水主导.Dall′ Olmo等(2005) 认为λ1、λ2和λ3的取值范围分别是660~690、700~750和≥730 nm.
2.2.3 荧光峰位置模型叶绿素荧光峰的波长是在红光/近红外区域反射率最大的波长(Rmax Red), Gitelson等(2003) 认为, 随着叶绿素a浓度的增高, 荧光峰位置会出现红移动现象.Vos等(1986) 通过对叶绿素a浓度为0~120 μg·L-1水体的研究, 得到叶绿素浓度的变化与荧光峰位置的移动呈指数关系的结论.
2.2.4 峰谷距离模型665 nm附近的反射谷和700 nm附近的荧光峰分别是由叶绿素a吸收和反射引起的.本文定义荧光峰与反射谷位置的差值为峰谷间的距离, 设为DP-V=λpeak-λvalley(图 2).
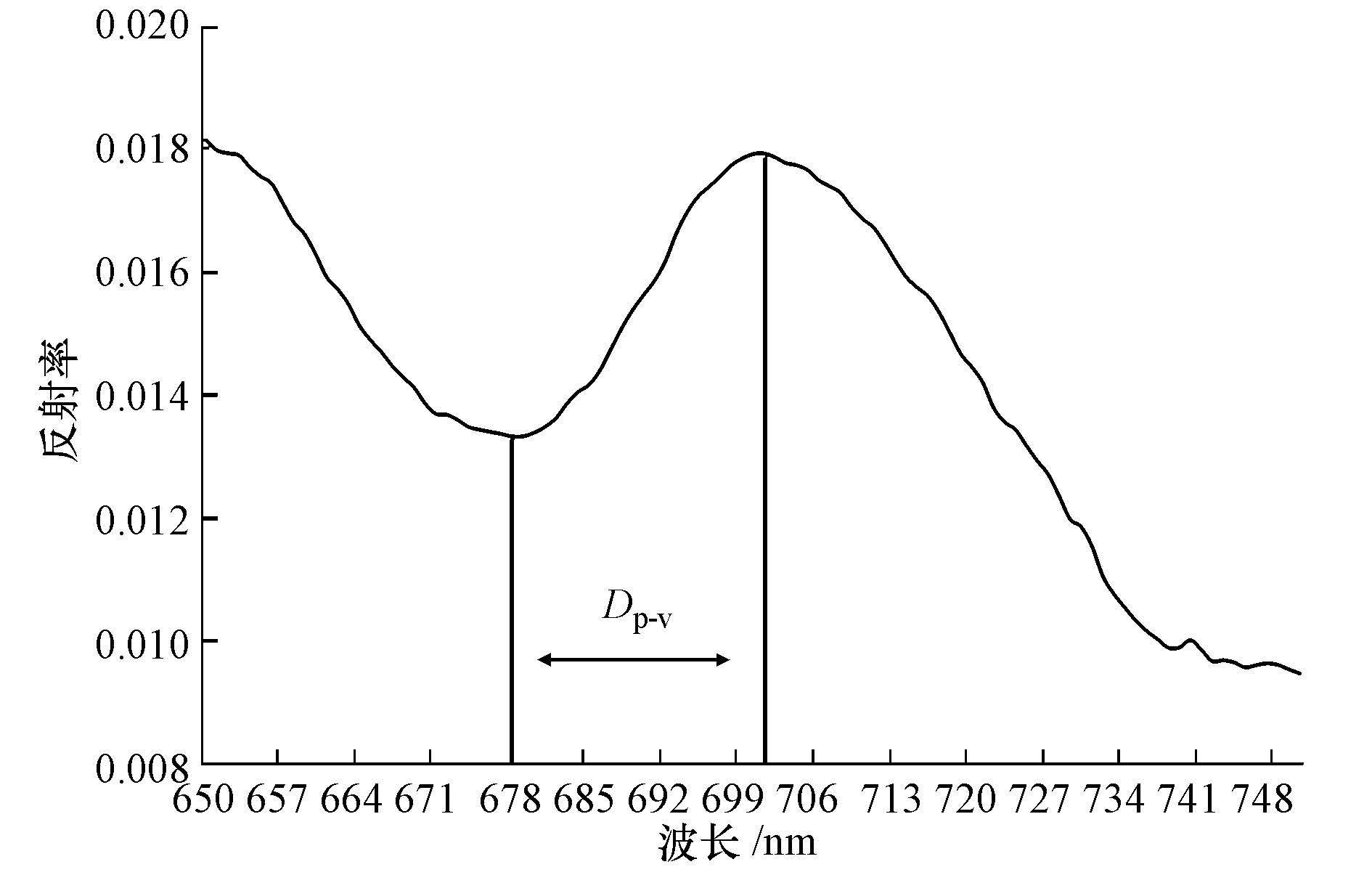 |
| 图 2 叶绿素a红波段峰谷距离示意图 Fig. 2 Illustration of the peak and valley distance in red band region |
一阶微分模型最早由Rundquist提出, 部分线性或近线性背景、噪声光谱对目标光谱的影响可以通过该方法去除(Rundquist et al., 1996).反射光谱经过微分模型的数学处理, 可以确定光谱拐点和最大、最小反射率波长的位置.Luoheng等(1997) 在对大量现场实测数据分析的基础上, 得出在叶绿素a浓度较高的情况下, 微分估算叶绿素a浓度效果最好的波长位置是690 nm.对于离散型的数据, 一阶微分可以通过式(5) 近似计算.
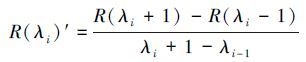
|
(5) |
式中, R(λi)′为波长λi处的反射光谱一阶微分, λi-1、λi、λi+1为相邻波长(nm).
2.2.6 NDCI模型Maisha等(1997) 提出一种新的叶绿素估算指数--归一化叶绿素指数(Normalized Difference Chlorophyll Index, NDCI), NDCI模型可用式(6) 表示.
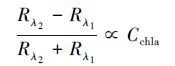
|
(6) |
式中, Cchla为叶绿素a浓度(mg·L-1), Rλ1和Rλ2分别为波段λ1、λ2处的反射率.NDCI指数采用归一化的形式, 可以部分消除太阳高度角的变化、大气辐射等因素带来的影响(EL Alem et al., 2012).λ1、λ2均应选择光学特性由叶绿素a主导的特征光谱处, 本文选择λ2为700 nm, λ1为 665 nm, 即NDCI=(R700-R675)/(R700+R675).
2.2.7 峰面积模型马万栋等(2014) 通过选取叶绿素荧光峰相邻的2个吸收谷(R674和R740)来计算叶绿素在红波段的反射峰面积(Normalized Peak Area, NPA), 并利用NPA反演了叶绿素a浓度, 取得了较优的结果.本文使用类似的方法, 通过选取叶绿素荧光峰相邻的两个吸收谷(Rλlv和Rλrv)计算叶绿素a在红波段的反射峰面积(图 3), 计算公式为:
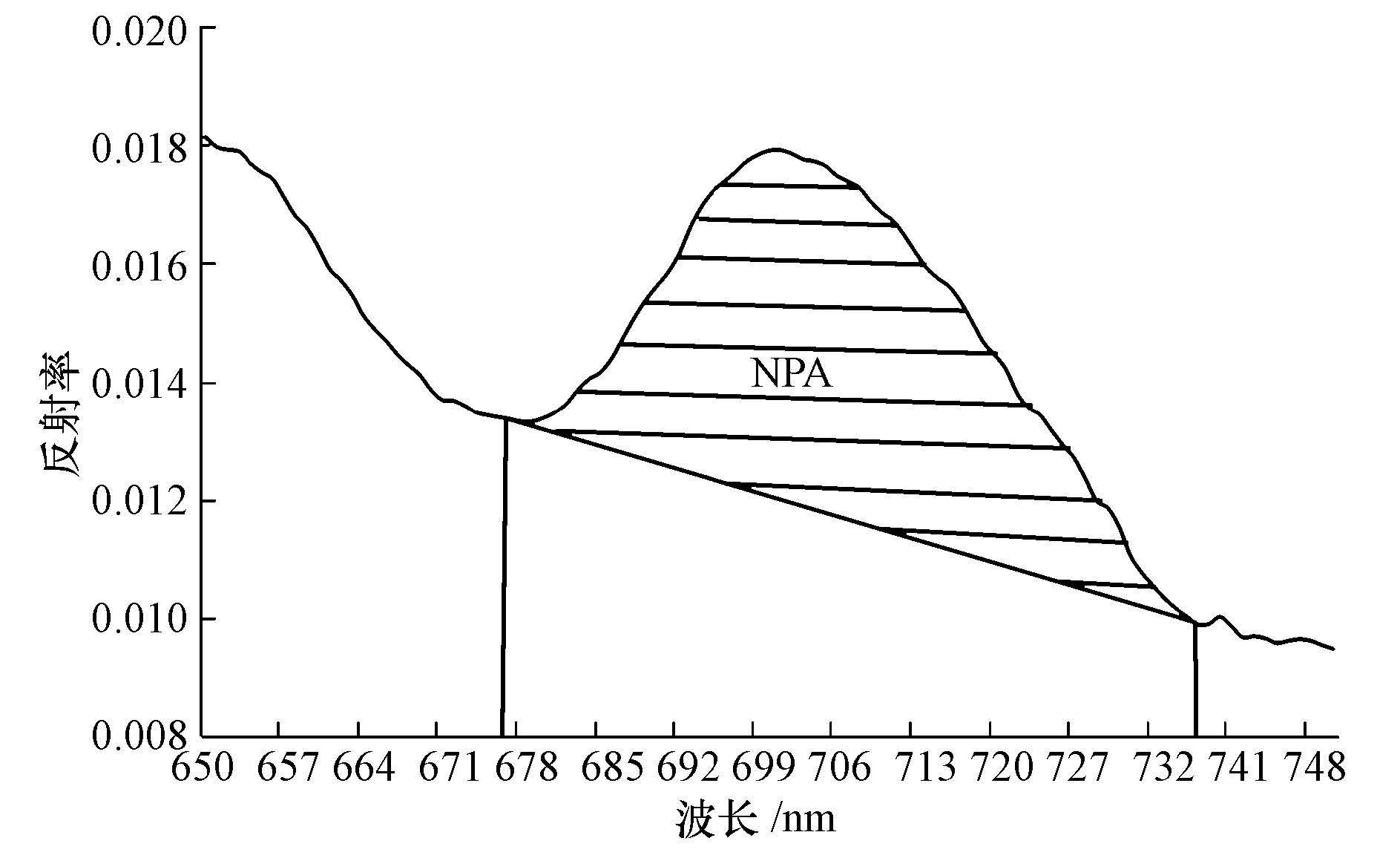 |
| 图 3 叶绿素a红波段反射峰面积示意图 Fig. 3 Illustration of the NPA in red band region of chlorophyll-a |
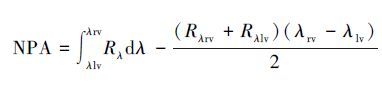
|
(7) |
式中, NPA是叶绿素a反射峰面积;Rλ是叶绿素a在波长λ处的反射率;λrv是荧光峰右侧吸收谷的波长(nm), λlv是荧光峰左侧吸收谷的波长(nm).
2.2.8 荧光峰高度模型叶绿素荧光峰高度的计算主要包括基线荧光高度法(Fluoresce Line Height, FLH)(Gower et al., 1980;1990) 和归一化荧光高度(Normalized Fluorescence Height, NFH)法, 本文采用荧光基线高度法.荧光基线高度法的基本原理是以荧光峰左右两侧吸收谷的连线为基线, 计算荧光峰的光谱反射率在基线之上的高度(图 4), 计算公式为:
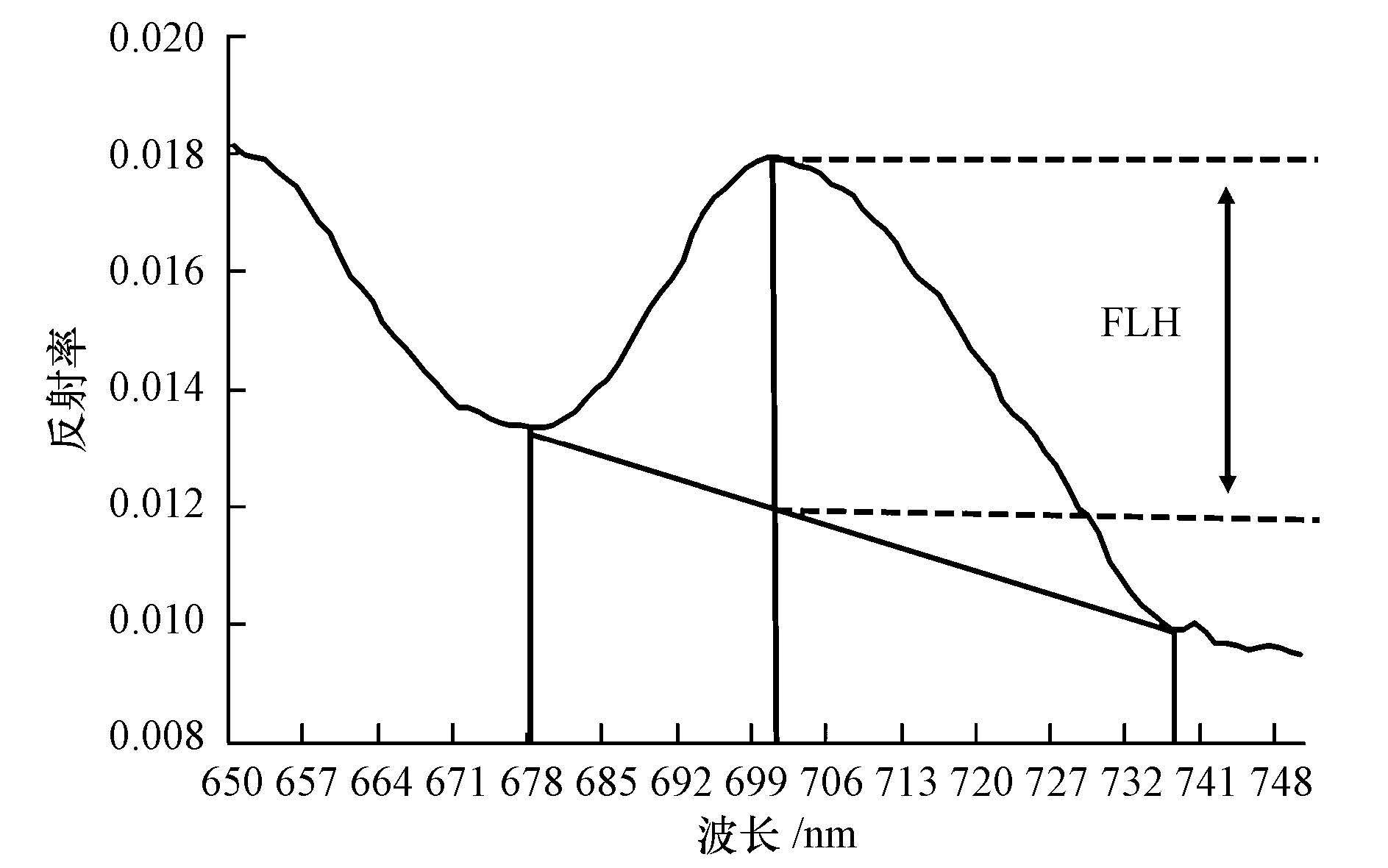 |
| 图 4 基线荧光高度示意图 Fig. 4 Illustration of the FLH |
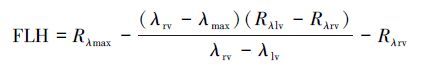
|
(8) |
式中, FLH为基线荧光高度;λmax是荧光峰波长(nm), λrv是荧光峰右侧吸收谷的波长(nm), λlv是荧光峰左侧吸收谷的波长(nm);Rλ是波长λ处的光谱反射率.
2.2.9 WCI模型王金梁等(2014) 通过借鉴陆地植被叶绿素监测指数MTCI(Meris Terrestrial Chlorophyll Index)的构建思路, 扩展研究了基于水体叶绿素a的监测指数WCI(Water Chlorophyll-a Index).WCI模型计算公式为:
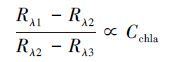
|
(9) |
式中, λ3选择叶绿素a的强吸收波段, λ1和λ2的选取使用与三波段模型类似的迭代方式, 首先分别使λ1、λ2初始化在光谱反射率的2个反射峰上, 再以相关系数为标准, 迭代优选另一波段.
2.2.10 四波段模型为了更好地减弱特别是近红外波段处悬浮颗粒的吸收和后向散射的影响, Le等(2009) 在三波段模型的基础上对其进行了改进, 引入了第4个近红外波段, 提出了四波段模型.四波段模型表达式如下:

|
(10) |
式中, λ1、λ2、λ3和λ4的取值范围分别是650~680、685~715、720~740和740~770 nm(孙德勇等, 2013).具体取值根据与实测叶绿素浓度a线性回归取最优可决系数进行迭代.
2.3 准确度评估本文使用均方根误差(RMSE)和平均绝对误差(MAPE)衡量反演模型的精度, 计算公式分别为:

|
(11) |

|
(12) |
式中, ximea代表水体光谱使用相关模型计算的水体叶绿素a浓度(mg·L-1);ximod代表实验室检测的叶绿素a浓度(mg·L-1);n为样本数.
3 数据分析(Data analysis) 3.1 光谱特征分析绘制60个采样点的光谱曲线, 结果如图 5所示.从光谱曲线上看, 5-7月太湖水体遥感反射率光谱表现为较典型的内陆水体特征.400~500 nm区域水体反射率较低, 这主要是因为叶绿素a和黄色物质对该范围内光能量较强的吸收;叶绿素和胡萝卜素对光能量的弱吸收及细胞的散射作用, 在550~580 nm范围内形成了一个反射峰, 此反射峰可以作为叶绿素浓度的定量标识;藻蓝素在620~630 nm波段的吸收, 导致了反射谷的形成;由于670 nm附近叶绿素a对红光波段的强烈吸收(Yacobi et al., 1995), 导致也出现了反射谷;685~715 nm光谱段出现的荧光峰是含有藻类水体最为重要的特征, 反射峰的位置和数值可以用于指示叶绿素a浓度(Fischer et al., 1990), 荧光峰位置具有随着叶绿素浓度的增高出现红移的现象.由于水在近红外范围内强吸收, 730~790 nm范围内反射率均较低, 其中, 760 nm左右出现的一个小的反射峰可能是由于水体内的氧气吸收.在810 nm附近再次形成反射峰, 可能是纯水的性质与悬浮物散射作用(Chi et al., 2003)综合造成的.
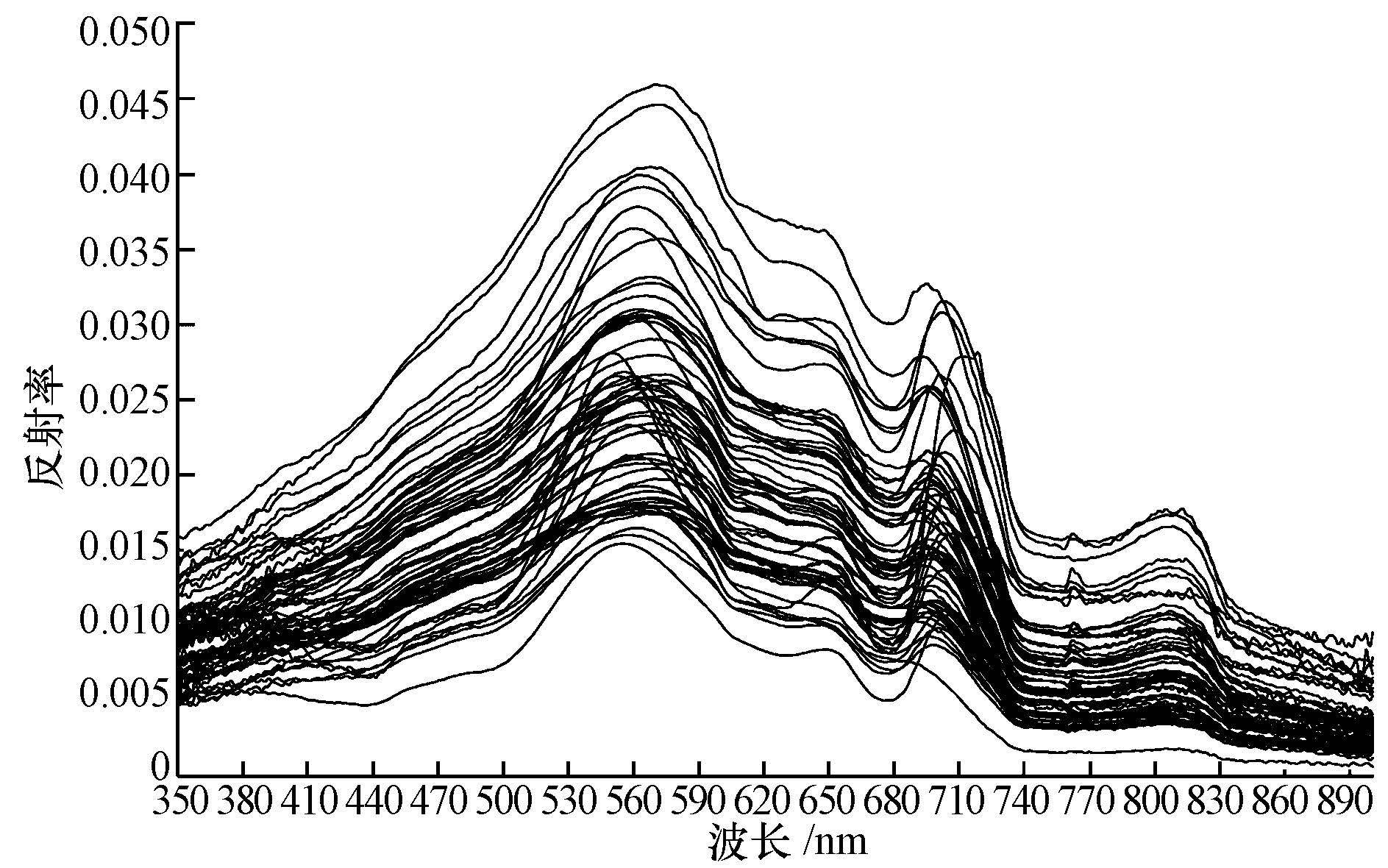 |
| 图 5 采样点光谱曲线 Fig. 5 Spectral curves of sampling points |
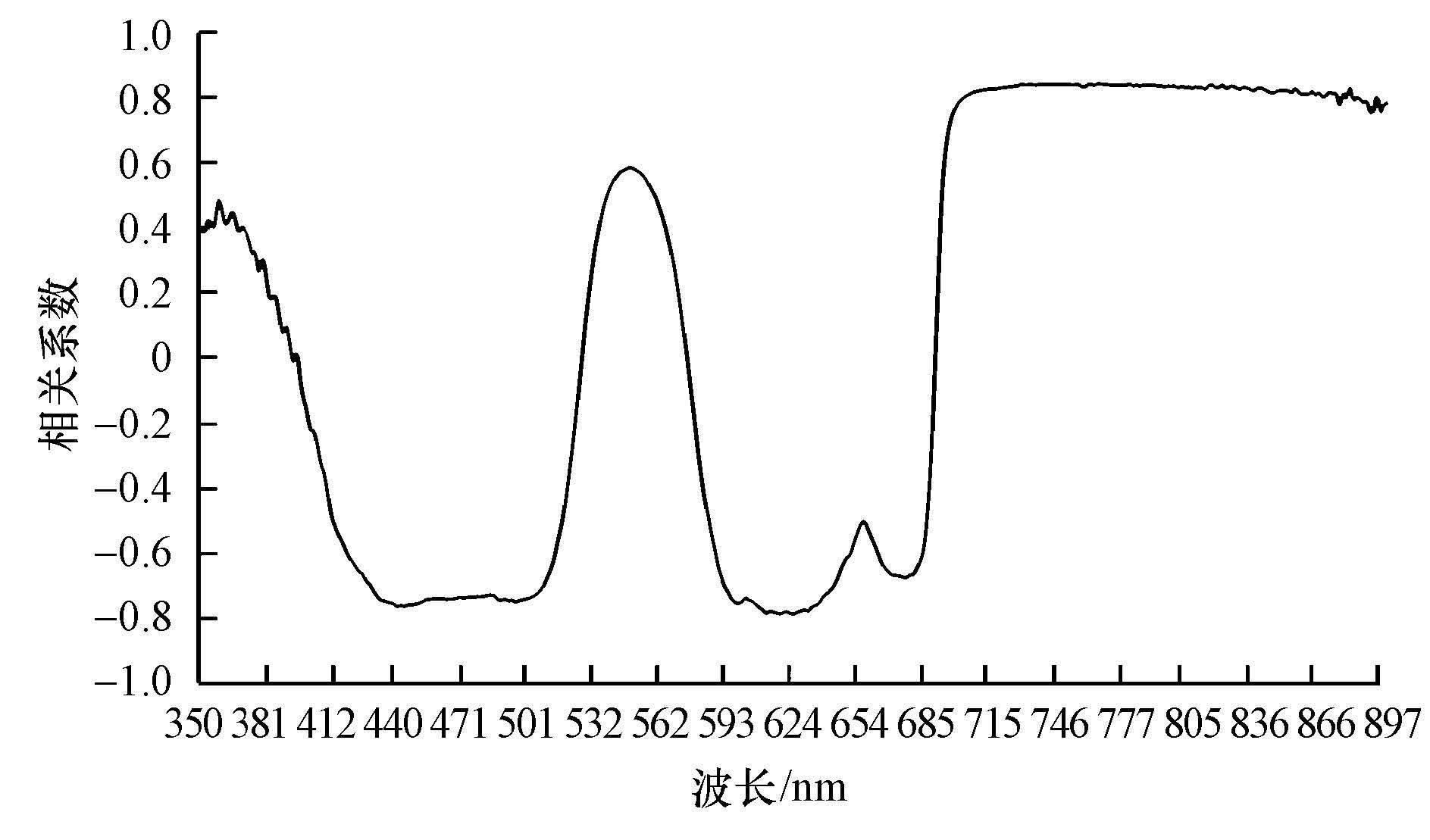
在进行光谱测量时, 由于周围环境的影响、天气的变化及测量角度的变化都会影响反射率数值的大小, 对于60个用于估算分析的样点, 首先对每条反射光谱用其从450 nm到750 nm的反射率平均值做归一化处理(李素菊等, 2002).图 6为归一化后各波段反射率与叶绿素a浓度的相关关系曲线图.
 |
| 图 6 归一化反射率和叶绿素a浓度的相关性分析 Fig. 6 Correlation analysis between normalized reflectance and chlorophyll-a concentration |
从图 6可以看出, 440~500 nm处负相关系数较大, 这可能是由于蓝紫光被叶绿素吸收导致;624 nm附近较大的负相关系数对应着藻蓝素的吸收峰, 说明太湖5-7月藻类的优势种为蓝藻;560 nm附近正相关系数较大, 这可能是由于叶绿素与悬浮物的协同作用所引起;670 nm附近负相关系数较大, 此种现象是由于该波段叶绿素的吸收作用, 叶绿素的强反射导致了700 nm之后正相关系数较大.本文使用相关性较高、物理意义较明确的665 nm和700 nm处的反射率参与部分模型对叶绿素a浓度的估算.
3.3 不同模型估算叶绿素a浓度分析在测量的60个样本中, 叶绿素a浓度跨度为0.002~0.132 mg·L-1.本研究利用太湖水体的实测光谱数据得到反射率, 对反射率进行归一化处理后, 使用比值、三波段、荧光峰位置、峰谷距离、一阶微分、归一化叶绿素指数(NDCI)、峰面积、荧光峰高度模型、WCI和四波段模型进行叶绿素a浓度的估算.针对这10种反演模型算法, 在太湖2015年5-7月野外实测的遥感反射率数据和同步叶绿素浓度数据的60组数据中, 使用2/3的数据进行建模, 1/3的数据进行验证.其中, 波段比值模型使用700 nm附近的反射率峰值Rrs(700) 与665 nm附近的反射率谷值Rrs(665) 作比值;WCI模型λ3选择反射率谷值处的665 nm, λ1和λ2通过循环迭代确定为684 nm和629 nm;四波段和三波段模型根据模型估算与实测叶绿素a浓度相关系数最大的原则, 通过循环迭代选取最佳的波段, 最终确定四波段λ1、λ2、λ3和λ4分别为677、708、733和756 nm, 三波段λ1、λ2和λ3分别为679、708和767 nm;一阶微分模型在697 nm处与叶绿素a浓度的相关系数最大;NDCI模型λ1、λ2的选择分别是665 nm和700 nm;荧光峰位置模型、峰谷距离模型、峰面积模型、荧光峰高度模型中参与运算波段的选择根据光谱曲线的实际情况进行选取.
使用2/3的数据样本(40组)作为校正数据集, 将以上确定最优波段后的因子作为变量与实测的叶绿素a浓度进行回归分析, 分别建模后, 由各方法估算的叶绿素a浓度与实测叶绿素a浓度建立的反演模型如表 1所示.四波段模型的决定系数最高, 达到0.8256;三波段模型、一阶微分模型、峰谷距离模型、荧光峰位置模型、WCI模型、比值模型和NDCI模型的决定系数也较高, 分别为0.8134、0.7933、0.7866、0.7713、0.7266、0.7217和0.7196;荧光峰高度模型和峰面积模型决定系数相对较低, 分别为0.6975和0.6716.
| 表 1 不同方法叶绿素a反演模型 Table 1 Chlorophyll-a retrieval model in different methods |
剩余1/3的数据样本(20组)作为验证数据集, 用于10种叶绿素a模型反演精密度的评价.对比这10种反演模型的反演结果(图 7), 可以看到, 四波段模型反演效果最好, 决定系数为0.7798, MAPE为27.86%, 其后依次为三波段模型、比值模型、一阶微分模型、荧光峰高度模型、峰面积模型、峰谷距离模型、荧光峰位置模型、NDCI模型和WCI模型, MAPE分别为28.08%、29.59%、34.47%、34.61%、34.75%、35.35%、38.28%、38.86%和45.11%.由表 1和图 7可知, 相较于其他模型, 四波段模型在春、夏季太湖水域反演结果最好, 应用效果也最好, 三波段模型的反演结果与应用效果也较好, 其余模型方法的反演结果与应用效果之间并没有较明显的关系.
 |
| 图 7 10种模型叶绿素a浓度估算值与实测值的对比 (a.波段比值;b.三波段;c.荧光峰位置;d.峰谷距离;e.一阶微分;f.NDCI;g.峰面积;h.荧光峰高度;i.WCI;j.四波段) Fig. 7 Comparison between measured and estimated the chlorophyll-a concentration based on ten model |
本文通过2015年8月3日过境太湖区域的两景HSI影像与地面同步采样数据, 使用前述评价精度最高的四波段模型, 应用于卫星遥感数据对叶绿素a浓度的估算和评价.
3.4.1 HSI遥感影像的预处理辐射定标:利用中国资源卫星应用中心提供的辐射定标参数将HSI影像由DN值转化为辐亮度.
几何精校正:采用已经过几何精校正的太湖流域Landsat8 OLI数据为参考影像(UTM投影, WGS84地理坐标系), 在ENVI5.1的支持下对HSI高光谱影像进行几何精校正, 图像重采样方法使用3次卷积内插的多项式纠正方法, 误差控制在1个象元左右.
大气校正:使用同步MODIS(Moderate-Resolution Imaging Spectroradiometer)数据(与HSI成像时间相差0.5 h左右)辅助的基于Gordon大气校正模型的改进算法, 该校正方法经相关研究验证, 其校正精度平均可达到80%左右(李俊生等, 2006;王海君, 2007;檀静, 2013).本文在Gordon瑞利单次散射的基础上进行近似计算(Gordon et al., 1994), 在水体-大气系统下, 传感器接收到的辐射由5部分组成:

|
(13) |
式中, Lp(λi)为大气程辐射;Lg(λi)是太阳耀斑辐射;Lw(λi)是离水辐射;Lwc(λi)是水面白帽辐射;Lwb(λi)是来自水底的辐射, 对二类水体和水深超过一定深度的一类水体值为0, 在通常的水色遥感中可以忽略不计(唐军武等, 2005);T(λi)、t(λi)分别为各个波段的直射、漫射透过率.对于从天顶观测获得的遥感影像数据, 当没有出现突变值时, 可以忽略太阳耀斑的影响(李俊生等, 2006);当风速不大时, 白帽辐射也可忽略.因此, 传感器接收到的辐射可以简化为:
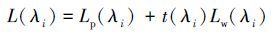
|
(14) |
大气漫射透过率t(λi)主要受大气分子散射、臭氧吸收及气溶胶散射等因素的影响, 可按(15) 式计算(唐军武, 1998).

|
(15) |
式中, τr(λi)为大气分子瑞利散射垂直光学厚度;τOZ(λi)为臭氧垂直光学厚度;θi为太阳或者观测天顶角.
太阳程辐射Lp(λ)主要是由大气分子散射和大气中的悬浮气溶胶散射造成的, 又可分为瑞利散射辐射Lr(λ)和气溶胶散射辐射La(λ).其中, 瑞利散射Lr(λ)在Gordon业务化算法中已较为成熟与精确, 可按下式近似计算:
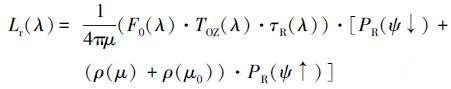
|
(16) |
式中, F0(λ)为大气层外太阳辐照度, 与日地距离有关;TOZ(λ)为臭氧吸收引起的透过率, 与臭氧光学厚度有关;τR(λ)为瑞利光学厚度, 与实测大气压力有关.PR(Ψ↓)和PR(Ψ↑)分别为入射光和散射光的瑞利相位函数, 与太阳及卫星的天顶角、方位角有关;ρ为菲涅耳反射率, 与水体折射率有关;μ0、μ分别为太阳天顶角和卫星天顶角的余弦.
对于气溶胶散射辐射, 本文使用同步MODIS数据辅助进行估算.针对一类水体, Gordon假设MODIS近红外波段第15波段(744~755 nm)和第16波段(857~872 nm)对应的离水辐亮度为0.而太湖作为二类水体, 其光学特性受悬浮物和黄色物质影响较大, 导致其在近红外波段的离水辐亮度大于0.因此, 根据相关研究(李俊生等, 2006), 本文使用离水辐亮度近似为0的MODIS第5(1230~1250 nm)和第6(1628~1652 nm)的短波红外波段进行辅助估算.
假设HSI数据的气溶胶类型在小范围内不变, 因此, 气溶胶散射相函数和单次散射反照率随波长的变化不大, 在只考虑单次气溶胶散射的情况下, 2个波长的单次散射反射率具有比例的关系, 即可定义一个大气校正参数ε进行计算(Wang et al., 1994), 表达式如下所示:
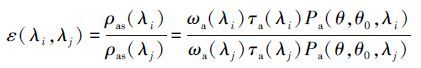
|
(17) |
式中, λi为短波波长(nm), λj为长波波长(nm), 选择离水辐亮度为0的波段计算ε.ωa、τa分别为气溶胶单次散射反照率和气溶胶光学厚度.对于同一种气溶胶模型来说, ωa可以认为是定值, 而单次散射相函数Pa是观测几何与波长λ的函数, 对大量实测数据的统计研究发现, 单次散射相函数之比也可以看作常数(Richard et al., 1990).从而式(17) 可简化为两个波长处气溶胶厚度之比, 根据大量气溶胶观测结果, 一个合理的假设是(Wang et al., 1994):
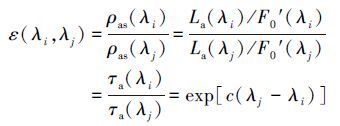
|
(18) |
式中, c为气溶胶类型参数.F′0(λ)为经过臭氧吸收订正的大气层外太阳辐照度, 与臭氧层光学厚度有关.
通过MODIS第5和第6波段数据辅助, 假设在比较清洁的水体, Lw(λ1240)≈0, Lw(λ1640)≈0, Lrλ1240和Lr(λ1640)已知, 且忽略太阳直射反射和白帽影响, 则:
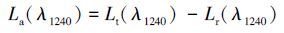
|
(19) |

|
(20) |
式中, Lt(λ)从MODIS影像上直接读取, Lr(λ)根据前述公式精确计算, 从而可以公式(21) 计算得到气溶胶参数c.
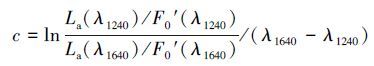
|
(21) |
然后将待求各波段的等效波长及臭氧修正的大气顶层辐照度数据代入式(22) , 从而得到各波段对应的气溶胶散射.于是便可得到HSI数据各波段的离水辐亮度LW(λi) (式(23) ), 进而得到各波段的遥感反射率(式(24) ).
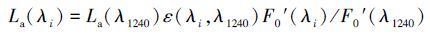
|
(22) |
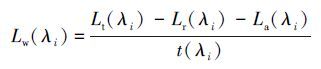
|
(23) |
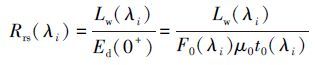
|
(24) |
式中, t(λi)为卫星方向的大气漫射透过率, 通过式(15) 计算得到;Ed(0+)为水表面下行辐照度;t0(λi)为太阳方向的大气漫射透过率.
HSI影像重构:由于各种因素的影响, HSI获取的数据存在条带噪声(童庆禧等, 2008), 主要是由于传感器响应不均匀而造成的影像在一定方向上出现的灰度值连续偏高或者偏低的现象(石光明等, 2008;计忠瑛等, 2004).高光谱影像的数据质量受条带噪声的影响较大, 所以需将条带噪声去除.
本文依据Schmeltz等(2010) 的研究, 在大气校正的基础上, 利用与环境小卫星HSI影像同步成像的环境小卫星CCD数据进行高光谱重构.其表达式如下:
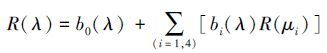
|
(25) |
式中, R(λ)为重构的高光谱遥感反射率, λ为HSI数据的中心波长(nm);b0λ为常数项, biλ为第i个自变量的线性拟合系数;Rμi)为CCD 4个通道的遥感反射率.
避开水华区, 在HSI影像上均匀取50个点, 以这50个点的HSI与CCD遥感反射率为数据集, 利用SPSS18.0软件做多元线性回归, 拟合得到b0(λ)、b1(λ)、b2(λ)、b3(λ)和b4(λ)这5个参数, 即可得到波段λ处的光谱重构表达式.将CCD影像数据4个通道的反射率代入每个HSI每个波段的重构模型, 即可得到同时具有115个波段和30 m空间分辨率的重构影像.
3.4.2 四波段模型应用于HSI数据反演叶绿素a浓度根据太湖2015年8月3日实地采集样点的11个经纬度坐标, 提取出经相关预处理后HSI影像上这11个样点的光谱反射率数据.将水体实测光谱建立的四波段模型应用于重构后的HSI数据中, 与实测11个样点的叶绿素a浓度进行线性回归, 由四波段模型估算的叶绿素a浓度与实测叶绿素a浓度的关系如图 8所示.估算值与实测值的R2、RMSE和MAPE分别为0.7643、0.00433 mg·L-1和45.62%.由此可见, 四波段模型能够较好地应用在基于HSI高光谱数据在春、夏季太湖叶绿素a浓度反演中, 且反演精度较高, HSI高光谱数据在内陆二类水体叶绿素a浓度反演方面有较好的应用前景.根据四波段法的估算方程, 反演得到的太湖2015年8月3日叶绿素a浓度分布合成图如图 9所示.需要说明的是, 太湖西部的高值区是由水华所导致, 而贡湖、胥湖及东太湖的高值区, 则主要是因为这些区域有较多的水生植物分布.
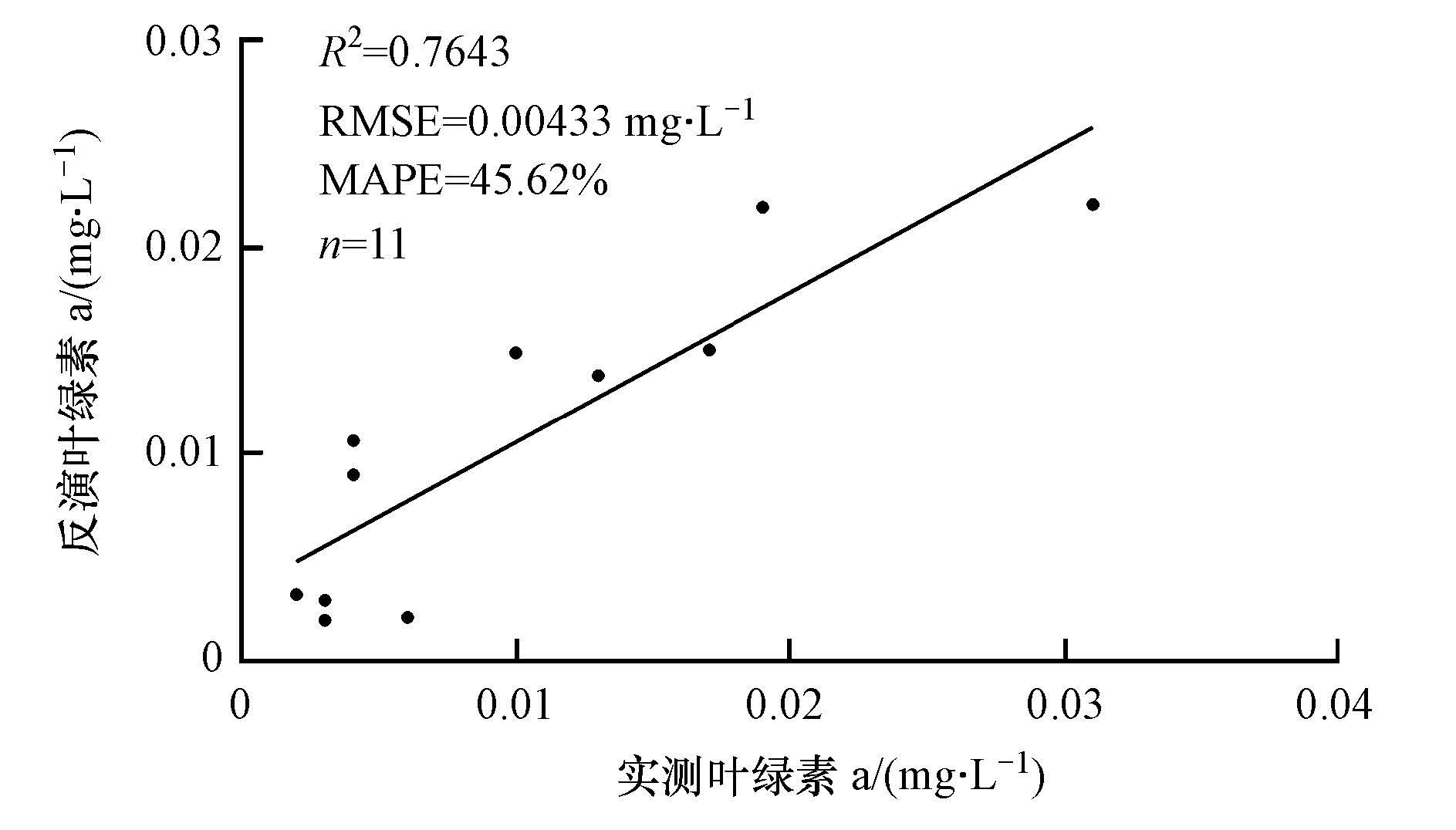 |
| 图 8 HSI数据四波段模型叶绿素a浓度估算值与实测值对比 Fig. 8 Comparison between measured and estimated the chlorophyll-a concentration based on four band model using HSI data |
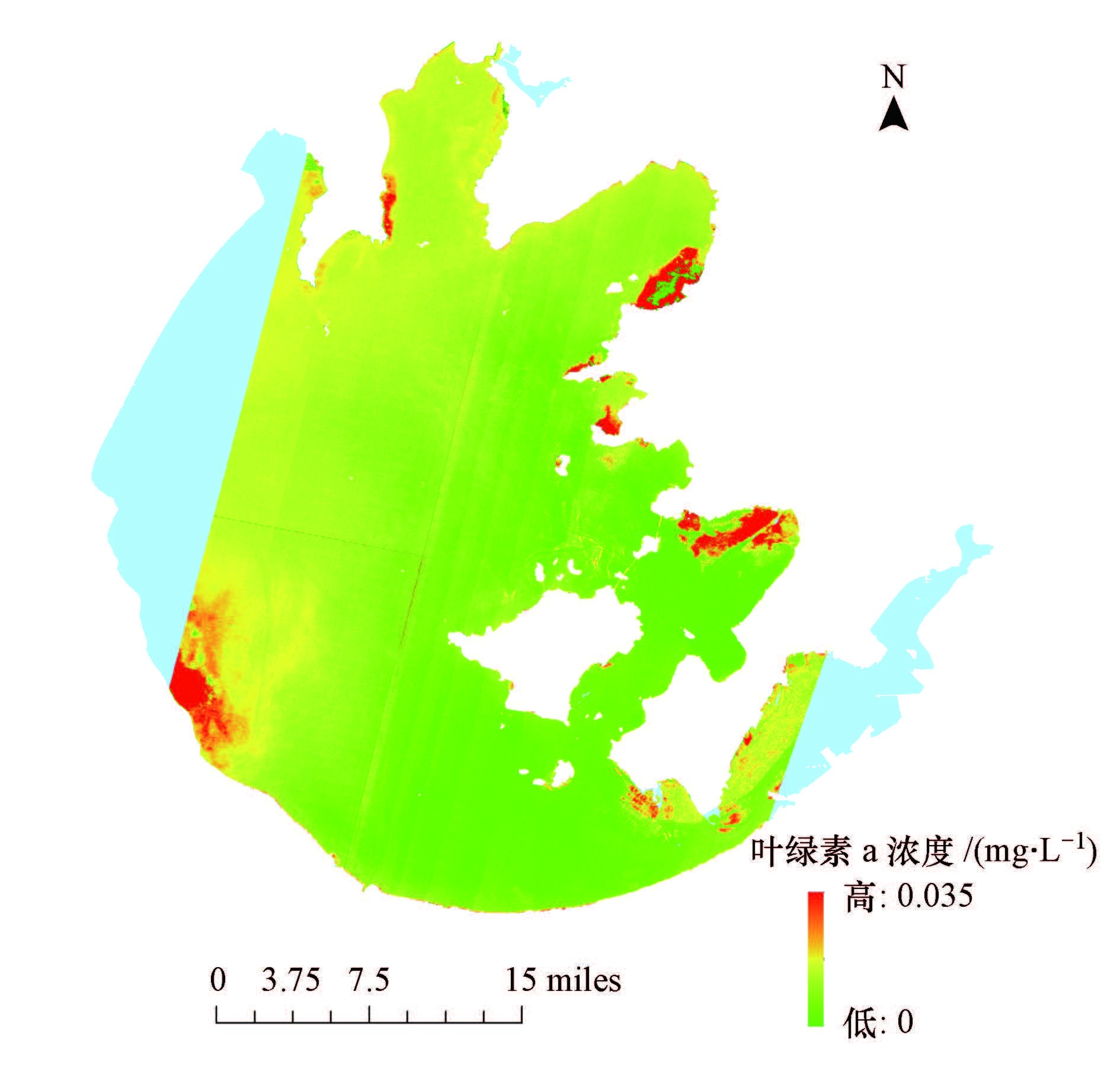 |
| 图 9 HSI数据太湖叶绿素a浓度四波段模型分析结果 Fig. 9 Four band model result of chlorophyll-a concentration of Lake Taihu using HSI data |
本研究利用5-7月春、夏季太湖实测光谱数据, 在研究水体光谱反射率曲线的基础上, 选取特征波段或波段组合建立了不同叶绿素a浓度光谱反演模型, 通过对光谱反射率数据的研究及不同反演模型对比分析, 在一定程度上对各类模型反演叶绿素a浓度的精度进行了评估.波段比值模型、三波段模型、荧光峰位置模型、峰谷距离模型、一阶微分模型、NDCI模型、峰面积模型、荧光峰高度模型、WCI模型和四波段模型是以特定水体光学特性建立的模型, 但由于不同水体光学特性的差别, 导致了模型适用性的不同.
三波段模型是基于水体光谱反射率与其固有光学特性之间关系构建的模型, 通过3个波段的选择, 使叶绿素a的吸收特征得到了最大程度的体现, 同时减小了水体中黄色物质和悬浮物对吸收和后向散射的影响, 从而有益于叶绿素a浓度反演.但三波段模型假设近红外波段悬浮物的吸收和散射远小于纯水的吸收, 对于高浑浊水体, 近红外波段处的吸收和散射不可忽略, 四波段模型是对三波段模型的进一步改进, 与三波段模型相比, 四波段模型消除了近红外波段悬浮物吸收和后向散射的影响, 并将水吸收的影响最小化.本研究得到的四波段和三波段模型的反演结果与应用效果都比较好, 其中, 四波段模型最佳.当叶绿素a浓度较高时, 一阶微分模型反射率微分估算叶绿素a浓度的效果也较好, 反之, 在低叶绿素a浓度的情况下精度就会降低.荧光峰位置变化模型与峰谷距离模型反演结果较好, 但应用效果却不甚理想, 反演结果较好首先与校正数据集的浓度跨度比较大、叶绿素浓度分布较为均匀有关, 其次是因为悬浮物颗粒和黄色物质对荧光峰位置的影响比较小, 且不受测量光谱角度、地表辐射照度等变化的影响;而验证数据集叶绿素a浓度跨度则相对较小, 这就导致了应用效果较差.反射峰面积与荧光峰高度模型不仅考虑了水体中悬浮物、黄色物质及水体的后向散射对叶绿素a浓度反演造成的影响, 而且还综合考虑了叶绿素弹性散射效率的影响, 同其它模型相比而言, 反演精度差别不大.采用波段比值模型和NDCI模型, 可以减少数据处理的工作量, 本文采用叶绿素吸收峰和反射峰所在的波段(665 nm和700 nm), 其中, NDCI模型验证数据集的反演精度较其它模型较低(38.29%), 但也在可接受的范围内, 对于春、夏季太湖叶绿素a浓度的光谱反演, 也是可以考虑的方法.WCI模型验证数据集的反演精度较其它模型最低(45.11%), 其反演结果较实测值明显偏高, 该模型对春、夏季太湖水域相对不适用.
四波段模型4个波长的位置均位于红光和近红外, 大多数卫星传感器上均有对应的通道, 具有较广泛的适用性.将地面光谱数据建立得到的四波段模型应用到HSI高光谱遥感影像的叶绿素a浓度反演中, 由此得到的精度也较高, 但较地面试验结果有所降低.这首先与HSI高光谱影像数据存在一定程度的条带与噪声有关, 本文虽对HSI数据进行了影像重构降噪, 但仍有不可避免的影响;其次, 大气校正的精准程度也对反演结果精密度的高低有着一定的关系.
四波段模型与三波段模型均是具备物理机理的半经验半分析模型, 在波段选择上尽可能地减少其他水体组分的干扰, 因此, 模型适用性较好, 且具有较高的精度.但由于不同水体中水体组分的差异性造成了水体光学特性的差异, 进而影响着不同的水体光谱特征.水体组成及其生物光学特性的不同造成反演因子最佳波段位置和反演参数存在较大的变异性, 同时统计模型中的参数受样本变化的影响较大, 对于各模型包括四波段模型反演叶绿素a浓度的普适性有较大的影响.例如, 四波段模型相对于三波段模型, 增加1个波段用于减小近红外波段颗粒物吸收系数对叶绿素反演结果影响, 进而提高叶绿素四波段模型反演精度, 但由于二类水体组分和光学特性有较大的时空差异, 当色素颗粒物吸收系数较大, 近红外颗粒物吸收系数较小时, 四波段增加了1个波段的同时也增加反演模型的不确定性, 很有可能较低模型的反演精度.
5 结论(Conclusions)使用波段比值、三波段、荧光峰位置、峰谷距离、一阶微分、NDCI、峰面积、荧光峰高度、WCI和四波段模型, 对太湖夏季叶绿素a含量进行反演与评估, 建模得到的四波段模型决定系数最高, 峰面积模型的决定系数相对最低;四波段模型的反演精度最高, 而WCI模型反演精度相对最低.将反演精度最高的四波段模型应用于HSI高光谱影像数据, 也得到较高精度.本次试验是在5-7月春、夏季期间进行的, 且60个样点均选择藻颗粒分布均匀的水体, 因此, 对模型的精度评价结果仅适用于太湖春、夏季蓝藻占优势种、叶绿素对水体光学特性占主导作用, 且叶绿素分布均匀的水体.由于不同季节湖区的水质情况各不相同, 对所建立模型的精度评价并不能反映全年不同时期的水质情况, 因此, 将继续进行秋、冬季水体光谱的采集工作, 并综合运用各模型, 开展太湖水域各时期的叶绿素a浓度光谱反演工作.
| [${referVo.labelOrder}] | 安如, 刘影影, 曲春梅, 等. 2013. NDCI法Ⅱ类水体叶绿素a浓度高光谱遥感数据估算[J]. 湖泊科学, 2013, 25(3) : 437–444. |
| [${referVo.labelOrder}] | Bachmann R W, Hoyer M V, Canfield D E. 2000. The potential for wave disturbance in shallow Florida Lakes[J]. Lake and Reservoir Management, 16(4) : 289–291. |
| [${referVo.labelOrder}] | Chi K Y H, Koh S T. 2003. Spectral irradiance profiles of suspended marine clay for the estimation of suspended sediment concentration in tropical waters[J]. International Journal of Remote Sensing, 24(16) : 3235–3245. DOI:10.1080/01431160110114934 |
| [${referVo.labelOrder}] | Daniel O, Anatoly G, Vittorio E B, et al. 2012. Review of constituent retrieval in optically deep and complex waters from satellite imagery[J]. Remote Sensing of Environment, 118(4) : 116–126. |
| [${referVo.labelOrder}] | Dall' Olmo G, Gitelson A A. 2005. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive water:Experimental results[J]. Applied Optics, 44(3) : 412–422. DOI:10.1364/AO.44.000412 |
| [${referVo.labelOrder}] | EL-Alem A, Chokmani K, Laurion I, et al. 2012. Comparative analysis of four models to estimate chlorophyll-a concentration in case case-2 waters using MODerate resolution imaging spectroradiometer (MODIS) imagery[J]. Remote Sensing, 4(8) : 2373–2400. |
| [${referVo.labelOrder}] | Fischer J, Krounfeld V. 1990. Sun-stimulated chlorophyll fluorescenceⅠ:Influence of oceanic properties[J]. Remote Sensing, 11 : 2125–2147. DOI:10.1080/01431169008955166 |
| [${referVo.labelOrder}] | Gordon H R, Wang M H. 1994. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS:a preliminary algoritjm[J]. Applied Optics, 33(3) : 443–452. DOI:10.1364/AO.33.000443 |
| [${referVo.labelOrder}] | Gordon H R, Morel A Y. 1983. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery:A review[M]. Berlin: Springer Science & Business Media. |
| [${referVo.labelOrder}] | Gitelson A A, Schalles J F, Hladik C M. 2007. Remote chlorophyll-a retrieval in turbid,productive estuaries:Cheapeake bay case study[J]. Remote Sensing of Environment, 109 : 464–472. DOI:10.1016/j.rse.2007.01.016 |
| [${referVo.labelOrder}] | 国家环境保护总局编. 2002. 水和废水监测分析方法[M]. 北京: 中国环境科学出版社. |
| [${referVo.labelOrder}] | Gitelson A A, Gritz Y. 2003. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for nondestructive chlorophyll assessment in higher plant leaves[J]. Journal of Plant Physiology, 160(3) : 271–282. DOI:10.1078/0176-1617-00887 |
| [${referVo.labelOrder}] | Gower J F R, Borstad G A. 1990. Mapping of phytoplankton by solar-stimulated fluorescence using an imaging spectrometer[J]. International Journal of Remote Sensing, 11 : 313–320. DOI:10.1080/01431169008955022 |
| [${referVo.labelOrder}] | Gower J F R. 1980. Observation of in situ fluorescence of chlorophyll-a in Saanich Inlet[J]. Boundary-Layer Meteorology, 18(3) : 235–245. DOI:10.1007/BF00122022 |
| [${referVo.labelOrder}] | Honeywill C, Paterson D M, Hegerthey S E. 2002. Determination of microphytobenthic biomass using pulse-amplitude modulated minimum fluorescence[J]. European Journal of Phycology, 37(4) : 485–492. DOI:10.1017/S0967026202003888 |
| [${referVo.labelOrder}] | Huang C C, Zou J, Li Y M, et al. 2014. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 93 : 29–39. DOI:10.1016/j.isprsjprs.2014.03.012 |
| [${referVo.labelOrder}] | 黄昌春, 李云梅, 徐良将, 等. 2013. 内陆水体叶绿素反演模型普适性及其影响因素研究[J]. 环境科学, 2013, 34(2) : 525–531. |
| [${referVo.labelOrder}] | Hoogenboom H J, Dekker A G, Althuis I J A. 1998. Simulation of AVIRIS sensitivity for detecting chlorophyll over coastal and inland water[J]. Remote Sensing of Environment, 65(3) : 330–340. |
| [${referVo.labelOrder}] | Han L, Donald C, Rundquitst D C. 2003. Comparison of NIR/RED ratio and first derivative of reflectance in estimating chlorophyll[J]. International Journal of Remote Sensing, 24(16) : 3235–3245. DOI:10.1080/01431160110114934 |
| [${referVo.labelOrder}] | 计忠瑛, 相里斌, 王忠厚, 等. 2004. 干涉型超光谱成像仪的星上定标技术研究[J]. 遥感技术与应用, 2004, 19(4) : 280–283. |
| [${referVo.labelOrder}] | Le C F, Li Y M, Zha Y, et al. 2009. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lake:The case of Taihu lake,China[J]. Remote Sensing of Environment, 113(6) : 1175–1182. DOI:10.1016/j.rse.2009.02.005 |
| [${referVo.labelOrder}] | Lee Z P, Lance V P, Shang S L, et al. 2011. An assessment of optical properties and primary production derived from remote sensing in the southern ocean (SO GasEx)[J]. Journal of Geophysical Research:Oceans, 116 . DOI:10.1029/2010JC006747 |
| [${referVo.labelOrder}] | 李莉, 尹球, 巩彩兰, 等. 2011. 太湖不同叶绿素a浓度水体荧光特征分析[J]. 光谱学与光谱分析, 2011, 31(1) : 136–140. |
| [${referVo.labelOrder}] | 李俊生, 张兵, 陈正超, 等. 2006. MODIS数据辅助中巴资源卫星图像大气校正研究[J]. 中国科学, 2006, 36(增刊) : 141–150. |
| [${referVo.labelOrder}] | 李云亮, 张运林, 李俊生, 等. 2009. 不同方法估算太湖叶绿素a浓度对比研究[J]. 环境科学, 2009, 30(3) : 680–686. |
| [${referVo.labelOrder}] | 李素菊, 吴倩, 王学军, 等. 2002. 巢湖浮游植物叶绿素含量与反射光谱特征的关系[J]. 湖泊科学, 2002, 14(3) : 228–234. |
| [${referVo.labelOrder}] | Luoheng H, Donald C, Rundquitst D C. 1997. Comparison NIR/RED ratio and first derivative of reflectance in estimating algal-chlorophyll concentration:a case study in a tubid reservoir[J]. Remote Sensing of Environment, 62(3) : 253–261. DOI:10.1016/S0034-4257(97)00106-5 |
| [${referVo.labelOrder}] | Mishra S, Mishra D R. 2011. Normalized difference chlorophyll index:A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters[J]. Remote Sensing of Environment . |
| [${referVo.labelOrder}] | 马万栋, 王桥, 吴传庆, 等. 2014. 基于反射峰面积的水体叶绿素遥感反演模拟研究[J]. 地球信息科学学报, 2014, 16(6) : 965–970. |
| [${referVo.labelOrder}] | 秦伯强, 胡维平, 陈伟民, 等. 2004. 太湖水环境演化过程与机理[M]. 北京: 科学出版社. |
| [${referVo.labelOrder}] | Richard W, Gould J, Robert A, et al. 1990. Spectral dependence of the scattering coefficient in case 1 and case 2 waters[J]. Applied Optics, 29(3) : 897–1900. |
| [${referVo.labelOrder}] | Rundquitst D C, Han L, Schalles J F, et al. 1996. Remote measurement of algal chlorophyll in surface waters:The case for the first derivative of reflectance near 690 nm[J]. Photogrammetric Engineering and Remote Sensing, 62(2) : 195–200. |
| [${referVo.labelOrder}] | Schmeltz M, Froidefond J M, Jourdin F, et al. 2010. Remote sensing reflectance reconstruction to obtain water optical properties from MERIS multi-spectral satellite images[J]. Remote Sensing of the Coastal Ocean,Land,and Atmosphere Environment, 7858 : 1–10. |
| [${referVo.labelOrder}] | 石光明, 王晓甜, 张梨, 等. 2008. 基于方向滤波器消除遥感图像孤立条带噪声方法[J]. 红外与毫米波学报, 2008, 27(3) : 214–218. |
| [${referVo.labelOrder}] | 孙德勇, 周晓宇, 李云梅, 等. 2013. 基于光学分类的太湖水体叶绿素a浓度高光谱遥感[J]. 环境科学, 2013, 34(8) : 3002–3009. |
| [${referVo.labelOrder}] | 檀静.2013.面向内陆浑浊水体遥感的Gordon大气校正算法改进方法研究一以太湖为例[D].南京:南京师范大学 |
| [${referVo.labelOrder}] | 唐军武.1999.海洋光学特性模拟与遥感模型[D].北京:中国科学院遥感应用研究所 |
| [${referVo.labelOrder}] | 唐军武, 马超飞. 2005. CBERS-02卫星CCD相机资料定量化反演水体成分初探[J]. 中国科学, 2005, 35(增刊Ⅰ) : 156–170. |
| [${referVo.labelOrder}] | 唐军武, 田国良, 汪小勇, 等. 2004. 水体光谱测量与分析Ⅰ:水面以上测量法[J]. 遥感学报, 2004, 8(1) : 37–44. |
| [${referVo.labelOrder}] | 童庆禧, 张兵, 郑芬兰. 2008. 高光谱遥感原理、技术与应用[M]. 北京: 高等教育出版社. |
| [${referVo.labelOrder}] | Vos W L,Doneze M,Bueteveld H.1986.On the reflectance spectrum of algae in water:the nature of the peak at 700 nm and its shift with varying concentration[R].Communication on Sanitary Engineering and Water Management.Delft |
| [${referVo.labelOrder}] | 王金梁, 秦其明, 李军, 等. 2014. 基于高光谱数据的水体叶绿素a指数反演模型的建立[J]. 农业工程学报, 2014, 30(3) : 128–134. |
| [${referVo.labelOrder}] | Wang M, Gordon H R. 1994. A simple moderate accurate atmospheric correction algorithm for SeaWiFS[J]. Remote Sensing of Environment, 50(3) : 231–239. DOI:10.1016/0034-4257(94)90073-6 |
| [${referVo.labelOrder}] | 王海君.2007.太湖水色遥感大气校正方法研究[D].南京:南京师范大学 |
| [${referVo.labelOrder}] | 杨煜, 李云梅, 王桥, 等. 2009. 富营养化的太湖水体叶绿素a浓度模型反演[J]. 地球信息科学学报, 2009, 11(5) : 597–603. |
| [${referVo.labelOrder}] | Yacobi Y Z, Gitelson A, Mayo A. 1995. Remote sensing of chlorophyll in Lake Kinnerert using high spectral resolution radiometer and landsat TM:Spectral features of reflectance and algorithm development[J]. Journal of Plankton Research, 17(11) : 2155–2173. DOI:10.1093/plankt/17.11.2155 |
 2017, Vol. 37
2017, Vol. 37