2. 湖北工业大学资源与环境学院, 武汉 430068;
3. 湖南省洞庭湖水利工程管理局, 长沙 410000
2. College of Resources and Environment, Hubei University of Technology, Wuhan 430068;
3. Dongting Lake Water Resources Administration Bureau of Hunan Province, Changsha 410000
水华是一种受水动力、生物化学过程影响的复杂水环境污染现象, 因其暴发迅速, 作用范围广, 严重污染水质而受到广泛关注.近20年来, 国内外已有不少关于水华预测方法的相关研究, 如Recknage早在1997年就将人工神经网络用于对藻类细胞规模、藻种演替和水华持续时间的预测(Recknagel et al., 1997), 并证明该方法能够有效鉴定出动态水体环境中的主要驱动因子.Marsil通过一定时间段内的观测数据构建相关因子模糊曲线, 根据曲线的昼夜波动变化和统计分布规律, 对水华做出定性预测(Marsil, 2004).Chen分别利用delft3D数值模块和元胞自动机方法计算非生物环境和叶绿素a浓度, 并将该方法与传统BloomⅡ模型进行对比(Chen et al., 2006), 取得较好的预测结果.Park在研究Juam和Yeongsan水库水环境问题时, 将人工神经网络和支持向量机两种机器学习算法用于叶绿素a浓度的预测, 结果表明支持向量机无论是在准确度还是水华机制描述方面均优于人工神经网络(Park et al., 2015), 上述方法对一般水体环境具有较好的适用性, 并取得一定成效;对于三峡水库水动力背景复杂的水体环境(纪道斌等, 2010b), 国内部分学者从营养盐补给, 点面源污染, 倒灌异重流及浮游生物调查统计等多方面入手, 进行深入的研究和总结, 探讨水华暴发机理及其影响因素, 采用水动力背景下水华生消机理分析与水质模型模拟相结合的方法进行防控, 对水华暴发提出合理的预警与调控策略(杨正健, 2014).
然而, 三峡水库支流库湾存在明显的干支流水体参混和水温分层特性(刘流等, 2012), 水华暴发机理的复杂性(曹巧丽等, 2008;苏妍妹等, 2008;杨敏等, 2014;杨正健等, 2008;张晟等, 2008)以及二者之间响应关系的不确定性, 导致现阶段采用基于复杂的数值模型预测方法和从机理角度对水华进行模拟和预测, 不仅需要进行大量繁冗的数学计算, 过度依赖数据量与经验公式, 而且复杂的水动力背景可能导致模拟结果滞后(诸葛亦斯等, 2009), 同时水文、水质观测数据的完整性和有效性在一定程度上限制了该类预测方法的应用.目前, 三峡库区支流库湾回水区水华暴发频繁, 水质污染严重, 而水质模型以及统计学模型均存在地域适用性或数据量要求等诸多限制, 因此, 在数据信息不完整的条件下, 选用简单易行、充分挖掘有限数据且精度较高的灰色系统分析法能够较合理地对水华作出短期定量预测.目前在水质预测中应用较为广泛的是GM(1, 1) 预测模型及其相应的修正模型, 如灰色动态模型群方法(李如忠, 2003)、残差修正(王开章等, 2002), 马尔科夫链修正(于慧等, 2014;赵琳琳, 2007;邹志红, 2009), 灰色滚动模型(Chang et al., 2005)等, 上述方法具有一定成效, 但对于波动序列的适应仍有待改进.本文在灰色伯努利模型的基础上, 采用多种方式对模型进行优化, 改善模型对序列波动性(李汉东, 2000)和趋势性的适应度, 提高了模型的抗干扰能力和预测精度, 将该优化模型用于水华预测取得较好的结果.
本研究以2007—2014年的叶绿素-a野外观测数据(见表 1)为依据, 对该时段内数据序列进行模拟和预测, 并根据结果分析预测因子(叶绿素-a浓度)的时空分布特征, 为防控库区支流水华提供参考.
| 表 1 2007—2014年7月XX06点位的叶绿素-a平均浓度 Table 1 Chlorophyll′s average concentration of site XX06 in July during the period of 2007 to 2014 |
非线性灰色伯努利模型(Nonlinear grey Bernoulli model)NGBM(1, 1) 是灰色预测模型GM(1, 1) 的变体, 属于灰色系统理论中的动态序列处理方法.灰色模型主要适用于指数型或幂函数型增长序列, 当数据序列非单调且跳跃性较大时, 需对序列进行光滑性指数和准指数规律检验, 若不满足要求, 可采用滑动平均法对源序列进行预处理, 以削弱个别极端值的影响, 强化整体趋势.NBGM(1, 1) 模型是在传统灰色模型GM(1, 1) 的基础上引入指数指标r, 将原白化微分方程改进成为非线性灰色伯努利指数微分方程, 通过调整r的值可以使方程解的曲率较好地适应原始序列累加操作后的趋势和规律, 提高了模型应用的灵活性和模拟精度.当r=0和r=2时, 该模型分别还原成为GM(1, 1) 模型和灰色Verhulst模型, NGBM模型操作步骤详见文献(Chen, 2008).
2.2 模型优化尽管NGBM(1, 1) 模型在传统GM(1, 1) 模型的基础上有一定的性能改善, 但在处理不同波动程度和无序干扰的原始数据时, 性能表现仍然比较粗糙, 留有较大的优化空间.本文从以下几个方面对模型进行优化:
2.2.1 step-1参数优化在数据预处理阶段, 通过数据变换的方式对原始数据进行一定的数学转换, 使原本毫无规律的初始序列在变换后形成一定的灰指数律, 同时改善序列的光滑度, 保证模型输入数据的有效性.本研究采用指数变换(向跃霖, 1995):
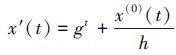
|
(1) |
式中, g, h∈(0, ∞).变换公式中的系数g, h 以及NGBM模型中的背景值p(默认取p=0.5) 和幂指数r为待定参数, 利用遗传算法对上述4个参数进行率定, 灰色滚动模型新陈代谢过程中最佳子序列长度l, 则通过引入评价指标:相对误差比(RPE)以及平均相对误差比(ARPE), 进行比较后确定.

|
(2) |
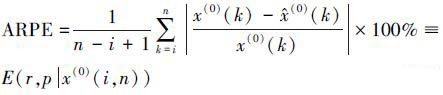
|
(3) |
马尔科夫过程是在后无效条件下、时间和状态均为离散的情况下, 研究某一事件状态与状态之间转移规律的随机过程.马尔科夫过程中, 其概率转移矩阵包含该过程的所有信息, 描绘了系统的迁移过程, 该过程经过有限次转移后, 最终达到平衡状态.系统的最终平衡状态只与概率转移矩阵有关, 而与初始状态无关, 正好与滚动灰色模型新陈代谢的特点相适应.灰色模型的原始序列数据经常受到各种因素的影响而呈现出一定的随机波动性, 如本文中研究的叶绿素-a浓度, 会因水体中其他营养盐的浓度变化、降雨以及上游水库蓄泄等因素而发生改变, 这种影响在模型模拟时通过系统误差表现出来, 从而影响模型的预测精度, 马尔科夫链可以通过概率转移矩阵获取系统状态转移过程的统计特征, 因而可用于灰色模型的随机误差修正.
(1) 确定状态集合由式(2) 可得到第k个数据预测值和真实值之间的相对误差比εk, 其中εk∈I=min(εi), max(εi), 将区间I分成q个同等间隔的状态区间, 每个状态区间为εk∈Ij=Lj, Uj, j=1, 2, ..., q, Lj和Uj分别为状态区间Ij的下限和上限.
(2) 建立状态转移概率矩阵相对误差比的整个状态集合为I, 从当前状态Ii到下一个状态Ij的转移概率为pij, pij可以表示为:
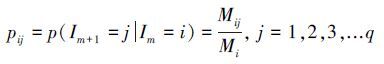
|
(4) |
Mij表示状态i向状态j转移所发生的次数, Mi为相对误差比属于状态i的数据个数.将转移概率pij排列成转移概率矩阵P为:
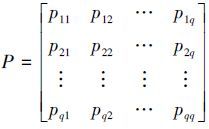
|
(5) |
本文中的系统误差状态转移次数为1次, 故一步转移概率矩阵P即可满足计算要求.
(3) 对预测值进行误差修正修正后的预测值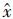
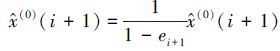
|
(6) |
式中,ei+1=ν(aj(i))T,aj(i)为转移矩阵P 中第j个状态区间的行向量,即aj(i)=(pj1,pj2,...,pjq),v为每个误差状态的代表向量,v=(v1,v2,...,vj,...,vq),vj取值默认为vj=0.5×(Lj+Uj),即使用每个误差状态区间的中心向量作为代表向量对误差进行描述.然而在灰色模型中,这种随机误差属于未知灰色量,中心向量不能完整地表达随机误差的分布信息,因此引入灰色参数向量α来描述整个误差状态区间上随机误差的分布,其中α∈0,1, vj可由式(7)描述:
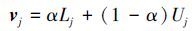
|
(7) |
确定参数p, r, l后, 即可利用模型进行预测计算, 根据式(6) 对预测数据进行误差修正, 修正后的预测值结合式(3) 即可求得长度为l 子序列的预测平均误差:

|
(8) |
以E2为目标函数, 利用遗传算法对α值进行优化, 当E2达到最小值时, α为最优取值.
2.2.3 step-3子序列优化GM滚动模型的新陈代谢过程充分说明, 一次使用序列中所有离散数据建模的效果并不理想, 因为序列中不同时间序数对应的数据对当前预测结果的影响不同, 越靠后的数据, 影响越大, 而且同一序列对未来不同时段的预测精度不同, 预见期越长, 效果越差.所以通过不断更新序列, 以保证预测的准确性.基于上述原因, 我们选择以子序列为建模基础, 模型结构优化过程见图 1.
 |
| 图 1 子序列优化结构图 Fig. 1 Structure chart of subset optimization |
在预测前, 通过模拟计算将每一个子序列和与之相对应的拟合参数匹配, 求解相关的误差标准并作对比, 目的是精确地寻找最佳子序列长度l.当l确定以后, 选择最靠近预测值的前l个数据作为建模数据, 再进行一次子序列独立优化操作, 率定预测所需要的参数, 最后根据模型计算预测值.
3 实例应用(Instance applications)香溪河是三峡水库紧邻坝前湖北库区的最大支流, 河长94 km, 自北向南流经神龙架林区、秭归县和兴山县, 于香溪镇注入长江, 流域面积达3095 km2.受三峡水库蓄水的影响, 与长江交汇的河口至高阳大桥形成回水淹没库湾, 水体由河流水体转变为类湖泊水体.蓄水后, 支流库湾由于受到回水顶托作用导致与长江干流水体交换能力减小, 大量营养物质在库湾富集, 为香溪河库湾藻类生长提供了条件.库湾内春季和夏季连续多次暴发水华, 水体富营养化严重.由于春夏季是水华暴发的敏感时期, 自然水体中当优势藻种稳定时藻密度与叶绿素浓度存在较明显的正相关关系(刘信安等, 2005), 预测时间段内监测的藻密度与水华时长与上述理论基本吻合(部分年份藻密度较高, 水华时长较短, 平均叶绿素浓度反而不高, 详见图 2), 故水体表层叶绿素-a含量的变化在一定程度上反映水华生消变化的趋势, 所以本文采用2007—2014年7月份香溪河流域兴山县水文观测站测量的XX01~XX10点位叶绿素-a平均浓度(CHL)作为研究对象, 分别以2007—2014年夏季观测平均值为输入数据, 模型新陈代谢过程中子序列的模拟结果为校核数据, 2015年预测值为输出及验证数据(更新2015年监测数据可对2016年进行预测输出).
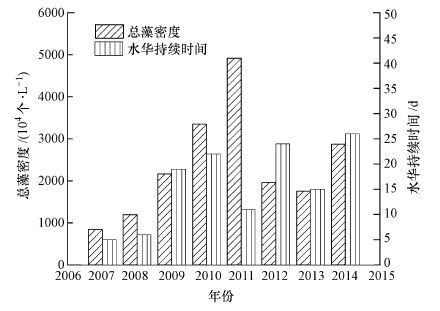 |
| 图 2 7月水华期间总藻密度与水华持续时间 Fig. 2 Density of total algae and water bloom duration in July |
模型中的背景值、指数p, r为模型内关联参数, 序列长度l则是外关联参数, 故分阶段分别对这两部分参数进行率定, 本文分别计算了香溪河上中下游的3个代表点位XX08、XX06和XX02, 以XX06点位数据为例.在第一阶段中, 选取整个序列作为建模数据源并采用指数变换(见公式(1) )的方式对序列进行预处理, 通过遗传算法对g, h, p和r这4个参数优化率定.在优化过程中, 为提高遗传算法的优化性能, 将ARPE与常系数c的乘积作为目标函数, 其中常系数c=1000.具体的优化过程见图 3, 其中X轴为种群进化代数, Y轴为目标函数值, 图中曲线显示, 目标函数值在种群进化至200代以后趋于稳定, 最优个体适应度为37.9790, 即平均相对误差为3.7979%, 对应的参数取值为:g=0.3715, h=104.4100, p=0.2709, r=0.2207.
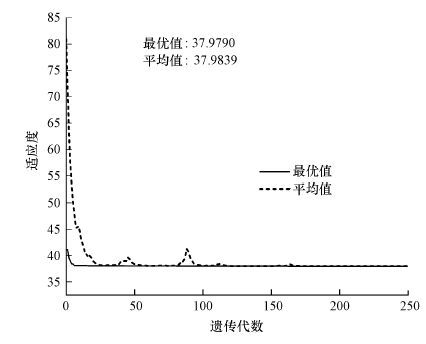 |
| 图 3 遗传算法参数优化过程 Fig. 3 Optimization procedure of parameters with genetic algorithm |
在第二阶段, 分别计算不同长度子序列的拟合误差Ek和预测误差εk, 由极值原理得出最小平均综合误差E1, 确定最优子序列长度.具体结果见表 2.当l=7 时, 子序列的平均综合误差最小, 故最优子序列长度为7, 参数率定完成, 利用模型进行2015年7月叶绿素-a平均浓度的预测, 结果见表 3.
| 表 2 XX06最佳子序列长度l计算过程 Table 2 Calculation process for the optimal length of subsets of XX06 |
| 表 3 XX06点位叶绿素-a浓度(mg·L-1)子序列预测结果 Table 3 Prediction results of chlorophyll′s average concentration for site of XX06 |
根据状态区间确定公式q=fix(ln(l)/ln2) (Imbusch et al., 2000), 求得区间数q=fix(ln7/ln2) =2.由表 3状态区间的划分估计一步转移概率矩阵, 引入灰色参数α后灰色误差区间的表达式为:
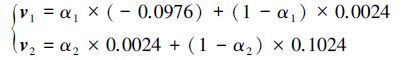
|
由公式(8) 得到对数据实行误差修正所需要优化的目标函数, 通过遗传算法确定灰色参数α的最优取值.优化后的α 取值为α1=0.5367, α2=0.6981, 修正后的结果见表 4.
| 表 4 XX06点位叶绿素-a浓度修正结果 Table 4 Modification results of chlorophyll′s average concentration for site of XX06 |
对各个子序列重新率定参数并通过比较平均综合误差比得到最优子序列长度l′=7, 以源序列后7位元素为建模序列, 再次执行step-1和step-2, 参数优化结果见表 5, 点位的模拟及预测结果见图 4和图 5.
| 表 5 参数率定结果 Table 5 Result of parameters calibration |
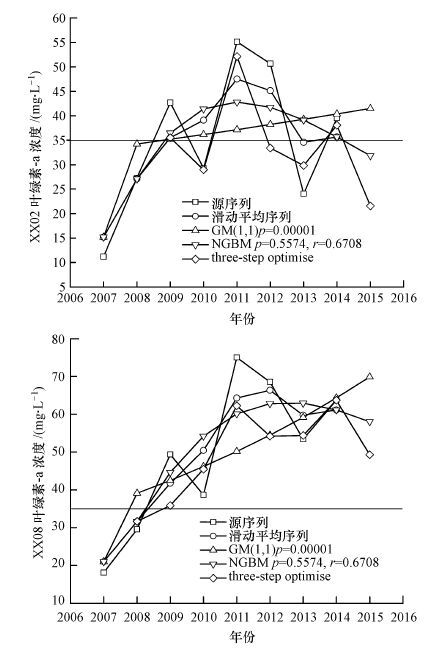 |
| 图 4 XX02和XX08点位模拟预测结果 Fig. 4 Simulation and prediction results of CHL for sites of XX02 and XX08 |
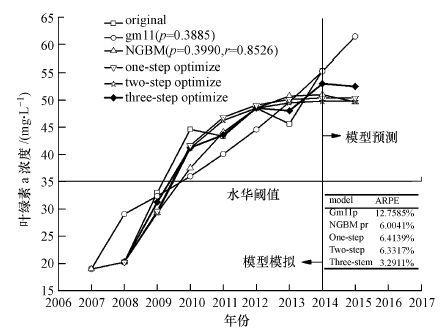 |
| 图 5 XX06不同优化模型的模拟和预测结果对比 Fig. 5 Comparison of simulation and prediction results between different optimized models |
从图 5预测结果来看, 几种模型对XX06点位2015年7月叶绿素-a平均浓度的预测值大部分位于50~55 mg·L-1, 其中三重优化后的模型预测值为52.4386 mg·L-1, 与实际监测值55.0672 mg·L-1最为接近.该点位的叶绿素-a浓度整体上呈上升趋势, 于2011和2013年出现局部下降的现象, 但下降幅度有限, 同时回升趋势较为剧烈, 尤其是2015年叶绿素-a浓度远高于水华阈值35 mg·L-1, 点位附近的水体富营养化严重, 该时段内随时可能暴发水华.靠近上游的XX08点位叶绿素浓度有较明显的起伏波动, 与2014年相比, 2015年叶绿素浓度呈下降趋势, 但仍高于阈值.下游XX02点位叶绿素浓度走势为“几”字型, 在水华阈值附近上下浮动, 存在一定的水华暴发风险.
从各模型的拟合效果来看, 传统的GM(1, 1) p模型拟合结果和源数据偏差较大, 而且几乎完全不能适应源序列的波动性和随机性, NGBM模型在模型拟合精度上有一定的提升, 但该模型对数据波动性反映较为迟钝.经过参数率定后的one-step优化模型以及two-step误差修正模型已经能够在一定程度满足拟合精度的需要, 并且开始适应数据波动.对每个子序列独立优化后, 拟合效果有很大改善, 尤其是在数据波动趋势方面的适应表现突出(见图 4), 与源序列曲线走势基本吻合.
根据香溪河其他点位数据应用上文中优化模型进行预测, 预测结果详见图 6.
 |
| 图 6 2015年7月香溪河XX00~XX10点位叶绿素-a浓度分布 Fig. 6 Distribution of chlorophyll′s average concentration in July 2015 for sites of XX00~XX10 |
1) 在模型参数率定过程中, 未考虑子序列独立优化的条件下, 子序列的参数确定是按照参数继承的方式从源序列模型中获得.图 5中, 继承源序列率定参数的子序列在进行两步优化后, 平均相对误差6.3317%仍大于NGBM(p, r)源序列模型的6.0014%, 这种现象源于继承参数不能和子序列相匹配.尽管源序列建模已具有较好的精度, 但NGBM(p, r)模型仅考虑到拟合精度, 忽略源序列内部的预测精度, 故曲线前期拟合良好, 后期不适应序列波动, 抗干扰性差, 预测值相对于源序列的残差序列均方差较大.
当选用不同的子序列进行拟合、预测时, 各序列之间由于建模基础和数据长度不同, 继承源序列参数的模型性能表现各异.单一离散数据的差异或增减, 均在一定程度上影响模型的最终预测结果.为避免这部分系统误差, 需要对各子序列分别匹配参数即独立优化.图 7为未进行误差修正的情况下, 继承源序列参数和子序列独立优化的对比.
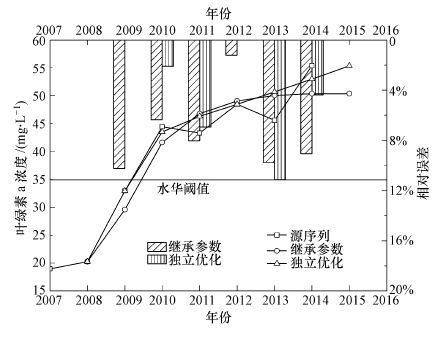 |
| 图 7 子序列独立优化前后对比图 Fig. 7 Comparison of prediction results for XX06 before and after subset independent optimization |
由图 7可知, 独立优化的模型模拟效果有明显的提升, 其大部分拟合数据相对误差小于直接继承参数的情况, 甚至部分离散数据与源序列数据完全吻合, 就整体趋势而言, 其无法反映源序列的波动性.综合图 5和图 7对比可知, 模型参数是影响模型性能的相关因素, 误差修正则是影响模型适应能力的相关因素.
合理地选取子序列进行预测, 能够同时兼顾拟合误差以及预测误差, 有效提升模型的预测精度, 但随着源序列数据的增加, 子序列的长度以及相同长度子序列的个数会发生动态变化.在源数据量微薄的情况下, 子序列长度越长, 可供参考的同等长度子序列个数越少, 反映源序列内在规律的信息量越少, 从而影响子序列最优长度的确定.其次, 本模型未输入营养盐、水动力等相关数据, 而是将其笼统地视为随机灰色量, 以随机误差的形式表现其对整体趋势的影响, 故在长期预测和机理研究方面精度受限, 上述不足会在今后的研究中加以改善.
2) 水华的形成是受多因素影响的复杂生态过程, 营养盐补给的改变、水温变化、水面升降、点面源污染、风速风向改变、流速变化以及水体交换等均对叶绿素-a浓度造成较大影响.图 6中, 源头水体长期处于流量、流速均较大的状态, 营养盐积累较少;长江干流和干支流相接处的水体由于受到倒灌异重流和上游顺坡异重流(纪道斌等, 2010a)的影响, 干支流水体交换频繁, 同时流速较大, 蓄泄水期间稳定系数低(李媛等, 2012), 不利于营养盐的沉积, 故其附近的点位叶绿素-a浓度一直维持较低的水平, 变化较小.因此, 灰色模型能够较好地分析模拟数据序列的变化规律, 预测结果和观测值相近.库湾中上游XX05~XX09点位区域夏季明显的垂向水温分层, 导致水体稳定度增加(易仲强等, 2009)以及水体混合层深度突然减小(刘流等, 2012), 促进水华的频繁暴发和叶绿素-a浓度的剧烈波动, 同时附近磷矿点源污染, 夏季降雨, 干流倒灌对中上游的营养盐补给(操满等, 2015), 水库蓄泄导致的水面涨落以及次级支流汇流等因素导致该区域叶绿素-a浓度变化具有较大的不确定性, 且该处源序列数据的无序性和波动性对灰色模型建模有很大影响, 在忽略其他因素影响的情况下, 有限的数学关联得到的预测结果误差较大.次级支流交汇处如XX08, 流量流速增加导致叶绿素-a浓度有所降低, 同样位于支流交汇处的XX05, 由于受到XX08~XX06高浓度连续区域的边缘扩散影响, 叶绿素-a浓度整体反而有所上升, 不确定因素和空间异质性是灰色模型在预测时产生较大误差的部分原因.XX02点位较实测叶绿素浓度较高可能源于异重流类型为中下层倒灌异重流或异重流潜入距离不够, 未能打破水体分层状态.
3) 优化模型基本能够反映2015年香溪河库湾回水区水华易暴发区域分布, 即河口靠近上游方向的局部次危险区(XX02) 和中上游连续高危区(XX05~XX08) , 故可作为评估水华的参考方法, 同时建议相关部门加强相应点位区域的水环境样点监测, 防患于未然.
5 结论(Conclusions)1) 本文将多重优化理论引入灰色伯努利模型, 验证模型的优化效果, 马尔科夫修正与子序列独立优化的使用, 结合遗传算法的全局参数优化, 显著增强了该模型预测的准确性和对波动序列的适应性, 其中模型参数是影响模型性能的相关因素, 误差修正则是影响模型适应能力的相关因素.
2) 利用该模型对叶绿素-a浓度序列作出短期预测, 预测结果表明该模型能够较好地反映香溪河近几年夏季叶绿素-a平均浓度变化趋势以及已有数据与预测数据之间的非线性关系;流速变化、降雨等不确定因素和空间异质性是模型预测产生较大误差的部分原因.
3) 河口靠近上游方向的XX02点位为水华暴发局部次危险区, 中上游XX05~XX08区域为连续高危区, 以上区域应作为水华重点监测与防控对象.
| [${referVo.labelOrder}] | Chang S C, Lai H C, Yu H C. 2005. A variable P value rolling Grey forecasting model for Taiwan semiconductor industry production[J]. Technological Forecasting and Social Change, 72(5) : 623–640. DOI:10.1016/j.techfore.2003.09.002 |
| [${referVo.labelOrder}] | Chen C I. 2008. Application of the novel nonlinear grey Bernoulli model for forecasting unemployment rate[J]. Chaos, Solitons & Fractals, 37(1) : 278–287. |
| [${referVo.labelOrder}] | Chen C I. 2008. Forecasting of foreign exchange rates of Taiwan's major trading partners by novel nonlinear Grey Bernoulli model NGBM(1,1)[J]. Communications in Nonlinear Science and Numerical Simulation, 13(6) : 1194–1204. DOI:10.1016/j.cnsns.2006.08.008 |
| [${referVo.labelOrder}] | Chen Q, Mynett A E. 2006. Modelling algal blooms in the Dutch coastal waters by integrated numerical and fuzzy cellular automata approaches[J]. Ecological Modelling, 199(1) : 73–81. DOI:10.1016/j.ecolmodel.2006.06.014 |
| [${referVo.labelOrder}] | 操满, 傅家楠, 周子然, 等. 2015. 三峡库区典型干-支流相互作用过程中的营养盐交换:以梅溪河为例[J]. 环境科学, 2015, 36(4) : 1293–1300. |
| [${referVo.labelOrder}] | 曹巧丽, 黄钰玲, 陈明曦. 2008. 水动力条件下蓝藻水华生消的模拟实验研究与探讨[J]. 人民珠江, 2008(4) : 8–10,13. |
| [${referVo.labelOrder}] | Imbusch G, Yen W. 2000. The McCumber and sturge formula[J]. Journal of Luminescence, 85(4) : 177–179. DOI:10.1016/S0022-2313(99)00184-2 |
| [${referVo.labelOrder}] | 纪道斌, 刘德富, 杨正健, 等. 2010a. 三峡水库香溪河库湾水动力特性分析[J]. 中国科学:物理学 力学 天文学, 2010a, 40(1) : 101–112. |
| [${referVo.labelOrder}] | 纪道斌, 刘德富, 杨正健, 等. 2010b. 汛末蓄水期香溪河库湾倒灌异重流现象及其对水华的影响[J]. 水利学报, 2010b, 41(6) : 691–696. |
| [${referVo.labelOrder}] | Marsili-Libelli S. 2004. Fuzzy prediction of the algal blooms in the Orbetello lagoon[J]. Environmental Modelling & Software, 19(9) : 799–808. |
| [${referVo.labelOrder}] | 李汉东. 2000. 多变量时间序列波动持续性研究[D]. 天津:天津大学 |
| [${referVo.labelOrder}] | 李如忠, 王超. 2003. 灰色动态模型群法在河流水质预测中的应用初探[J]. 中国农村水利水电, 2003(1) : 76–78. |
| [${referVo.labelOrder}] | 李媛, 刘德富, 孔松, 等. 2012. 三峡水库蓄泄水过程对香溪河库湾水华影响的对比分析[J]. 环境科学学报, 2012, 32(8) : 1882–1893. |
| [${referVo.labelOrder}] | 刘流, 刘德富, 肖尚斌, 等. 2012. 水温分层对三峡水库香溪河库湾春季水华的影响[J]. 环境科学, 2012, 33(9) : 3046–3050. |
| [${referVo.labelOrder}] | 刘信安, 湛敏, 马艳娥, 等. 2005. 三峡库区流域藻类生长与营养盐吸收关系[J]. 环境科学, 2005, 26(4) : 95–99. |
| [${referVo.labelOrder}] | Park Y, Cho K H, Park J, et al. 2015. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservoirs, Korea[J]. Science of the Total Environment, 502 : 31–41. DOI:10.1016/j.scitotenv.2014.09.005 |
| [${referVo.labelOrder}] | 苏妍妹, 纪道斌, 刘德富. 2008. 三峡水库蓄水期间香溪河库湾营养盐动态特征研究[J]. 科技导报, 2008, 26(17) : 62–69. |
| [${referVo.labelOrder}] | Recknagel F, French M, Harkonen P, et al. 1997. Artificial neural network approach for modelling and prediction of algal blooms[J]. Ecological Modelling, 96(1) : 11–28. |
| [${referVo.labelOrder}] | 王开章, 刘福胜, 孙鸣. 2002. 灰色模型在大武水源地水质预测中的应用[J]. 山东农业大学学报(自然科学版), 2002, 33(1) : 66–71. |
| [${referVo.labelOrder}] | 向跃霖. 1995. 废气排放量灰色建模新法初探[J]. 环境科学研究, 1995, 8(6) : 45–48. |
| [${referVo.labelOrder}] | 杨敏, 张晟, 胡征宇. 2014. 三峡水库香溪河库湾蓝藻水华暴发特性及成因探析[J]. 湖泊科学, 2014, 26(3) : 371–378. |
| [${referVo.labelOrder}] | 杨正健. 2014. 分层异重流背景下三峡水库典型支流水华生消机理及其调控[D]. 武汉:武汉大学 |
| [${referVo.labelOrder}] | 杨正健, 徐耀阳, 纪道斌, 等. 2008. 香溪河库湾春季影响叶绿素-aa的环境因子[J]. 人民长江, 2008, 39(15) : 33–35. |
| [${referVo.labelOrder}] | 易仲强, 刘德富, 杨正健, 等. 2009. 三峡水库香溪河库湾水温结构及其对春季水华的影响[J]. 水生态学杂志, 2009(5) : 6–11. |
| [${referVo.labelOrder}] | 于慧, 孙宝盛, 李亚楠, 等. 2014. 应用灰色模糊马尔科夫链预测海河水质变化趋势[J]. 中国环境科学, 2014, 34(03) : 810–816. |
| [${referVo.labelOrder}] | 张晟, 李崇明, 付永川, 等. 2008. 三峡水库成库后支流库湾营养状态及营养盐输出[J]. 环境科学, 2008, 29(1) : 7–12. |
| [${referVo.labelOrder}] | 赵琳琳, 夏乐天. 2007. 灰色马尔可夫链模型的改进及其应用[J]. 河海大学学报(自然科学版), 2007, 35(4) : 487–490. |
| [${referVo.labelOrder}] | 诸葛亦斯, 欧阳丽, 纪道斌, 等. 2009. 三峡水库香溪河库湾水华生消的数值模拟分析[J]. 中国农村水利水电, 2009(5) : 18–22. |
| [${referVo.labelOrder}] | 邹志红, 王乐娟. 2009. 湖泊富营养化趋势的灰色马尔柯夫预测[J]. 环境科学学报, 2009, 29(2) : 427–432. |
 2017, Vol. 37
2017, Vol. 37


