2. 南京信息工程大学气象灾害预报预警与评估协同创新中心, 中国气象局气溶胶-云-降水重点实验室, 南京 210044;
3. 江苏省环境监测中心, 南京 210036
2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration, Nanjing University of Information Science & Technology, Nanjing 210044;
3. Jiangsu Provincial Environmental Monitoring Center, Nanjing 210036
空气质量模式预报和统计预报常被用在实际预报业务中.模式预报为利用大气动力学数值方法, 综合考虑大气物理化学机制, 定量描述一定区域内大气污染物的变化.主要应用有WRF/Chem, MM5/CMAQ等 (Dennis et al., 1996;Wang et al., 2012).模式预报具有多尺度、开放性等优点, 但主要缺点在于污染物排放源的不确定性大, 计算耗时长.统计预报为利用统计方法筛选出与空气污染浓度相关性较强的气象因子, 再与空气污染浓度建立定量关系.统计预报具有简便经济、良好的预报时效性和准确性等优点, 因而在业务预报中应用广泛.常用的统计方法有回归分析、人工神经网络、遗传算法、支持向量机 (SVM) 等 (Burrow et al., 1995;白晓平等, 2007;Wong et al., 2008;谢永华等, 2015).目前主流的预报方法是空气质量模式与统计方法相结合的动力\|统计预报方法, 该方法不仅可预报未来3~7 d, 而且可预报出重污染等转折天气过程.但是, 大气污染物排放源清单的不确定性以及目前对大气物理化学过程, 尤其是大气边界层过程认识的缺陷, 不可避免地造成动力\|统计预报也存在一定的缺陷.
由于气象及环境数据同时具有多维、多尺度、非平稳等特点, 逐步回归虽原理简单速度快, 但不能反映预报因子和预报对象之间的非线性关系.神经网络相对于回归分析能较好的模拟空气污染物的非线性特征, 因而较多应用于空气污染预报.但神经网络收敛慢、易陷入局部最优和鲁棒性不好等缺点也是限制它进一步发展的原因.遗传算法虽具有良好的全局搜索能力, 但局部优化能力差, 算法费时, 在实际应用中容易早熟收敛 (彭昱忠等, 2015).支持向量机 (SVM) 可以巧妙解决小样本、高维度、非线性问题, 其遵循结构风险最小化原则.Lu等 (2005)研究说明SVM对大气污染物预测具有较好的推广能力.Ortiz Garcia等 (2010)使用SVM对马德里市的O3浓度进行预测, 结果表明SVM预报性能优于BP-NN.气象条件对大气污染物的传输、扩散、转化及沉降具有重要作用.周丽等 (2003)研究考虑了同期气象要素对污染物浓度的影响, 部分学者 (王莉莉等, 2011;陈彬彬等, 2012) 增加考虑了前期污染物浓度作为协变量, 何建军等 (2013)考虑了气象要素对污染物浓度影响有滞后性, 均取得了不错的预报效果.但预报时并未同时考虑前期污染物浓度和气象要素的动态影响.当预报因子过多时, 将所有预报因子选入预报模型则容易造成信息冗余.程兴宏等 (2015)选取通过相关性显著性检验的因子作为预报模型的协变量.Juhos等 (2008)通过主成分分析对SVM构建的协变量进行降维.针对目前空气质量预报方法存在的主要缺陷, 本研究提出距离相关系数 (DC) 和支持向量机回归 (SVR) 相结合的统计预报方案DC-SVR.
本研究首先考虑污染物数据和气象要素数据都是时间序列数据, 在选入预报当日气象要素的基础上, 增加选取前期污染物浓度和气象要素作为预报因子.即采用预报日前7 d的PM2.5浓度逐日实测值和气象要素 (风速、风向、日照时数、气压、气温、相对湿度和降水量) 逐日观测值以及预报当日的气象要素逐日观测值作为预报因子.其次本研究提出使用距离相关系数选取重要预报因子.距离相关系数不需要任何的模型假设, 且可以描述预报对象和预报因子的任意回归关系, 更具有可解释性.本研究分季节使用距离相关系数对预报因子进行降维, 按数值大到小进行排序, 选取前9个变量作为重要预报因子集合.最后使用SVR对污染物浓度 (以PM2.5为例) 进行滚动预报.即选取预报日前c d的PM2.5浓度逐日实测值和重要预报因子集合的逐日实测值作为训练集, 使用SVR对预报日的PM2.5浓度值进行滚动预报.其中四季c分别为15、7、10和10.本研究基于SVR使用距离相关系数刻画大气污染物浓度与预报因子间复杂的关系, 为空气质量预报提供一种参考模型.
2 资料和方法 (Datas and methods) 2.1 研究资料本研究使用的资料包括淮安市5个污染观测站点的观测资料和常规地面气象观测资料.资料时间为2013年1月1日—2013年12月31日.大气污染资料由江苏省环保厅提供, 数据为淮安市5个观测站点 (盱眙、洪泽、涟水、楚州和金湖) 监测的PM2.5逐日实测数据, 使用该5个站点的算术平均值代表淮安地区的污染状况.对个别缺失数据, 本研究用k邻近算法来补充.地面气象因子由国家气象信息中心 (http://data.cma.cn/data/online.html) 提供, 分别为风速 (m·s-1)、最大风速的风向 (方位)、日照时数 (h)、气压 (hPa)、气温 (℃)、相对湿度 (%) 和降水量 (mm) 的实测日均值 (降水量为累计值).
2.2 研究方法DC-SVR统计预报模型程序使用Matlab软件编写, 应用libSVM程序包进行SVR训练和预测.DC-SVR试预报模型对PM2.5的预测主要分为以下步骤:①获取大气污染物观测数据和气象数据, 鉴于大气污染物和气象要素数据是时间序列数据, 选择历史天数参数a, 建立样本数据库;②提取预报日PM2.5浓度数据为模型的响应变量 (预报对象), 其它数据 (预报日气象要素值、前期气象要素值和污染物浓度值) 作为协变量.分季节使用距离相关系数对协变量进行降维, 参考最优截断值参数b=[(N/logxN)4/5], 其中N为样本量个数, [·]表示取整.将距离相关系数从大到小排序, 选出前b个协变量作为预报因子集合, 从而优化样本集;③将数据集分为训练集和测试集.在训练集通过SVR训练生成预测模型, 通过比较训练集中预测误差的大小选取最佳的参数及模型, 最后对测试集进行预测.本研究训练集为预报日前c天的PM2.5浓度逐日实测值和重要预报因子集合的逐日实测值.流程如图 1所示.
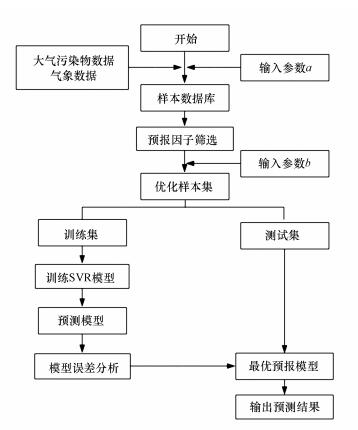 |
| 图 1 DC-SVR预测模型算法流程图 Fig. 1 Diagram of algorithm flow of the DC-SVR forecast model |
在污染物排放源短期少变条件下, 气象要素是影响PM2.5变化的主导因素.本研究在准备预报因子时, 考虑了前期PM2.5浓度值和前期气象条件的动态影响.考虑到影响我国天气系统的典型变化周期 (朱乾根等,2007) 以及Rohde和Muller (2015)对近地面主要大气污染物寿命的研究, 本研究认为前期气象条件和污染物浓度的动态影响天数一般不会超过7 d.最终确定a为7.即在选入预报当日气象要素的基础上, 将预报日前7 d的逐日PM2.5浓度和气象因子选入预报因子.
以2013年淮安市PM2.5浓度日均值预报为例.设第nd为预报日, 预报日前7 d (第n-7至n-1 d) 为起报区间.Yn为预报日PM2.5的预报值.Yj, j=n-7, ..., n-1.为起报区间PM2.5的实测值, Xij, i=1, 2, ..., 7;j=n-7, n-6, ..., n.为第n-7至n d 7种气象要素的观测值共63个预报因子供预报模型筛选, 如表 1所示.
| 表 1 淮安市PM2.5预报模型的预报因子 Table 1 Prediction factors of PM2.5 forecast model in Huaian |
预报因子过多会导致信息冗余和模型的可解释性降低, 因而要对预报因子进行筛选.本研究的思路是衡量各预报因子与PM2.5之间的相关关系, 相关系数越大则认为预报因子对PM2.5的影响越大, 从而将相关系数较大的那些预报因子选进最终的预测模型.常用的相关系数有Pearson相关系数和秩相关系数.传统的Pearson相关系数只能度量两个变量间的线性相关关系, 且必须服从正态分布的假设.秩相关系数虽然度量了更广义的单调关系, 但检验功效降低.本研究首先使用距离相关系数 (DC) 衡量预报因子与PM2.5之间的相关性, 并选取重要预报因子.DC的优点在于可以描述预报对象和预报因子的任意回归关系, 无论它是线性或非线性, 且不需要任何的模型假设和参数条件, 大大加强了该方法的普适性.
本研究使用距离相关系数来衡量两变量u和v的独立性, 记为dcorr (u,v).当dcorr (u,v)=0时, 说明u和v相互独立;dcorr (u,v) 越大, 说明u和v的距离相关性越强.设{(ui,vi), i=1, 2, …,n}是总体 (u,v) 的随机样本, Székely等 (2008)定义两随机变量的u和v的DC样本估计值为
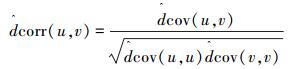
|
(1) |
其中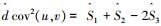

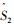
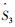
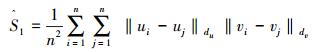
|
(2) |
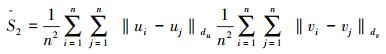
|
(3) |

|
(4) |
同理计算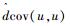

支持向量机 (SVM) 是由Vapnik (1995)提出的一种新型机器学习方法.支持向量机与传统的气象预测方法 (如逐步回归、卡尔曼滤波方法等) 相比有明显的优势, 它不需要模型假设, 且能较好地避免维数过高和过拟合的问题, 具有预测精度高、求解速度快等优点 (Vapnik, 1998).支持向量机回归 (SVR) 的主要思想是:通过非线性转换函数φ将低维空间中的x映射到一个高维特征空间φ(x), 在特征空间中寻求回归线性超平面, 从而解决低维空间中的高度非线性问题.高维特征空间中线性模型构造如下:
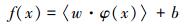
|
(5) |
式中,w是权向量, b是偏置常数, 〈w·φ(x)〉是特征空间的内积.最优超平面回归估计函数转换如下:
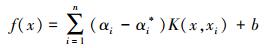
|
(6) |
式中,αi和αi*是拉格朗日乘子, K(x, xi)=〈φ(x)·φ(xi)〉是核函数.本研究选择了高斯径向基 (RBF) 核函数作为SVR的核函数.RBF核函数对非线性系统拟合度较好, 适合大气污染物浓度预测.
3.4 预测效果评估本研究引入以下统计量来评估DC-SVR试预报模型对PM2.5浓度的预报能力, 其中FOR为预报值, OBS为观测值.
① 相关系数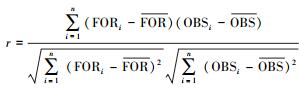
② 平均偏差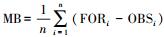
③ 绝对平均偏差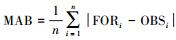
④ 均方根误差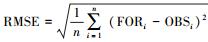
本研究利用DC-SVR滚动统计预报模型进行污染物浓度预报, 距离相关系数能很好地描绘污染物浓度和预报因子间的非线性关系, 可对高维预报因子进行有效地降维, 保留与污染物浓度有很大关联的预报因子.为了防止预测过拟合现象, 本文采用支持向量机回归, 建立非线性系统拟合和预报性能良好的统计预报模型.根据图 1和第3章中的模型方法, 2013年淮安PM2.5日均值预报工作主要分为以下3步.
第1步, 考虑污染物浓度和气象要素的时序相关性, 建立样本数据库, 如表 2所示.
| 表 2 样本数据库 Table 2 Sample database |
第2步, 进行重要预报因子筛选.按季节分别计算预报对象PM2.5浓度和63个预报因子的距离相关系数.距离相关系数越大, 表明该预报因子越重要.对距离相关系数从大到小排序后, 参考阈值标准b=[(N/logN)4/5], 四季N分别为70、85、80和63, b统一确定为9.故各季节分别将前9个预报因子作为重要预报因子集合选入SVR模型.
第3步在选取重要预报因子集合后, 分季节利用SVR对PM2.5浓度进行滚动预报.训练集样本数c的选取参考王茜等 (2015)方法, 并考虑不同训练集样本数在不同季节适用性的差异, 分别选取预报日前c(c取3、5、7、10和15) d的PM2.5浓度逐日实测值和重要预报因子逐日实测值作为训练集, 对预报日的PM2.5浓度值做预报.在预报过程中, 训练集始终为预报日前c d的PM2.5浓度和重要预报因子集合的逐日实测值.当预报日逐日滚动时, 训练集也随之滚动, 以此类推, 进行PM2.5滚动预报.结果显示, 春季前15 d、夏季前7 d, 秋冬季前10 d的PM2.5浓度值和重要预报因子集合的逐日实测值作为训练集预报效果最优.需要指出的是, 由于冬季的数据为2013年1、2和12月的数据, 1月作为训练集需要2012年12月底的数据, 本研究对此时间段不进行预报.故本研究四季的测试集分别为3月23日—5月31日、6月8日—8月31日、9月11日—11月31日、1月18日—2月28日和12月11日—12月31日, 共298 d.
4.2 日平均PM2.5浓度与预报因子的关联性分析图 2是2013年淮安各季节当日PM2.5浓度与63个预报因子的距离相关系数, 图中虚线是选取重要预报因子的距离相关系数临界值, 本研究选取大于等于临界值的因子作为重要预报集合.从图 2可知, 四季预报日PM2.5浓度比前期PM2.5浓度滞后1 d时距离相关系数达到最大值, 分别为0.29、0.67、0.65和0.54, 均达到临界值, 这说明进行PM2.5浓度预报时需考虑前期污染的动态影响.四季日平均PM2.5浓度与气象要素的距离相关系数不是简单地随滞后时间变长而递减的关系, 气象要素对PM2.5浓度的影响有一定的滞后性, 验证了预报时需考虑前期气象要素的动态影响.
 |
| 图 2 2013年淮安各季节当日PM2.5浓度与63个预报因子的距离相关系数 (图中虚线是选取重要预报因子的距离相关系数临界值) Fig. 2 Distance correlation coefficients between 63 predictors and daily averaged PM2.5 concentrations in Huaian during January-December 2013(The dashed lines indicate critical distance correlation coefficients for selecting the important predictors) |
不同季节气象要素的距离相关系数最大值出现的滞后时间不同:春夏秋季除风速和风向外距离相关系数最大值滞后时间在0~3 d内, 冬季除日照时数、降水量和风向外最大值滞后时间在5~6 d内, 较长的滞后时间可能与排放源差异和冬季大气层结较稳定有关.四季日平均PM2.5浓度分别比气温滞后0、2、2、6 d, 其距离相关系数达到最大值, 其中气压和相对湿度与日平均PM2.5浓度的距离相关系数随PM2.5浓度的滞后时间变化趋势与气温较一致.
不同季节气象要素与污染物浓度的距离相关性差异明显:四季选入重要预报因子集合中均含有气温和气压, 气温四季最大距离相关系数分别是0.48、0.53、0.71和0.41, 即秋>夏>春>冬;气压四季最大距离相关系数分别是0.48、0.49、0.69和0.34, 即秋>夏>春>冬.综合分析表明, 气温和气压与PM2.5浓度的距离相关性较其他气象要素好.进一步分析发现, 夏秋冬季只选取了前一日的PM2.5浓度值、前期的气温和气压作为重要预报因子集合.一般认为静稳天气和低风速与PM2.5重污染相关.依据大气动力学理论, 气温和气压是大气热力学和动力学的重要变量, 近地面风速的强弱主要取决于地面气温和气压的变化.因此, 四季选入重要预报因子集合中均含有地面气温和气压.这也体现了近地面大气热力和动力结构变化以及风速的影响.
4.3 DC-SVR预报结果本研究使用SVR对各季节训练集交叉验证后的均方根误差分别为19.61、17.05、30.25和54.85 μg·m-3.表明SVR模型具有良好的稳定性.图 3分别为利用DC-SVR预报模型得到的2013年四季淮安逐日PM2.5浓度预报和实测值的时间序列.由图 3可发现, 淮安季平均PM2.5浓度分别为56.19、48.93、73.39、122.59 μg·m-3, 呈现出春夏 (3—5、6—8月) 低, 秋冬 (9—11、12和1—2月) 高的特征.四季日平均PM2.5浓度大于75 μg · m-3的天数分别占总样本的17%、13%、41%、75%, 即淮安地区秋冬季PM2.5污染呈现浓度高、高浓度时次多的特征.比较分析DC-SVR模型预报和观测PM2.5浓度值, 2013年四季平均偏差仅在±3 μg·m-3之间, 表明DC-SVR试预报具有良好的预测性能.PM2.5浓度预报偏差有明显的季节特征.春夏季分别有77%、75%的天数预报偏差在±20 μg· m-3之间, 秋冬季分别有69%、49%的天数预报偏差在±30 μg· m-3, 春夏秋冬平均绝对误差分别为14.56、15.86、25.43、41.06 μg· m-3, 即秋冬季预报偏差明显大于春夏季.由图 3c和3d可知, 模型对秋冬季部分重污染天气预报的精度相对较差.可能由于样本量较少, 不能覆盖大部分气象条件, 且秋冬季预报因子只选取了前一日的PM2.5浓度值、前期的气温和气压, 当出现特殊天气 (风、雨) 和排放源发生变化 (秸秆燃烧、工业交通) 时, 模型不能捕捉到变化.
 |
| 图 3 2013年淮安各季节逐日PM2.5浓度预报和观测值的时间序列图 Fig. 3 Time series of daily averages of forecasted and observed PM2.5 concentrations in different seasons in Huaian |
图 4给出了2013年淮安逐日PM2.5浓度观测和预报值的散点图.对比各季节PM2.5预测浓度和观测浓度, 二者波动趋势较一致, 相关系数分别为0.45、0.73、0.69和0.57, 均通过了置信度水平为0.01的显著性检验.说明模型对PM2.5逐日变化趋势的捕捉能力夏季>秋季>冬季>春季.春季由于PM2.5浓度均值低、浓度变化剧烈, 相关系数极易受异常值影响, 除去图 4a中一个明显的异常值, 相关系数可达到0.54.总体而言, 本研究所建立的DC\|SVR试预报模型基本能够预报淮安逐日PM2.5浓度的变化趋势, 具有较好的预报精度.
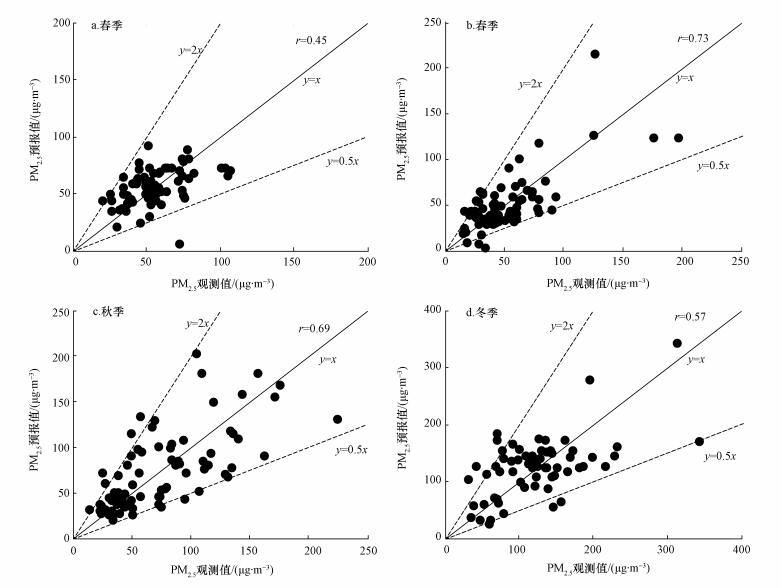 |
| 图 4 2013年淮安各季节逐日PM2.5浓度观测和预报值的散点图 Fig. 4 Scatter plots of daily averages of observed and forecasted PM2.5 concentrations in different seasons in Huaian |
表 3给出了3种统计预报方案.利用相同的资料, 本研究将DC-SVR预测模型与表 3中的3种方案进行对比.表 4给出了2013年淮安4种预报方案下PM2.5浓度预报和实测值的相关系数 (r)、平均偏差 (MB)、绝对平均偏差 (MAE) 和均方根误差 (RMSE).由表 4可知, 除DC-BP外, 其他3种预报方案平均偏差相差不大, 均在±2 μg· m-3之间.DC-SVR预报效果均优于SVR1和SVR2, 其中相关系数、平均绝对误差和均方根误差这3种统计量基于SVR都有一定的优化.这是由于DC-SVR预测模型是在考虑了前期气象要素和污染物浓度的影响并筛选出重要预报因子的基础上利用SVR进行统计预报, 表明距离相关系数筛选出重要信息, 有效地降低了噪声对预测模型的影响;DC-SVR预报效果显著优于DC-BP, 其中各项统计量均优于DC-BP, 改进比为69%, 表明在淮安PM2.5浓度预报中SVR性能优于BP神经网络.
| 表 3 3种预报方案列表 Table 3 3 A list of three forecast methods |
| 表 4 几种预报方案误差统计表 Table 4 Evaluations with different forecast methods |
本研究DC-SVR预报模型预报结果有较好地一致性, 有一定的预报能力.但由于降水量存在大量零值, 直接引用降水量的距离相关系数可能限制其对PM2.5浓度变化的影响.这有待今后进一步完善预报模型中降水量影响因子评估.
5 结论 (Conclusions)1) 在利用支持向量机回归分季节对污染物浓度进行滚动预报的基础上, 本研究建立的DC-SVR空气质量预报模型考虑了前期污染物浓度和气象要素对污染物浓度的动态影响, 并且提出分季节利用距离系数来刻画大气污染物浓度和预报因子之间的非线性关系, 再进行特征筛选, 能有效降低特征维数, 保留影响污染物浓度变化的重要信息.DC-SVR试预报效果在支持向量机回归的基础上有了较大的改进.
2) 本研究尝试将DC-SVR滚动统计预报应用于2013年淮安PM2.5预测.对比全年PM2.5预报和观测浓度之间相关系数高达0.76, 平均偏差仅为1.13 μg · m-3, 平均绝对误差为23.47 μg · m-3. DC-SVR预测精度明显优于3种统计预报方法 (SVR1、SVR2和DC-BP), 表明DC-SVR滚动统计预报模型能更好地预报2013年淮安地区的PM2.5浓度变化.
3) 本研究DC-SVR预报模型仅应用于2013年淮安逐日PM2.5浓度预报, 未来工作可以尝试应用于其他污染物 (PM10, O3, SO2等)、更细的时间尺度 (逐小时) 和更大范围 (省域) 的空气质量统计预报实际业务中.
| [${referVo.labelOrder}] | 白晓平, 张启明, 方栋, 等. 2007. 人工神经网络在苏州空气污染预报中的应用[J]. 科技导报, 2007, 25(3) : 45–49. |
| [${referVo.labelOrder}] | Burrow W R, Benjamin M, Beauchamp S, et al. 1995. CART decision-tree statistical analysis and prediction of summer season maximum surface ozone for the Vancouver, Montreal, and Atlantic Regions of Canada[J]. Journal of Applied Meteorology and Climatology, 34(10) : 1848–1862. |
| [${referVo.labelOrder}] | 陈彬彬, 林长城, 杨凯, 等. 2012. 基于CMAQ模式产品的福州市空气质量预报系统[J]. 中国环境科学, 2012, 32(10) : 1744–1752. DOI:10.3969/j.issn.1000-6923.2012.10.003 |
| [${referVo.labelOrder}] | 程兴宏, 刁志刚, 胡江凯, 等. 2016. 基于CMAQ模式和自适应偏最小二乘回归法的中国地区PM2.5浓度动力——统计预报方法研究[J]. 环境科学学报, 2016, 36(8) : 2771–2783. |
| [${referVo.labelOrder}] | Dennis R, Byun D, Novak J. 1996. The next generation of integrated air quality modeling: EPA's Models-3[J]. Atmospheric Environment, 30(12) : 1925–1938. DOI:10.1016/1352-2310(95)00174-3 |
| [${referVo.labelOrder}] | 何建军, 于晔, 刘娜, 等. 2013. 基于WRF模式的兰州秋冬季大气污染预报模型研究[J]. 气象, 2013, 39(10) : 1293–1303. DOI:10.7519/j.issn.1000-0526.2013.10.007 |
| [${referVo.labelOrder}] | Jubos I, Makra L, Tóth B. 2008. Forecasting of traffic origin NO and NO2 concentrations by Support Vector Machines and neural networks using Principal Component Analysis[J]. Simulation Modelling Practice and Theory, 16(9) : 1488–1502. DOI:10.1016/j.simpat.2008.08.006 |
| [${referVo.labelOrder}] | Lu W Z, Wang W J. 2005. Potential assessment of the'support vector machine' method in forecasting ambient air pollution trends[J]. Chemosphere, 59(5) : 693–701. DOI:10.1016/j.chemosphere.2004.10.032 |
| [${referVo.labelOrder}] | Ortiz Garcia E G, Salcedo Sanz S, Pérez Bellido A M, et al. 2010. Prediction of hourly O3 concentrations using support vector regression algorithms[J]. Atmospheric Environment, 44(35) : 4481–4488. DOI:10.1016/j.atmosenv.2010.07.024 |
| [${referVo.labelOrder}] | 彭昱忠, 王谦, 元昌安, 等. 2015. 数据挖掘技术在气象预报研究中的应用[J]. 干旱气象, 2015, 33(1) : 19–27. |
| [${referVo.labelOrder}] | Rohde R A, Muller R A. 2015. Air Pollution in China: Mapping of Concentrations and Sources[J]. Plos One, 10(8) . DOI:10.1371/journal.pone.0135749 |
| [${referVo.labelOrder}] | Székely G J, Rizzo M L, Bakirov N K. 2008. Measuring and Testing Dependence by Correlation of Distance[J]. The Annals of Statistics, 35(6) : 2769–2794. |
| [${referVo.labelOrder}] | Vapnik V. 1995. The Nature of Statistical Learning Theory[M]. New York: Springer Verlag. |
| [${referVo.labelOrder}] | Vapnik V. 1998. Statistical Learning Theory[M]. New York: John Wiley. |
| [${referVo.labelOrder}] | Wang T, Jiang F, Deng J, et al. 2012. Urban air quality and regional haze weather forecast for Yangtze River Delta region[J]. Atmospheric Environment, 58(15) : 70–83. |
| [${referVo.labelOrder}] | 王莉莉, 王跃思, 吉东生, 等. 2011. 天津滨海新区秋冬季大气污染特征分析[J]. 中国环境科学, 2011, 31(7) : 1077–1086. |
| [${referVo.labelOrder}] | 王茜, 吴剑斌, 林燕芬. 2015. CMAQ模式及其修正技术在上海市PM2.5预报中的应用检验[J]. 环境科学学报, 2015, 35(6) : 1651–1656. |
| [${referVo.labelOrder}] | Wong K Y, Yip C L, Li P W. 2008. Automatic identification of weather systems from numerical weather predication data using genetic algorithm[J]. Expert Systems with Application, 35(1) : 542–555. |
| [${referVo.labelOrder}] | 谢永华, 张鸣敏, 杨乐, 等. 2015. 基于支持向量机回归的城市PM2.5浓度预测[J]. 计算机工程与设计, 2015, 36(11) : 3106–3111. |
| [${referVo.labelOrder}] | 周丽, 徐祥德, 丁国安, 等. 2003. 北京地区气溶胶PM2.5粒子浓度的相关因子及其估算模型[J]. 气象学报, 2003, 61(6) : 761–768. DOI:10.11676/qxxb2003.077 |
| [${referVo.labelOrder}] | 朱乾根, 林锦瑞, 寿绍文, 等. 2007. 天气学原理和方法(第4版)[M]. 北京: 气象出版社: 36–60. |
 2017, Vol. 37
2017, Vol. 37


