2. 中国科学院地理科学与资源研究所, 北京 100101
2. Institute of Geographic Sciences and Natural Resource Research, CAS, Beijing 100101
污染场地修复包括场地调查、风险评估、修复设计、修复工程实施等系列工作.其中, 场地调查是其它工作的数据基础 (廖晓勇等, 2014).场地调查工作完成后, 应建立清晰的场地概念模型, 进行风险评估, 并形成调查评估报告, 为后续修复设计提供支撑.修复决策者再从报告中解析出场地污染物种类、污染范围和水文地质等信息, 为修复工程实施提供科学指导.但由于现阶段我国在场评工作上投入的费用和时间相对较少, 调查报告体现的信息存在不够详尽或不够准确的情况.若在调查工作完成后, 修复决策者在确定修复范围时发现调查采样密度不够, 导致某些区域的边界划定具有不确定性, 这时需要在后期进行补充采样工作.
现有的土壤污染调查布点方法主要包括判断性布点和非判断性布点 (姜成晟等, 2009), 当缺乏场地污染物分布的背景信息, 可采取非判断性采样方法, 如随机采样、均匀网格布点等, 常用于初次摸底采样; 而判断性布点主要根据已有先验知识, 以此设计采样布点方案, 并在潜在的高污染风险区域加大采样密度.污染场地, 特别是工业型污染场地, 具有污染物浓度高, 空间变异性大, 且污染物类型复杂的特点.通常污染区域不大, 但潜在污染土体较深 (廖晓勇等, 2011), 其调查采样的主要是通过地下钻井的方式.这种采样模式具有高成本、样本量较少、空间维度高的特点, 然而用于调查的预算经费有限, 因此在后期进行补充采样时, 应从成本效益的角度出发, 在不降低估计精度的基础上对点位布设进行优化 (Koppe et al., 2011; Soltani et al., 2013; Mark et al., 1988; Hassanipak et al., 2004; Pilger et al., 2001; Mohammadi et al., 2012).应用地统计学方法优化地下勘探钻井点位的布设来提高采样精度已有大量的相关研究报道 (刘庚等, 2013; D′Or D, 2005; Demougeot Renard et al., 2004; Juang et al., 2005; Scheck et al., 1983; Walton et al., 1982; Szidarovszky, 1983).该方法基于钻井数据空间分布的自相关性, 优化调查布点空间布局, 提高调查效率.地统计学诞生于地质、采矿领域, 因而在该领域内的应用比较成熟, 相关研究也较多, 然而在污染场地调查三维钻井方面的研究还较少.早期有学者 (Walton et al., 1982; Journel et al., 1988) 提出使用克里格方差作为测量钻井数据插值结果的不确定性指标, 基于已有的样本点进行Kriging插值, 获取每个未抽样点的Kriging方差, 取具有最大方差的点为需要新插入的样本点, 如此重复多次, 直到样本量达到要求.但同时这些研究中也有强调, 克里格方差在计算时是以全局的方差最小为目标函数, 只考虑采样点的空间几何位置属性 (空间布局), 缺乏对局部变异性的考虑 (Goovaerts, 1997).
本研究基于前期预调查取样的钻井数据的空间位置和污染物浓度值, 从成本效益的角度出发, 拟提出一种对补充采样点位布设优化方法.该方法使用置信度和污染物浓度值两个指标计算最大不确定性值点, 既考虑了采样点的空间几何位置属性, 又考虑到采样点的污染程度信息, 以污染物的浓度值来补足局部变异性.然后基于该最大不确定性点作为确定下一阶段补充采样点位的参考点, 使得新增加的钻井点位能减少研究区总体的不确定性, 实现逼近式动态追补布设点位.最后以某硝基苯类污染场地作为案例验证, 以期为准确估计场地土壤污染物的空间分布和修复污染土方量提供理论支撑.
2 钻井点位布设优化方法 (Optimization method for drilling design)场地土壤污染物的含量是一种区域化变量, 在一定距离内, 各采样点的土壤特性并非完全独立于该样点周边的污染物含量, 而是在空间上表现出一定的相关性.这种相关性可用半方差函数来表示, 其值也反映出污染物含量在空间上的变异性.半方差函数的计算公式如下:
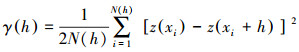
|
(1) |
式中, h为两采样点之间的间距; γ (h) 为h的半方差; N(h) 为距离间隔为h的区域点对个数; z (xi) 为采样点的属性特征值.半方差函数通常采用线性、球形和指数等理论模型进行拟合, 本研究中半方差函数的拟合使用集成到EVS Pro 9.22软件中的专家系统对其最优拟合 (陶欢等, 2014).
克里格插值法是一种加权滑动平均的方法, 对插值点周围的采样点进行加权平均计算待估点的值, 并使其估计方差最小.加权因子和估计方差通过半方差模型计算, 半方差模型描述了输入数据集中所有两两采样点不同距离的差异.根据克里格法的无偏和最优两个条件可以推导出克里格方差的数学表达公式为 (Goovaerts, 1997):
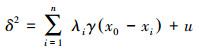
|
(2) |
式中, λi表示克里格的权重, u是拉格朗日乘数, xi为样本区域内任意一点的特征值, γ (x0-xi) 为半方差值.
由于克里格插值是满足二阶平稳假设和内蕴假设的, 若待估点的总体X~N(C, δ2), 则该点置信度的计算公式为:
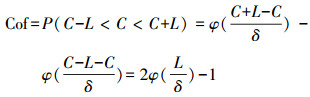
|
(3) |
式中, Cof表示置信度, 指的是估计浓度值落在[C-L, C+L]范围内的可能性大小, C表示研究区某个待估值点的污染物浓度值, L表示用户自定义的置信边界值.在计算估值点的置信度时, 需要估值点的方差 (δ) 和置信边界值 (L) 两个参数.置信边界由用户给定, 每个估值点的克里格方差会在插值过程中自动计算.置信度已经能够对整个收集的样本进行合理的评价, 由于采样点的浓度已知, 所以采样点的置信度最高, 能达到100%, 而采样点稀少的地方, 置信度会越低.通过在置信度较低的区域收集更多的采样点数据, 将会提高对整个场地描述的精度.单独使用置信度并不能更好地计算新增样点的位置, 因为置信度中并未将浓度值考虑进去 (Goovaerts, 1997).
在置信度的基础上加入浓度值指标将会是一种更加成本效益型的增加采样点的方法, 这里将置信度低且预测浓度较高的点称为不确定性最大的点 (Souza et al., 2004), 即下一个新增的采样点.不确定性是一种没有单位的量, 值越低越好, 高的不确定性表示的是对污染物描述较差的可能性很大.低的不确定性表示对未描述的污染物的概率很低.通过EVS Pro软件来计算最大不确定性值, 由于同一阶段研究区的最大不确定性值不止一个, 因而用于计算不确定性的函数在该软件中需作优化处理, 使得新增的采样点数据达到最小, 从而将模型中的最大不确定性点优化到一个.
3 案例研究 (Case study) 3.1 案例区概况案例区地势西高东低、西南高东北低, 呈自西向东、自西南向东北微倾斜.区域属半干旱地区, 主要为暖温大陆性季风型气候.该区四季分明, 多年平均年降雨量573.5 mm, 多年平均蒸发量1692.1 mm, 约是降水量的3倍.场地长150 m, 宽125 m, 深17 m, 东、北邻农田, 南邻河流, 西邻民居, 占地约18750 m2.原厂区内分布有苯胺-2, 5-双磺酸单钠盐、间羟基NN二乙基苯胺、间氨基苯璜酸3类生产车间, 目前车间、仓库等均已被拆除, 东面的硝基苯储罐、北面的办公楼等都均还保留, 厂区东面和南面各有一条排污沟, 东侧有污水池.场地中地下水埋深较浅, 存在着多个含水层, 地质类型按照成因划分为填土层、粉质粘土和砂质粘土, 地质模拟图见图 1.
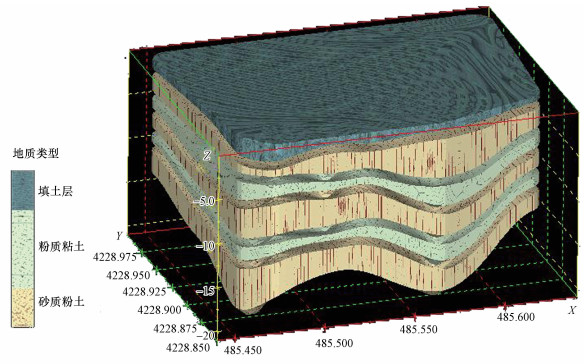 |
| 图 1 研究区地质结构 Fig. 1 Geological structure in the study area |
场地特征污染物为硝基苯, 污染较为单一, 其他污染物的检出超标率较低.硝基苯为芳烃类化合物.作为有机合成中间体及用作生产苯胺的原料, 广泛用于生产染料、香料、炸药等有机合成工业.同时硝基苯是一种潜在的致癌物质, 对人类健康构成严重的威胁, 我国将硝基苯列为“优先控制污染物”.硝基苯由于结构稳定, 比较难降解, 且密度比水大, 难溶于水, 一旦进入水体后可沉入水底或随地下水进入到土壤.厂区土壤中的硝基苯污染主要来自排放含硝基苯的污水, 或是在贮存过程中的意外事故造成的硝基苯泄露.
3.2 采样和分析方法该场地初步布点是以厂区地面的功能区规划为先验知识进行判断布点, 在潜在的高污染风险区域增加采样点.土壤采样区域集中在生产区, 包括间氨基车间、间氨烃生产车间、二五酸车间; 堆放区, 包括废渣堆放点、储罐区以及仓库; 排污区, 主要为东西向排水沟; 控制区, 即厂区四周的边界控制点.共布设了17个钻井点.
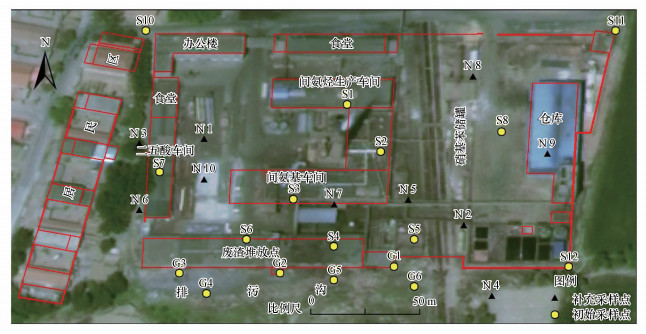 |
| 图 2 土壤采样点分布 Fig. 2 Plot of soil sample sites |
土壤取样按照《土壤环境监测技术规范》执行, 采样过程中去除土壤样品中的碎石等杂质后研磨, 过20目筛, 再装入密封袋, 放入冷冻干燥机中干燥.使用Agilent公司生产的GC-MS检测硝基苯的含量, 测定方法采用USEPA 8270D—2007.土壤样品干重的测定方法采用HJ 613—2011.土壤pH值的测定方法为USEPA 9045D—2004.土壤有机质的测定方法为NY/T 1121.6—2006.
本研究中克里金插值的半方差函数拟合采用集成到EVS Pro 9.22软件中的专家系统对其最优拟合, 然后在软件中建立三维克里格估值模型 (陶欢等, 2014), 三维模型的降维处理采用每口钻井的硝基苯含量的最大值.标量数据使用Excel和SPSS进行处理, 制图软件采用ArcGIS 10.0.
3.3 结果与分析 3.3.1 初步采样结果由于厂区的地下水水位较浅, 整个厂区共采集了样点89个, 场地中的钻井点位的平均深度约为8 m, 钻井最深为G3点和G6点, 16.7 m.从初始钻井的采样数据来看, 土壤中超标最为严重的有机污染物为硝基苯, 钻井S3、S4、S5、S7、S8、G2、G6均有硝基苯含量的检出, 钻井S3、S4、S7、S8的硝基苯主要集中在表土层, 排污沟区的G2、S5、G6在深层有检出.在采集的硝基苯样品中, 其浓度范围为0.001~39.9 mg · kg-1, 平均值为0.75 mg · kg-1, 标准差为4.51, 偏度为7.75, 峰度为65.96, 初始样本采用球状模型拟合最优半方差模型, 得到的变程值51.2 m, 基台值为4.73, 厂区硝基苯的空间分布变异性较大.
土壤理化性质是影响场地特征污染物的吸附能力的重要因素.经取样分析, 土壤样品干重的范围是76%~90%, 平均值为80%.选取场地中4个代表性的样点测得土壤pH分别为7.9、8.4、8.2、8.3, 土壤偏碱性.对应的土壤有机质含量分别为10、8、5.7和4.3 g · kg-1, 土壤有机质含量较低.
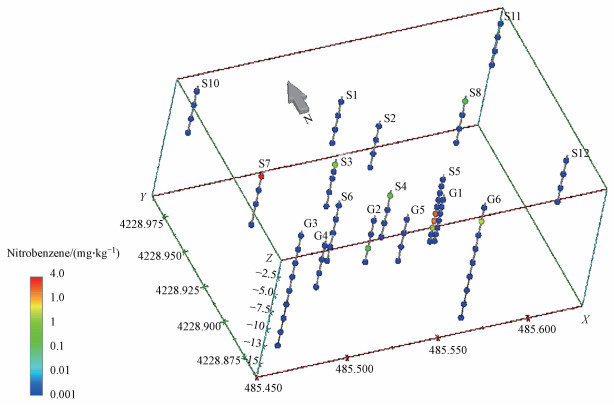 |
| 图 3 三维空间钻井点位分布 Fig. 3 Three-dimensional distribution of drilling points |
为了获得准确的场地硝基苯空间分布信息, 需要在场地初步调查的基础上开展场地详细勘察工作.初步调查旨在识别场地主要污染物及潜在污染区域, 详细勘察是在潜在污染区域增加采样点, 进一步确定污染区的边界及污染程度.在初始样本的基础上, 增加1、10、30、50个点位后, 基台值分别为4.68、3.80、2.56、2.05.在研究区50个样点增加的实验过程中, 整个研究区变程值基本保持稳定, 而基台值则呈指数型减少.补充采样过程中的研究区的不确定性分布图变化如图 4所示.
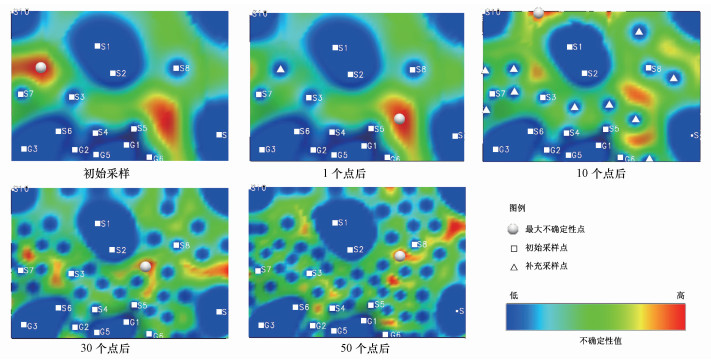 |
| 图 4 补充采样过程中不确定性分布的变化 Fig. 4 Variation of uncertainty distribution in the process of additional sampling |
图 4中可以看出初始采样点附近的不确定性值非常小, 几乎接近于零, 而污染物浓度较高且置信度较低区域的不确定性值较大.在EVS Pro软件中经过全局不确定性优化, 得到全局的最大不确定性值点, 以作为补充采样点.初始采样条件下, 增加1、10、30、50个点的置信度分别为: 47.73%、57.05%、73.80%、82.37%.随着采样点数的增加, 研究区总体的置信度水平有提高.
估算修复污染土方量时的误差主要来源于污染范围被低估和未污染区被高估, 前者会导致场地污染风险不能得到有效地控制, 而过高地估计场地中的未污染土壤会增加不必要的修复费用.最优化的采样方案就是寻找降低污染风险的同时, 确定所需的最佳样本量.由公式 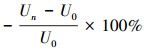
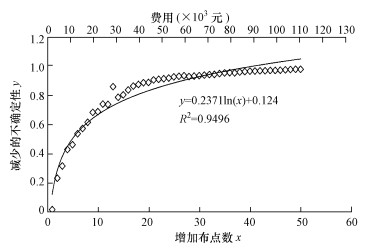 |
| 图 5 增加布点数与减少的不确定性之间的关系 Fig. 5 Relationship between uncertainty reduction and additional sampling |
通过对数拟合减少的不确定性Y和增加布点数X的拟合函数:Y=0.24 In (X)+0.12(R2=0.95).在不考虑钻井样品的运输和化学分析费用等,仅考虑勘探钻井的费用时, 以当前市场价300元· m-1为单价计算钻井的费用, 整个场地的平均深度约为8 m, 因此建1口新的钻井的成本为2400元.结合项目的预算经费和前期采样的实际情况, 希望将不确定性减少至少65%, 于是代入到方程中可计算出需要补充采样点10个方可满足. 10个补充采样点的位置见图 2.
由表 1可见, 在增加10个采样点后, 场地中硝基苯的克里格均值在增加采样点的前后未发生明显变化, 因新增加的采样点的浓度值是初始采样点的半变异函数在该点的估计值, 需要后期在详细勘察的时候实地取样验证.但总体估值方差则由初始的2.899降低到1.743, 降低了40%. 95%置信区间也从±3.34变化到±2.59.同时总体的估计精度提高了22.4%.
| 表 1 克里格方差、置信区间和评价精度的变化 Table 1 Changes of kriging variance, confidence interval, and accuracy |
场地污染物的空间分布受污染源、污染物性质和环境条件等因素的综合影响, 在空间上表现出不同程度的变异性 (刘庚等, 2013).本案例选择的硝基苯类场地属于工业污染场地, 从初步采样结果分析可知, 由于受人类活动的影响较大, 主要受到地面厂房的布局影响, 厂区硝基苯的空间结构变异性较大.从结果中可以看出, 硝基苯的高风险区分布在S7、S3、S4这3个钻井点, 其中S7钻井点的表层硝基苯浓度较高, 其地面建筑物为二五酸车间; S3、S4钻井点的表层出现硝基苯浓度稍高的情况, 其地面建筑均为生产车间.排污沟区的G2、S5、G6在深层有检出, 可能是长期排放的污染废水中的硝基苯下渗的原因.有研究表明 (陈爱辉等, 2013; 宋艳宇等, 2009) 硝基苯在土壤中的迁移转化主要受到pH值和有机质的影响, 文中还指出土壤中硝基苯的吸附量是随着有机质含量的增加而增加, 在酸性条件下, 土壤表面正电荷较多, 吸附量增加.该场地中硝基苯是分布在表层和地下4~9 m的地下水分布层位.研究结果中表明场地土壤pH值偏碱性, 且场地中有机质的含量较少, 土壤对于硝基苯的吸附量较低, 加上场地地下水位较浅, 污染的有机物很可能是由于地下水中硝基苯的上渗.
本研究中使用初始采样点的置信度水平和污染物浓度属性值2个指标作为确定下一阶段补充采样点位的参考, 既考虑了采样点的空间几何位置属性, 又考虑到采样点的污染程度信息, 能够很好地对污染场地中的补充采样点位进行优化.虽然采集样本的污染物浓度属性值参与到各估值点的方差计算中, 但实际上样本污染物浓度属性值的改变并不能影响克里格方差值的变化 (Kim et al., 1981; Armstrong, 1983; Saikia et al., 2006).因此根据克里格方差来决定补充钻井点位缺乏对局部变异性的考虑.大量学者在基于克里格方差补充采样的基础上提出了改进. Yamamoto (1999)使用克里格权重值来定义在自然资源评价中的不确定性, 这种方法中加入置信区间作为数据不确定性的评价. Juang等 (2004)在克里格插值的基础上使用序贯法条件模拟方法 (Sequential Selection), 它是利用前期调查采集的样点得到每个未抽样点的权重, 选取权重最大的点 (权重的计算通常是克里格方差或加权后的克里格方差), 如此重复, 直到由所有样点计算得到的总体精度达到给定水平或新样点不能显著提升总体的精度. 谢云峰等 (2016)和刘庚等 (2013)将污染物含量过渡区作为土壤污染调查结果的不确定性区域, 采用地统计条件模拟, 以土壤污染评价标准为阈值条件, 提出了土壤污染调查补充采样的工作流程和方法.从本研究的结果看, 采用初始采样点的置信度水平和污染物浓度属性值两个指标计算最大不确定性值点, 作为补充采样点位置参考的方法, 在初始样本的基础上, 增加1、10、30、50个点位后, 基台值分别为4.68、3.80、2.56、2.05, 可显著减少空间的基台值.同时置信度分别为: 47.73%、57.05%、73.80%、82.37%, 能显著提高研究区总体的置信度.从图 5中可以得知该方法可以在补充采样初期显著减少总体的不确定性.
Szidarovszky (1983)在他的研究中讨论了采样点位布设补充采样的2种情形:一种是在给定补充采样点个数的情况下, 采样如何布局以使得估计方差达到最小; 另一个是在给定估计方差上限值的情况下, 采样点如何布局使得采样点的数目达到最小.通过拟合模型中不确定性的减少量与采样点之间的函数关系: Y=0.24 In (X)+0.12, 通过钻井的成本, 折算成不确定性的减少与修复成本之间的关系, 结合项目预算经费, 确定补充采样点个数为10个.补充采样点样本量的收集, 受到经济上和地质上的约束.前者建议使用优化标准来获得费用的最大回报.每一个新增的采样点都应该位于对克里格估计的不确定性减少幅度最大的点.从不确定性的减少量与采样点之间的函数关系可以看出, 刚开始增加采样点对整体不确定性的减少程度较大, 随着后期增加的采样点数量的饱和, 继续增加采样点对研究区的不确定性变化影响越来越小, 这与Mcbratney (1983)的研究结果相符.采样点数量确定后, 通过采用置信度和污染物浓度2个指标计算最大不确定性点, 以作为下一阶段点位布局的参考, 不确定性点的计算是在EVS Pro软件中实现.该结果表明实际场地补充采样中并非采集的样本量越多对整体精度的提高越大, 应从成本效益的角度考虑.补充采样的样本量及空间分布对初始样本具有较强的依赖性, 不同的初始样本量和控制位置所得出的最终补充样本会不同, 这是因为补充采样样点的增加是单向, 无法回溯 (姜成晟等, 2009), 因此, 在初始布点时, 样点的分布应尽量地均匀分布在场地中, 从而避免某些区域因采样点稀少, 在补充采样时产生一些不必要的布点.
本研究对比分析了补充采样前后研究区克里格均值、方差和置信区间、估计精度的变化, 结果表明在项目经费的约束条件下, 不确定性减少65%时, 需要补充采样至少10个采样点.补充10个采样点将使得总体估值方差降低了40%, 同时总体的估计精度提高了22.4%, 结果验证了补充采样对场地调查描述精度的提高.研究中的补充采样点位的优化是基于场地中硝基苯污染物浓度值产生, 通常工业污染场地的污染物类型复杂, 单一污染物的场地较为少见 (廖晓勇等, 2011).本研究方法由于受到不确定性值无法绝对定标为某个量纲的限制, 无法对其进行归一化处理, 故而无法将多种污染物的不确定性结合起来确定综合最大不确定性值的位置.另一方面, 多种污染物复合的时候还需要考虑不同污染物的毒性水平, 预测多种污染物的联合毒性 (陈潇霖等, 2016), 下一步研究中可研究如何结合多种污染物的不确定性指标的方法, 以更加精确地确定工业污染场地中的补充采样点的位置.
4 结论 (Conclusions)1) 受地面建筑设施的功能布局影响, 以及含硝基苯的污水排放下渗到土壤、浅层硝基苯污染的地下水中硝基苯上渗到土壤的原因, 使得场地中硝基苯的整体空间结构变异性大.
2) 增加采样点会显著减少空间的基台值, 提高研究区总体的置信度, 同时减少总体的不确定性.且场地补充采样中并非采集的样本量越多对整体精度的提高越大, 应从成本效益的角度考虑.
3) 针对本案例污染场地前期钻井点位的分布, 在项目经费预算的约束条件下, 不确定性减少65%时, 需要至少增加补充采样10个. 10个样点的增加使得总体估值方差降低了40%, 同时总体的估计精度提高了22.4%.表明了使用初始采样点的置信度水平和污染物浓度属性值两个指标作为确定下一阶段补充采样点位的参考, 能够很好地对补充采样进行优化.
| [${referVo.labelOrder}] | Armstrong M. 1983. Comparing drilling patterns for coal reserve assessment[J]. Proceedings of the Australian Institute of Mining and Metallurgy, 288 : 1–15. |
| [${referVo.labelOrder}] | 陈爱辉, 梁慧星, 丁成. 2013. 硝基苯在米草湿地土壤中的吸附特征[J]. 土壤通报, 2013, 44(5) : 1123–1128. |
| [${referVo.labelOrder}] | 陈潇霖, 王学东, 田雨, 等. 2016. 铜、锌对小麦的联合毒性及其预测模型研究[J]. 环境科学学报, 2016, 36(4) : 1493–1499. |
| [${referVo.labelOrder}] | D'Or D. 2005. Towards a real-time multi-phase sampling strategy optimization[M]. Berlin Heidelberg.: Geostatistics for Environmental Applications: 355–356. |
| [${referVo.labelOrder}] | Demougeot Renard H, De F C, Renard P. 2004. Forecasting the number of soil samples required to reduce remediation cost uncertainty[J]. Journal of Environmental Quality, 33(5) : 1694–1702. DOI:10.2134/jeq2004.1694 |
| [${referVo.labelOrder}] | Goovaerts P. 1997. Geostatistics for natural resources evaluation: Applied geostatistics series[M]. New York: Oxford Univ. Press. |
| [${referVo.labelOrder}] | Hassanipak A A. 2004. GET: A Function for Preferential Site Selection of Additional Borehole Drilling[J]. Exploration & Mining Geology, 13(1/4) : 139–146. |
| [${referVo.labelOrder}] | 姜成晟, 王劲峰, 曹志冬. 2009. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3) : 368–380. DOI:10.11821/xb200903012 |
| [${referVo.labelOrder}] | Journel A G. 1988. Nonparametric geostatistics for risk and additional sampling assessment[J]. Principles of Environmental Sampling : 45–72. |
| [${referVo.labelOrder}] | Juang K W, Chen Y S, Lee D Y. 2004. Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils[J]. Environmental Pollution, 127(2) : 229–238. DOI:10.1016/j.envpol.2003.07.001 |
| [${referVo.labelOrder}] | Juang K W, Lee D Y, Teng Y L. 2005. Adaptive sampling based on the cumulative distribution function of order statistics to delineate heavy-metal contaminated soils using kriging[J]. Environmental Pollution, 138(2) : 268–277. DOI:10.1016/j.envpol.2005.04.003 |
| [${referVo.labelOrder}] | Kim Y C, Martino F, Chopra I K. 1981. Application of geostatistics in a coal deposit[J]. Minerals Engineering, 33(10) : 1476–1481. |
| [${referVo.labelOrder}] | Koppe V C, Costa J F C L, Peroni R D L, et al. 2011. Choosing between two kind of sampling patterns using geostatistical simulation: regularly spaced or at high uncertainty locations?[J]. Nonrenewable Resources, 20(20) : 131–142. |
| [${referVo.labelOrder}] | 廖晓勇, 崇忠义, 阎秀兰, 等. 2011. 城市工业污染场地:中国环境修复领域新课题[J]. 环境科学, 2011, 32(2) : 784–794. |
| [${referVo.labelOrder}] | 廖晓勇, 陶欢, 阎秀兰, 等. 2014. 污染场地修复决策支持系统的几个关键问题探讨[J]. 环境科学, 2014, 35(4) : 1576–1585. |
| [${referVo.labelOrder}] | 刘庚, 毕如田, 张朝, 等. 2013. 某焦化场地苯并 (a) 芘污染空间分布范围预测的不确定性分析[J]. 环境科学学报, 2013, 33(2) : 587–593. |
| [${referVo.labelOrder}] | Mark G, Lawrence E A, Geoffrey M. 1988. Application of a new approach for drillholes location optimization[J]. International Journal of Surface Mining Reclamation & Environment, 2(2) : 27–31. |
| [${referVo.labelOrder}] | Mcbratney A B, Webster R. 1983. How many estimations are needed for regional estimation of soil properties?[J]. Soil Science, 135 : 177–183. DOI:10.1097/00010694-198303000-00007 |
| [${referVo.labelOrder}] | Mohammadi S S, Hezarkhani A, Tercan A E. 2012. Optimally locating additional drill holes in three dimensions using grade and simulated annealing[J]. Journal of the Geological Society of India, 80(80) : 700–706. |
| [${referVo.labelOrder}] | Pilger G G, Costa J, Koppe J C. 2001. Additional samples: where they should be located[J]. Natural resources research, 10(3) : 197–207. DOI:10.1023/A:1012517208273 |
| [${referVo.labelOrder}] | Saikia K, Sarkar B C. 2006. Exploration drilling optimisation using geostatistics: a case in Jharia Coalfield, India[J]. Applied Earth Science Imm Transactions, 115(1) : 13–22. DOI:10.1179/174327506X102787 |
| [${referVo.labelOrder}] | Scheck D E, Chou D R. 1983. Optimum locations for exploratory drill holes[J]. Geotechnical & Geological Engineering, 1(1) : 343–355. |
| [${referVo.labelOrder}] | Soltani S, Hezarkhani A. 2013. Proposed algorithm for optimization of directional additional exploratory drill holes and computer coding[J]. Arabian Journal of Geosciences, 6(2) : 455–462. DOI:10.1007/s12517-011-0323-6 |
| [${referVo.labelOrder}] | Souza L E D, Costa J F C L, Koppe J C. 2004. Uncertainty Estimate in Resources Assessment: A Geostatistical Contribution[J]. Natural Resources Research, 13(1) : 1–15. DOI:10.1023/B:NARR.0000023303.03402.c8 |
| [${referVo.labelOrder}] | Szidarovszky F. 1983. Multiobjective observation network design for regionalized variables[J]. Geotechnical & Geological Engineering, 1(4) : 331–342. |
| [${referVo.labelOrder}] | 宋艳宇, 宋长春, 柴俊海, 等. 2009. 湿地土壤对硝基苯的吸附-解吸作用[J]. 环境科学学报, 2009, 29(1) : 140–145. |
| [${referVo.labelOrder}] | 陶欢, 廖晓勇, 阎秀兰, 等. 2014. 某污染场地土壤苯并 (a) 芘含量的三维估值及不确定性分析[J]. 地理研究, 2014, 33(10) : 1857–1865. |
| [${referVo.labelOrder}] | Walton D, Kauffman P W.1982.Some practical considerations in applying geostatistics to coal reserve estimation [C]. Proceeding of the SME-AIME Conference. Dallas: 153-158 |
| [${referVo.labelOrder}] | 谢云峰, 曹云者, 杜晓明, 等. 2016. 土壤污染调查加密布点优化方法构建及验证[J]. 环境科学学报, 2016, 36(3) : 981–989. |
| [${referVo.labelOrder}] | Yamamoto J K. 1999. Quantification of uncertainty in ore-reserve estimation: Applications to chapada Copper deposit, State of Goias, Brazil[J]. Natural Resources Research, 8(2) : 153–163. DOI:10.1023/A:1021894703729 |
 2017, Vol. 37
2017, Vol. 37



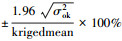 式中, σok2表示的是克里格方差.总体精度变化=(PA0-PA1) / PA0×100%.
式中, σok2表示的是克里格方差.总体精度变化=(PA0-PA1) / PA0×100%.