2. 中国科学院土壤环境与污染修复重点实验室 (南京土壤研究所), 南京 210008;
3. 江苏省水文水资源勘测局扬州分局, 扬州 225002
2. Key Laboratory of Soil Environment and Pollution Remediation, Institute of Soil Science, Chinese Academy of Sciences, Nanjing 210008;
3. Hydrology and Water Resources Survey Bureau of Jiangsu Province, Yangzhou Branch, Yangzhou 225002
纳米材料具有较大的比表面积,能与其他物质充分接触并频繁发生物理和化学反应,在催化、能源、生物医学以及环境修复等领域均有极其广泛的应用 (Mauter et al., 2008;Hendren et al., 2011).纳米氧化石墨烯 (Nano Graphene Oxide, Nano-GO) 作为典型纳米颗粒物,具有独特的物理化学性质,被称为“21世纪最具前景的新型纳米材料”(Chowdhury et al., 2013;Lanphere et al., 2013).在大量生产及应用过程中,纳米颗粒不可避免地进入到环境中,对地下水系统、人类以及其他生物产生不容忽视的影响和潜在的风险 (Dunphy Guzman et al., 2006;Klaine et al., 2008).已有研究表明,纳米颗粒容易吸附并富集土壤和地下水中的有机污染物和重金属等污染物,并作为载体促进其在环境中的迁移 (Lecoanet et al., 2004),造成污染范围不断扩大.因此,研究纳米颗粒在环境中的迁移转化等行为,分析其在土壤和地下水中的归趋,加强对纳米颗粒影响土壤和地下水环境的关注已刻不容缓.
目前,诸多学者对纳米颗粒在多孔介质中的迁移机制与运移行为进行了研究 (Johnson et al., 1996;Bradford et al., 2002;Tufenkji et al., 2005;Tosco et al., 2012),发现其运移行为受到多种物理化学条件的影响.研究表明,纳米颗粒浓度降低、粒径增大及介质中渗流速度减小均会抑制其在饱和多孔介质中的运移 (Lecoanet et al., 2004;Wang et al., 2012);离子强度减小有利于纳米颗粒迁移 (孙慧敏等,2012a);当纳米颗粒表面为可变电荷,且表面电位与石英砂表面电位同符号时,环境中pH增加促进纳米颗粒运移 (孙慧敏等,2012b).现有研究普遍仅考虑均质饱和或非饱和多孔介质中纳米颗粒运移的规律 (Lenhart et al., 2002;Tian et al., 2010;Godinez et al., 2011;Fang et al., 2013),而对于非均质介质中纳米颗粒的迁移机制研究较少 (Bradford et al., 2009;Leij et al., 2013).Wu等 (2013)研究表明,饱和非均质介质中粗砂部分作为优势通道并形成优势流,说明介质的非均质性是影响水流状态的重要因素.Bradford等 (2004)模拟了纳米颗粒在双重渗透率模型中的运移,发现渗流速度影响纳米颗粒滞留曲线的形状,流速较大时更多纳米颗粒避开低渗透区域,使得模型边界处纳米滞留量减小.由于实际地下水含水系统构成复杂,非均质介质普遍存在,因此研究纳米颗粒在非均质多孔介质中的运移,并进行数值模拟预测,对于推动纳米颗粒环境行为的认识十分必要.
TOUGH2是目前国际上多孔及裂隙介质中多维、多相、多组分混合流体及热量运移的通用数值模拟程序之一,在地热储藏工程、核废料处置、环境评价和修复以及变饱和带水流和运移等领域均有广泛应用 (Pruess et al., 1999).TOUGH2采用模块化结构 (施小清等,2009),根据不同研究问题选择合适的EOS模块,将特定流体混合物的属性加入到控制方程中进行计算.EOS9nT模块最早用于胶体模拟,Moridis等 (2003)利用TOUGH2/EOS9nT有效模拟了对流、扩散、水动力弥散及动态胶体过滤等复杂作用下放射性胶体在非饱和带的迁移和阻滞过程.但目前鲜有TOUGH2在纳米颗粒运移方面的应用研究.
本文利用TOUGH2软件中EOS9nT模块,采用描述胶体运移的线性平衡及非平衡方程研究纳米颗粒在非均质多孔介质中的运移,并基于TOUGH2软件中独有的多重相互作用连续体 (MINC) 概念,在室内实验的基础上,模拟Nano-GO在非均质介质中的传输过程,探讨MINC方法刻画非均质多孔介质的可行性.
2 材料与方法 (Materials and methods) 2.1 纳米颗粒在饱和双区砂柱中的运移实验 2.1.1 实验材料实验中使用的GO购自ACS Material (Medford,MA).GO纳米颗粒呈片层结构,使用原子力显微镜可测得GO平均表面积平方根为 (582±111.2) nm,厚度为 (0.92±0.13) nm (Wu et al., 2013).实验开始前,将2.5 mg的KNO3加入到100 mL去离子水中,制备成25 mg·L-1的示踪剂溶液.同样,将2.5 mg的GO加入到100 mL去离子水中,使用NaCl调至对应离子强度 (1 mmol·L-1或20 mmol·L-1),将混合物超声2 h,制备成25 mg·L-1的Nano-GO稳定胶体悬液 (Wu et al., 2013),并将悬液pH调至5.6待用.实验中,使用粒度分析仪 (布鲁克海文仪器公司,美国) 测得悬液中GO颗粒在1 mmol·L-1离子强度下平均水力直径为 (474.2 ± 20.0) nm,在20 mmol·L-1离子强度下平均水力直径为 (577.4 ± 24.0) nm.用0.70 ~0.85 mm的粗石英砂和0.45~0.5 mm的细石英砂作为填装非均质砂柱的多孔介质,实验前需用稀硝酸 (2.5 mol·L-1) 和去离子水依次将石英砂洗净,并将其在40 ℃条件下烘干待用.
2.1.2 砂柱实验选取垂直放置的,内径2.5 cm,长度20 cm的聚丙烯柱作为实验砂柱装置,其进水及出水端分别铺设80目不锈钢纱网,以达到均匀水流的目的.装砂前,首先在砂柱纵截面处中设置一聚丙烯薄片 (长度25 cm,直径2.5 mm,厚度 < 1 mm),将砂柱分为左右两个区域,然后采用湿法,分别将粗砂、细砂装填于聚丙烯柱两区域中.装砂完成后,将聚丙烯薄片缓慢抽出,以此得到两侧渗透能力不同的非均质饱和砂柱 (图 1).砂柱进水端连接蠕动泵 (BT100-1F, Longer Pump),控制实验水流为2 mL·min-1的上升流.用去离子水或不含Nano-GO的背景溶液分别冲洗砂柱2 h,随后注入2个孔隙体积 (Pore Volume, PV) 示踪剂溶液或Nano-GO悬浮液,待注入结束后,随即用纯水或不含Nano-GO的背景溶液冲洗石英砂柱约6 PV.Nano-GO运移实验前,首先进行KNO3溶液的示踪实验,实验步骤与Nano-GO运移实验相同.实验中,根据两种介质装填的质量比,可等效换算得到粗砂与细砂在砂柱中所占体积比分别为0.53及0.47,进而得到其所占孔隙体积分别20.3 mL及18.0 mL.通过分别装填对应粗砂及细砂的均质砂柱,获得两种介质均质条件下的平均孔隙度数据,将其分别概化为本研究中非均质砂柱粗砂及细砂区域的平均孔隙度,数值分别为0.40及0.38.
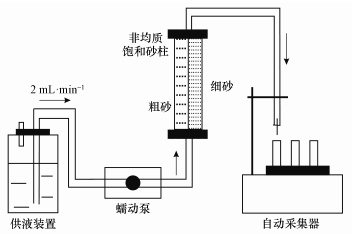 |
| 图 1 实验装置示意图 Fig. 1 Diagram of experimental installation |
在示踪剂溶液或Nano-GO悬浮液注入同时,采用自动部分收集器在砂柱出口端收集流出液 (BS-100A, 普阳科学仪器研究所, 南京),样品收集间隔为2 min.用紫外分光光度计 (尤尼柯仪器有限公司, 上海) 在220 nm (Feriancikova et al., 2012) 及230 nm (Liu et al., 2013) 波长分别测定流出液中KNO3及Nano-GO的吸光度.采用标准化相对浓度值,即测样浓度与初始浓度的比值 (C/C0) 来刻画流出端样品浓度的变化.所有实验均设2个平行实验,最终结果为2次实验结果的平均值.
2.2 基于TOUGH2/EOS9nT的数学模型 2.2.1 基于MINC概念的双重介质多重相互作用连续体 (Multiple Interacting Continua,MINC) 是TOUGH2软件处理裂隙介质模型的一种方法,最早由Pruess提出 (Pruess,1985),Xu等 (2001)介绍了MINC方法在化学反应溶质运移中的拓展应用.MINC的原理基于裂隙系统中流体压力、温度和化学浓度变化的传播瞬时发生,而在入渗到弱透水的基质时则较为缓慢 (许天福等,2012).裂隙和基质间局部基质状态 (即流体或溶质的扩散量) 的改变由其到裂隙壁的距离决定.因此,利用MINC方法设定适当的、相互嵌套的子网格,合理定义裂隙与基质间的水流联系,可以模拟裂隙与基质交界面处的驱动压力、温度以及浓度的梯度,解决裂隙岩体中水体流动和溶质扩散的问题,反映裂隙和基质间局部流体的相互反应交换作用.当仅指定二重连续体,MINC模型则简化为传统的双重孔隙模型或双重渗透模型 (图 2),本文采用的即双重渗透模型 (图 2c).双重渗透模型将基质之间也视作连续体,因此,全局流动不仅发生在裂隙网络之间,同时也发生在基质内部,一旦含水层条件受到扰动,两种渗透介质中均发生响应.而在裂隙与基质之间,水流则是局部的缓慢入渗过程.
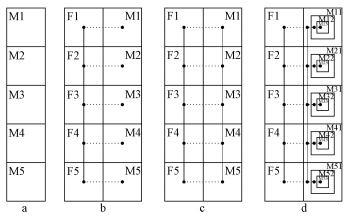 |
| 图 2 多孔介质概念模型 (Pruess et al., 1999)(a.等效连续介质模型,b.双重孔隙模型,c.双重渗透模型,d.多重连续介质模型) Fig. 2 Conceptual model of porous media (a.equivalent continuum model, b.dual-porosity model, c. dual-permeability model, d. multiple interacting continua model) |
EOS9nT模块假设模拟过程中水流为等温、无相变,忽略较低浓度的示踪物对液体密度和粘度的影响,由描述饱和或非饱和带地下水流运动机制的Richard方程 (式1) 和一组描述溶质 (或胶体) 运移的线性独立方程 (式2) 基于质量守恒进行计算模拟 (Moridis et al., 1999;Seol,2006):
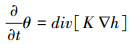
|
(1) |
式中,θ为饱和度 (m3·m-3);K为相对渗透系数 (m·s-1);h为水头 (m).
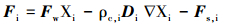
|
(2) |
式中,Fi为示踪物i的质量通量 (kg·m-1·s-1);Fw为水流通量 (kg·m-1·s-1);Fs, i为表面扩散作用引起的示踪物i变化量 (kg·m-1·s-1);Di为示踪物i的弥散张量 (m2·s-1);Xi为示踪物i在水溶液中的质量分数;ρc, i为胶体颗粒密度 (kg·m-3).
该模块能有效模拟示踪物 (或胶体) 的吸附、放射性衰变、对流、水动力弥散、分子扩散、胶体过滤、一级化学反应以及胶体协助下示踪物运移等过程.
示踪物 (或胶体) 在多孔介质中的存在形态主要包括水溶液中的自由态、吸附于多孔介质表面、参与化学反应以及受胶体协助运移等.胶体颗粒在通过多孔介质时受到胶体过滤作用的影响 (Yao et al., 1971),通过物理截留、沉淀和扩散作用迁移到固相介质颗粒表面.EOS9nT中,示踪物 (或胶体) 在孔隙或裂隙介质中的累积项可表示为:

|
(3) |
式中,ML, i, MAg, i, MR, i, MAc, i, MF, i分别为示踪物在水溶液、吸附于介质、参与化学反应、吸附于胶体颗粒及胶体过滤的质量 (kg·m-3).
其中,过滤胶体的质量表示为 (Moridis et al., 1999):
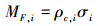
|
(4) |
式中,σi为单位多孔介质体积中胶体浓度 (m3·m-3).
当胶体沉淀速率远大于地下水流速,胶体过滤过程可用线性平衡方程来描述 (James et al., 1999):
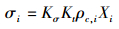
|
(5) |
式中,Kσ为分配系数 (m3·kg-1);Kt为一个无量纲的质量传递系数.
然而,实际情况下胶体过滤通常是非线性,理论预测结果常与实验观察结果有所偏差.因此,采用线性动态过滤模型 (Corapcioglu et al., 1987) 描述这一过程更为准确:

|
(6) |
式中,κ为动态过滤系数 (s-1),κ+为胶体向介质表面的吸附速率 (m3·kg-1·s-1)、κ-为胶体向介质表面的脱附速率 (s-1).κ+表示为 (Moridis et al., 1999):
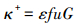
|
(7) |
式中,ε为多孔介质的过滤系数 (m-1);f为速度修正;u为达西流速 (m·s-1);G表示胶体过滤过程中关于胶体浓度σ的动态阻塞函数.κ-可以取零,也可以是κ+的函数.
3 模拟结果与讨论 (Results and discussion) 3.1 数值模型剖分及参数数值模型采用规则的长方体剖分方式构造一维柱状主网格,X方向与Y方向网格间距均为2.2 cm (保证其正方形横截面积与实验砂柱圆形截面积相等);Z方向共剖分42层,顶底边界层厚度为10-6 m,其余40层厚度均为0.5 cm.在此基础上利用MINC方法进行次级剖分,设置一组间距2.2 cm的平行裂隙,其中裂隙与基质部分体积各占50%,并假设基质-基质间存在全局水流,即双重渗透模型.将该模型与砂柱实验结合,粗砂区概化为裂隙介质区域,细砂区概化为基质区域.对于GO运移实验来说,采用上升流和下降流对实验结果没有影响 (Cai et al., 2015),此处模型顶部为定流量边界,底部为定水头边界,即模拟下降流.模拟时间与室内实验相同,首先稳定输入KNO3溶液 (或Nano-GO悬浮液)2400 s (约2 PV),随后背景溶液稳定输入7200 s.
模型主要水文地质参数如表 1所示.其中,孔隙度、裂隙所占体积分数由室内实验测得;石英砂密度取经验值;假设多孔介质渗透率为各向同性,利用EOS9nT模块,通过求解控制方程并结合概念模型的初始及边界条件,拟合实验穿透曲线,确定双区渗透率取值,得到裂隙与基质渗透率比值为2.5.其余模型计算相关参数与文献中 (Seol,2007) 的算例一致.
| 表 1 模型主要水文地质参数 Table 1 Main hydrogeological parameters of the model |
示踪物运移参数主要包括分子扩散系数、弥散度以及胶体过滤作用的分配系数或过滤系数等 (表 2).忽略介质表面对溶质的吸附作用,KNO3分子扩散系数参考文献 (Domenico et al., 2013);根据不同离子强度条件下Nano-GO的平均水力直径,通过Stokes-Einstein方程 (Bird et al., 1960) 可分别计算得到其分子扩散系数;弥散度利用EOS9nT模块拟合示踪剂KNO3穿透曲线获取.离子强度1 mmol·L-1条件下Nano-GO在多孔介质中受到线性平衡过滤作用,通过模型计算拟合实验数据得到分配系数分别为裂隙区2.00×10-6 m3·kg、基质区2.00×10-5 m3·kg;20 mmol·L-1条件下,线性平衡过滤作用对实验结果不能较好拟合,故采用更为准确的线性动态过滤模型 (Seol,2007),利用EOS9nT模块计算得到裂隙区过滤系数0.80 m-1、基质区20.00 m-1.
| 表 2 示踪剂运移主要参数 Table 2 Main parameters of tracer transportation |
根据模型边界条件,控制体系进流量与出流量均为2 mL·min-1,系统实际流速约为0.413 cm·min-1.由于两区域具有不同的渗透能力,裂隙区域实际流速0.739 cm·min-1,基质区域实际流速0.311 cm·min-1,双区实际流速比为2.375:1,渗透流速比2.5:1.
示踪剂KNO3穿透曲线 (图 3a) 的模拟结果与实验观测结果基本吻合,表现为明显的双峰和拖尾特征,为MINC方法刻画双重非均质介质的可行性提供了有力支持.由于运移过程中不考虑对示踪剂KNO3的吸附和沉淀反应作用,出流液最大相对浓度可达0.99.对比示踪剂KNO3在裂隙和基质两区域各自的穿透曲线和整体模拟曲线,不难发现模拟曲线为裂隙区和基质区各自穿透曲线叠加的结果.受裂隙区优先流影响,0.5 PV时流经裂隙区的KNO3已经运移到该区底部,出流液相对浓度值迅速增大到0.99,大约在1.0 PV时形成曲线平台;此时,通过基质区的KNO3也从底部边界流出.这表明,在0.5~1.0 PV,出流液中的KNO3主要经裂隙区传输,故模拟曲线到达第一个峰值的时间与裂隙区穿透曲线平台的形成大约在同一时期.1.0~2.3 PV时,通过基质区的KNO3出流浓度迅速增加,即模拟曲线中由基质区提供的示踪剂浓度所占比例增大,曲线再次攀升,到达第2个峰值.大约2.7 PV之后,随裂隙区出流液中KNO3的大量减少,模拟曲线迅速下降.约3.2~3.5 PV时,裂隙区出流液相对浓度已经趋于零,而基质区由于渗透能力较弱,出流液相对浓度仍保持在穿透曲线的平台阶段,系统出流浓度由基质区维持,出现第1次拖尾.此后,随基质区出流液相对浓度迅速下降,模拟曲线表现出第2次拖尾.
 |
| 图 3 KNO3和Nano-GO穿透曲线 Fig. 3 The break through curves of KNO3 and Nano-GO |
IS=1 mmol·L-1时,实验结果显示,Nano-GO的穿透曲线大体趋势与示踪剂KNO3相同 (图 3b),但由于纳米颗粒受到多孔介质的吸附及过滤作用,出流液所达到的最大相对浓度略有降低,约为0.97.考虑平衡过滤作用影响时,曲线在峰值和平台的拐点处与实验结果拟合更好,表明低离子强度下利用EOS9nT模块结合MINC方法模拟双重非均质介质中纳米颗粒的传输是可靠的.纳米颗粒受多孔介质表面对其吸附作用滞留在体系中,使得基质区峰值出现的时间推迟约0.3 PV.
IS=20 mmol·L-1时,由于纳米颗粒双电层被压缩,与石英砂表面之间的斥力减小,GO颗粒与石英砂表面之间的能量势垒曲线出现第2极小势能,并于该处沉积在石英砂表面 (Feriancikova et al., 2012;Sun et al., 2015),从而滞留在系统中,实验结果表明出流液相对浓度从0.97下降到不足0.60.随离子强度增大,传统的胶体平衡过滤模型无法拟合实验结果,采取了动态过滤模型.尽管Nano-GO模拟曲线与观测值在纳米颗粒悬浮液注入阶段误差较大,但总体上升趋势基本一致,背景溶液注入阶段拟合良好 (图 3c).Nano-GO穿透曲线仅表现为一个缓慢上升的峰和明显拖尾,并未出现平台;双区峰值均有下降,基质区峰值降低显著,且峰值出现时间稍有推迟.同时,模拟结果还显示,在渗透能力较弱的基质区Nano-GO滞留量远大于裂隙区.这与Sun等 (2015)的研究结果一致,即GO穿透曲线呈现非对称且倾斜向上的形状.这是由于随时间增加,石英砂表面的沉积位点逐渐被GO颗粒所占据,沉积位点数量不断减少,使得砂柱流出端GO穿透浓度持续增大.
由于在20 mmol·L-1离子强度条件下GO颗粒在石英砂表面的沉积量随时间降低,因此其沉积过程无法简单地用连续一阶动力学方程进行描述.目前,已有研究采用二阶动力学方程来描述GO颗粒的此种沉积及运移状态 (Bradford et al., 2006;Bradford et al., 2009).因此,后续需针对EOS9nT一阶动力学模型描述GO运移存在的局限性进行修正,从而更精确的模拟较大离子强度下纳米颗粒的运移行为.
3.3 渗透率对纳米颗粒在非均质介质中传输运移的敏感性影响渗透率是表征岩体自身对不同流体的固有渗透性能,与渗流液体的性质无关.IS=1 mmol·L-1时,在模型中分别设置不同裂隙与基质渗透率比来调整各自区域的渗流速度,探讨其对纳米颗粒在双重介质中运移的影响.
模拟得到Nano-GO穿透曲线 (图 4),曲线到达峰值的时间以及峰值对应的相对浓度大小均与渗流速度有关.表 3分别列出了3种渗透率比值时,双区的渗流速度:随渗透率比值增大,裂隙区渗流速度逐渐增大,在穿透曲线上表现为到达第1个峰值平台的时间提前 (从1.5 PV提前到1.0 PV);而基质区则相反,渗流速度减小,造成穿透曲线第2个峰形延迟.
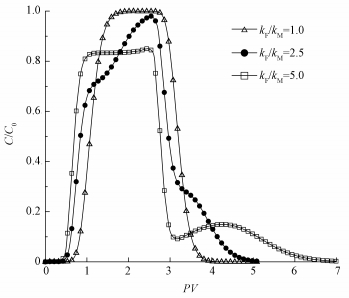 |
| 图 4 不同渗透率比Nano-GO穿透曲线 Fig. 4 The break through curve of Nano-GO with different permeability ratio |
| 表 3 不同渗透率比值时双区渗流速度 Table 3 Permeable velocity of dual-permeability media with different permeability ratio |
双区流速比不同时,裂隙区和基质区各自曲线叠加的结果也不同:流速比值接近1.0时,系统穿透曲线表现出较好的对称性,裂隙区与基质区各自穿透曲线峰值出现的时间相近,可视为两条曲线同时在峰值处叠加,流经两个区域的纳米颗粒对系统穿透曲线的相对浓度贡献均等,出流液最大相对浓度达0.95以上.随流速比增大,裂隙区与基质区的穿透曲线到达各自峰值的时间差异越大,表现为裂隙区到达峰值的时间提前,而基质区到达峰值的时间延后,造成两个峰形相隔越远,系统穿透曲线的最大相对浓度由裂隙区传输的纳米颗粒占主导,对应出流液所能达到的最大相对浓度值减小,如图 4中,双区渗透率比值为5.0时,系统穿透曲线最大相对浓度仅为0.84.
3.4 三重介质和双重介质的对比探讨非均质多孔介质概化是模型模拟的难点之一,前文为MINC方法模拟多重介质提供了一定依据.此处建立具有一组平行裂隙的三重非均质介质,裂隙区域体积分数为0.5,基质区域剖分为两重,体积分数各占0.25,三重区域的渗透率比为12:3:1,其他参数与前文一致.假设模型中同时存在裂隙-裂隙、基质-基质间的全局流动,即三重渗透模型,每重区域具有相同的质量交换面积,垂向通量仅与介质渗透性有关.此处考虑溶质KNO3在三重非均质介质中的运移传输,忽略介质的吸附作用.
总穿透曲线的形状受三重区域各自峰值叠加时刻的影响 (图 5).在0.9~1.7 PV和3.0~3.7 PV阶段,均为某一区域峰值平台段与另一区域浓度突变段叠加,总穿透曲线表现为斜率减小;当两个峰值平台叠加时,总穿透曲线上也表现出稳定的峰值平台,如1.7~2.5 PV阶段.3.0 PV之后,第二重基质区域峰值段与其他两个区域拖尾段叠加,总穿透曲线出现一个低峰,拖尾现象不明显.由于该时刻第二重基质区域的流量通量仅占总流量的1/16,而其他两区出流浓度基本为零,故总出流浓度被稀释,总穿透曲线最大相对浓度约0.056.
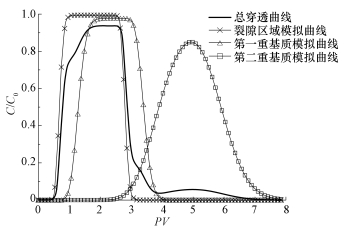 |
| 图 5 三重介质KNO3穿透曲线 Fig. 5 The break through curve of KNO3in triple-permeability model media |
结合三重区域各自的渗流速度 (表 4) 和三重介质不同渗透率比时KNO3穿透曲线 (图 6),发现较之渗透率比为12:3:1,当三重区域渗透率比为10:2:1,第一重基质渗流速度减小,而裂隙和第二重基质渗流速度则有所增大.这使两重基质区域各自的穿透曲线相互靠近,第一重基质区域曲线的拖尾与第二重机质区域曲线的峰值平台在4.0~4.5 PV处叠加,该处曲线上观察不到明显的低峰.
| 表 4 不同渗透率比时三重区域渗流速度 Table 4 Permeable velocity of triple-porosity media with different permeability ratio |
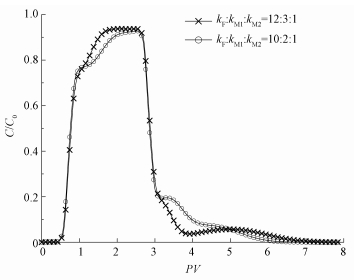 |
| 图 6 三重介质不同渗透率比KNO3穿透曲线 Fig. 6 The break through curve of KNO3 in triple-permeability model media with different permeability ratio |
1) MINC方法能够有效模拟双重介质,非均质性是决定优先流及Nano-GO运移行为的主要物理因素.基于EOS9nT模块中的线性平衡过滤模型可有效模拟低离子强度下双重非均质介质中纳米颗粒运移,在穿透曲线上表现出双峰和拖尾特征,可视为裂隙区和基质区各自穿透曲线叠加的综合效果,表明了MINC方法模拟非均质介质是可行的.但即使采用动态过滤模型仍无法精确模拟高离子强度下纳米颗粒的运移,说明EOS9nT模块采用的一阶动力学模型仍有一定局限性.实验结果表明,Nano-GO在饱和非均质多孔介质中的运移受离子强度的影响,相同背景溶液条件下,随着离子强度增大,纳米颗粒在饱和非均质介质中的迁移能力减弱.
2) 通过双渗模型中渗透率的敏感性分析发现:随着非均质性增强,也即双重区域渗透率的比值越大,裂隙区优先流渗流速度越快,穿透曲线越早到达峰值;而对应基质区渗流速度则越缓慢,出现峰值的时间延迟,造成两个峰形间隔越远,系统曲线双峰现象更明显.
3) 通过三重介质和双重介质的对比分析,发现受优先流影响,总穿透曲线的形状与三重区域各自曲线叠加时刻有关,表现出峰值/拖尾的增强或削弱.在合适的渗透率比值下,可能出现3个峰值和拖尾.
| [${referVo.labelOrder}] | Bird R B, Stewart W E, Lightfoot E N. 1960. Transport phenomena[M]. New York: John Wiley & Sons: 514. |
| [${referVo.labelOrder}] | Bradford S A, Bettahar M. 2006. Concentration dependent transport of colloids in saturated porous media[J]. Journal of Contaminant Hydrology, 82(1) : 99–117. |
| [${referVo.labelOrder}] | Bradford S A, Bettahar M, Simunek J, et al. 2004. Straining and attachment of colloids in physically heterogeneous porous media[J]. Vadose Zone Journal, 3(2) : 384–394. DOI:10.2136/vzj2004.0384 |
| [${referVo.labelOrder}] | Bradford S A, Kim H N, Haznedaroglu B Z, et al. 2009. Coupled factors influencing concentration-dependent colloid transport and retention in saturated porous media[J]. Environmental Science & Technology, 43(18) : 6996–7002. |
| [${referVo.labelOrder}] | Bradford S A, Torkzaban S, Leij F, et al. 2009. Modeling the coupled effects of pore space geometry and velocity on colloid transport and retention[J]. Water Resources Research, 45(2) : 1–15. |
| [${referVo.labelOrder}] | Bradford S A, Yates S R, Bettahar M, et al. 2002. Physical factors affecting the transport and fate of colloids in saturated porous media[J]. Water Resources Research, 38(12) : 63–1. |
| [${referVo.labelOrder}] | Cai L, Zhu J, Hou Y, et al. 2015. Influence of gravity on transport and retention of representative engineered nanoparticles in quartz sand[J]. Journal of Contaminant Hydrology, 181 : 153–160. DOI:10.1016/j.jconhyd.2015.02.005 |
| [${referVo.labelOrder}] | Chowdhury I, Duch M C, Mansukhani N D, et al. 2013. Colloidal properties and stability of graphene oxide nanomaterials in the aquatic environment[J]. Environmental Science & Technology, 47(12) : 6288–6296. |
| [${referVo.labelOrder}] | Corapcioglu M Y, Abboud N M, Haridas A.1987.Governing equations for particle transport in porous mediaAdvances in transport phenomena in porous media[M].Springer.269-342 |
| [${referVo.labelOrder}] | Domenico P A, Schwartz F W. 2013. 物理与化学水文地质学 (第2版)[M]. 王焰新等译. 北京: 高等教育出版社. 285 |
| [${referVo.labelOrder}] | Dunphy Guzman K A, Taylor M R, Banfield J F. 2006. Environmental risks of nanotechnology: National nanotechnology initiative funding, 2000-2004[J]. Environmental Science & Technology, 40(5) : 1401–1407. |
| [${referVo.labelOrder}] | Fang J, Xu M J, Wang D J, et al. 2013. Modeling the transport of TiO2 nanoparticle aggregates in saturated and unsaturated granular media: effects of ionic strength and pH[J]. Water Research, 47(3) : 1399–1408. DOI:10.1016/j.watres.2012.12.005 |
| [${referVo.labelOrder}] | Feriancikova L, Xu S. 2012. Deposition and remobilization of graphene oxide within saturated sand packs[J]. Journal of Hazardous Materials, 235 : 194–200. |
| [${referVo.labelOrder}] | Godinez I G, Darnault C J G. 2011. Aggregation and transport of nano-TiO2 in saturated porous media: effects of pH, surfactants and flow velocity[J]. Water Research, 45(2) : 839–851. DOI:10.1016/j.watres.2010.09.013 |
| [${referVo.labelOrder}] | Hendren C O, Mesnard X, Dro ge J, et al. 2011. Estimating production data for five engineered nanomaterials as a basis for exposure assessment[J]. Environmental Science & Technology, 45(7) : 2562–2569. |
| [${referVo.labelOrder}] | James S C, Chrysikopoulos C V. 1999. Transport of polydisperse colloid suspensions in a single fracture[J]. Water Resources Research, 35(3) : 707–718. DOI:10.1029/1998WR900059 |
| [${referVo.labelOrder}] | Johnson P R, Sun N, Elimelech M. 1996. Colloid transport in geochemically heterogeneous porous media: Modeling and measurements[J]. Environmental Science & Technology, 30(11) : 3284–3293. |
| [${referVo.labelOrder}] | Klaine S J, Alvarez P J, Batley G E, et al. 2008. Nanomaterials in the environment: behavior, fate, bioavailability, and effects[J]. Environmental Toxicology and Chemistry, 27(9) : 1825–1851. DOI:10.1897/08-090.1 |
| [${referVo.labelOrder}] | Lanphere J D, Luth C J, Walker S L. 2013. Effects of solution chemistry on the transport of graphene oxide in saturated porous media[J]. Environmental Science & Technology, 47(9) : 4255–4261. |
| [${referVo.labelOrder}] | Lecoanet H F, Bottero J Y, Wiesner M R. 2004. Laboratory assessment of the mobility of nanomaterials in porous media[J]. Environmental Science & Technology, 38(19) : 5164–5169. |
| [${referVo.labelOrder}] | Leij F J, Bradford S A. 2013. Colloid transport in dual-permeability media[J]. Journal of contaminant hydrology, 150 : 65–76. DOI:10.1016/j.jconhyd.2013.03.010 |
| [${referVo.labelOrder}] | Lenhart J J, Saiers J E. 2002. Transport of silica colloids through unsaturated porous media: Experimental results and model comparisons[J]. Environmental Science & Technology, 36(4) : 769–777. |
| [${referVo.labelOrder}] | Liu L, Gao B, Wu L, et al. 2013. Deposition and transport of graphene oxide in saturated and unsaturated porous media[J]. Chemical Engineering Journal, 229 : 444–449. DOI:10.1016/j.cej.2013.06.030 |
| [${referVo.labelOrder}] | Mauter M S, Elimelech M. 2008. Environmental applications of carbon-based nanomaterials[J]. Environmental Science & Technology, 42(16) : 5843–5859. |
| [${referVo.labelOrder}] | Moridis G J, Hu Q, Wu Y S, et al. 2003. Preliminary 3-D site-scale studies of radioactive colloid transport in the unsaturated zone at Yucca Mountain, Nevada[J]. Journal of Contaminant Hydrology, 60(3) : 251–286. |
| [${referVo.labelOrder}] | Moridis G J, Wu Y S, Pruess K.1999.EOS9nT: A TOUGH2 module for the simulation of water flow and solute/colloid transport in the subsurface[R].LBNL-42351.California: Lawrence Berkeley National Lab.10-13 |
| [${referVo.labelOrder}] | Pruess K, Naras; mhan T N. 1985. A practical method for modeling fluid and heat flow in fractured porous media[J]. Society of Petroleum Engineers Journal, 25(1) : 14–26. DOI:10.2118/10509-PA |
| [${referVo.labelOrder}] | Pruess K, Oldenburg C, Moridis G.1999.TOUGH2 User's Guide Version 2[R].LBNL-43134.California:Lawrence Berkeley National Laboratory.1, 152-154 |
| [${referVo.labelOrder}] | Seol Y.2006.Design Document for TOUGH2 V1.11MEOS9NT V2.0[R].10065-DD-1.11MEOS9NTV2.0-01.California: Lawrence Berkeley National Lab.14-15 |
| [${referVo.labelOrder}] | Seol Y.2007.User Information Document for TOUGH2 V1.11MEOS9NT V2.0[R].10065-VID-1.11MEOS9NTV2.0-01. California:Lawrence Berkeley National Lab.34-35(US) |
| [${referVo.labelOrder}] | 施小清, 张可霓, 吴吉春. 2009. TOUGH2软件的发展及应用[J]. 工程勘察, 2009, 37(10) : 29–34. |
| [${referVo.labelOrder}] | 孙慧敏, 殷宪强, 曹秀蓉. 2012a. 离子强度对蒙脱石胶体在饱和多孔介质中运移与释放的影响[J]. 环境科学学报, 2012a, 32(5) : 1120–1125. |
| [${referVo.labelOrder}] | 孙慧敏, 殷宪强, 王益权. 2012b. pH对粘土矿物胶体在饱和多孔介质中运移的影响[J]. 环境科学学报, 2012b, 32(2) : 419–424. |
| [${referVo.labelOrder}] | Sun Y, Gao B, Bradford S A, et al. 2015. Transport, retention, and size perturbation of graphene oxide in saturated porous media: Effects of input concentration and grain size[J]. Water Research, 68 : 24–33. DOI:10.1016/j.watres.2014.09.025 |
| [${referVo.labelOrder}] | Tian Y, Gao B, Silvera-Batista C, et al. 2010. Transport of engineered nanoparticles in saturated porous media[J]. Journal of Nanoparticle Research, 12(7) : 2371–2380. DOI:10.1007/s11051-010-9912-7 |
| [${referVo.labelOrder}] | Tosco T, Bosch J, Meckenstock R U, et al. 2012. Transport of ferrihydrite nanoparticles in saturated porous media: role of ionic strength and flow rate[J]. Environmental Science & Technology, 46(7) : 4008–4015. |
| [${referVo.labelOrder}] | Tufenkji N, Elimelech M. 2005. Breakdown of colloid filtration theory: Role of the secondary energy minimum and surface charge heterogeneities[J]. Langmuir, 21(3) : 841–852. DOI:10.1021/la048102g |
| [${referVo.labelOrder}] | Wang C, Bobba A D, Attinti R, et al. 2012. Retention and transport of silica nanoparticles in saturated porous media: effect of concentration and particle size[J]. Environmental Science & Technology, 46(13) : 7151–7158. |
| [${referVo.labelOrder}] | Wu L, Liu L, Gao B, et al. 2013. Aggregation kinetics of graphene oxides in aqueous solutions: experiments, mechanisms, and modeling[J]. Langmuir, 29(49) : 15174–15181. DOI:10.1021/la404134x |
| [${referVo.labelOrder}] | 许天福, 金光荣, 岳高凡, 等. 2012. 地下多组分反应溶质运移数值模拟:地质资源和环境研究的新方法[J]. 吉林大学学报:地球科学版, 2012, 42(5) : 1410–1425. |
| [${referVo.labelOrder}] | Xu T, Pruess K. 2001. Modeling multiphase non-isothermal fluid flow and reactive geochemical transport in variably saturated fractured rocks: 1[J]. Methodology[J].American Journal of Science, 301(1) : 16–33. DOI:10.2475/ajs.301.1.16 |
| [${referVo.labelOrder}] | Yao K M, Habibian M T, O'Melia C R. 1971. Water and waste water filtration[J]. Concepts and applications[J].Environmental Science & Technology, 5(11) : 1105–1112. |
 2017, Vol. 37
2017, Vol. 37


