近年来, 空气污染日渐成为一个严峻的问题.空气质量恶化对人身健康和环境存在巨大的或者潜在的危害 (Dimitriou et al., 2013;Pope et al., 2002;Li et al., 2009).因此, 大气污染物浓度预报非常重要, 它不仅对人们的日常生活有所帮助, 而且对政府制定相关政策具有指导意义.
目前国内外空气质量模型主要采用机理模型和非机理模型.机理模型预报形式主要为数值预报, 数值预报模型涉及复杂的物理化学过程, 要求建立相对完备的排放源、气象及污染物扩散过程等物理化学过程的相关模型.非机理模型需要的数据量相对较少, 通过历史的数据, 捕捉数据特征, 得到污染物浓度变化规律.总的来讲, 以统计模型和神经网络模型为代表的非机理模型, 以给出相对准确的预报值为目标, 不过多追究结果产生的复杂机理过程, 模型相对简单, 便于实际应用.
在城市区域内, 交通运输和供热对大气PM10的贡献最为突出 (Unal et al., 2013).生物质燃烧也是有代表性的颗粒物排放源 (Nava et al., 2013).同时, 城市的污染物浓度也跟气象条件 (Bampadimos et al., 2013) 和城市布局有关系 (何健等, 2002).在城区内, 影响环境空气质量的因素更加复杂, 建立城市区域的空气质量预报模型难度更大.
综合考虑不确定性因素的非机理模型的量化预测方式在国内外有广泛的应用:多元线性回归预测污染物浓度 (黄思等, 2009;魏璐等, 2009;刘闽等, 2014), 基于时间序列的空气质量分析 (孟晓艳等, 2011;陈亚玲等, 2013; Diaz et al., 2008), 利用模式识别理论对大气污染物浓度进行预测 (熊德琪等, 1993), 基于灰色理论的大气污染物浓度预测模型 (常莉, 2002;代伟等, 2011), 支持向量机的大气污染物浓度预测模型 (Shaban et al., 2016;Moazami et al., 2016;秦喜文等, 2016), 利用BP神经网络模型对大气污染物浓度进行预测 (Grivas et al., 2006;Paschalidou et al., 2011;刘永红等, 2009;谢超等, 2015;杨云等, 2016).BP神经网络在大气污染物浓度预测方面有着广泛的应用, 且预测效果较好.BP神经网络的方法属于机器学习的方法, 学习速度快并且适应能力强.人工神经网络可以处理非线性的问题 (Huo et al., 2013;Comrie et al., 2013).
目前基于BP神经网络对大气污染物浓度预测的研究中, 主要利用一些方法筛选对污染物浓度影响较大的因素作为输入变量, 以提高预测精度.如主成分分析法 (Sousa et al., 2007;李嵩等, 2015)、Person相关系数法 (王国胜等, 2015;田静毅等, 2015)、层次聚类算法 (姚宁等, 2015), 结合气象条件进行筛选的气象相似性准则 (李璐等, 2013;Liu et al., 2015) 等.通过对输入变量进行筛选, BP神经网络的预测精度有所提高.Dombi等 (1995)提出了利用平均影响值 (MIV, Mean Impact Value) 的方法来反映神经网络中权重矩阵的变化情况, 基于BP神经网络的计算结果筛选变量的方法, 尚未有人在污染物浓度预测中使用该方法.
利用BP神经网络对某种污染物日均浓度进行预测, 大多考虑前一日该污染物日均浓度对次日的影响, 忽略了其他污染物前一日浓度对次日该污染物日均浓度的影响.本文的污染物浓度预测模型考虑到这种影响, 输入变量包含前一日SO2、NO2、O3、CO、PM10、PM2.5等6种污染物的日均浓度.
本文利用空气质量监测数据, 应用BP神经网络建立SO2、NO2、O3、CO、PM10、PM2.5这6种污染物日均浓度的预测模型.首先, 利用平均影响值 (MIV) 的方法对输入变量进行筛选, 将筛选出的变量作为神经网络的输入变量, 然后应用BP神经网络对各污染物浓度进行预测, 并与未经变量筛选的预测结果进行比较.
2 方法 (Methods)人工神经网络是模拟人脑神经元信号传输的模型.人工神经网络是一个网状结构, 各连接层是平行关系, 各层内包含基本的操作单元, 称为节点.如图 1所示网络结构, 包含3层, 输入层、隐含层和输出层.输入数据存储在输入层节点中, 数据通过隐含层传输至输出层.各层的节点与相邻层的每一个节点相连, 每层某个节点的输入数据是上一层的每个节点输出数据乘以权重后的加和.隐含层为转换层, 可以对数据进行非线性转换, 含有一个隐含层的神经网络可以表示任意的输入输出的映射关系.隐含层每个节点输入数据经过传递函数非线性转换得到节点的输出数据, 传递函数通常使用Sigmoid函数.BP神经网络是一种前馈神经网络, 采用反向传播算法, 即BP (Back-Propagation) 算法.
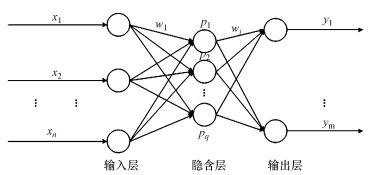 |
| 图 1 人工神经网络结构 Fig. 1 Architecture of one hidden layer feed-forward neural network |
BP算法的原理是将模拟输出值和期望输出值的误差平方和作为神经网络的误差, 将误差反向传播, 从输入层至输出层, 采用不同的算法调整网络权值和阈值, 本文采用附加动量的梯度下降法, 调整权值后信号再正向传播得到模拟输出值, 若误差不满足要求, 将误差再次反向传播, 继续调整权值, 使BP神经网络预测输出不断逼近期望输出, 直至误差满足要求 (王小川等, 2013).具体流程见图 2.
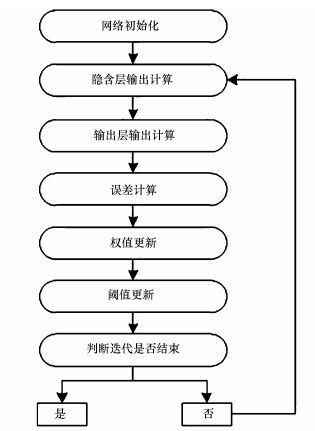 |
| 图 2 BP神经网络算法流程图 Fig. 2 Flowchart of Back Propagation (BP) neural network algorithm |
研究采用的数据为2014—2015年昆明市5个监测点的污染物浓度日均值, SO2、NO2、O3、PM10、PM2.5等5种污染物浓度单位为μg·m-3, CO浓度单位为mg·m-3.
3.2 数据的预处理 3.2.1 数据的归一化因为各污染物之间量纲不同, 且为了提高训练速度和灵敏性, 避免Sigmoid过饱和, 对污染物数据进行归一化处理, 使之范围控制在0~1之间 (柳小桐, 2010).但是有研究表明归一化后的数据在0.2~0.8之间 (郭庆春等, 2014), 可以使模型有一定的外推能力.本文选择第2种方法, 数据归一化算法为:
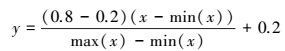
|
(1) |
式中, y为归一化后的数据, x为原始数据, max (x) 和min (x) 为原始数据中的最大值和最小值.
3.2.2 基于平均影响值的变量筛选MIV为确定输入神经元对输出神经元影响大小的一个指标, 符号代表相关方向, 绝对值代表影响的相对重要性.具体计算过程如下.
① 网络训练终止后, 训练样本x在其原值的基础上加/减10%, 构成两个新的训练样本Q1、Q2.
② Q1、Q2分别作为仿真用样本利用训练好的网络进行仿真, 得到两个仿真结果A1、A2.
③ E=A1-A2即为变动自变量后对输出结果产生的影响变化值, 将E按照样本的个数进行平均, 即为MIV.其变量筛选流程见图 3.
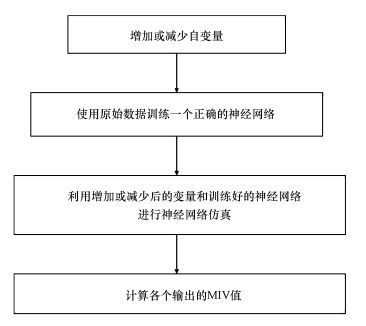 |
| 图 3 MIV方法的变量筛选流程图 Fig. 3 Flowchart of sample selection using MIV |
以昆明市关上监测点为例, 利用BP神经网络建立大气污染物浓度预测模型.有研究表明, 当天的污染物浓度与前5 d的浓度呈现出比较强的非线性关系 (姚宁等, 2015), 选取2014-01-01至2015-11-28 SO2、NO2、O3、CO、PM10、PM2.5等6种污染物的连续时间序列的浓度数据进行建模, 每1组数据包括输入数据和输出数据, 输入数据为某种污染物前5 d的浓度数据和前1 d的其他5种污染物浓度数据共10项, 输出数据为1种污染物浓度, 共694组数据.首次建立模型利用350组数据建立模型, 预测第351组数据, 随后每次预报训练数据增加一组最新实测数据, 预报下一组数据, 每次预报都重新调整权值, 实现动态预报.利用MIV方法筛选出对模型影响较大的变量, 筛选得到的变量作为输入变量进行BP神经网络预测.
4.1 BP神经网络构建BP神经网络模型主要需要确定以下参数:神经网络的层数, 输入层、输出层、隐含层的节点个数, 各层神经元传递函数, 训练方法.
4.1.1 神经网络规模确定本研究采用一个隐含层的BP神经网络, 即神经网络层数为3.对6种污染物预测分别建立模型, 输入变量为某种污染物前5 d的浓度数据和前1 d其他5种污染物, 即输入层、输出层节点个数均为10和1.隐含层节点的个数靠经验公式 (2) 确定 (韩立群, 2002).
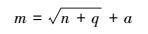
|
(2) |
式中, n为输入层节点个数, q为输出层节点个数, a为0~10的整数, m为隐含层节点个数, 则m的取值范围为3~14.经过试验, 确定SO2、NO2、O3、CO、PM10、PM2.5这6种污染物预测模型的隐含层节点个数分别为7、5、4、3、5、3.
4.1.2 神经网络的训练传递函数通常用Sigmoid函数, 经过试验, 确定隐含层的传递函数表达式见式 (3).权重学习方法为附加动量项的梯度下降法.
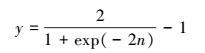
|
(3) |
利用4.1节建立的BP神经网络, 结合MIV方法, 筛选模型输入变量.神经网络每次训练的初始权重都不同, 则每次得到的MIV不同, 对每一种污染物浓度预测模型进行变量筛选时, 计算50次MIV, 带符号求和 (Li et al., 2013), 表 1~6为6个预测模型输入变量的MIV绝对值降序排列.SO2和O3预测模型选取排名前5的变量, NO2预测模型选取排名前7的变量, CO、PM10和PM2.5预测模型选取排名前6的变量.这些变量的MIV绝度值累积百分比不小于85%(Chen et al., 2013).
| 表 1 SO2预测模型输入变量MIV Table 1 MIV of input in SO2 forecast model |
| 表 2 NO2预测模型输入变量MIV Table 2 MIV of input in NO2 forecast model |
| 表 3 O3预测模型输入变量MIV Table 3 MIV of input in O3 forecast model |
| 表 4 CO预测模型输入变量MIV Table 4 MIV of input in CO forecast model |
| 表 5 PM10预测模型输入变量MIV Table 5 MIV of input in PM10 forecast model |
| 表 6 PM2.5预测模型输入变量MIV Table 6 MIV of input in PM2.5 forecast model |
将4.2节筛选出的变量作为输入变量, 由于输入变量个数发生变化, BP神经网络的输入层节点个数和隐含层节点个数也会相应发生变化, 经过试验, SO2、NO2、O3、CO、PM10、PM2.5这6种污染物预测模型的隐含层个数分别为7、3、4、6、5、4.BP神经网络模型建模时, 除输入层和隐含层节点个数不同, 其他参数同4.1节, 对6种污染物浓度进行预测.
5 结果 (Results) 5.1 关上监测点的结果分析基于BP神经网络, 分别将MIV方法筛选出的变量和未经筛选的变量作为输入变量, 对6种污染物浓度进行预测, 得到预测结果.利用预测值与实测值的平均数比值、标准偏差STD的比值、标准化平均偏差NMB、标准化平均误差NME、均方根误差RMSE、可决系数R2对预测结果进行评估 (表 7).平均数比值和标准偏差比值越接近1说明预测值和实测值的平均值和标准偏差越接近, NMB、NME、RMSE绝对值越小说明效果越好, R2越大且接近1, 表示相关性越高, 说明预测值越接近于实测值.为方便叙述, 未经变量筛选的方案为方案A, 即为4.1节建立的模型, 经过变量筛选的方案为方案B, 即为4.2节所建模型.各指标的表达式如下.
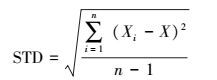
|
(4) |
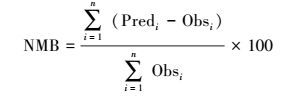
|
(5) |
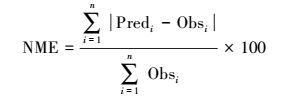
|
(6) |
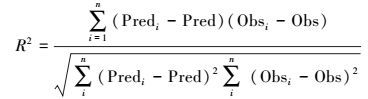
|
(8) |
| 表 7 两种方案评估指标对比 Table 7 Comparison between evaluation index of two methods |
式中, x为n个样本的平均值, Xi为样本值, Predi为第i个预测值, Obsi为第i个实测值, Pred为所有预测值的平均值, Obs为所有实测值的平均值.
方案A和方案B两种方案对污染物浓度的预测结果较好, 趋势与实测值一致, 且两种方法对污染物的浓度值预测结果与实测值吻合度较高.如图 4所示.用2种方法得到的预测值的平均值和标准偏差分别与实测值的平均值与标准偏差做比值计算, 可以看出2种方法的平均值均接近实测值的平均值.2种方法得到的预测值的标准偏差与实测值的标准偏差比值均大于0.6.两种方法的NMB均小于18, NME均小于34, RMSE均小于25, R2除方案A的PM10均大于0.6, 方案A中PM10的R2为0.57.
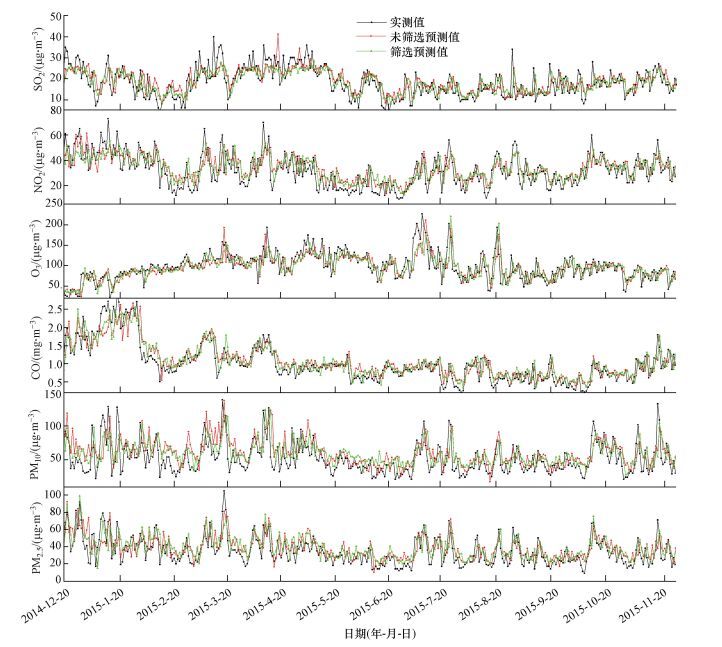 |
| 图 4 关上监测点各污染物浓度预测值与实测值对比 Fig. 4 Comparison between prediction and observation of pollutants in Guanshang |
SO2、PM2.5的各项指标显示, 方案B的模拟效果均比方案A的效果好.对于O3的RMSE和PM10的NME, 方案A预测效果比方案B预测效果好.NO2的各项指标中, 除了NME方案A和方案B相等, 其他指标方案A优于方案B, CO的各项指标中, NME方案B比方案A效果好, 其他指标方案A比方案B好.在实际预报中, SO2、O3、PM10、PM2.5的预报方法选择4.2节所建立的模型, NO2、CO预报方法选择4.1节建立的模型.
5.2 其他4个监测点的结果分析对昆明市区东风东路、金鼎山、碧鸡广场和龙泉镇等4个监测点也建立了污染物浓度预测模型, 建立模型的步骤同第4.1~4.3节, 结果如表 8所示.
| 表 8 两种方案评估指标对比 Table 8 Comparison between evaluation index of two methods |
4个监测点各项污染物浓度的预测平均值与实测平均值的比值多数控制在0.94~1.10之间, 标准偏差的比值大于0.6, 模拟结果较好, 标准化平均偏差均小于17, 标准化平均误差小于40, 均方根误差小于30, R2大多大于0.6, 少数几个位于0.3~0.6之间.
总的来说, 方案B的模拟效果优于方案A, 少数几个模型的方案B模拟效果比方案A差, 实际预报中选取模拟效果好的模型.
6 结论 (Conclusions)1) BP神经网络模型中, 将前1 d所有污染物浓度数据和前5 d某种污染物浓度数据作为预报的输入变量, 对某一种污染物浓度进行预报, 可以较好的对SO2、NO2、O3、CO、PM10、PM2.56种污染物浓度进行预报, 预测的浓度水平和变化趋势与实测值的变化吻合度较高.344组预测值的平均值与实测值的平均值的比值非常接近1, 标准偏差比值均大于0.6, NMB均小于17, NME均小于40, RMSE均小于30, R2多大于0.6.
2) 昆明市关上监测点的污染物浓度预报模型, 利用MIV方法对输入变量筛选, 有助于提高BP神经网络对SO2、O3、PM10、PM2.5的预报结果准确性.各项评估指标中, 除O3的均方根误差和PM10的标准化平均偏差, 其它经过变量筛选的神经网络预测指标均好于未经变量筛选的神经网络预测结果.变量筛选前的NO2和CO的预测结果比变量筛选后的预测效果好.
3) 模型使用神经网络方法可以相对准确的得到大气污染物浓度指标的预报结果, 与复杂且计算成本较高的机理模型相比较, 更适用于复杂不确定因素影响较强的预报环境, 能够为大气监测预报提供适应性强的预测方法.
| [${referVo.labelOrder}] | BarmPadimos I, Hueglin C, Keller J, et al. 2011. Influence of meteorology on PM10 trends and variability in Switzerland from 1991 to 2008[J]. Atmospheric Chemistry and Physics, 11(4) : 1813–1835. DOI:10.5194/acp-11-1813-2011 |
| [${referVo.labelOrder}] | Chen J H, Li H K, Sheng D R, et al. 2015. A hybrid data-driven modeling method on sensor condition monitoring and fault diagnosis for power plants[J]. Electrical Power and Energy Systems, 71 : 274–284. DOI:10.1016/j.ijepes.2015.03.012 |
| [${referVo.labelOrder}] | Comrie A C. 1997. Comparing neural networks and regression models for ozone forecasting[J]. Journal of the Air & Waste Management Association, 47(6) : 653–663. |
| [${referVo.labelOrder}] | 常莉. 2011. 灰色预测模型及应用[J]. 吉林化工学院学报, 2011, 19(4) : 93–94. |
| [${referVo.labelOrder}] | 陈亚玲, 赵志杰. 2013. 基于小波变换与传统时间序列模型的臭氧浓度多步预测[J]. 环境科学学报, 2013, 33(2) : 339–345. |
| [${referVo.labelOrder}] | 代伟, 李克国, 曲东. 2011. 等维灰数递补动态模型在秦皇岛市大气污染预测中的应用[J]. 安徽农业科学, 2011, 39(18) : 11026–11027. DOI:10.3969/j.issn.0517-6611.2011.18.112 |
| [${referVo.labelOrder}] | Diaz Robles L A, Ortega J C, Fu J S, et al. 2008. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas:The case of Temuco, Chile[J]. Atmospheric Environment, 42(35) : 8331–8340. DOI:10.1016/j.atmosenv.2008.07.020 |
| [${referVo.labelOrder}] | Dimitriou K, Kassomenos P A, Paschalidou A K. 2013. Assessing air quality with regards to its effect on human health in the European Union through air quality indices[J]. Ecological Indicators, 27 : 108–115. DOI:10.1016/j.ecolind.2012.11.023 |
| [${referVo.labelOrder}] | Dombi G W, Nandi P, Saxe J M, et al. 1995. Prediction of rib fracture injury outcome by an artificial neural-network[J]. Journal of Trauma-Injury Infection & Critical Care, 39(5) : 915–924. |
| [${referVo.labelOrder}] | Grivas G, Chaloulakou A. 2006. Artificial neural network models for prediction of PM10 hourly concentrations, in the Greater Area of Athens, Greece[J]. Atmospheric Environment, 40(7) : 1216–1229. DOI:10.1016/j.atmosenv.2005.10.036 |
| [${referVo.labelOrder}] | 郭庆春, 何振芳. 2014. 基于人工神经网络的经济预测模型[J]. 计算技术与自动化, 2014, 33(4) : 132–136. |
| [${referVo.labelOrder}] | 韩力群. 2002. 人工神经网络理论、设计及应用[M]. 北京: 化学工业出版社: 11–55. |
| [${referVo.labelOrder}] | 何健, 肖保平. 2002. 成都市城市布局与大气环境质量的关系[J]. 铁道劳动安全卫生与环保, 2002, 29(5) : 208–210. |
| [${referVo.labelOrder}] | 黄思, 唐晓, 许文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(1) : 56–64. |
| [${referVo.labelOrder}] | Huo H, Yao Z, Zhang Y, et al. 2012. On-board measurements of emissions from diesel trucks in five cities in china[J]. Atmospheric Environment, 54 : 159–167. DOI:10.1016/j.atmosenv.2012.01.068 |
| [${referVo.labelOrder}] | Li G, Sang N. 2009. Delayed rectifier potassium channels are involved in SO2 derivative-inducedhippocampal neuronal injury[J]. Ecotoxicology and Environmental Safety, 72(1) : 236–241. DOI:10.1016/j.ecoenv.2007.11.015 |
| [${referVo.labelOrder}] | LI Z D, Han S N, Jiang J L, et al. 2013. Antitumor compound identification from Zanthoxylum bungeanum essential oil based on composition-activity relationship[J]. Chemical Research in Chinese Universities, 29(6) : 1065–1071. |
| [${referVo.labelOrder}] | 李璐, 刘永红, 蔡铭, 等. 2013. 基于气象相似准则的城市空气质量预报模型[J]. 环境科学与技术, 2013, 36(5) : 156–161. |
| [${referVo.labelOrder}] | 李嵩, 王冀, 张丹闯, 等. 2015. 大气PM2.5污染指数预测优化模型仿真分析[J]. 计算机仿真, 2015, 32(12) : 400–407. DOI:10.3969/j.issn.1006-9348.2015.12.086 |
| [${referVo.labelOrder}] | 刘闽, 王帅, 林宏, 等. 2014. 沈阳市冬季环境空气质量统计预报模型建立及应用[J]. 中国环境监测, 2014, 30(4) : 10–15. |
| [${referVo.labelOrder}] | 刘永红, 谢敏, 蔡铭, 等. 2011. 基于BP神经网络的佛山空气质量预报模型的研究[J]. 安全与环学报, 2011, 11(2) : 125–130. |
| [${referVo.labelOrder}] | 柳小桐. 2010. BP神经网络输入层数据归一化研究[J]. 机械工程与自动化, 2010(3) : 122–123. |
| [${referVo.labelOrder}] | Liu Y H, Zhu Q, Yao D, et al. 2015. Forecasting urban air quality via a back-propagation neural network and a selection sample rule[J]. Atmosphere, 6(7) : 891–907. DOI:10.3390/atmos6070891 |
| [${referVo.labelOrder}] | Moazami S, Noori R, Amiri B J, et al. 2016. Reliable prediction of carbon monoxide using developed support vector machine[J]. Atmospheric Pollution Research, 7(3) : 412–418. DOI:10.1016/j.apr.2015.10.022 |
| [${referVo.labelOrder}] | 孟晓艳, 王瑞斌, 杜丽, 等. 2011. 我国空气污染现状及对空气质量日报改进的思考[J]. 环境工程技术学报, 2011, 1(3) : 249–254. |
| [${referVo.labelOrder}] | Nava S, Lucarelli F, Amato F, et al. 2015. Biomass burning contributions estimated by ynergistic coupling of daily and hourly aerosol composition records[J]. Science of the Total Environment, 511(1) : 11–20. |
| [${referVo.labelOrder}] | Paschalidou A K, Karakitsios S, Kleanthous S, et al. 2011. Forecasting hourly PM10 concentration in Cyprus through artificial neural networks and multiple regression models:implications to local environmental management[J]. Environmental Science and Pollution Research, 18(2) : 316–327. DOI:10.1007/s11356-010-0375-2 |
| [${referVo.labelOrder}] | Pope C A Ⅲ, Burnett R T, Thun M J, et al. 2002. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution[J]. The Journal of the American Medical Association, 287(9) : 1132–1141. DOI:10.1001/jama.287.9.1132 |
| [${referVo.labelOrder}] | 秦喜文, 刘媛媛, 王新民, 等. 2016. 基于整体经验模态分解和支持向量机回归的北京市PM2.5预测[J]. 吉林大学学报 (地球科学版), 2016, 46(2) : 563–568. |
| [${referVo.labelOrder}] | Shaban K B, Kadri A, Rezk E, et al. 2016. Urban air pollution monitoring system with forecasting models[J]. IEEE Sensors Journal, 16(8) : 2598–2606. DOI:10.1109/JSEN.2016.2514378 |
| [${referVo.labelOrder}] | Sousa S I V, Martins F G, Alvim Ferraz M C M, et al. 2007. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations[J]. Environmental Modelling & Software, 22(1) : 97–103. |
| [${referVo.labelOrder}] | 田静毅, 范泽宣, 孙丽华. 2015. 基于BP神经网络的空气质量预测与分析[J]. 辽宁科技大学学报, 2015, 38(2) : 131–136. |
| [${referVo.labelOrder}] | Unal Y S, Toros H, Deniz A, et al. 2011. Influence of meteorological factors and emission sources on spatial and temporal variations of PM10 concentrations in Istanbul metropolitan area[J]. Atmospheric Environment, 45(31) : 5504–5513. DOI:10.1016/j.atmosenv.2011.06.039 |
| [${referVo.labelOrder}] | 王国胜, 郭联金, 董晓清, 等. 2015. 深圳市区空气污染的人工神经网络预测[J]. 环境工程学报, 2015, 9(7) : 3393–3399. DOI:10.12030/j.cjee.20150752 |
| [${referVo.labelOrder}] | 王小川, 史峰, 郁磊, 等. 2013. MATLAB神经网络43个案例分析[M]. : 1–3. |
| [${referVo.labelOrder}] | 魏璐, 朱伟军, 陈海山. 2009. 郑州市空气质量统计预报方法探讨[J]. 南京气象学院学报, 2009, 32(2) : 314–320. |
| [${referVo.labelOrder}] | 谢超, 马民涛, 于肖肖. 2015. 多种神经网络在华北西部区域城市空气质量预测中的应用[J]. 环境工程学报, 2015, 9(12) : 6005–6009. DOI:10.12030/j.cjee.20151257 |
| [${referVo.labelOrder}] | 熊德琪, 陈守煜. 1993. 城市大气污染物浓度预测模糊识别理论与模型[J]. 环境科学学报, 1993, 13(4) : 482–490. |
| [${referVo.labelOrder}] | 杨云, 付彦丽. 2016. 关于空气中PM2.5质量浓度预测研究[J]. 计算机仿真, 2016, 33(3) : 413–418. |
| [${referVo.labelOrder}] | 姚宁, 马青兰, 张晶, 等. 2015. 基于AGNES算法优化BP神经网络和GIS系统的大气污染物浓度预测[J]. 中国环境监测, 2015, 31(3) : 113–117. |
 2017, Vol. 37
2017, Vol. 37


