2. 浙江省水利厅, 杭州 310009
2. Department of Water Resources of Zhejiang Province, Hangzhou 310009
随着全球经济的发展及大城市和工矿区的建立, 大量化学物质排放进入空气、水体、土壤, 逐渐积累形成危及人类生存的污染物.其中, 污染物进入受纳水体的输移过程与水文特征、河流形态密切相关, 研究表明, 径流和潮位是影响污染物浓度的主要因素 (许丹等, 2010).鉴于河流流速、潮位和污染物输移之间内在的联系, 了解在径流和潮位共同作用下的污染物输移机理, 预测水体受污时间, 对于完善污染物输移机理的理论研究有着重要的科学意义, 同时对环境监督、水资源保护也具有重要的工程应用价值.
国内外研究较多涉及河流水动力条件及河流洪涝/径流方面的计算与预报, 也有研究涉及河流或海域中的水质指标的数学模型.刘坤等 (2009)通过MIKE软件中的EU (富营养化) 模块, 构建了适用于河流水质的一维、二维数学模型, 并用汉江和太湖水质监测资料对该数学模型进行了验证, 得到了与实测值较为吻合的运算结果.赵棣华等 (2003)通过有限体积法及黎曼近似解构建了符合长江江苏段感潮河段水流水质及地形特点的平面二维水流水质模型.朱效娟 (2007)选用WASP5通过Preissmann隐式差分格式建立河网的一维水动力和水质模型, 并应用于闸控感潮河网水环境的数值模拟.潘红波 (2007)选取长江南京潮汐河流段建立平面二维水动力模型, 分析其水流运动特征, 针对污染物构建基于拉格朗日法的随机游走模型, 分析了在典型水文条件下污染物的回荡规律及停留时间.Yang等 (2015)建立了表现极端干旱对长江口区域污染物输移过程影响的数学模型, 其计算结果与观测值表现出良好的一致性, 模型结果显示, 污染物输移过程与潮周期、潮流密切相关.Garcia等 (2002)利用垂向平均输移方程, 建立了用于计算浅水河口区域溶解氧浓度的数学模型, 并在Urdaibai河口地区的实践中取得了良好的效果.此外, 一系列的数值模型 (卢士强等, 2006;伍远康等, 2011;Petti et al., 2007;Cunha et al., 2006;Van Pagee et al., 1985;De Smedt et al., 1998;Sun et al., 2006;Gupta et al., 2004;Kachiashvili et al., 2007) 应用于模拟水环境中各种污染物的迁移过程.
杭州地处我国东部沿海, 整体经济发达, 城镇化水平较高, 城镇居民以集中式供水为主.生活饮用水的水质状况直接影响到人民群众的身体健康和生命安全.钱塘江是杭州第一大河, 杭州市全市80%以上的用水来自于钱塘江, 是杭州最主要的供水源头.钱塘江属于典型的感潮河流, 感潮河段潮差大、水动力条件复杂, 污染物随着涨潮落潮的过程产生往复, 对人类生产生活与河段生态系统的影响要远大于无潮河段.同时, 由于感潮河流污染的来源各式各样, 污染物也千差万别, 从实际情况及成本方面的考虑不可能监测所有指标, 且杭州地区频繁的人类活动增加了上游输入污染物的概率, 且在研究区域内有包括南星桥水厂在内的不少于15个水厂取水口.因此, 以感潮河段二维水动力水质数学模型进行数值模拟, 探求污染物迁移扩散, 对主要取水口段地表水质量进行安全预警 (之江站附近一段河段分布着杭州市水厂取水口), 利于减少突发事件时的用水安全、降低建设自动监测站的投入, 进而为取水用水安全进行预警.另一方面, 随着钱塘江上游工业生产力增长, 污染物排放已成为城市环境污染的一个重要来源, 经过感潮河流的作用, 污染物的控制与处理难度加大.于是, 对排放的污染物输移进行模型定性分析, 根据污染物排放的时间与空间分布变化, 研究感潮河段污染物迁移扩散, 可为政府合理制定污染源管理制度、城市布局及建设管理制度提供决策支持, 具有重要的理论意义和实用价值.本文基于潮流连续性方程、动量方程和污染物扩散方程, 构建研究区域感潮河段二维水动力和水质模型, 对钱塘江感潮河段上游监测到持续污染物输入的情况进行数值模拟.
2 研究方法 (Research methods) 2.1 水动力水质控制方程二维水动力水质控制方程采用基于Boussinesq假设和静水压力假定下雷诺平均的Navier-Stokes方程和污染物迁移扩散方程, 其中, 潮流连续性方程 (式 (1))、x向动量方程 (式 (2))、y向动量方程 (式 (3))、扩散方程 (式 (4)) 分别如下所示.包括粘性力和紊流应力的水平粘滞应力项Tij和水平扩散项Fc的计算分别如式 (5) 和 (6) 所示.
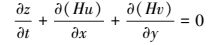
|
(1) |
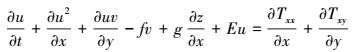
|
(2) |
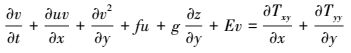
|
(3) |
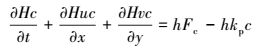
|
(4) |
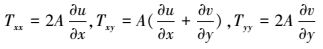
|
(5) |
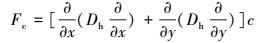
|
(6) |
式中, z为潮位 (m);h为基面下水深 (m);H为总水深 (m), H=h+z;u、v分别为x、y方向上垂线平均流速分量 (m·s-1);f为柯氏力系数 (rad·s-1), f=2ωsinψ, ω为地球自转角速度 (rad·s-1), ψ为纬度;g为重力加速度 (m·s-2);T为水平粘滞应力项 (m2·s-2);E为底床阻力参数 (s-1), 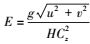
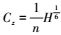
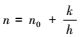
对于二维浅水方程组与扩散方程, 空间离散采用有限体积法 (FVM), 将计算区域细分为不重叠的三角形单元.方程组可表示为一般通用形式:
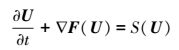
|
(7) |
式中, U代表守恒型物理向量;t为时间 (s);F表示通量向量;S则为源项.
利用Gauss原理在第i个单元质点采用积分法对方程 (7) 进行积分后, 再对边界用中点积分法进行积分, 得:
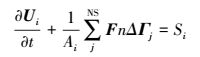
|
(8) |
式中, Ui、Si位于单元中心且分别表示第i个单元U和S的平均值;Ai为第i个单元Ω的面积;NS表示单元的边界数;ΔΓj代表第j个单元的长度.为避免数值震荡, 二维浅水方程组采用二阶TVD格式 (Darwish et al., 2003);而迁移方程则由TVD-MUSC格式来提供稳定性及减少振荡的影响.
对于二维模拟, 浅水方程组和扩散方程的时间离散有2种方法:低阶法和高阶法.由于笔者对研究区域进行了细致的三角网格划分, 网格数较多, 模型时间离散采用了计算时间较快的低阶Euler法.考虑方程的一般形式如式 (9) 所示, 低阶-显式Euler法, 具体离散格式表示为式 (10).为保证数值求解过程的稳定性, 采用的约束条件为CFL数小于0.8.
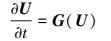
|
(9) |
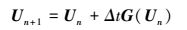
|
(10) |
式中, G为除时间偏导项外的通量向量.
3 潮流水质模型构建与验证 (Construction and validation of tidal and water quality model)富春江电站以下钱塘江感潮河段受径流和潮流共同影响, 水动力条件复杂, 水体中污染物一方面随着径流往下游迁移扩散, 另一方面会随着涨落潮往复, 对水质的影响较无潮河流要更加显著.本文选取钱塘江富阳至七堡段及三江口处汇流的支流浦阳江段作为研究河段, 具体见图 1.
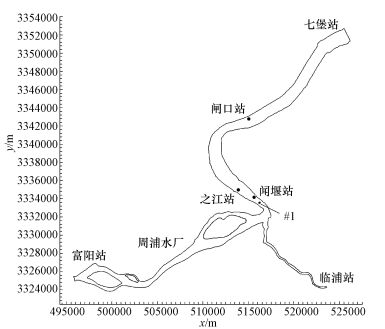 |
| 图 1 研究区域示意图 Fig. 1 Sketch map of the study area |
如图 1所示, 模型上边界取富阳站和临浦站, 下边界取七堡站, 上下游边界条件均采用浙江省水文局提供的实测潮位资料 (包括高锰酸盐指数数据).所选取验证资料的时间为:水动力部分验证资料为5月24日0:00至5月30日13:00, 高锰酸盐指数为5月24日0:00至5月30日13:00之江站实测资料.采用便于局部加密的三角网格剖分研究区域, 共有65401个网格, 34406个节点, 网格长度跨度小, 在10~50 m之间, 岸线处取50 m, 沙洲处取25 m, 临浦水文站开边界处取10 m.地形资料采用的是2010年10月的实测资料, 涡粘性系数取0.28, 糙率的取值范围为0.01~0.017, 下游糙率小, 上游糙率大, 采用随水深变化的形式, 模型所需糙率场见图 2.其中, 曼宁系数 (Manning) 为河床糙率倒数, 反映对水流阻力影响.
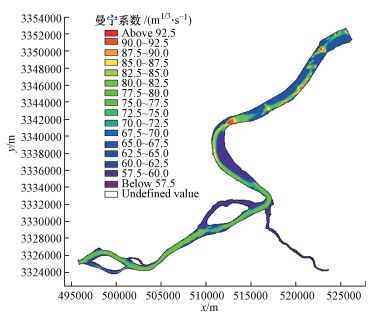 |
| 图 2 研究区域糙率场 Fig. 2 Roughness field of the study area |
水动力模块验证过程如图 3所示.图 3a、3b分别为闻堰站与闸口站实测潮位资料与模型模拟计算值的对比结果, 图 3c给出了流速的验证过程, 包括流速和流向.从图中可以发现, 模拟值与实测值吻合良好, 可为水质模型提供良好的水动力学条件.
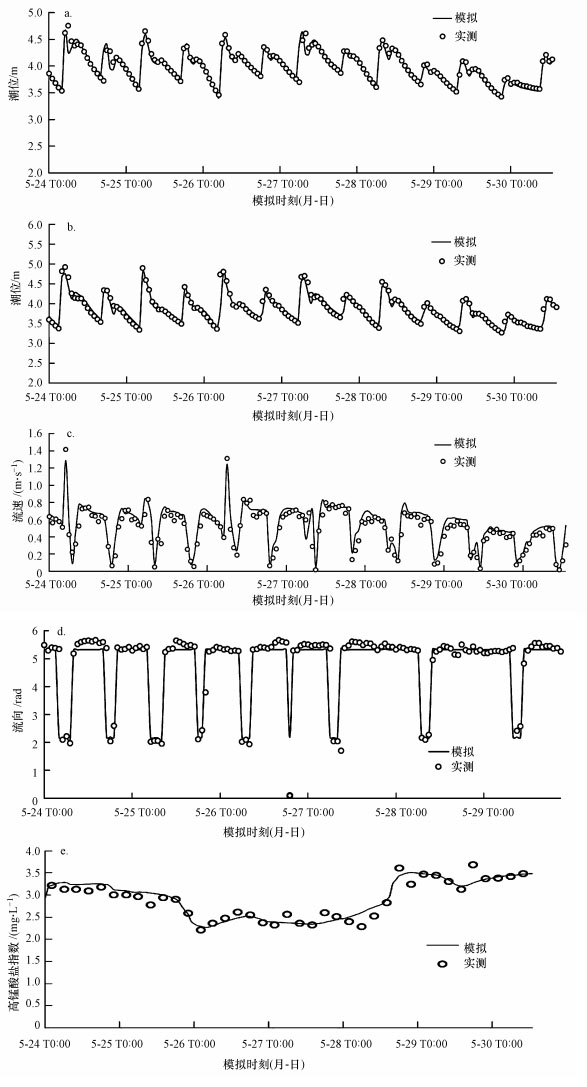 |
| 图 3 闻堰站潮位 (a)、闸口站潮位 (b)、1#点位流速 (c)、1#点位流向 (d) 和之江站污染物迁移及过程验证 (e) Fig. 3 Verification of tidal level processes at Wenyan station (a) and Zhakou station (b), the current velocity (c) and flow direction (d) of #1 and pollutant transport process at Zhijiang station (e) during May 24—30, 2011 |
在水动力验证的基础上对高锰酸盐指数进行验证, 模型模拟约经历4个潮周期达到模拟平衡, 具体为之江站实测资料与数值模拟计算所得高锰酸盐指数的对比, 如图 3d所示, 验证结果良好.确定的水平扩散系数取1.35 m2·s-1, 降解系数取10-6 s-1.模拟结果与实测值之间表现出良好的一致性, 为研究钱塘江河口感潮段水动力特征及污染物迁移扩散情况提供了有效的数学模型.
闻堰站位于浦阳江、富春江 (钱塘江上游段)、钱塘江三江交汇处略偏下游位置, 水动力条件比较特殊, 在模型验证过程中将其选为潮位验证过程的验证点;之江站与闻堰站相距较近 (相似点), 而闸口站则地处下游弯道拐口处, 且与闻堰站相距有一定的距离, 是潮位过程验证的另一点.1#点位于闻堰站稍偏上位置, 处在三江交汇处, 水流条件比较特别, 且同时又位于整个研究区域中间位置, 故而选取1#点作为流速验证点.之江站周围一段河段内分布着一些杭州市水厂取水口, 同时, 之江站的位置处在计算区域的中间段, 因此, 将其选为水质过程的验证点.经验证, 两站潮位过程的实测值与计算值吻合程度高, 且闻堰站与闸口站潮位波形相似, 闸口站较闻堰站更靠近河口, 其高潮位和低潮位都要较闻堰站高.流速则呈现往复流的情况, 由于受涨潮时长短落潮时长长的影响, 水流向上游流动时间短, 向下游流动时间长, 且涨急时刻流速激增.
4 模型计算与分析 (Model calculation and analysis)研究河段中闸口至周浦水厂段为饮用水源一级保护区, 河段内密布南星水厂、九溪水厂、萧山水厂、周浦水厂等一系列水厂的取水口, 地表水环境质量的好坏直接影响河段两岸人民的生产生活安全.本文模拟了富阳站监测到污染物输入的条件下, 考虑9种潮流和径流组合下污染物的迁移扩散情况.以之江站受到污染物影响的时间为切入点, 探求在9种流况组合下污染物迁移扩散对主要取水口段地表水环境质量的影响有着重要的意义.根据国家《地表水环境质量标准》确定模拟时间段内各边界高锰酸盐指数值, 富阳水文站测点取6.9 mg·L-1, 临浦水文站测点取4.1 mg·L-1, 七堡水文站测点取2.1 mg·L-1;模拟周期设置为3 d, 初始浓度场设置为0.洪季、枯季、平水月份依次选取2011年5月、12月、8月.
图 4模拟计算了之江站高锰酸盐指数在大、中、小潮, 以及洪季、枯季和平水月份9种流况组合下的迁移结果.处于枯季径流条件下, 大、中、小潮情况下, 数值模型模拟计算过程中之江站出现污染物的时间依次提前, 分别为模拟的第43、41、36 h;模拟结果表明,潮流对污染物向下游迁移扩散具有阻滞作用, 同时潮流作用越强, 其表现出的阻滞作用越明显.当径流处于平水月份条件下时, 之江站在大、中、小潮情况下污染物出现时间分别为第30、27、18 h;当径流处于洪季时, 其大、中、小潮情况下, 之江站污染物出现的时间分别为第52、42、48 h;平水月份径流条件下, 对大、中、小潮进行模拟, 发现潮流对污染物的向下游迁移的作用与枯季径流一致;同时通过平水月份与枯季的对比, 发现径流作用越强, 越有利于污染物向下游迁移扩散.
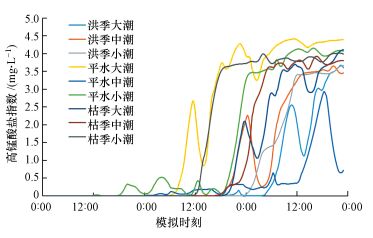 |
| 图 4 之江站高锰酸盐过程 Fig. 4 Permanganate process at Zhijiang station |
分析结果如下:① 本文利用三角网格对模型进行了细致的划分, 对模型所涉及的涡粘性系数、糙率、水平扩散系数、降解系数进行了率定, 利用省水文局提供的实测资料对计算模型进行了验证, 验证结果良好; ② 通过对平水月份径流和枯季径流之江站污染物出现时间的对比, 可以得出, 径流有利于污染物向下游扩散迁移, 且径流作用越强, 越有利于污染物向下游迁移扩散; ③ 在大潮作用下, 之江站一般最晚受到上游污染物影响, 中潮次之, 最早受到影响的是在小潮情况下, 说明在感潮河段, 由于受到下游潮流的影响, 对污染物往下迁移有一个阻滞作用, 且潮流越强阻滞作用越明显.
5 结论 (Conclusions)通过对钱塘江河口感潮段水动力场和污染物迁移过程的模型模拟, 发现污染物往下游迁移扩散的快慢受潮差和径流量大小的影响十分显著, 径流是驱动污染物往下游迁移扩散的主要动力, 径流量的增加有助于污染物向下游迁移, 当径流量增加到一定程度以后, 对污染物的稀释作用将会显著增强, 反而会使得下游受到污染物影响的时间相对较晚.而潮差对污染物迁移扩散表现出阻滞作用, 即潮流作用越强, 表现出的阻滞作用越明显.从水资源有效利用角度出发, 当上游监测到超标污染物输入后可采用数学模型计算, 确定何时停止在河段内取水, 改为从珊瑚沙等蓄淡水库取水更加合适.当上游水体中存在超标污染物输入的情况下, 从水资源饮用安全角度考虑, 为河段内确定恰当的取水时间提供有效的技术支持.同时, 本文构建的潮流水质模型为以后更加深入研究污染物在感潮河段迁移扩散机理提供模型模拟基础, 对于制定降低污染物迁移扩散对地表水环境质量影响措施具有现实意义.
| [${referVo.labelOrder}] | Cunha C L N, Rosman P C C, Ferreira A P. 2006. Hydrodynamics and water quality models applied to Sepetiba Bay[J]. Continental Shelf Research, 26(16) : 1940–1953. DOI:10.1016/j.csr.2006.06.010 |
| [${referVo.labelOrder}] | Darwish M S, Moukalled F. 2003. TVD schemes for unstructured grids[J]. International Journal of Heat and Mass Transfer, 46(4) : 599–611. DOI:10.1016/S0017-9310(02)00330-7 |
| [${referVo.labelOrder}] | De Smedt F, Mwanuzi F. 1998. Simulation of transport of toxic pollutants in surface waters[J]. Environmental Engineering Series, 3 : 303–312. |
| [${referVo.labelOrder}] | Garcia A, Revilla J A, Medina R, et al. 2002. A model for predicting the temporal evolution of dissolved oxygen concentration in shallow estuaries[J]. Hydrobiologia, 475-476(1) : 205–211. |
| [${referVo.labelOrder}] | Gupta I, Dhage S, Chandorkar A A, et al. 2004. Numerical modeling for Thane creek[J]. Environmental Modelling & Software, 19(6) : 571–579. |
| [${referVo.labelOrder}] | Kachiashvili K, Gordeziani D, Lazarov R, et al. 2007. Modeling and simulation of pollutants transport in rivers[J]. Applied Mathematical Modelling, 31(7) : 1371–1396. DOI:10.1016/j.apm.2006.02.015 |
| [${referVo.labelOrder}] | 刘坤, 杨正宇. 2009. MIKE软件在水体富营养化研究中的应用[J]. 给水排水, 2009, 35(Z1) : 456–458. DOI:10.3969/j.issn.1002-8471.2009.z1.133 |
| [${referVo.labelOrder}] | 卢士强, 林卫青, 徐祖信, 等. 2006. 苏州河环境整治二期工程水质影响数值模拟[J]. 长江流域资源与环境, 2006, 15(2) : 228–231. |
| [${referVo.labelOrder}] | Petti M, Bosa S. 2007. Accurate shock-capturing finite volume method for advection-dominated flow and pollution transport[J]. Computers & Fluids, 36(2) : 455–466. |
| [${referVo.labelOrder}] | 潘红波. 2007. 基于随机游走模式的感潮河流污染物迁移特征研究[D]. 南京: 河海大学 |
| [${referVo.labelOrder}] | Sun T, Tao J H. 2006. Numerical simulation of pollutant transport acted by wave for a shallow water sea bay[J]. International Journal for Numerical Methods in Fluids, 51(5) : 469–487. DOI:10.1002/(ISSN)1097-0363 |
| [${referVo.labelOrder}] | Van Pagee J A, Gerritsen H, de Ruijter W P M. 1985. Transport and water quality modelling in the southern North Sea in relation to coastal pollution research and control[J]. Water Science and Technology, 18 : 245–256. |
| [${referVo.labelOrder}] | 伍远康, 卢卫, 应聪惠, 等. 2011. 数值模拟在配水改善河道水质中的应用[J]. 水文, 2011, 31(3) : 56–59. |
| [${referVo.labelOrder}] | 许丹, 孙志林. 2010. 钱塘江河口突发污染物扩散数值模拟分析[J]. 浙江大学学报 (工学版), 2010, 44(9) : 1767–1772. |
| [${referVo.labelOrder}] | Yang Y, Chen X F, Li Y Y, et al. 2015. Modeling the effects of extreme drought on pollutant transport processes in the Yangtze River Estuary[J]. Journal of the American Water Resources Association, 51(3) : 624–636. DOI:10.1111/jawr.2015.51.issue-3 |
| [${referVo.labelOrder}] | 赵棣华, 李褆来, 陆家驹. 2003. 长江江苏段二维水流-水质模拟[J]. 水利学报, 2003(6) : 72–77. |
| [${referVo.labelOrder}] | 朱效娟. 2007. 受潮汐影响的河网水质模型的研究与应用[D]. 南京: 河海大学 |
 2017, Vol. 37
2017, Vol. 37


