2. 华南理工大学教育部工业聚集区域污染控制与修复重点实验室, 广州 510006;
3. 华南理工大学制浆造纸国家重点实验室, 广州 510006
2. The Key Lab of Pollution Control and Ecosystem Restoration in Industry Clusters, Ministry of Education, South China University of Technology;
3. State Key Laboratory of Pulp and Paper Engineering, South China University of Technology
废水厌氧处理在工业废水处理中越来越重要, 厌氧处理相对于好氧处理具有动力消耗小、污泥产量少、对氮和磷的需要量低, 可减少补充氮和磷营养的费用、厌氧消化可产生生物能等优点(Wijekoon et al., 2011).厌氧消化过程可简单地分为水解、发酵酸化、产乙酸、产甲烷4个阶段(贺延龄, 1998;成喜雨等, 2008;Demirel et al., 2002).从厌氧消化降解有机物的过程来看, 产甲烷菌对VFA的利用对厌氧消化至关重要.一方面厌氧消化的最终产物取决于产甲烷阶段;另一方面未被利用的VFA在一定程度上会抑制产甲烷菌的活性.Mawson等(1986)的研究表明, 当乙酸和丙酸浓度分别达到2000 mg·L-1和500 mg·L-1时, 产甲烷菌的活性受到了抑制.Xiao等(2013)研究了未降解的乙酸对厌氧消化过程中水解酸化菌和产甲烷菌的影响, 该研究表明水解酸化阶段可接受的最高未降解的乙酸浓度高于产甲烷阶段, 也即产甲烷菌对厌氧体系中未降解的乙酸浓度更敏感, 同时该研究结果指出当未降解的乙酸浓度在未超过阈值时乙酸的存在一定程度上提高了产甲烷菌的活性, 但当体系积累的乙酸达到阈值时极大地抑制了产甲烷菌的活性.需要指出的是, 不同的厌氧体系能忍受积累的VFA浓度是不同的, 这取决于厌氧消化降解的底物基质和厌氧体系的操作条件(张仁瑞, 1997).因此监控厌氧消化过程VFA浓度对于优化废水厌氧处理管理, 监控厌氧处理设施的运行具有指导意义.
针对VFA浓度的检测方法, 一直受到了高度的重视, 研究人员做了大量工作(Feitkenhauer et al., 2002;赵保全, 2008;Falk et al., 2015;姚崇龄, 2006).VFA浓度离线测定的方法主要有蒸馏法、滴定法、色谱法、比色法等(江伟, 2010), 然而这种基于电化学等离线分析耗时、滞后甚至费用昂贵, 不能满足快速变化的高负荷厌氧消化系统的在线监测需求.因此, 很有必要进一步研究VFA在线检测技术, 探究一个便捷、快速、低廉的检测策略.
基于人工神经网络、数理统计学等的软测量技术在废水处理过程中应用越来越广, 软测量模型适用于非线性系统建模, 可以应用快速并行处理算法从而大大提高辨识速度, 用于系统建模的方法很简单, 只需通过系统的输入和输出数据等特点, 使其对于水质变化频繁的废水生物处理仍然具有比较好的精度(李勇等, 2005;傅永峰, 2007;Huang et al., 2010).目前, 针对基于人工神经网络的软测量模型进行了大量研究, 其在废水处理中运用越来越广(Huang et al., 2016;黄明智, 2011).研究人员发现, 尽管基于人工神经网络的软测量模型表现较好, 但是由于神经网络是一种局部最优算法, 面对废水水质变化频繁亦存在过拟合和欠拟合, 且对于神经网络隐含层数和隐含层节点数的选择并无理论上的指导.SVM是近年来在机器学习领域中受到关注较多的一种基于统计学原理的新技术, 支持向量机(SVM, Support Vector Machine)作为一种高效简单的机器学习方法, 其在废水处理中的运用越来越受到关注(Selakov et al., 2014;Nieto et al., 2013;韩雯, 2012).刘博等(2014)提出一种基于PCA-LSSVM的厌氧废水处理系统出水VFA在线预测模型, 仿真结果表明在稳态环境下该模型具有很好的仿真能力, 然而元数据集加入非稳态数据后, 模型在非稳态环境下的仿真表现受到一定的干扰.
本文研究将基于SVM回归和分类模型构建软测量模型, 利用粒子群算法对模型参数寻优, 预测废水厌氧处理出水VFA浓度和COD去除率, 为监控和优化废水厌氧处理, 提高厌氧处理稳定性和效率提供指导.
2 材料及方法(Materials and methods) 2.1 实验装置与实验系统为获得不同进水条件下废水厌氧降解有机物出水VFA浓度以及处理的效果, 在实验室搭建一套废水厌氧处理系统.实验装置如图 1所示, 实验所用的IC厌氧反应器为有机玻璃制作, 高1272 mm, 内径200 mm, 有效容积25.1 L, 第一反应区与第二反应区的体积比为4:1, 废水通过BT600-2J型蠕动泵输送至反应器内, 水质参数在线监测系统由在线pH仪表(美国哈希公司, GLI MODEL33)、在线ORP仪表(GOLDTO TP560)、PT100温度传感器(u2p-010) 和湿式气体流量计(LML-1型)组成.反应器经过3个月成功启动, 接种污泥为广州某造纸厂IC反应塔厌氧颗粒污泥, 其总固体悬浮物(TSS)为112.56 g·L-1, 挥发性悬浮物(VSS)为132.04 g·L-1, VSS/TSS为0.852.
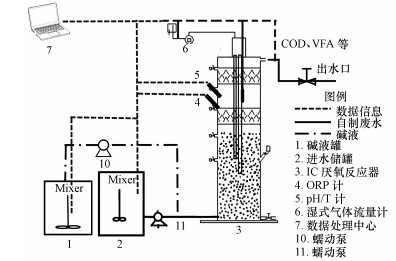 |
| 图 1 实验装置示意图 Fig. 1 Schematic diagram of the experimental apparatus |
实验废水采用自制废水, 实验废水将采用人工自配有机废水, 有机废水以葡萄糖、尿素、磷酸二氢钾按COD:N:P=200:5:1的比例配制, 同时加入1.8 mg·L-1 CaCl2·2H2O、0.5 mg·L-1 MgSO4、0.25 mg·L-1 CuSO4·5H2O、0.248 mg·L-1 CoCl2·6H2O、0.24 mg·L-1 FeCl3 ·5H2O、0.205 mg·L-1 ZnCl2、0.19 mg·L-1 NiCl2·6H2O、0.014 mg·L-1 H3BO4和0.009 mg·L-1 NH4MoO4·4H2O, 以保证厌氧微生物微量元素所需.反应器运行过程中通过变化进水有机负荷, 变化进水碱度的方式改变反应器进水条件和处理条件来获得不同条件下厌氧处理出水VFA浓度的变化以及出水VFA浓度与厌氧处理效果之间的联系.试验期间, pH值、ORP、温度由在线监测系统检测, COD采用重铬酸钾滴定法测定, 产气量采用湿式气体流量计测定, 产气组分采用气象色谱(A90气相色谱仪)外标法测定, VFA浓度及其组分含量采用气相色谱(A90气相色谱仪)外标法测定.
2.2 SVM模型SVM是由贝尔实验室的Vapnik及其研究小组于1995年在统计学习理论的基础上提出来的一类新型的机器学习方法(Vapnik et al., 1995).它开始是针对线性可分情况进行分析的, 后来对于线性不可分的情况, 通过使用非线性映射算法将低维输入空间线性不可分的样本映射到高维属性空间使其线性可分, 使得在高维属性空间采用线性算法对样本的非线性特性进行分析成为可能, 通过使用结构风险最小化准则在属性空间构造最优分割超平面, 使得机器学习得到全局最优化, 解决了学习问题, 对样本具有较好的泛化能力, 由于支持向量机的训练问题本质上是一个经典的二次规划问题, 避免了局部最优解, 有效地克服了维数灾难.
为了使SVM模型获得比较好的表现, 以下两点是至关重要的:① 为SVM模型选择核函数, 目前实际运用中比较常用的核函数有:高斯、多项式、样条、S形、RBF等核函数;② 为模型选择参数ε和C, 惩罚因子C又称正则化参数, 用以在训练中平衡机器学习的复杂性和经验风险(孙彤2013).
2.3 粒子群算法(pso算法)粒子群(Particle Swarm Optimization, PSO)算法是由Kennedy和Eberhart (2013)在人工生命研究的影响之下提出来的, 又模拟了鸟群在寻找食物过程中的集体迁徙行为, 提出了这种基于群体智能的演化计算方法.国内外研究表明pso算法广泛地用于优化统计学模型, 比如ANN模型(Dhanarajan et al., 2014), SVM模型(Nieto et al., 2016).原始的PSO算法的基本模型描述为:设在一个n维搜索空间中, 种群X={x1, x2, ……, xN}是由N个粒子构成, 其中第i个粒子所处的当前位置为x1={xi1, xi2, ……, xin}T, 其速度为v1={vi1, vi2, ……, vin}T, 该粒子的个体极值表示为P1={Pi1, Pi2, ……, Pin}T, 整个种群的全局极值表示为Pg={Pg1, Pg2, ……, Pgn}T, 按照粒子不断寻优的原理, 粒子xi的速度及位置更新公式如下所示
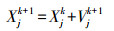
|
(1) |
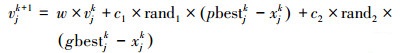
|
(2) |
式中, w是权重值, C1、C2为加速常数.rand1、rand2是随机函数, 作用是为了产生(0, 1) 的随机数.pso算法优化SVM模型的流程如图 2所示.
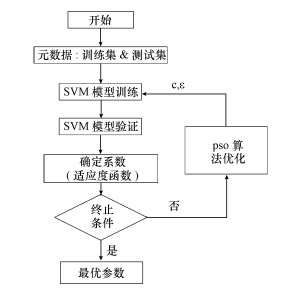 |
| 图 2 pso算法优化SVM模型流程 Fig. 2 Flowchart of pso algorithm optimized SVM model |
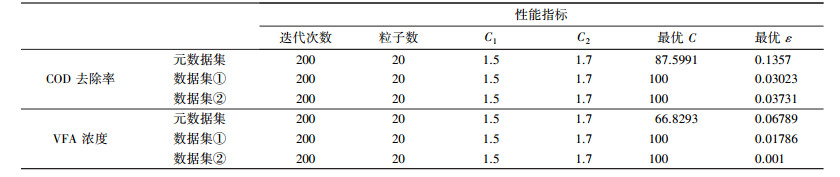
如前所述, 为得到模型较好的抗干扰能力、泛化能力和预测性能, 需要为模型选择核函数、核参数和正则化参数, 本文选取RBF函数作为SVM模型的核函数, 利用pso算法优化模型, 为SVM模型选择最优参数, 通过Matlab2015b软件平台建立模型.pso算法优化SVM模型得到的最优参数如表 1所示.
| 表 1 pso-svm模型参数 Table 1 Parameters of the pso algrithm and the best parameters of the SVM model |
整个基于pso-SVM的软测量模型流程如图 3所示.元数据分成测试集和训练集, 训练集用于建立模型, 测试集用于验证模型.将训练集数据用于pso-SVM-regression模型建模, 根据建模输出数据与训练集输出量的相对误差将训练集分成两个训练集(训练集① 及训练集②), 并标记训练集①、② 的元数据标签分别为1、-1;根据分成的两类训练集, 利用pso-SVM-classification模型将测试集分成两类, 从而将元数据分成了两个数据集;再利用SVM-Regression分别对数据集进行处理, 将经分类和未分类的模型表现进行分析总结.
 |
| 图 3 pso-SVM模型流程图 Fig. 3 Flowchart of hybrid PSO-SVM-based mod |
通过进水条件梯度变化, IC厌氧反应器成功运行60 d, 数据人工剔除明显异常值后利用拉依达准则剔除离群值, 共采集159组元数据.模型的输入量包括进水有机负荷, 出水pH、T、产气量及产气组分(甲烷、二氧化碳产量)、进水碱度、反应器ORP(氧化还原电位), 输出量包括出水总VFA浓度以及反应器COD去除率.
为确保模型的输入和输出值的统计分布是大致均匀的, 提高模型的运行精度以及速度, 需要将元数据集作归一化处理:
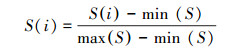
|
(3) |
式中, S(i)为数据集中的一组数据;min(S)为数据集中值最小的一组数据;max(S)为数据集中值最大的一组数据;
2.4.2 模型性能的评价指标为了直观地表达软测量模型的性能, 本文将选取以下评价指标来表征:
① 平均绝对百分比误差(Mean Absolute Percent Error,MAPE), MAPE是两组数据之间的所有相对误差的绝对值求和的平均值,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,能从整体上更好地反映预测值与实际值的偏差情况;
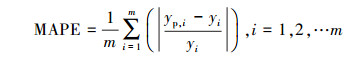
|
(4) |
② 均方根误差(Root Mean Square Error,RMSE)估计值与真值偏差的平方与检测次数n比值的平方根,RMSE主要是为了说明样本的离散程度;
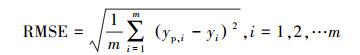
|
(5) |
③ 相关系数(correlation coefficient,R), R反映了估计值整体偏离实际值的强弱,R越接近于1则说明估计值与实际值越接近;
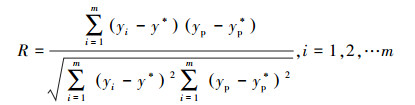
|
(6) |
(4) 相对误差(Relative Error,RE),RE表示绝对误差值与被测量值的真值之比,相对误差更能反映预测的可靠程度;
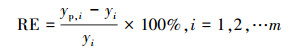
|
(7) |
以上各式中,y为实际值,y*为实际值均值,yp为预测值,yp*为实际值均值,m为样本数量.
3 结果与讨论(Results and discussion) 3.1 废水处理系统COD去除率与VFA浓度之间的联系图 4体现了厌氧处理系统COD去除率与出水VFA浓度之间的关系.分析图 4可得:随着出水VFA浓度的增大, 系统COD去除率越来越低;出水VFA浓度在0~250 mg·L-1之间时, 系统COD去除率大部分在75%以上;出水VFA浓度达到400 mg·L-1时, 系统COD去除率降低到65%;由此可见, 厌氧体系未降解的VFAs达到一定浓度时对厌氧系统微生物降解有机物产生了抑制.
 |
| 图 4 体系VFA浓度与COD去除率之间的联系 Fig. 4 Relationship between VFA concentration and COD removal rate |
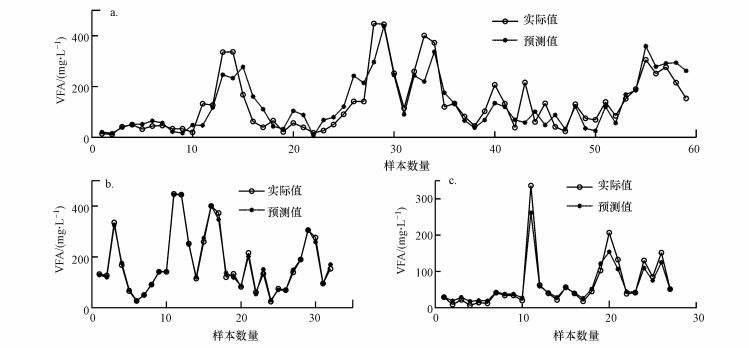
运用MATLAB的聚类多项式线性拟合工具体现VFA-COD去除率的线性关系.如图 4a所示, 一次多项式拟合VFA-COD去除率的表现来看, VFA-COD去除率之间的联系可用公式(4) 表示:
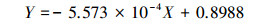
|
(8) |
一次多项式线性拟合线性相关性系数为0.7476, 均方根误差RMSE为0.4108;如图 4b所示, 三次多项式拟合VFA-COD去除率的表现来看, VFA-COD去除率之间的联系可用公式(5) 表示:

|
(9) |
一次多项式线性拟合线性相关性系数为0.8765, 均方根误差RMSE为0.1318.
目前经常用作废水厌氧消化效果的指标有产气量、COD去除率、pH、VSS等, 然而pH、产气量和VSS在指示厌氧消化过程中的突变往往过于滞后(Ahring et al., 1995).根据本文的结果可以看出, 体系累积的VFA与体系COD去除率存在一定的关系, 但VFA浓度累积到一定浓度时, 体系COD去除率下降的幅度越来越大, 体系VFA浓度可以成为厌氧消化的性能指标.
3.2 废水厌氧处理系统COD去除率预测仿真 3.2.1 元数据集分类结果数据集分类前, 数据集分为训练集和测试集, 其中训练集共100组数据, 测试集共59组数据.模型运行开始后, 根据模型针对训练集的输出量与实际值之间的误差将训练集平分为两个训练集(训练集① 及训练集②), 经过pso-SVM-classification模型将测试集分成两类测试集(测试集① 及测试集②), 至此, 元数据集分类成两类数据集:数据集①:训练集共50组数据、测试集共28组数据;数据集②:训练集共50组数据、测试集共31组数据.
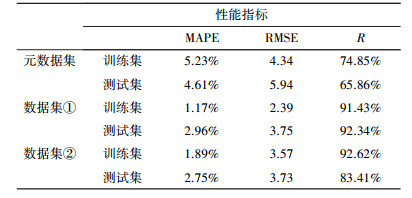
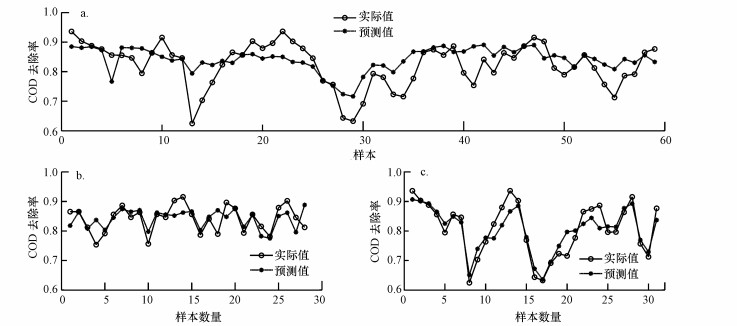
3.2.2 模型仿真结果废水厌氧处理系统COD去除率预测仿真结果见表 2及图 5.由表 2分析模型训练过程中的性能指标, 分类之后模型的线性相关性R由74.85%提高到91.43%和92.62%, 在元数据集分类之后模型训练过程中的其他指标均有提升, 由此可知分类之后模型获得了输入量与输出量之间更为明确的模糊关系.对比分类前后的模型表现, 通过对比图 5a与图 5b、图 5c, 模型在数据集分类后的性能表现提升较大, 虽然在水质变化较大时, 模型的表现不够理想, 但是相对于分类前模型表现提升较大.分类之前, 模型的各性能指标(测试集)RMSE为5.94, MAPE为4.61%, 相关性R为65.86%;分类之后, 数据集① 及数据集② 的性能指标分别为:RMSE为3.75、3.73, MAPE为2.96%、2.75%, 相关性R为92.34%、83.41%.图 6表示的是模型仿真结果与实验值的相对误差, 模型分类前相对误差最大为27.10%, 分类后相对误差最大分别为11.84%、11.95%.
 |
| 图 5 pso-SVM模型对COD去除率仿真结果 Fig. 5 Prediction results of the models for COD removal rate |
| 表 2 厌氧体系COD去除率模型预测性能 Table 2 Predicting performance of modes for COD removal rate |
 |
| 图 6 pso-SVM模型对COD去除率仿真相对误差 Fig. 6 Relative errors of testing by pso-SVM model for COD removal rate |
数据集分为训练集和测试集, 其中训练集共100组数据, 测试集共59组数据.模型运行开始后, 根据模型针对训练集的输出量与实际值之间的误差将训练集平分为两个训练集(训练集① 及训练集②), 经过pso-SVM-classification模型将测试集分成两类测试集(测试集① 及测试集②), 至此, 元数据集分类成两类数据集:数据集①:训练集共50组数据、测试集共32组数据;数据集②:训练集共50组数据、测试集共27组数据.
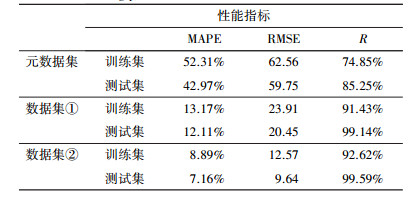
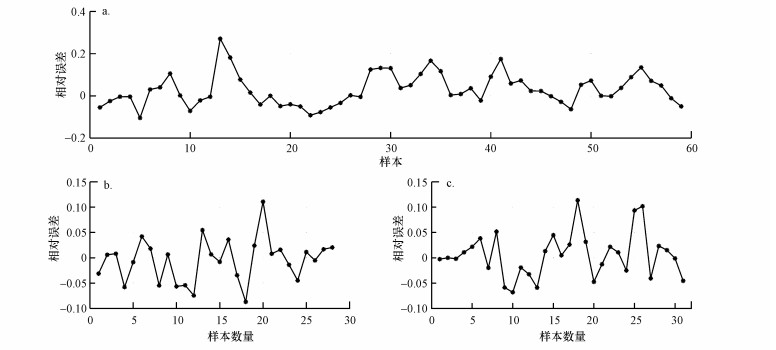
3.3.2 模型仿真结果废水厌氧处理系统VFA浓度预测仿真结果见表 2及图 7.通过分析图 7a, pso-SVM模型对废水厌氧处理系统VFA浓度具有较好的预测仿真能力, 但是当水质变化较大时, 模型存在欠拟合的问题, 局部表现较差.对比分类前后的模型表现, 通过对比图 7a与图 7b、图 7c, 模型在数据集分类后的性能表现提升较大.分类之前, 模型的各性能指标(测试集)RMSE为59.75, MAPE为42.97%, 相关性R为85.25%;分类之后, 数据集① 及数据集集② 的性能指标分别为:RMSE为20.45、9.64, MAPE为12.11%、7.16%, 相关性R为99.14%、99.59%.图 8表示的是模型仿真结果与实验值的相对误差, 模型分类前相对误差最大为179.47%, 分类后相对误差最大分别为21.91%、165.85%.从图 8可以看出, 元数据集分类后模型对个别样本单元的预测表现依然不够理想, 若要针对每个样本集获得更为精确的预测结果, 需要优化模型的核函数、分类策略等(Cao et al., 2016), 这也是未来的研究方向.
 |
| 图 7 pso-SVM模型对VFA浓度预测结果 Fig. 7 Prediction results of the models for VFA concentration |
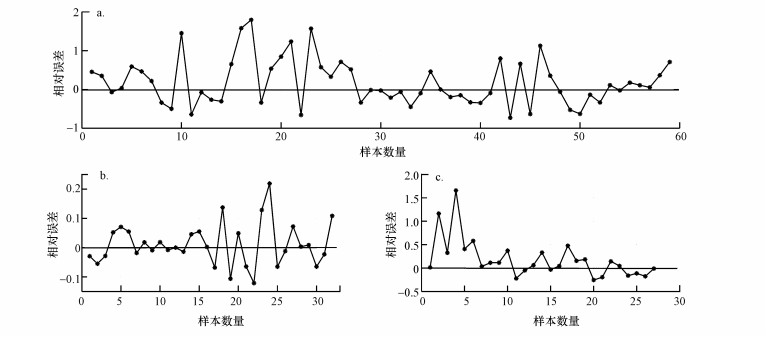 |
| 图 8 pso-SVM模型对VFA浓度仿真相对误差 Fig. 8 Relative errors of testing by pso-SVM model for VFA concentration |
| 表 3 厌氧体系VFA浓度模型预测性能 Table 3 Predicting performance of modes for VFA concentration |
1) 元数据集分类之前, pso-SVM模型对废水厌氧处理体系COD去除率及出水总VFA浓度的仿真表现较好, 测试样本的整体预测数据与实际数据的相关系数分别为65.86%, 85.25%.
2) 为提升模型的表现加入分类策略将元数据集分成两类(数据集① 和数据集②), 对比分类前后仿真结果, 数据集数据量达到一定量后, 通过加入分类策略可以较大地提升模型的表现, 模型预测系统COD去除率测试样本数据相关系数分别为92.34%、83.41%;模型预测系统出水总VFA浓度测试样本数据相关系数分别为99.14%、99.59%.
3) 引入分类策略对元数据集进行有效分类, 基于pso-SVM的软测量模型可为监控、优化和理解厌氧消化过程提供指导.
| [${referVo.labelOrder}] | Ahring B K, Sandberg M, Angelidaki I. 1995. Volatile fatty acids as indicators of process imbalance in anaerobic digestors[J]. Applied Microbiology and Biotechnology, 43(3): 559–565. DOI:10.1007/BF00218466 |
| [${referVo.labelOrder}] | Cao H L, Xin Y, Yuan Q X. 2016. Prediction of biochar yield from cattle manure pyrolysis via least squares support vector machine intelligent approach[J]. Bioresource Technology: 202158–164. |
| [${referVo.labelOrder}] | Clerc M, Kennedy J. 2002. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions Evolution Compution, 6(1): 58–73. DOI:10.1109/4235.985692 |
| [${referVo.labelOrder}] | Cortes C, Vapnik V. 1995. Support-Vector networks[J]. Machine Learning, 20(3): 273–297. |
| [${referVo.labelOrder}] | 成喜雨, 庄国强, 苏志国, 等. 2008. 沼气发酵过程研究进展[J]. 过程工程学报, 2008, 8(3): 607–615. |
| [${referVo.labelOrder}] | Demirel B, Yenigün O. 2002. The Effects of Change in Volatile Fatty Acid (VFA) Composition on Methanogenic Upflow Filter Reactor (UFAF) Performance[J]. Environmental Technology, 23(10): 1179–1187. DOI:10.1080/09593332308618336 |
| [${referVo.labelOrder}] | Dhanarajan G, Mandal M, Sen R. 2014. A combined artificial neural network modeling-particle swarm optimization strategy for improved production of marine bacterial lipopeptide from food waste[J]. Biochemical Engineering Journal, 84: 59–65. DOI:10.1016/j.bej.2014.01.002 |
| [${referVo.labelOrder}] | 傅永峰. 2007. 软测量建模方法研究及其工业应用[D]. 杭州: 浙江大学. 2-21 |
| [${referVo.labelOrder}] | Falk H M, Reichling P, Andersen C, et al. 2015. Online monitoring of concentration and dynamics of volatile fatty acids in anaerobic digestion processes with mid-infrared spectroscopy[J]. Bioprocess and Biosystems Engineer, 38(2): 237–249. DOI:10.1007/s00449-014-1263-9 |
| [${referVo.labelOrder}] | Feitkenhauer H, Von Sachs J, Meyer U. 2002. On-line titration of volatile fatty acids for the process control of anaerobic digestion plants[J]. Water Research, 36(1): 212–218. DOI:10.1016/S0043-1354(01)00189-0 |
| [${referVo.labelOrder}] | Huang M Z, Han W, Wan J Q, et al. 2016. Multi-objective optimisation for design and operation of anaerobic digestion using GA-ANN and NSGA-Ⅱ[J]. Journal of Chemical Technology and Biotechnology, 91(1): 226–233. DOI:10.1002/jctb.4568 |
| [${referVo.labelOrder}] | 韩雯. 2012. 污水处理控制系统设计与软测量建模研究[D]. 西安: 西安建筑科技大学. 1-5 |
| [${referVo.labelOrder}] | 贺延龄. 1998. 废水的厌氧生物处理[M]. 北京: 中国轻工业出版社: 42–54. |
| [${referVo.labelOrder}] | 黄明智. 2011. 废水处理系统水质特征动态分析的混合智能控制研究[D]. 广州: 华南理工大学 |
| [${referVo.labelOrder}] | Huang M Z, Wan J Q, Ma Y W, et al. 2010. A fast predicting neural fuzzy model for on-line estimation of nutrient dynamics in an anoxic/oxic process[J]. Bioresource Technology, 101: 1642–1651. DOI:10.1016/j.biortech.2009.08.111 |
| [${referVo.labelOrder}] | 江伟. 2010. 废水中低浓度挥发性脂肪酸测定方法及其应用研究[D]. 重庆: 重庆大学. 1-10 http://cdmd.cnki.com.cn/Article/CDMD-10611-2010217680.htm |
| [${referVo.labelOrder}] | Mawson A J, Earle R L, Larsen V F. 1986. Degradation of acetic and propionic acids in the methane fermentation[J]. Water Research, 25: 1549–1554. |
| [${referVo.labelOrder}] | 李勇, 邵诚. 2005. 软测量技术及其应用与发展[J]. 工业仪表与自动化装置, 2005, 5(5): 5–11. |
| [${referVo.labelOrder}] | 刘博, 万金泉, 黄明智, 等. 2015. 基于PCA-LSSVM的厌氧废水处理系统出水VFA在线预测模型[J]. 环境科学学报, 2015, 35(6): 1768–1778. |
| [${referVo.labelOrder}] | Nieto P J G, Combarro E F, del Coz Díaz J J, et al. 2013. A SVM-based regression model to study the air quality at local scale in Oviedo urban area (Northern Spain):A case study[J]. Applied Mathematics and Computation, 219(17): 8923–8937. DOI:10.1016/j.amc.2013.03.018 |
| [${referVo.labelOrder}] | Nieto P J G, García Gonzalo E, Fernández J R A, et al. 2016. A hybrid PSO optimized SVM-based model for predicting a successful growth cycle of the Spirulina platensis from raceway experiments data[J]. Journal of Computational and Applied Mathematics, 291: 293–303. DOI:10.1016/j.cam.2015.01.009 |
| [${referVo.labelOrder}] | Selakov A, Cvijetinovic' D, Milovic' L, et al. 2014. Hybrid PSO-SVM method for short-term load forecasting during periods with significant temperature variations in city of Burbank[J]. Applied Soft Computing, 16: 80–88. DOI:10.1016/j.asoc.2013.12.001 |
| [${referVo.labelOrder}] | 孙彤. 2013. 基于最小二乘支持向量机的高炉铁水温度预测模型的研究[D]. 包头: 内蒙古科技大学. 35-43 |
| [${referVo.labelOrder}] | Wijekoon K C, Visvanathan C, Abeynayaka A. 2011. Effect of organic loading rate on VFA production, organic matter removal and microbial activity of a two-stage thermophilic anaerobic membrane bioreactor[J]. Bioresource Technology, 102(9): 5353–5360. DOI:10.1016/j.biortech.2010.12.081 |
| [${referVo.labelOrder}] | Xiao K K, Guoa C H, Zhoua Y, et al. 2013. Acetic acid inhibition on methanogens in a two-phase anaerobic process[J]. Biochemical Engineering Journal, 75: 1–7. DOI:10.1016/j.bej.2013.03.011 |
| [${referVo.labelOrder}] | 姚崇龄, 张阿卜, 关键生. 2006. 神经模糊建模在厌氧消化过程中的应用[J]. 仪器仪表学报, 2006, 27(6): 1122–1124. |
| [${referVo.labelOrder}] | 张仁瑞. 1997. V FA作为厌氧生物学指标的可行性研究[J]. 青岛建筑工程学院学报, 1997, 18(2): 51–55. |
| [${referVo.labelOrder}] | 赵全保. 2008. 厌氧反应器的运行与在线监测[D]. 合肥: 中国科学技术大学. 16-6 |
 2017, Vol. 37
2017, Vol. 37