2. 桂林航天工业学院能源与建筑环境学院, 桂林 541004
2. School of Energy and Building Environment, Guilin University of Aerospace Technology, Guilin 541004
有文献指出, 目前全球和区域大气气溶胶输送模式和空气质量评估模式等研究与应用中, 对气溶胶湿清除率计算的准确性会影响到这些模式对气溶胶输送过程估计的准确性(Baklanov et al., 2001; 罗淦等, 2006; Henzing et al., 2006; Sportisse, 2007; 王瑛等, 2014).从气溶胶降雨清除率(或清除系数)的估计模型看, 雨滴与气溶胶粒子间的碰撞机理和捕集效率的正确描述是准确估计气溶胶降雨清洗系数的前提(Jung et al., 2001; 赵海波等, 2005; Croft et al., 2009; Bae et al., 2010; Zhang et al., 2013; Wang et al., 2014).
迄今为止, 已有很多研究讨论了雨滴或水滴对气溶胶捕集效率的估计问题, 如Greenfield(1957)在分析降雨过程中气溶胶湿清除机理时, 认为粒子直径为0.1~2.0 μm区间的粒子最难被雨滴清除, 通常称之为“Greenfield gap”, 但Greenfield并未对各种捕集机理所产生的效率做计算.Langmuir(1948)分别在粘性流(雨滴Reynolds数Re<1) 和势流(Re≫1) 情形下, 数值求解了这两种流型下雨滴对粒子的惯性捕集效率, 给出了简单的效率估算公式; 在讨论与气溶胶降雨清除有相似物理背景的湿式除尘机理时, Prem等(1978)在势流模型下分析了气溶胶粒子在水滴表面的惯性碰撞、布朗扩散及拦截效应等多机理作用下的耦合捕集行为; Beard等(1974)则讨论了中等Re数雨滴对粒子的惯性捕集效率, 但忽略了雨滴对粒子的拦截效应.此外, 在经典雨滴捕集机理的基础上, 许多研究者还分析了雷雨过程中电效应对粒子捕集的影响(Grover et al., 1977; Wang et al., 1978; Bae et al., 2014); Slinn(1977)在理论分析基础上耦合部分实验数据给出了目前广泛应用于云下气溶胶粒子雨洗系数估计的雨滴捕集效率公式, 但该公式仅考虑了粒子的惯性碰撞、拦截和扩散3种主要捕集机理.最近, 有研究者开始关注一些新的物理机制, 如大气湍流效应、雨滴尾部涡流及液滴绕流时的非稳态行为对粒子捕集可能产生的影响(华凤娇等, 2013; Quérel et al., 2014; Wang et al., 2016).然而, 上述研究中粒子的重力作用一般视为可忽略动力学因素, 而未在降雨清除动力学分析中加以考虑.此外, Beard等(1974)认为对实际大气气溶胶降雨清除的分析可采用硬球模型近似描述雨滴附近的流体绕流特征, 即忽略雨滴表面流体的滑移效应.实际上, 上述结论是在大尺度雨滴背景下给出的, 而对于小雨滴(Re<1) 捕集气溶胶粒子过程, 雨滴表面流体滑移效应和重力作用是否为可忽略因素, 并未做可靠的分析.此外考虑到在云内气溶胶降雨清除过程中, 存在大量几十微米的微细雨滴(亦称云滴) (Pruppacher et al., 1997; Wang, 2013), 因此, 讨论这一微小尺度雨滴对气溶胶的清除机理同样具有重要的应用价值.
本文将以Hadamard-Rybczynski流作为低Reynolds数(Re<1) 雨滴表面粒子捕集动力学分析的背景流场(Wang, 2013), 采用拉格朗日法(粒子轨迹追踪法)求解粒子在惯性碰撞、拦截及重力作用下的耦合捕集效率.试图通过严格的数值计算, 定量给出雨滴表面流体滑移效应和粒子重力作用对粒子捕集行为的影响, 为进一步分析气溶胶雨洗动力学机制提供理论参考.
2 物理模型(Physical model) 2.1 粒子运动方程及求解如图 1所示, 考虑雨滴在重力作用下以终端速度U∞作匀速垂直下落运动.均匀分布于大气中的气溶胶粒子随气流运动并绕过雨滴时, 在惯性碰撞、拦截和重力作用下与雨滴发生碰撞而被捕集.为简化动力学求解过程, 忽略雨滴之间的凝并和冷凝/蒸发等动力学行为, 认为雨滴降落过程中其尺度始终不变, 并保持为规则球形; 假定粒子相为稀薄相, 即粒子的存在不影响雨滴周围的气流流场; 进入计算域的气溶胶粒子视为具有相同密度的实心球体; 假定雨滴与环境大气间的温度相等, 粒子与雨滴均为电中性状态, 故可忽略粒子热泳、扩散泳及静电捕集作用; 忽略实际降雨过程中大气湍流效应对气溶胶粒子-雨滴系统动力学行为的影响.
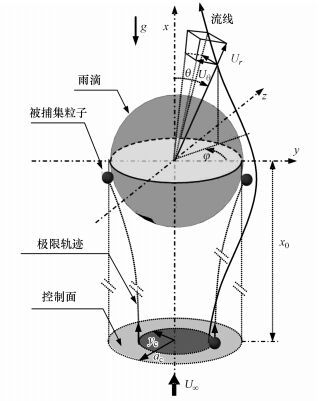 |
| 图 1 雨滴捕集粒子模型 Fig. 1 Simulated model for particles capture by a raindrop |
根据上述设定, 将坐标原点置于雨滴中心, 则气流和气溶胶粒子将以与重力相反的方向绕雨滴运动, 如图 1所示.单个气溶胶粒子的受力平衡方程可表示为式(1)(Hinds, 2012)
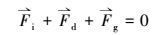
|
(1) |
式中, 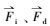
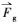
由于本文考虑的惯性粒子(dp>10 μm)所受的流体曳力满足Stokes阻力定律(Hinds, 2012), 考虑到绕雨滴流场具有轴对称性, 故仅需考虑粒子在r和θ方向所受的流体曳力(式(2))(Beizaie et al., 1980; Hinds, 2012).
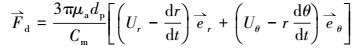
|
(2) |
粒子在r和θ方向所受惯性力可表示为式(3)(Beizaie et al., 1980).

|
(3) |
由于假定雨滴作垂直下落, 故粒子所受重力仅存在r和θ方向的分量, φ方向分量为零(式(4)).
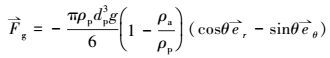
|
(4) |
式(2)~(4) 中: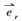
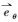
将上述3种作用力的表达式代入粒子受力平衡方程式(1), 并引入下列无量纲参量
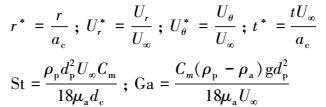
|
则气溶胶粒子动力学方程(1) 最终可改写为如下无量纲标量形式

|
(5a) |
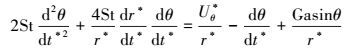
|
(5b) |
式中, Ur*和U∞*分别表示流体在r和θ方向的无量纲速度分量, 这是由于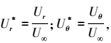

|
(6) |
式中, λ为空气分子平均自由程, 根据分子运动论的相关理论(Yates et al., 2007)
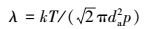
|
(7) |
式中, k为Boltzmann常数, k = 1.38×10-23 J·K-1; T为热力学温度(K); p为空气压强(Pa); da为空气分子直径(m).
采用数值计算求解粒子运动轨迹时, 其运动起始点设置于远离雨滴中心的控制面上(控制面大小与雨滴投影面相等), 见图 1.由于气溶胶粒子在大气中存在终端沉降速度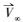
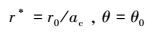
|
(8a) |
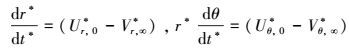
|
(8b) |
式中, r0和θ0分别为粒子运动的初始位置坐标; Ur, 0*(=Ur, 0/U∞)和Uθ, 0*(=Uθ, 0/U∞)分别为流体在(r0, θ0)处的无量纲速度量; Vr, ∞*(=Vr, ∞/U∞)和Vθ, ∞*(=Vθ, ∞/U∞)分别为粒子终端下落速度在r和θ方向的无量纲速度分量.
给定粒子运动的初始条件, 则采用四阶Runge-Kutta格式对式(5) 作数值积分(李庆扬, 2000), 即可获得粒子的运动轨迹.
已有实验研究结果指出, 无论是亲水性或疏水性粒子, 一旦粒子与雨滴发生碰撞行为, 则该粒子均可被雨滴捕集(Stulov et al., 1978; Wang et al., 1983), 故本文中粒子捕集的条件为粒子与雨滴表面发生接触.考虑到低Re数雨滴绕流流场不存在尾部涡流, 当粒子运动至雨滴背风面处, 则该粒子将继续远离雨滴运动而不会被捕集, 故终止其轨迹计算.因此, 粒子轨迹迭代计算停止的判据表示为
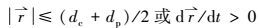
|
(9) |
式中, 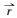
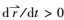
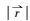
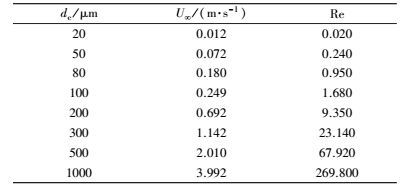
为获得雨滴对气溶胶粒子捕集效率的准确表达, 需要合理地描述雨滴周围的气体流动状态.由于雨滴的终端下落速度大小决定了Re数, 故也将对应着不同的绕流流型.在云下雨洗研究中, 对雨滴终端下落速度的估计有多种方法(Wang, 2010; Duhanyan et al., 2011), 本文采用Beard公式来估计雨滴的终端速度(Beard et al., 2010).表 1给出了一些典型尺寸雨滴的终端速度及对应的Reynolds数的值, 表中Re=dcU∞/μa.
| 表 1 雨滴终端下落速度及Re数 Table 1 Raindrop terminal velocities and Reynolds numbers |
通常认为, 雨滴Re数小于1时, 粘性流模型可近似描述雨滴附近流体的绕流特征(Levich, 1962), 据表 1的计算结果, dc≤80 μm雨滴的Re数小于1, 考虑到dc=100 μm雨滴的Re数仍与1接近, 故本文将讨论的小雨滴尺度范围定义为dc ≤ 100 μm.此时绕雨滴的流场可采用Hadamard-Rybczynski流描述(以下简称H-R流场), 原因是该流场较好地描述了雨滴表面的流体滑移效应(Wang, 2013).
在图 1所示的球坐标下, 考虑问题的对称性, H-R流场在r和θ方向的速度分量形式为(Wang, 2013)
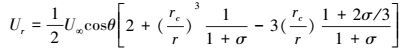
|
(10a) |
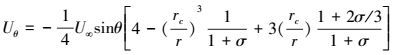
|
(10b) |
式中, σ=μa/μc, 表示空气动力黏度与雨滴黏度之比.注意到σ=0时, 式(10) 即退化为硬球绕流流场(Levich, 1962).
2.3 雨滴捕集效率计算雨滴捕集效率(E)通常定义为单位时间内被雨滴捕集的气溶胶粒子数与通过图 1所示控制面内的粒子数的比值(Langmuir, 1948; Beard et al., 1974; Prem et al., 1978).在忽略粒子布朗随机运动下, 若给定粒子的初始条件, 则其运动轨迹是确定的.此时, 定存在一条区分粒子能否被捕集的临界轨迹, 即极限轨迹(图 1).令极限轨迹在控制面上构成一个半径为yc圆面, 则通过该圆面的粒子将被捕集, 其余粒子则绕过雨滴而未捕集.根据捕集效率定义, E可由式(11) 计算出.
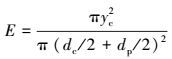
|
(11) |
可见, 应用轨迹方法分析粒子捕集效率的关键是获得粒子的极限轨迹.本文采用二分查找搜寻算法(Method of Bisection)快速获得粒子的极限轨迹.计算流程如下:
考虑直径为dp的粒子第一条轨迹起点y值记为y1.为方便极限轨迹计算, 取y1≥(dc+dp)/2, 即保证第1条粒子轨迹未与雨滴碰撞, 第2条粒子轨迹起点取为y2=(y1-0)/2 = y1/2.经计算, 若第二条轨迹与雨滴发生碰撞, 则第3条轨迹计算起点y3= y2 + (y1-y2)/2.反之, 则y3= (y2 -0)/2 = y2/2, 如此迭代直至获得满足计算精度要求的极限轨迹.
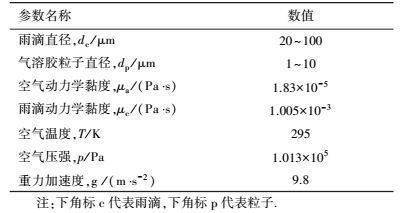
3 结果与讨论(Results and discussion)如前所述, 本文讨论雨滴表面流体滑移效应和重力作用对气溶胶粒子捕集效率的影响.为获得明确的分析结果, 假定粒子所处环境为定温、定压条件, 且空气及雨滴的动力学黏度为常数.数值计算中采用的物理参量列于表 2中.
| 表 2 数值计算中所采用的物理参量 Table 2 Values of parameters used in numerical calculations |
根据上述数值分析模型可知, 粒子轨迹计算需先确定粒子释放面(即控制面)距雨滴中心的距离x0(见图 1).已有文献指出(Prem et al., 1978; Leong et al., 1982), x0取值大小对粒子捕集效率的影响较大.根据雨滴捕集效率定义, 粒子初始位置应在距离雨滴中心无穷远处(x0→∞), 以完全消除雨滴对流场的畸变影响.然而在实际数值计算中, 则需根据计算精度要求合理选取x0.本文采用先后两次x0取值下雨滴捕集效率的相对误差小于1%为计算精度判据, 即
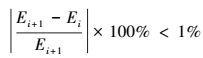
|
(12) |
式中, Ei+1和Ei分别x0, i+1和x0, i对应的效率计算值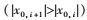
粒子轨迹计算时间步长的取值对捕集效率计算结果的精确性亦有影响.本文中无量纲时间步长t*(t*=tU∞/ac)以先后两次步长取值下, 捕集效率相对误差小于1%作为取值合理性的判据.经数值验证t*=0.005可满足计算精度要求.
3.1 数值模型可靠性验证已有研究者讨论了硬球捕集体面上粒子的纯惯性捕集效率(EI)与纯拦截捕集效率(ER)(Fuchs, 1954; Friedlander 1957; Fonda et al., 1960).这些结果可用于本文数值程序的可靠性验证, 为取得与已有结果相一致的计算参数条件, 先忽略粒子的重力作用和雨滴表面流体的滑移效应, 应用本文的数值程序分别求解了硬球表面粒子的纯惯性捕集效率和纯拦截捕集效率, 并与已有结果做了对比, 见图 2.
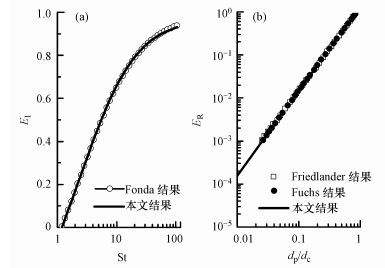 |
| 图 2 本文数值计算与其他研究结果的比较 Fig. 2 Comparisons between the present results and previous studies |
图 2a的结果表明, 在只考虑纯惯性捕集机理时, 本文给出的效率计算值与Fonda等(1960)的结果十分吻合, 只在较高St数时, 略低于Fonda的计算值.图 2b给出了本文数值计算的纯拦截捕集效率值与Friendlander(1957)和Fuchs(1964)理论求解结果的比较.可以看出, 本文数值给出的纯拦截效率值与理论求解结果完全一致.至此, 验证结果已说明本文的数值程序可用于对粒子运动轨迹的精确计算和雨滴对粒子捕集效率的准确估计.
3.2 雨滴表面流体滑移及粒子重力对捕集效率的影响现利用上述模型讨论低Re数雨滴表面流体滑移效应及重力作用对粒子捕集效率的影响.图 3给出了直径为50 μm雨滴在有无滑移作用下的粒子捕集效率曲线, 粒子ρp=1000 kg·m-3.图中曲线1表示无滑移但有重力作用时的捕集效率随粒径的变化关系; 曲线2表示有滑移且有重力作用时的粒子捕集效率变化关系; 曲线3则表示无滑移亦无重力作用时的粒子捕集效率变化关系.
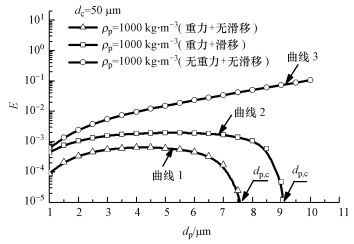 |
| 图 3 雨滴表面滑移效应及粒子重力对捕集效率影响(dc=50 μm) Fig. 3 Effects of velocity slip at raindrop surface and gravity on particles capture efficiencies for dc=50 μm |
比较图中捕集效率曲线1和2可见, 考虑雨滴表面流体滑移效应后(曲线2), 粒子的捕集效率有较明显的增加, 如在dp=1 μm时, 滑移效应导致粒子捕集效率有近1个数量级的增加; 此外, 随着粒径的增大, 有滑移和无滑移条件下, 粒子捕集均出现了临界粒径dp, c(即dp>dp, c时, 则粒子不被捕集), 但考虑滑移条件时, 临界粒径(dp, c=9 μm)明显大于无滑移情形(dp, c=7.5 μm).
为考察重力作用对粒子捕集效率的影响, 在无滑移条件(硬球模型)下给出粒子在无重力作用时的捕集效率计算结果以作为比较(图 3中曲线3), 结果表明, 忽略粒子重力作用后, dp=1 ~10 μm粒子的捕集效率明显高于有重力作用时的计算值(曲线1), 且捕集效率随粒径呈单调递增趋势, 这不同于有重力作用时的捕集效率随粒径的增加呈现先增加后减小的变化特征(曲线1和2).
据粒子动力学方程(5), 可对重力作用下粒子捕集效率随粒径增大出现下降的变化特征作出物理解析.由式(5) 可知, 在相同流场背景下, 表征粒子惯性大小的St数和表征粒子重力大小的Ga数是决定粒子轨迹的两个特征参量, 这两个参量的值均随粒子直径增加而增大, 然而重力作用方向与粒子的来流方向相反, 本质上阻止粒子向雨滴表面运动, 因此, 对粒子捕集起削弱作用.显然St数增加, 粒子的惯性捕集作用也随之增加.若粒子重力对捕集效率的削弱作用强于粒子惯性对粒子捕集的增强作用, 则粒子捕集效率将随粒径增加出现下降趋势, 如图 3中曲线1和2给出的结果.
为了直观了解雨滴表面流体滑移效应和粒子重力对粒子捕集行为的影响, 据图 3的结果, 取dp=8 μm和dp=10 μm两种代表性粒子, 分别给出了它们绕雨滴运动轨迹计算结果, 如图 4所示.由于在雨滴背风面上未观察到粒子的捕集行为, 故图 4仅给出了迎风面粒子的轨迹物理图像.
 |
| 图 4 粒子绕雨滴的运动轨迹(dc=50 μm) Fig. 4 Particle trajectories passing through a raindrop with dc=50 μm |
图 4a为dp= 8 μm粒子在有无滑移时的运动轨迹比较, 雨滴中心轴线左侧为有滑移效应时的运动轨迹(液体球模型), 右侧则为无滑移效应时的轨迹(硬球模型), 两组轨迹的起点y坐标值相同, 以保证这两种情形下粒子运动的初始条件相同.比较发现, 若考虑雨滴表面流体滑移效应时, 则dp=8 μm粒子能获得有效捕集效率值(即有粒子被捕集), 而无滑移时, 所有来流粒子均逃逸了雨滴表面而未捕集, 这与图 3的捕集效率计算结果一致.图 4b比较了dp=10 μm, ρp=1000 kg·m-3的粒子在有重力和无重力作用下绕雨滴的运动轨迹.可见, 忽略粒子的重力作用, 由不同位置点释放的粒子均被雨滴捕集; 而考虑重力作用后, 粒子在接近雨滴表面时, 因重力作用最终沿相同的轨迹绕过雨滴而未捕集.这表明重力对这一尺度粒子捕集有显著的削弱作用.
考虑到不同雨滴尺度对应不同雨滴终端下落速度U∞, 而影响粒子捕集的St数和Ga数均与U∞有关, 故考虑进一步给出了dc=100 μm雨滴对粒子捕集效率的计算结果, 如图 5所示.
 |
| 图 5 雨滴表面滑移效应及重力对粒子捕集效率影响(dc=100 μm) Fig. 5 Effects of velocity slip at raindrop surface and gravity on particles capture efficiencies for dc=100 μm |
图 5结果显示, dc=100 μm的雨滴对ρp=1000 kg·m-3的粒子在有、无滑移时的捕集效率随粒径均呈单调递增趋势(图 5中曲线1和2), 未出现图 3中的临界捕集粒径, 原因是由于雨滴尺度增大, 相应的终端下落速度U∞亦增大, 故粒子的惯性捕集作用也随之增强(即St数增大), 而粒子的重力作用则与雨滴终端下落速度U∞成反比(即Ga值降低), 从而惯性捕集作用强于重力对粒子捕集的削弱作用.
若保持雨滴尺寸不变, 增大粒子密度, 即增大粒子的重力作用(图中曲线3和4), 可观察到ρp=2000 kg·m-3时, dp=1.5~6 μm粒径段的捕集效率趋于零, 这是由于该粒径段粒子的惯性无法克服重力对粒子捕集的削弱作用; 而当dp>6 μm时, 粒子的惯性捕集作用得到了显著增强, 捕集效率随粒径的增大而迅速增加.此外, 对ρp=2000 kg·m-3粒子, 仍可观察到滑移效应对小粒子的捕集起较明显的增强效果(图中曲线3), 如滑移条件下dp=1 ~1.5 μm粒子的捕集效率大于零, 而无滑移时该粒径段粒子无法被捕集; 对于较大粒子(dp>6 μm), 雨滴表面流体滑移效应对粒子捕集的增强效果甚微.
图 6给出了几种情形下ρp=2000 kg·m-3粒子绕dc=100 μm雨滴的轨迹计算结果.所有情况下, 仍未观察到粒子在雨滴背风面出现捕集作用, 故图 6也仅给出雨滴迎风面的粒子轨迹物理图像.图 6a为dp=1 μm粒子在有无滑移作用时的粒子运动轨迹的比较.结果显示, 在滑移条件(液体球)下, 粒子仍可被捕集; 而无滑移时(硬球), 尽管粒子轨迹线已十分接近雨滴表面, 但理论上捕集仍未发生.图 6b给出的是图 5中粒子密度为ρp=2000 kg·m-3时, 临界粒径dp, c两侧附近的dp=5.5 μm和dp=6.5 μm两种直径粒子的运动轨迹, 可见dp=5.5 μm的粒均未捕集, 而dp=6.5 μm粒子, 因惯性作用强于重力的削弱作用, 可观察到有较多的粒子被捕集, 这与图 5给出的捕集效率计算结果吻合.
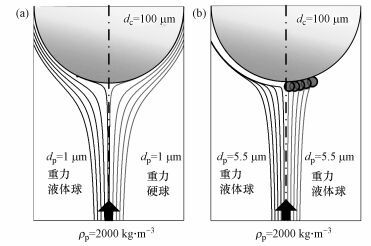 |
| 图 6 粒子绕雨滴的运动轨迹(dc=100 μm) Fig. 6 Particle trajectories passing through a raindrop with dc=100 μm |
上述讨论结果已清晰表明, 两种小尺度雨滴表面的流体滑移效应及粒子的重力作用均对粒子捕集效率产生了实质性影响, 且均与雨滴尺寸、粒子尺度及密度等多个物理量有关.根据动力学相似原理, 可进一步考虑以参量组形式给出更为简洁的捕集效率物理图像.
考察粒子动力学方程式(5) 可知, 若表征粒子惯性参量的Stokes数St和表征重力作用的Galileo数Ga相同, 则粒子的动力学方程相似.而粒子捕集条件, 即式(9) 中的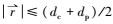
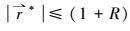
|
(13) |
式中, 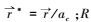
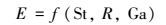
|
(14) |
考虑雨滴表面流体滑移效应为雨滴固有的动力学特性, 且已对粒子捕集产生了实质性影响, 因此, 进一步数值求解粒子的捕集效率E与St、R及Ga数的关系时, 考虑在H-R流场背景下进行, 计算结果表示在图 7中.图中Ga值表示粒子所受重力的大小, 方向与粒子运动方向相反.
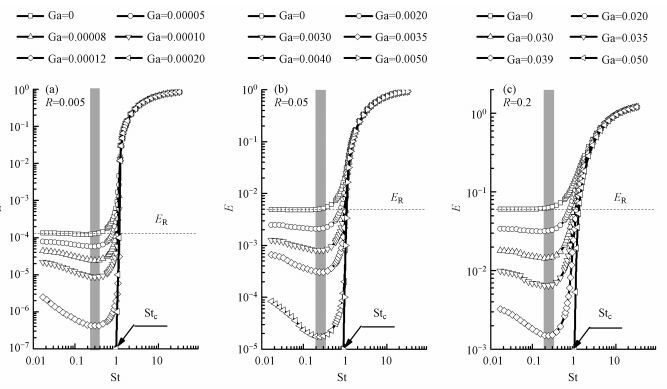 |
| 图 7 不同重力参数下粒子的惯性与拦截耦合捕集效率 Fig. 7 Combined particles capture efficiencies due to inertial impaction and interception for different values of gravity |
图 7的结果表明, 若忽略粒子受到的重力作用(Ga= 0), 即仅考虑惯性碰撞和拦截两种捕集机理的耦合作用, 则当St<0.2时, 3种拦截参数下(R=0.005、0.05和0.2) 粒子捕集效率几乎不随St数变化, 这表明惯性捕集机理对粒子捕集已无实质贡献, 拦截效应起主导作用, 此时粒子捕集效率即为纯拦截效率ER (图中虚线对应的效率值).随着St数进一步增大, 粒子惯性捕集作用显著增强, 捕集效率随St数迅速增大.
若在这两种捕集机理基础上再耦合粒子的重力作用, 则粒子的捕集效率曲线随St数的变化关系完全不同于无重力时的结果.由图 7可知, 3种拦截参数下粒子捕集效率曲线在某一St数区间均存在捕集效率“低谷”(即效率最低值, 图中灰色区域), 且Ga值越大, 最低值愈小.此外, 注意到3种拦截参数R下, 不同重力参数Ga给出的捕集效率“低谷”所对应的St数均处于0.2<St<0.3的狭窄区间.这表明重力作用对这一区间粒子捕集的削弱作用最大.
图 7的结果还显示, 3种拦截参数下, 当Ga值达到某一临界值时, 则粒子捕集效率出现与纯惯性捕集(R=0) 类似的临界St数(Stc)(Langmuir, 1948; Beard et al., 1974; Fonda et al., 1960), 即St<Stc, 则粒子不被捕集.应注意到, 考虑重力作用时的Stc数是一个与重力参数Ga相关的函数, 纯惯性时Stc数显然为Ga = 0时极限情形.
上述以St、Ga和R 3个无量纲参量给出的粒子捕集效率的计算结果, 进一步表明在估计小尺度雨滴(低Re雨滴)对大气气溶胶粒子清除效率时, 应充分考虑到粒子重力对粒子捕集的削弱作用.需要指出的, 在应用图 7中单个雨滴捕集效率结果来估计大气气溶胶清除系数及降雨过程中气溶胶粒子浓度、尺度的时空演变时, 图中无量纲参数(St、Ga和R)计算均采用粒子的空气动力学等效直径和粒子的等效密度(ρp=1000 kg·m-3).
4 结论(Conclusions)1) 低Re数下雨滴表面的流体滑移效应对气溶胶粒子的捕集起增强作用, 其增强程度与雨滴尺寸、粒子尺度及粒子密度等物理参量均有关.因此, 在估计小雨滴对气溶胶粒子降雨清除效率时, 应考虑到雨滴表面流体的滑移效应, 否则将有可能低估气溶胶粒子的降雨清除系数.
2) 在粒子惯性捕集和拦截捕集机理基础上耦合粒子的重力作用后, 计算结果表明, 由于雨滴的终端下落速度随雨滴尺寸的增大而增加, 尺寸愈小的雨滴, 重力作用对粒子捕集的削弱愈明显.
3) 不同拦截参数R下, 重力作用对于0.2<St<0.3区间粒子捕集的削弱作用最为显著.因此, 在估计该区间粒子的降雨清除系数时, 应充分考虑粒子的重力作用, 否则将可能导致这一区间粒子降雨清除效率的过高估计.
| [${referVo.labelOrder}] | Bae S Y, Jung C H, Kim Y P. 2010. Derivation and verification of an aerosol dynamics expression for the below-cloud scavenging process using the moment method[J]. Journal of Aerosol Science, 41(3): 266–280. DOI:10.1016/j.jaerosci.2009.11.006 |
| [${referVo.labelOrder}] | Bae S Y, Jung C H, Kim Y P. 2014. The influence of electric charge on minimum particle scavenging efficiency particle size during below-cloud scavenging processes[J]. Journal of Aerosol Science, 67(1): 177–187. |
| [${referVo.labelOrder}] | Baklanov A, Sørensen J H. 2001. Parameterisation of radionuclide deposition in atmospheric long-range transport modeling[J]. Physics and Chemistry of the Earth, Part B: Hydrology, Oceans and Atmosphere, 26(10): 787–799. DOI:10.1016/S1464-1909(01)00087-9 |
| [${referVo.labelOrder}] | Beard K V, Bringi V N, Thurai M. 2010. A new understanding of raindrop shape[J]. Atmospheric Research, 97(4): 396–415. DOI:10.1016/j.atmosres.2010.02.001 |
| [${referVo.labelOrder}] | Beard K V, Bringi V N, Thurai M. 2010. A new understanding of raindrop shape[J]. Atmospheric Research, 97(4): 396–415. DOI:10.1016/j.atmosres.2010.02.001 |
| [${referVo.labelOrder}] | Beard K V, Grover S N. 1974. Numerical collision efficiencies for small raindrops colliding with micron size particles[J]. Journal of the Atmospheric Sciences, 31(2): 543–550. DOI:10.1175/1520-0469(1974)031<0543:NCEFSR>2.0.CO;2 |
| [${referVo.labelOrder}] | Beizaie M, Tien C. 1980. Particle deposition on a single spherical collector a three-dimensional trajectory calculation[J]. The Canadian Journal of Chemical Engineering, 58(1): 12–24. DOI:10.1002/cjce.v58:1 |
| [${referVo.labelOrder}] | Croft B, Lohmann U, Martin R V, et al. 2009. Aerosol size-dependent below-cloud scavenging by rain and snow in the ECHAM5-HAM[J]. Atmospheric Chemistry and Physics, 9(14): 4653–4675. DOI:10.5194/acp-9-4653-2009 |
| [${referVo.labelOrder}] | Duhanyan N, Roustan Y. 2011. Below-cloud scavenging by rain of atmospheric gases and particulates[J]. Atmospheric Environment, 45(39): 7201–7217. DOI:10.1016/j.atmosenv.2011.09.002 |
| [${referVo.labelOrder}] | Fonda A, Herne H. 1960. The classical computation of the aerodynamic capture of particle by spheres[J]. Int J Air Pollut, 193(1): 26–34. |
| [${referVo.labelOrder}] | Friedlander S K. 1957. Mass and heat transfer to single spheres and cylinders at low Reynolds numbers[J]. American Institute of Chemical Engineers, 3(1): 43–48. DOI:10.1002/(ISSN)1547-5905 |
| [${referVo.labelOrder}] | Fuchs N A. 1964. The mechanics of aerosols[M]. New York: Dover Publications, Inc. |
| [${referVo.labelOrder}] | Greenfield S M. 1957. Rain scavenging of radioactive particulate matter from the atmosphere[J]. Journal of Atmospheric Sciences, 14(2): 115–125. |
| [${referVo.labelOrder}] | Grover S N, Pruppacher H R, Hamielec A E. 1977. A numerical determination of the efficiency with which spherical aerosol particles collide with spherical water drops due to inertial impaction and phoretic and electrical forces[J]. Journal of the Atmospheric Sciences, 34(10): 1655–1663. DOI:10.1175/1520-0469(1977)034<1655:ANDOTE>2.0.CO;2 |
| [${referVo.labelOrder}] | Henzing J S, Olivié D J L, Van Velthoven P F J. 2006. A parameterization of size resolved below cloud scavenging of aerosols by rain[J]. Atmospheric Chemistry and Physics, 6(11): 3363–3375. DOI:10.5194/acp-6-3363-2006 |
| [${referVo.labelOrder}] | Hinds W C. 2012. Aerosol technology: properties, behavior, and measurement of airborne particles[M]. New York: John Wiley & Sons, Inc. |
| [${referVo.labelOrder}] | 华凤皎, 刘晓燕, 亢燕铭. 2013. 雨滴表面惯性粒子捕集的湍流效应数值分析[J]. 中国环境科学, 2013, 33(9): 1585–1590. |
| [${referVo.labelOrder}] | Jung C H, Kim Y P, Lee K W. 2003. A moment model for simulating raindrop scavenging of aerosols[J]. Journal of Aerosol Science, 34(9): 1217–1233. DOI:10.1016/S0021-8502(03)00098-3 |
| [${referVo.labelOrder}] | Langmuir I. 1948. The production of rain by a chain reaction in cumulus clouds at temperatures above freezing[J]. Journal of Meteorology, 5(5): 175–192. DOI:10.1175/1520-0469(1948)005<0175:TPORBA>2.0.CO;2 |
| [${referVo.labelOrder}] | Leong K H, Beard K V, Stukel J J, et al. 1982. Factors affecting the collision of aerosol particles with small water drops[J]. Aerosol Science and Technology, 2(3): 341–349. DOI:10.1080/02786828308958639 |
| [${referVo.labelOrder}] | Levich V G. 1962. Physicochemical hydrodynamics [M]. New Jersey: Prentice-Hall |
| [${referVo.labelOrder}] | 李庆扬. 2000. 数值计算原理[M]. 北京: 清华大学出版社. |
| [${referVo.labelOrder}] | 罗淦, 王自发. 2006. 全球环境大气输送模式(GEATM)的建立及其验证[J]. 大气科学, 2006, 30(3): 504–518. |
| [${referVo.labelOrder}] | Prem A, Pilat M J. 1978. Calculated particle collection efficiencies by single droplets considering inertial impaction, Brownian diffusion and electrostatics[J]. Atmospheric Environment, 12(10): 1981–1990. DOI:10.1016/0004-6981(78)90134-8 |
| [${referVo.labelOrder}] | Quérel A, Monier M, Flossmann A I, et al. 2014. The importance of new collection efficiency values including the effect of rear capture for the below-cloud scavenging of aerosol particles[J]. Atmospheric Research, 142(6): 57–66. |
| [${referVo.labelOrder}] | Reist P C. 1993. Aerosol Science and Technology[M]. New York: McGraw-Hill Press. |
| [${referVo.labelOrder}] | Slinn W G N. 1977. Some approximations for the wet and dry removal of particles and gases from the atmosphere[J]. Water, Air and Soil Pollution, 7(4): 513–543. |
| [${referVo.labelOrder}] | Sportisse B. 2007. A review of parameterizations for modelling dry deposition and scavenging of radionuclides[J]. Atmospheric Environment, 41(13): 2683–2698. DOI:10.1016/j.atmosenv.2006.11.057 |
| [${referVo.labelOrder}] | Stulov L D, Murashkevich F I, Fuchs N. 1978. The efficiency of collision of solid aerosol particles with water surfaces[J]. Journal of Aerosol Science, 9(1): 1–6. DOI:10.1016/0021-8502(78)90057-5 |
| [${referVo.labelOrder}] | Wang A, Song Q, Yao Q. 2016. Study on inertial capture of particles by a droplet in a wide Reynolds number range[J]. Journal of Aerosol Science, 93(12): 1–15. |
| [${referVo.labelOrder}] | Wang H C, Leong K H, Stukel J J, et al. 1983. Collection of hydrophilic and hydrophobic charged submicron particles by charged water droplets[J]. Journal of Aerosol Science, 14(6): 703–712. DOI:10.1016/0021-8502(83)90053-8 |
| [${referVo.labelOrder}] | Wang P K, Grover S N, Pruppacher H R. 1978. On the effect of electric charges on the scavenging of aerosol particles by clouds and small raindrops[J]. Journal of the Atmospheric Sciences, 35(9): 1735–1743. DOI:10.1175/1520-0469(1978)035<1735:OTEOEC>2.0.CO;2 |
| [${referVo.labelOrder}] | Wang P K. 2013. Physics and dynamics of clouds and precipitation[M]. New York: Cambridge University Press. |
| [${referVo.labelOrder}] | Wang X, Zhang L, Moran M D. 2010. Uncertainty assessment of current size-resolved parameterizations for below-cloud particle scavenging by rain[J]. Atmospheric Chemistry and Physics, 10(12): 5685–5705. DOI:10.5194/acp-10-5685-2010 |
| [${referVo.labelOrder}] | Wang X, Zhang L, Moran M D. 2014. Development of a new semi-empirical parameterization for below-cloud scavenging of size-resolved aerosol particles by both rain and snow[J]. Geoscientific Model Development, 7(3): 799–819. DOI:10.5194/gmd-7-799-2014 |
| [${referVo.labelOrder}] | 王瑛, 朱彬, 康汉青, 等. 2014. 气溶胶云下清除理论及观测研究[J]. 中国科学院大学学报, 2014, 31(3): 306–313, 321. |
| [${referVo.labelOrder}] | Yates J T, Johnson J K. 2007. Molecular physical chemistry for engineers[M]. Sausalito: University Science Books Press. |
| [${referVo.labelOrder}] | Zhang L, Wang X, Moran M D, et al. 2013. Review and uncertainty assessment of size-resolved scavenging coefficient formulations for below-cloud snow scavenging of atmospheric aerosols[J]. Atmospheric Chemistry and Physics, 13(19): 10005–10025. DOI:10.5194/acp-13-10005-2013 |
| [${referVo.labelOrder}] | 赵海波, 郑楚光. 2005. 降雨过程中气溶胶湿沉降的数值模拟[J]. 环境科学学报, 2005, 25(12): 1590–1596. DOI:10.3321/j.issn:0253-2468.2005.12.004 |
 2017, Vol. 37
2017, Vol. 37