2. Tetra Tech, Inc. 10306 Eaton Place, Ste 340, Fairfax, VA 22030;
3. 云南省高原湖泊流域污染过程与管理重点实验室, 昆明 650034;
4. 南京智水环境科技有限公司, 南京 210012;
5. 环境保护部环境规划院, 北京 100012
2. Tetra Tech, Inc. 10306 Eaton Place, Ste 340, Fairfax, VA 22030;
3. Yunnan Key Laboratory of Pollution Process and Management of Plateau Lake-Watershed, Kunming 650034;
4. Nanjing Smart Water Co. Ltd, Nanjing 210012;
5. Chinese Academy for Environmental Planning, Beijing 100012
流域负荷削减是水质目标管理的关键, 但其决策一直都面临着各种不确定性的影响(刘永等, 2012; 盛虎等, 2013):不能预测未来的状态;对其现在处于A状态或B状态不能肯定;对所处状态不能准确描述(Krogh et al., 2013).在基于模型的水质管理决策问题(model based decision making)(Kwakkel et al., 2016)中, 体现为参数不确定性、模型结构不确定性、模型输入不确定性等(董磊华, 2013; 张晓玲等, 2014).传统水质管理中处理上述不确定性的方法有很多, 其特点是依赖于对不确定性的定量表达(例如概率分布)(Ben Tal et al., 2009).然而随着对于复杂自然过程、社会过程及气候变化等诸多因素研究的不断深入, 在大型、长时间尺度的水环境决策问题中, 这些传统的不确定性的研究方法正面临挑战(Milly et al., 2008).近期诸多研究将不能用概率分布信息准确刻画的不确定性或者是决策者无法达成一致的不确定性称为深度不确定性(deep uncertainty)(Bankes, 2002; Lempert, 2002; Lempert and Groves, 2010; Herman et al., 2015),并将其与概率型不确定性(probabilistic uncertainty, stochastic uncertainty)做出区分(Gao et al., 2015), 这类不确定性是以事件发生的频率或者贝叶斯的方式所定义的可能性.而深度不确定性的数学特征就是不能被概率信息准确表达.从上述定义可以看出, 深度不确定性包含了2个方面(Trutnevyte et al., 2016):① 客观不确定性, 主要是指系统本身不可预测和不能准确描述的层面;② 主观不确定性, 主要是指决策者就某一不确定性的定量化表达不能达成共识.广义上来说, 主观不确定性包含很多层面, 例如指标选取、不同指标权重, 甚至是整体决策问题公式化的形式都存在主观不确定性, 但这些不确定性的来源是不同的.对于决策问题的公式化的主观不确定性主要来源于建模者, 而指标选取及权重主要来源于最终决策者.本文主要关注来源于决策者的不确定性.同时另一方面, 当纳入足够多的指标的时候, 指标选取的不确定性会转化为不同评价指标权重的衡量上, 虽然现在存在多种赋权方法, 例如层次分析法(屈晓燕等, 2010)、模糊权重法(黄慧梅等, 2005), 但在面临过程比较复杂的决策问题时, 不管是主、客观赋权法, 方法本身的选择也存在主观性, 所以仍旧不能避免上述提到的不同决策者之间无法达成共识的问题.换言之, 上述方法在面临由于主观层面所产生的深度不确定性时都不能进行有效的决策.一般意义上, 在面临深度不确定性的决策问题时, 往往要求最终的决策是稳健的(Bankes, 2002), 即最终决策能够在足够多的合理的权重范围下保持最优性(Herman et al., 2015), 即避免单一权重的微小改动导致最优决策比较大的变化(Matrosov et al., 2013), 使最优决策不依赖于某一个具体的权重而只是依赖于权重合理范围的选取.目前已有部分研究做过类似的分析, 如陈星等(2012)采用敏感性分析方法识别稳健的决策方案, 但由于其研究中只存在5个决策变量, 并且忽视了最优决策中决策变量之间的相关性, 在面临大型的决策过程中会存在难以找到稳健决策的困境.为此, 针对水质管理中由于主观不确定性导致的赋权不确定性的问题, 本文提出一种以遍历合理权重的采样为基础、以稳健性指标(Robustness Index, RI)(Moody and Brown, 2013)为筛选标准、以遗传算法为计算引擎的决策方法, 并将其应用在八里湖流域污染负荷削减决策问题中.
2 研究对象与方法(Materials and methodology)决策问题中的备选方案个数可以是有限个也可以是无限个.由于有限个方案可以看作是无限个方案下的特殊情况, 同时流域管理问题特别是在负荷削减问题上, 方案往往是无限的, 所以后续的讨论侧重于备选方案是无限个的情况.针对主观不确定性的稳健决策方法主要分为3个计算步骤(图 1): ① 遍历采样所有合理权重, 计算每一个权重情况下的最优方案或方案集; ② 确定稳健性的计算方法; ③ 形成稳健优化问题并采用遗传算法进行求解.
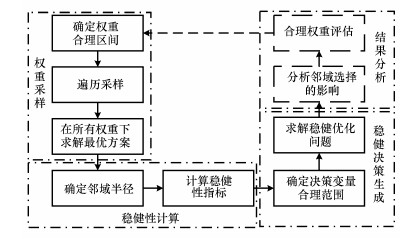 |
| 图 1 针对主观不确定性的稳健决策方法计算步骤 Fig. 1 Flowchart of finding robust decision under subjective deep uncertainty |
首先设定不同指标的权重的合理区间, 这个区间的设定可以较为宽泛, 而不必追求精确, 只需囊括所有可能的合理值, 最宽泛的情况也即所有的权重都设置在0~1之间且满足加和为1.在决策中, 每确定一组权重总能得到一个或者多个最优方案所组成的最优解集(可以用非劣解的前沿面来代替):
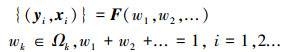
|
(1) |
式中,wk表示第k个权重, Ωk表示权重第k个分量合理的取值空间, 所有的权重加和为1. F表示一种对应关系, 即一组确定的权重对应着一个或一组最优方案, 其中向量xi表示决策变量, 向量yi表示对应决策的目标.例如在流域污染负荷削减问题中, xi为每个污染源的削减率, yi为该方案的削减总量或者削减成本.在权重合理的取值向量空间Ω采用特定的采样方法, 如随机采样或拉丁超立方抽样法(Mckay et al., 1979), 采样次数为N即有N组权重, 可以得到至少N个方案, 与取值空间Ω一起作为稳健决策的基础.
2.2 确定稳健性的计算方法衡量稳健性的指标主要分为4类(Herman et al., 2015), 其中能体现出在足够多的权重情况下保持最优性这一特征的指标为稳健性指标RI(Moody and Brown, 2013).稳健性指标有连续形式和离散形式两种, 由于权重是连续的, 所以稳健性指标应当采用连续形式.但稳健性指标是高度非线性的, 连续形式很难直接求解, 在前述已经遍历所有合理取值空间的情况下, 可采用其离散形式进行求解.
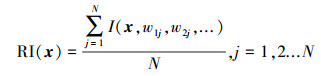
|
(2) |
式中,N为权重的遍历采样过程中的采样个数, 而I为示性函数, 取值为0或者1, 表征某一决策向量x在第j组权重取值的情况下是否具有最优性, 如果有最优性则为1, 否则为0.
计算示性函数是求解RI的关键, 即何种情况下决策x在第j组权重下具有最优性.从式(1) 得知, 每一组权重的取值都会对应一个或者多个最优方案, 对于式(2) 中的决策x与第j组权重下的最优方案完全重合几乎不可能, 但可以足够接近, 所以如果决策x与第j组权重下的最优方案中的至少一个足够接近, 就可以认为决策x在第j组权重下具有最优性.而衡量两个方案是否足够接近的最简单和直观的方法就是比较决策变量x的每一个分量是否在第j组权重的最优决策对应的每一个分量的邻域内, 如果每一个分量都在最优决策对应分量的邻域内, 就可以认为两个方案足够接近, 即:
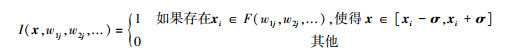
|
(3) |
式中,xi-σ及xi+σ分表表示最优决策每个分量邻域的上界和下界, σ表示邻域半径.而邻域的范围根据具体的情况, 例如备选方案每个决策变量的量纲、范围的大小及实际决策的意义事先给定, 但必须同时足够小才能保证所求出的决策满足原问题的约束要求.
2.3 稳健方案的求解方法根据2.1节中遍历合理权重取值所得到的方案及实际经验, 可以初步确定可能的稳健方案的每一个决策变量的范围,即向量空间Ω*(或直接设定为原问题的可行域), 而每一个方案的稳健性又可通过RI计算得出, 则稳健方案需要求解下述优化问题:
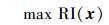
|
(4) |
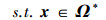
|
(5) |
通过RI的定义式可以看出, 上述优化问题是一个高度非线性的问题, 而且决策变量x所涉及到的维数很可能比较高.针对上述问题, 通常会采用进化算法进行求解(Goldberg, 1989; Maier et al., 2014).
此外, 由于上述问题高度非线性, 计算RI的过程中要对每一个权重进行最优性的评估.为了加速算法的进程、充分利用遍历采样过程中所得到的最优解的信息, 可以将第一步中得到的最优解作为遗传算法的初始种群, 提供稳健方案的“优势基因”的相关信息, 特别是关于决策变量之间相关性的信息.这一方法目前被多项研究证实可以较大程度上加速算法的收敛速度、提高算法对于最优解的逼近程度(Maier et al., 2014).
3 模型构建(Model formulation)八里湖地处江西省九江市, 湖面面积约18 km2, 流域面积约2008 km2, 含九江市3个区县共8个街道(乡镇).由于2005年左右大批工业企业的入住,八里湖湖心监测点的水质在2006—2008年间属于Ⅴ类或劣Ⅴ类水;而在2009—2013年间得益于工业及农村生活污水治理,湖心点水质基本稳定在Ⅲ类;而2014年之后由于工业企业、城市化及畜禽的综合作用,水质又有恶化的趋势.根据2014年环境保护部印发的《水质较好湖泊生态环境保护总体规划(2013—2020年)》, 八里湖近期水质目标定为Ⅱ类, 并对八里湖流域负荷削减提出了更严格的要求.
为了有效支撑八里湖的近期水质目标管理要求, 本团队在前期对八里湖进行加密监测的基础上, 采用SWAT模型构建了流域模型, 并在以三维水质水动力模型EFDC为开发内核的IWIND-LR交互平台上构建了八里湖的水质模型(南京智水环境科技有限公司等, 2016).由于八里湖的总氮(TN)近年一直处于Ⅳ~Ⅴ类, 距离Ⅱ类的目标差距较大, 除TN外, 总磷(TP)也是重要的污染因子, 考虑到在八里湖流域TN与TP的来源特征类似, 另外由于共削减现象的存在, 对于TN的研究基本能够保证TP随之达标, 因此, 本文仅以TN负荷削减为例开展研究, 主要分析TN达到近期Ⅲ类的目标.此外, 借助新近开发的流域污染负荷-水质响应的时空数值源解析技术(邹锐等, 2016)得到了相应污染源的单位削减率与水质响应的对应关系;并在分析“异参同效”不确定性的基础上, 构建了八里湖污染负荷削减决策不确定性优化模型(风险显性区间数线性优化模型, REILP(Zou et al., 2010; Liu et al., 2011)).

|
(6) |
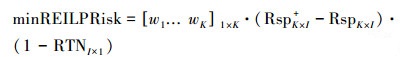
|
(7) |
使得
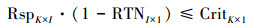
|
(8) |
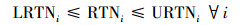
|
(9) |
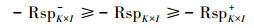
|
(10) |
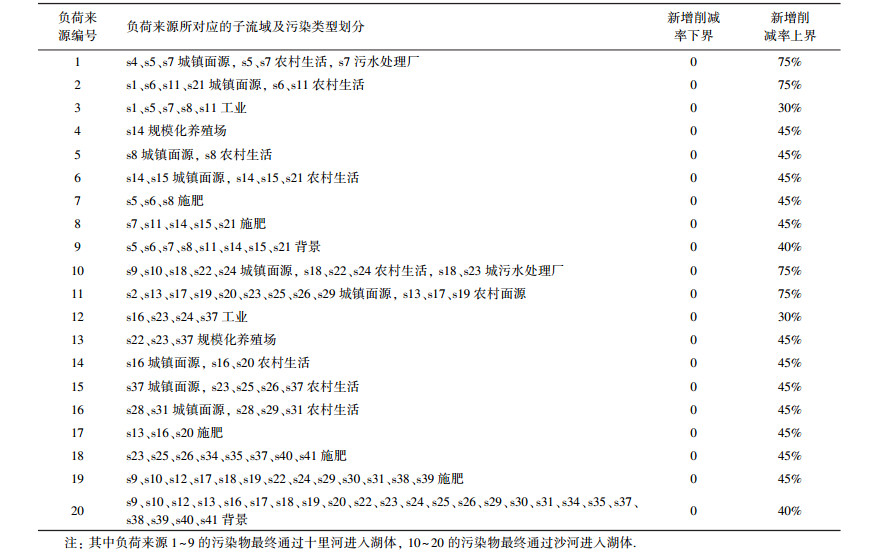
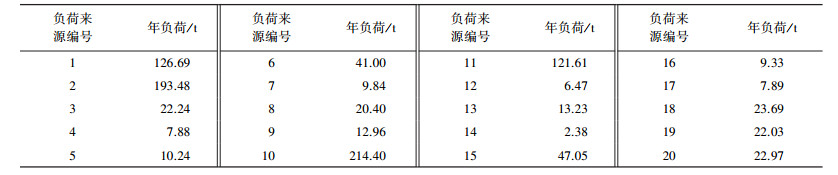
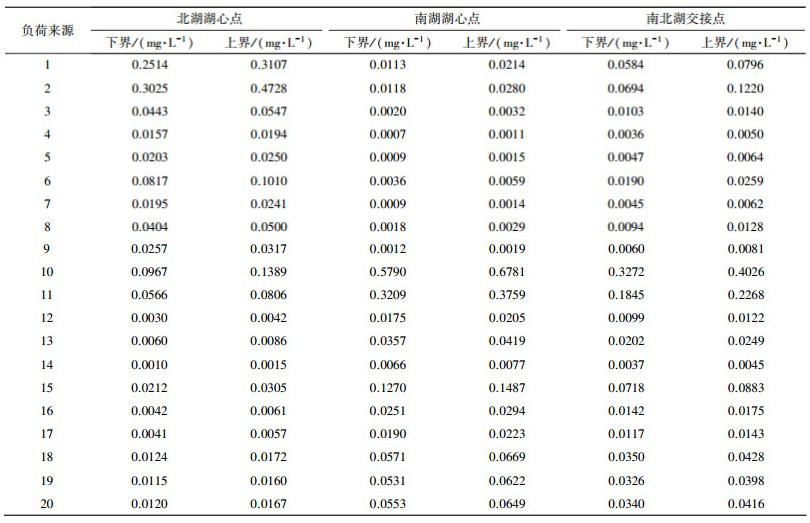
式中,RTNi表示第i个源的新增负荷削减率, 是决策变量, 其上下界分别为URTNi和LRTNi.鉴于八里湖流域完全处于九江市, 其负荷削减方案由九江市政府统筹实施, 考虑到实际问题中存在子流域边界与行政边界不匹配的问题而导致削减方案难以有效推行, 案例中负荷来源的划分按照分区和污染类型相结合的方式, 使负荷来源尽量不与区县行政边界相冲突.新增削减率上下界在前期工作中充分考虑到了技术可行性及政策要求, 新增削减率上下界的取值及负荷来源划分见表 1及图 2. Loadi表示第i个负荷来源的年负荷, 根据前期工作中SWAT模拟得出(表 2);RspK×I表示第k个站点上第i个负荷来源的负荷削减-水质响应关系, 其数值表示不削减的情况下(削减率为0) 第i个负荷来源对于第k个站点的水质贡献, 通过时空数值源解析计算得出.由于不确定性的存在, 响应关系存在上下界的波动范围, 由RspK×I+以及RspK×I-分别表示, 其值也是通过分析所有可能的参数取值, 由源解析方法得出, 取值见表 3.另外, 由于REILP方法是对原始不确定性优化模型的转化, 转化之后会使得RspK×I也转变成决策变量, 用以计算risk函数(Zou et al., 2010; Liu et al., 2011); CritK×I表示水质目标, 对于TN来说设定为1 mg·L-1; wk为权重, 在下一节中将具体解释.
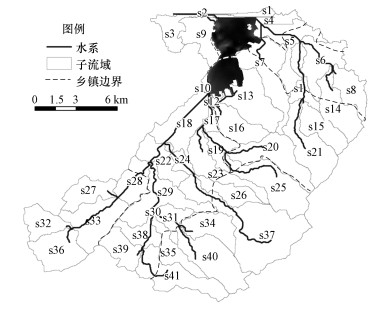 |
| 图 2 八里湖流域子流域划分示意图 Fig. 2 Sub-watershed of Lake Bali watershed |
| 表 1 八里湖各负荷来源的划分以及新增削减率的上下界 Table 1 Classification of pollution source and the high and low bounds of each source′s reduction rate |
| 表 2 八里湖流域各个负荷来源的TN年负荷 Table 2 Annual load of each source in Lake Bali watershed |
| 表 3 八里湖流域不同负荷来源对不同站点的水质贡献 Table 3 Contribution of each source at each monitoring station in Lake Bali watershed |
由前述, 参数不确定性是八里湖污染负荷削减决策中构建不确定性优化模型的原因.而由于这种不确定性的存在就会存在一定的风险, 在REILP进行不确定性模型求解的过程中就引入了risk函数来衡量这种风险.由式(7) 可知, 八里湖决策的风险是南北湖及南北湖交界3个水质监测断面的达标风险.理论上来说充分的资金投入可以使得3个监测断面都达标, 但在资金和资源有限的情况下, 作为决策者的九江市地方政府需要权衡3个断面的达标风险.对于地方政府而言, 其关心的并非湖体整体水质的达标, 而是监测断面的达标.在存在不达标的情况下, 对于不同类别的监测断面就会存在权衡关系, 而权重wk所衡量的正是决策者对于达标断面的选择偏好.上述模型的最优解是依赖于权重的.一般而言在一定范围内, 决策者希望最终的决策对于权重是不敏感的, 也就是说在足够多的权重的情况下都能保证最优性.因为对于权重的准确衡量是不可能的, 即使在某一组权重的情况下求出最优决策, 但这个决策可能在权重微小改动下对应的risk函数或削减量会显著提高(即偏离权重变动之后的最优解), 这就是需要寻找对权重wk稳健的决策的理由.
4 结果与讨论(Results and discussion) 4.1 主观深度不确定性对方案选择的影响式(6)~(10) 是典型的多目标优化问题, 同时由于risk函数的存在, 该问题也是非线性的, 一组权重对应一个多目标优化问题的非劣解集.此时, 讨论某一削减水平下的最稳健的决策才是有意义的.将权重的合理取值范围确定为0~1之间, 由于只涉及到3个权重并且只有2个自由变量, 采用拉丁超立方抽样方法抽取1000组权重.对于每一组权重, 求解式(6)~(10) 所代表的非线性多目标优化问题, 采用NSGA-Ⅱ算法(Deb et al., 2002), 得到1000个非劣解集, 每个非劣解集有21个决策方案(方案的个数取决于NSGA-Ⅱ的算法设置).求解出的所有的备选决策的年负荷削减量为143~327 t.考虑对削减水平划分之后备选决策的个数, 将削减水平分为10类, 其中后续的稳健决策将只考虑277~297 t的削减水平, 作为稳健决策的示例.这一水平内共有2100个决策, 上述采样的1000组权重都对应有一个或者多个该权重下的最优决策.
由图 3可知, 由于权重的不同所得到的方案, 即每一个负荷来源的新增削减率有很大的差别.除去图中部分来源的削减比例比较集中, 例如编号2(十里河的部分面源)新增削减比例稳定较低, 而其他负荷来源的削减比例变动范围都比较大, 并且权重的微小变化能引起最优决策显著的变动.例如考虑相似的权重(0.056, 0.806, 0.138)、(0.056, 0.891, 0.052), 都表示非常侧重第2个监测站点(南湖湖心点)的水质达标情况.但在相同的risk函数水平下, 第1个负荷来源的最优削减比例却分别为0.69和0.56, 相差较大.上述结果表明, 来源于主观层面的深度不确定性, 也即对达标站点优先性的考虑会影响最终最优决策的生成.
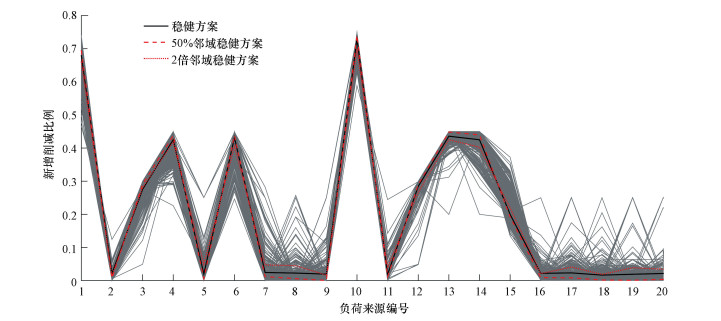 |
| 图 3 在277~297 t年负荷削减水平下的备选方案以及稳健决策 Fig. 3 Alternative decisions and robust decision with annual reduction 277~297 t |
按照在2.2~2.3节中提到的稳健方案的求解方法, 将邻域的半径设定为2.5%, 在TN的277~297 t年负荷削减水平下进行求解, 得到的稳健决策如图 3中的黑色实线所示(RI值为0.403).在1000组权重中, 该方案能够在403组权重下保持最优性, 同时经检验满足水质约束.易知, 为使得水质达标, 稳健决策在部分负荷来源的削减率上达到了上界或者下界.这是由单位污染物的削减可带来的水质改善决定的, 也就是说是由REILP模型的构建及所考虑的不确定性决定的.虽然编号2的源(十里河的部分子流域的面源)负荷很大, 但其单位负荷削减对于水质的改善程度很低, 加之在REILP计算过程中, 由于其不确定性很大导致risk函数较大, 所以在决策中的削减比例较低.但对于稳健决策而言并不是所有的都达到上界或者下界, 比如编号1的源(十里河的部分面源)及编号15(沙河的部分面源).说明所求出的稳健决策, 不仅考虑了负荷所能带来的水质改善, 还考虑了在各个站点之间的所有可能的权衡.由于案例中将合理权重范围设置成0~1, 稳健性决策寻找的就是,当不管如何考虑监测站点的平衡时, 备选决策最集中的结构, 也就是最稳健的方案.
当然在求解稳健方案的时候, 邻域的设定影响了对这种稳健结构的求解.为了验证稳健方案是否随着邻域选择而改变, 将邻域半径缩小为原来的一半(1.25%, 所求得RI值为0.117) 及扩大为原来2倍(5%, 所求得RI值为0.835) 进行同样的求解, 得到的稳健决策如图 3所示.可以看出, 在达到上下界的负荷来源削减比例上, 3个决策有明显差别.这是由邻域计算稳健方案的必然结果, 因为要想使得RI更大, 达到削减上界或者达到下界的最稳健决策应距离上界或者下界刚好为邻域的半径的距离, 这恰好说明了稳健决策的计算是有效的.从图 3可知, 为了保证水质达标, 主要依靠点源的控制, 绝大部分的面源新增削减比例都比较小.这是因为不管参数的不确定性为何, 这些点源及部分面源(削减比例达到上限的负荷来源)对于监测站点的水质影响都是显著的.这和美国实行TMDL过程中对点源优先控制和规划, 而对不确定性较大的面源作为保障性措施的经验是吻合的(杨龙等, 2008).
4.3 稳健方案所对应的权重情况求出稳健方案之后, 还需要看这些稳健方案所对应的权重情况(Deitrick, 2013), 也即使得式(3) 为1的权重(图 4).从图 4可知, 一个稳健决策所对应的能够维持其最优性的权重情况是不连续的, 几乎涵盖了整个合理的取值范围.这说明从权重到最优方案是一个非线性的关系.由式(7) 可以看出, 可以去掉权重直接将其拆分成3个目标, 则原优化问题变为了4个目标的优化问题, 可以避免权重的不确定性.但这样做相比于现在的处理方式有3点缺陷:① 由于决策变量的维度比较高, 加之目标较多, 现有的智能算法很难保证能够得到多目标的前沿面(Reed et al., 2013); ② 即使求解出多目标的前沿面, 在八里湖的案例中由于考虑了自然过程的不确定性(REILP部分)及决策不确定性(稳健决策部分), 高维的前沿面很难区分这两者之间的关系; ③ 由于决策中的权重是有实际意义的, 结合图 4所示的权重分布, 可以更好地结合经验判断(Deitrick, 2013), 从而做出权衡以及对合理权重进一步调整.
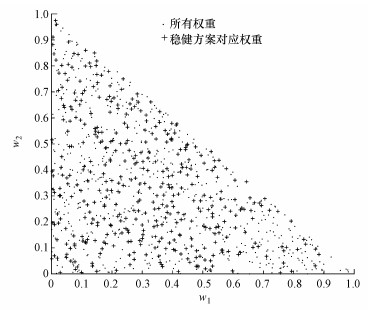 |
| 图 4 稳健决策所对应的权重情况 Fig. 4 The corresponding weights which contribute the robustness of robust decision |
1) 由于主观深度不确定性的存在, 用权重定量化主观不确定性的微小变动可能会引起最优决策比较大的改变, 从而使得单一权重所确定的最优决策失去意义.
2) 以稳健性指标最大化为目标结合对进化算法的特殊初始条件的设定, 能够识别出来稳定决策, 在八里湖案例中, 经过邻域半径变动的检验之后得出, 稳健削减方案是以点源及部分特定面源的控制为基本结构.
3) 虽然权重到对应的最优决策是非线性的, 八里湖稳健决策在考虑削减比例上下波动5%的范围内, 能够覆盖83.5%的情况, 说明该决策能够满足绝大部分情况下对于不同站点之间的权衡考虑, 可以为最终决策提供有效支持.
| [${referVo.labelOrder}] | Bankes S C. 2002. Tools and techniques for developing policies for complex and uncertain systems[J]. Proceedings of the National Academy of Sciences, 99 Suppl 3(Supplement 3): 7263–7266. |
| [${referVo.labelOrder}] | Ben-Tal A, Ghaoui L E, Nemirovski A. 2009. Robust Optimization[M]. Princeton: Princeton University Press: ⅸ–xxii. |
| [${referVo.labelOrder}] | 陈星, 邹锐, 刘永, 等. 2012. 风险显性区间数线性规划模型(REILP)解对约束风险偏好的敏感性与稳健性研究[J]. 北京大学学报:自然科学版, 2012, 48(6): 942–948. |
| [${referVo.labelOrder}] | Deb K, Pratap A, Agarwal S, et al. 2002. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 6(2): 182–197. DOI:10.1109/4235.996017 |
| [${referVo.labelOrder}] | Deitrick S. 2013. Implicit Visualization as Usable Science Visualizing Uncertainty as Decision Outcomes[D]. Phoenix: Arizona State University https://repository.asu.edu/attachments/110230/content/Deitrick_asu_0010E_12598.pdf |
| [${referVo.labelOrder}] | 董磊华. 2013. 考虑气候模式影响的径流模拟不确定性分析[D]. 武汉: 武汉大学. 17-21 |
| [${referVo.labelOrder}] | Gao L, Bryan B A, Nolan M, et al. 2015. Robust global sensitivity analysis under deep uncertainty via scenario analysis[J]. Environmental Modelling & Software, 76(C): 154–166. |
| [${referVo.labelOrder}] | Goldberg D E. 1989. Genetic algorithms in search, optimization, and machine learning[M]. Boston: Addison-Wesley Pub. Co.. |
| [${referVo.labelOrder}] | Herman J D, Reed P M, Zeff H B, et al. 2015. How should robustness be defined for water systems planning under change?[J]. Journal of Water Resources Planning & Management, 141(10): 04015012. |
| [${referVo.labelOrder}] | 黄慧梅, 金菊良, 汪淑娟. 2005. 改进的模糊层次分析法在水污染控制方案优选中的应用[J]. 农业系统科学与综合研究, 2005, 21(1): 55–57. |
| [${referVo.labelOrder}] | Krogh G V, Takeuchi H, Kase K, et al. 2013. Towards organizational knowledge[M]. London: Palgrave Macmillan UK.: 306–349. |
| [${referVo.labelOrder}] | Kwakkel J H, Haasnoot M, Walker W E. 2016. Comparing robust decision-making and dynamic adaptive policy pathways for model-based decision support under deep uncertainty[J]. Environmental Modelling & Software, 86: 168–183. |
| [${referVo.labelOrder}] | Lempert R J. 2002. A new decision sciences for complex systems[J]. Proceedings of the National Academy of Sciences, 99(suppl 3): 7309–7313. |
| [${referVo.labelOrder}] | Lempert R J, Groves D G. 2010. Identifying and evaluating robust adaptive policy responses to climate change for water management agencies in the American west[J]. Technological Forecasting & Social Change, 77(6): 960–974. |
| [${referVo.labelOrder}] | Liu Y, Zou R, Guo H C. 2011. A risk explicit interval linear programming model for uncertainty-based nutrient-reduction optimization for the lake qionghai watershed[J]. Journal of Water Resources Planning and Management-ASCE, 137(1): 83–91. DOI:10.1061/(ASCE)WR.1943-5452.0000099 |
| [${referVo.labelOrder}] | 刘永, 邹锐, 郭怀成, 等. 2012. 智能流域管理研究[M]. 北京: 科学出版社: 193–243. |
| [${referVo.labelOrder}] | Maier H R, Kapelan Z, Kasprzyk J, et al. 2014. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions[J]. Environmental Modelling & Software, 62: 271–299. |
| [${referVo.labelOrder}] | Matrosov E S, Woods A M, Harou J J. 2013. Robust decision making and info-gap decision theory for water resource system planning[J]. Journal of Hydrology, 494(7): 43–58. |
| [${referVo.labelOrder}] | Mckay M D, Beckman R J, Conover W J. 1979. A comparison of three methods for selecting values of input variables in the analysis of output from a computer[J]. Technometrics, 21(1): 239–245. |
| [${referVo.labelOrder}] | Milly P C, Betancourt J, Falkenmark M, et al. 2008. Climate change. Stationarity is dead: whither water management?[J]. Science, 319(5863): 573–574. DOI:10.1126/science.1151915 |
| [${referVo.labelOrder}] | Moody P, Brown C. 2013. Robustness indicators for evaluation under climate change: Application to the upper Great Lakes[J]. Water Resources Research, 49(49): 3576–3588. |
| [${referVo.labelOrder}] | 南京智水环境科技有限公司, 环境保护部环境规划院, 北京大学. 2016. 九江市八里湖生态环境保护规划——八里湖流域容量总量污染控制研究[R]. 南京: 南京智水环境科技有限公司 |
| [${referVo.labelOrder}] | 屈晓燕, 张裕芬, 冯银厂, 等. 2010. 天津市PM10污染控制决策模型[J]. 环境科学研究, 2010, 23(4): 401–406. |
| [${referVo.labelOrder}] | Reed P M, Hadka D, Herman J D, et al. 2013. Evolutionary multiobjective optimization in water resources: The past, present, and future[J]. Advances in Water Resources, 51(1): 438–456. |
| [${referVo.labelOrder}] | 盛虎, 向男, 郭怀成, 等. 2013. 流域水质管理优化决策模型研究[J]. 环境科学学报, 2013, 33(1): 1–8. DOI:10.11654/jaes.2013.01.001 |
| [${referVo.labelOrder}] | Trutnevyte E, Guivarch C, Lempert R, et al. 2016. Reinvigorating the scenario technique to expand uncertainty consideration[J]. Climatic Change, 135(3/4): 1–7. |
| [${referVo.labelOrder}] | 杨龙, 王晓燕, 孟庆义. 2008. 美国TMDL计划的研究现状及其发展趋势[J]. 环境科学与技术, 2008, 31(9): 72–76. |
| [${referVo.labelOrder}] | 张晓玲, 梁中耀, 刘永, 等. 2014. 流域水质目标管理的风险识别与对策研究[J]. 环境科学学报, 2014, 34(10): 2660–2667. |
| [${referVo.labelOrder}] | Zou R, Liu Y, Liu L, et al. 2010. REILP approach for uncertainty-based decision making in civil engineering[J]. Journal of Computing in Civil Engineering, 24(4): 357–364. DOI:10.1061/(ASCE)CP.1943-5487.0000037 |
| [${referVo.labelOrder}] | 邹锐, 苏晗, 陈岩, 等. 2016. 流域污染负荷-水质响应的时空数值源解析方法研究[J]. 中国环境科学, 2016, 36(12): 3639–3649. DOI:10.3969/j.issn.1000-6923.2016.12.015 |
 2017, Vol. 37
2017, Vol. 37