2. 北京市南水北调大宁管理处, 北京 102442;
3. 贵州松柏山水库管理处, 贵阳 550025;
4. 河南省水利勘测设计研究有限公司, 郑州 450016;
5. 北京市水科学技术研究院, 北京 100048
2. Daning Management Office of the Beijing South to North Water Diversion, Beijing 102442;
3. Guizhou Songbaishan Reservoir Administrative Office, Guiyang 550025;
4. Henan Water and Power Engineering Consulting Corporation Limited, Zhengzhou 450016;
5. Beijing Water Science and Technology Institute, Beijing 100048
目前, 国家为推进生态文明建设, 在水污染治理与水生态修复方面加大了支持力度, 各地相关领域的水环境治理项目大量涌现.水生态修复工程的主要目的之一, 就是提升区域的水环境容量, 或者说提高水域的自净能力(姜霞等, 2014), 若单纯考虑前期景观效果, 没有进行水量与水质的定量分析与后期强化管理, 则很可能无法达到预期目标(秦伯强等, 2002).因此, 针对水生态修复工程的布局及对应的水体运行方案, 进行专门的定量研究是十分重要的(徐斌等, 2017).在水生态修复工程中, 除了采取增加水域面积、提高水体置换率的措施以外(王冼民等, 2017), 普遍采用了各种水质修复措施, 对生态修复工程的后期维护产生重要影响.例如, 为提升现有水域自净能力, 在湖区周边建设人工湿地(黄国动等, 2017), 通过循环吸附作用, 实现湖区水体的部分净化;从提升水景观与改善水质的角度出发, 园林规划部门通常在水域内种植浮水植物、挺水植物(吕家展等, 2017;张惠等, 2017;管永等, 2014), 在生长季节可以吸附水体中污染物, 提升水域自净能力(郝明旭等, 2017), 当然, 其死亡腐烂分解又会污染水体, 因此需要及时清理(唐金艳等, 2013;戚美侠等, 2017);随着科学技术的发展, 还出现了人工曝气、纳米吸附膜、沸石床面、物理化学试剂等各种水体净化措施(刘晓伟等, 2011;王蓉等, 2016;马荣萱等, 2006;吴鹏等, 2017;陈方明等, 2007).上述措施的共同特点是, 污染物在经过上述边界时, 被部分吸附或者吸收, 从而改善水域自净能力.另外, 有些水质修复措施在改变水域自净能力的同时, 也会改变水域流场条件, 例如水生植物的种植, 使得河道局部糙率增加, 紊动扩散系数减小, 容易形成滞留区或死水区(郑爽等, 2017;李志杰等, 2017), 对于湖区水体整体置换效率产生影响.针对上述问题, 本文通过建立二维水流-水质数学模型, 定量分析水域内生态修复措施对水流流场与污染物降解规律的影响, 为今后的实际工程应用建立了基础.
2 数学模型的基本理论(Basic theory of the mathematical model) 2.1 控制方程本文数学模型中, 采用了二维水深平均的水流控制方程:
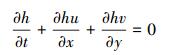
|
(1) |

|
(2) |
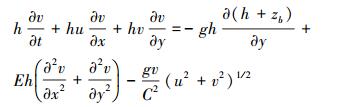
|
(3) |
相应地, 污染物输运降解控制方程为:
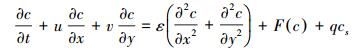
|
(4) |
式中, u、v为流速(m·s-1);h和zb为水深和床面高程(m);E为水流涡粘系数(m2·s-1);C为谢才系数, C=n-1h1/6, n为糙率;c为污染物浓度(mg·L-1);ε为污染物扩散系数(m2·s-1);q为点源流量(s-1);cs为源汇浓度(mg·L-1).F(c)为污染物降解项, 常采用一阶反应动力学模式加以描述:F(c)=-kc, k为污染物降解系数(d-1).
在污染物输运方程中, 水生态修复措施对污染物浓度分布的影响主要体现在污染物降解项上, 其中降解系数k的取值与生态修复措施的吸附特性、污染物初始浓度、空间位置等多种因素有关, 需要根据实际情况分析确定(郭儒等, 2008).对此, 采用了有限元法来离散基本控制方程, 针对不同区域分别指定不同的浓度降解系数, 并且也可通过代码修改, 采用特定的污染物降解函数.在水域中流场与吸附性边界的作用下, 污染物浓度在空间上是沿程衰减的, 同时在水域中任一点, 污染物浓度随时间增加, 然后逐渐趋于平衡值.对此, 通过采用一种特征有限元方法, 保证在强对流条件与吸附性边界作用下, 污染物浓度变化的保单调性.
2.2 特征有限元方法对于对流占优的污染物输运问题, 流场中任一点的污染物浓度变化除了当地浓度扩散外, 主要与其上游的浓度输运有关, 传统的有限元方法相当于中心差分, 需要增大耗散系数, 抹平浓度分布, 否则容易产生数值振荡.因此, 本文采用了一种特征有限元方法, 该方法只需沿着特征线找到特征点, 就可以对输运方程进行简化.具体方法如下:
在污染物输运扩散方程中, 时间导数项和对流项组成的全导数算子可用下面的隐格式代替:
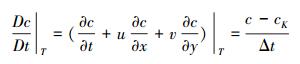
|
(5) |
式中, cK为特征浓度, 为T-Δt时刻的特征点K处的浓度值, 其位置坐标可表示为

|
(6) |
这样浓度输运方程作如下离散

|
(7) |
将式(5)代入式(7), 经整理得到每个单元内有限元离散方程
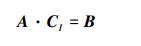
|
(8) |
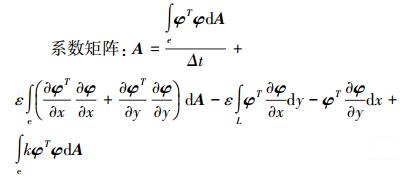
|
(9) |
右端向量:
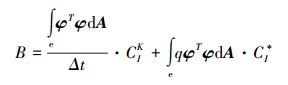
|
(10) |
式中, 单元插值形函数与加权函数相同, 均为φ=[ε, η, ζ];单元节点浓度CI=[c1, c2, c3];单元节点特征浓度CIK=[c1K, c2K, c3K];单元节点的源汇浓度CI*=[c1*, c2*, c3*].这样, 对每一个单元e求出单元系数矩阵A和右端向量B, 然后将其合成总体矩阵, 即可求得Tn时刻的节点浓度CI.
2.3 特征点的确定对于每个单元节点而言, 需通过求解式(6)中积分, 得到特征点K的位置坐标.具体方法如图 1所示, 从节点坐标开始, 沿流线向上游查找, 考虑到流线弯曲引起计算误差, 采用2阶龙格-库塔法求解:
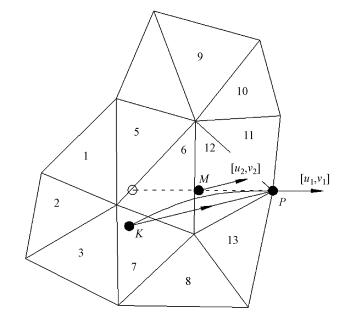 |
| 图 1 特征点坐标的求解方法 Fig. 1 Solution of characteristic point position |

|
(11) |
式中, xK、yK为浓度特征点K的位置坐标, xt、yt为节点坐标.u1、v1为节点流速, u2、v2为半程特征点M的流速.采用该方法求解上一时刻的特征点, 可将特征浓度的求解精度提高一阶.
在求得浓度特征点K的位置坐标后, 需找到其所在单元, 然后根据上一时刻的节点浓度值和形函数, 插值求解对应的浓度值CIK.为判别K点是否落在某单元内, 需求解坐标点在该单元内的三个形函数值, 若三者之和为1, 则K点位于该单元内, 若三者之和大于1, 则表明K点位于该单元之外.在程序设计中, 当首个时间步长完成后, 将存储每个节点的特征点K所在的单元号, 在下次步长开始时, 将首先从预先存储的单元编号开始查找, 当K点不在此单元内时, 则按照该单元编号上下顺位双向查找, 以提高运算速度.对于恒定问题而言, 特征点的查找只需进行1次.
3 模型检验与分析(Model verification and analysis)以滦河干流上游承德县河段为例, 该河段存在的主要污染问题为氨氮超标, 对于下游潘家口水库水质造成不利影响.研究河段如图 2所示, 其中滦河干流长度约4.7 km, 河宽平均300 m;支流老牛河在2.2 km处汇入, 河道长度约1.6 km, 河宽约200 m.本文计算中, 取该河段夏季6—9月平均流量, 其中上游入流边界1流量取30 m3·s-1, 入流边界2流量取5 m3·s-1, 出流边界流量35 m3·s-1.根据2007—2011年滦河干流各水文站实测资料分析, 滦河干流各站流量与氨氮指标之间均具有明显相关性(郭丽峰等, 2014), 按照上述规律, 入流边界1的氨氮浓度为4.2 mg·L-1, 支流入流边界2的氨氮浓度1.0 mg·L-1, 下游出流边界的氨氮浓度应为3.5 mg·L-1.上述水流与污染物浓度边界条件保持恒定.
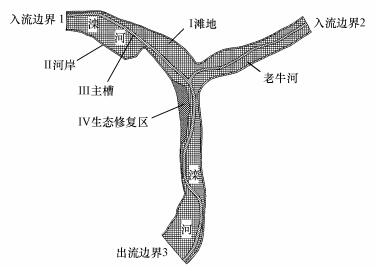 |
| 图 2 计算河段分区图 Fig. 2 Partitions of computing grid in the river regulation area |
模型计算参数中, 污染物扩散系数为水流紊动扩散系数的0.8~1.0倍, 本文取1.0倍;水流紊动扩散系数E通过采用Peclet数调节, P=ρudx/E, 一般取值10~40, 本文取20.另外, 计算河段内包含滩地Ⅰ、河岸Ⅱ、主槽Ⅲ、生态修复区Ⅳ等4种区域, 需根据实际情况给定不同的糙率系数.由于污染物扩散过程为一非恒定过程, 通过对河道流场进行分析, 上游污染物自入流边界1到达下游出流边界3历时约18 h, 本文计算历时取24 h.
研究方案分为2组, 方案1是针对现状河道污染物沿程分布规律进行验证分析, 河道内滩地糙率取0.035, 主槽糙率0.025, 河岸糙率0.04 (张秉文等, 2012), 暂不考虑水生态修复措施, 整个河段的氨氮降解系数取0.10 d-1.方案2是在区域Ⅳ内采取表面流人工湿地技术, 总面积约113316 m2.根据吴海明等(2011)的研究, 该技术在春夏季节氨氮衰减系数可达0.3 d-1, 由于该区域内密植鸢尾、水葱、香蒲、芦苇等水生植物, 糙率可取0.08.通过数学模型方法, 定量分析其大规模应用的实际效果.上述方案的模型计算参数如表 1所示.
| 表 1 河道整治工程方案模型计算参数 Table 1 Calculation parameters of river regulation project |
图 3为现状河道条件下, 河道内流场结构与污染物浓度分布的变化, 可知在滦河干流与老牛河支流汇合口下游, 形成了高流速区, 流速量级约0.12 m·s-1, 且位于河道中部.由于老牛河污染物浓度较低, 汇合口下游河道内, 污染物浓度横向分布差异较大, 污染物主要位于河道右侧, 而左侧河道水质相对较好, 至下游出流边界3附近, 断面污染物峰值可达3.3~3.6 mg·L-1, 计算值与实测资料分析结果相一致.图 4为区域Ⅳ实施表面流人工湿地工程后, 河道内流场与污染物浓度分布的变化, 可知在右岸生态修复区域, 由于水生植物密植, 使得局部糙率增大, 高流速区偏向左岸一侧, 干流污染物与支流掺混增加.同时, 生态修复区Ⅳ内降解系数增大, 使得下游污染物浓度发生改变, 至下游出流边界3附近, 污染物峰值下降至2.2~2.4 mg·L-1, 较之原状河道下降1.0 mg·L-1.上述研究表明, 通过在河道滩地内采用表面流人工湿地技术, 可明显改善水质, 本文模型对于复杂边界下的流场与污染物分布规律具有较好的模拟能力和适应性.
 |
| 图 3 现状河道流场分布情况(a)污染物浓度分布情况(b) Fig. 3 Flow field (a) and Pollutant concentration (b) distribution in the original river |
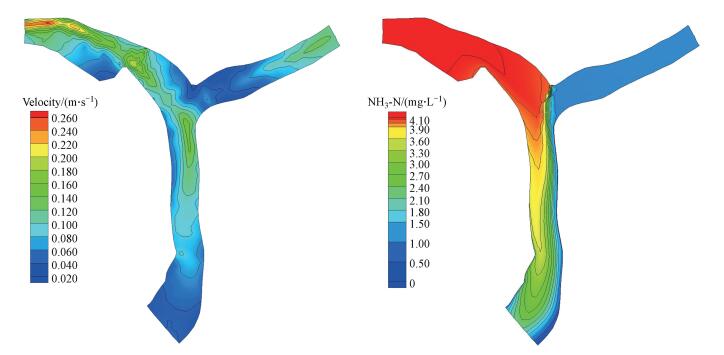 |
| 图 4 区域Ⅳ实施生态修复后, 河道流场分布图(a)及污染物浓度分布情况(b) Fig. 4 Flow field(a) and pollutant concentration(b) distribution after the ecological restoration at region Ⅳ in the river |
本文模型在求解特征点的过程中, 会遇到几种特殊的情况:首先, 当节点位于侧壁边界上时, 认为水流始终沿边界流动, 因此其特征点也应当位于边界上, 此时可按照路径长度相等的原则, 沿边界查找.第二, 当节点位于第一类边界(入流边界)上时, 入流边界上污染物特征浓度可直接取上一时刻浓度值, 鉴于入流边界上污染物浓度的法向梯度常常未知, 该方法不失为一种解决办法.第三, 当节点位于计算域内部时, 在时间步长较大、网格尺度较小时, 其特征点也可能位于边界之外, 此时又分为2种情况, 一种是特征线穿过第一类边界(入流边界), 可取其特征线与入流边界交点作为浓度特征点;另一种是特征线穿过第二类边界(侧岸边界), 此时应从其特征线与边界的交点开始, 按照剩余路径长度, 沿边界查找.由于特征点的位置基本沿着流线进行查找, 特征点位于边界以外的情况甚少出现, 计算精度可以满足实际工程需求.当流场变化剧烈或者时间步长较大时, 可采用4阶龙格库塔法以提高计算精度, 但计算量明显增加.
由于总体矩阵为高阶稀疏方阵, 存储起来将消耗大量的内存, 为此需要采用带宽存储的方法.由于采用了特征有限元法, 系数矩阵不再对称, 因此必须采用全带宽存储.同时, 由于求解过程中, 总体系数矩阵保持不变, 本文采用LU分解法, 其计算速度较高斯消元法要快.为进一步适应大尺度问题的计算, 还可将式(8)转换为隐式迭代方程, 采用多重指针数组, 实现方程系数矩阵的高效存储.另外, 在采用隐格式后, 水流计算模块的时间步长可以取得较大, 但对于浓度计算模块, 为了保证特征浓度的计算精度, 又要求较小的步长.对此, 本文模型对于水流和污染物的计算, 分别采用不同的时间步长, 在一个较长的水流计算步长T内, 进行N次污染物扩散计算, 每次污染物计算的步长为T/N, 期间水流条件保持不变.
当水位变幅较大时, 水位涨落会引起水下地形的干湿变化.为此, 当单元内水深降至某一临界值时, 将单元的属性值修改为干单元, 在下一个时间步长内, 先通过调用各单元的材料属性值来判别该单元是否加入计算, 同时确定新的边界, 这样保证了水流与污染物计算变化的同步.
当计算域中同时包含多种吸附性边界时, 需设置不同的单元属性加以区别, 分别采用不同的降解系数k与糙率系数n.当吸附性边界具有二级反应特性时, 需对式(9)中右端第四项中积分函数进行修改, 重新修改代码, 生成计算模型.
本文数学模型的计算精度取决于生态修复方案的参数取值.在实际工程应用中, 需针对所采用的具体修复措施, 通过小试或中试, 研究其在各种动水条件下对应的污染物降解系数, 然后通过本文模型定量分析其大规模应用于目标水体的实际效果.
5 结论(Conclusions)目前在许多河道环境整治工程中, 采用了许多具有吸附或吸收特性的生态修复措施, 改变了现有河道的污染物降解特性, 也引起水环境容量的变化.本文针对吸附性边界对水域污染物浓度分布的影响, 建立了平面二维水流-水质计算模型.该模型通过采用特征有限元方法, 在各种降解条件下的对流流场中均能保持污染物浓度变化的时间单调性;通过采用2阶龙格库塔法沿流线追踪上游特征点的位置, 在流线弯曲情况下, 污染物浓度的计算精度明显提高;通过在每个单元内指定水流糙率系数与污染物降解系数, 可用于评估水域中各种水质净化措施的实际效果;通过典型算例, 证明该模型具有较好的适应性和可靠性.在实际工程应用中, 可定量分析各种生态修复措施对水域净化能力的影响, 可为大规模应用方案提供决策依据.
陈方明, 陆琦. 2007. 方沸石水质净化剂的制备及其除氟研究[J]. 环境工程学报, 2007, 1(9): 30–34.
DOI:10.3969/j.issn.1673-9108.2007.09.007 |
管永, 冯智, 张聪, 等. 2014. 水生植物在河道生态修复工程中应用研究[J]. 环境科学与管理, 2014, 39(5): 149–151.
DOI:10.3969/j.issn.1673-1212.2014.05.044 |
郭丽峰, 郭勇, 罗阳, 等. 2014. 季节性Kendall检验法在滦河干流水质分析中的应用[J]. 水资源保护, 2014, 30(5): 60–67.
|
郭儒, 李宇斌, 富国. 2008. 河流中污染物衰减系数影响因素分析[J]. 气象与环境学报, 2008, 24(1): 56–59.
DOI:10.3969/j.issn.1673-503X.2008.01.014 |
郝明旭, 霍莉莉, 吴珊珊. 2017. 人工湿地植物水体净化效能研究进展[J]. 环境工程, 2017, 35(8): 5–10.
|
黄国动, 杜建强, 张瑛, 等. 2017. 基于人工湿地的水环境治理和优化技术在太湖流域的应用[J]. 湿地科学与管理, 2017, 13(3): 10–15.
DOI:10.3969/j.issn.1673-3290.2017.03.02 |
姜霞, 王书航, 杨小飞, 等. 2014. 蠡湖水环境综合整治工程实施前后水质及水生态差异[J]. 环境科学研究, 2014, 27(6): 595–601.
|
李志杰, 王丹, 朱明明, 等. 2017. 植被群河道水流特性试验研究[J]. 四川大学学报(工程科学版), 2017, 49(2): 86–91.
|
刘晓伟, 谢丹平, 李开明, 等. 2011. 曝气复氧对底泥氮素生物地球化学循环影响的作用机制研究[J]. 生态环境学报, 2011, 20(11): 1713–1719.
DOI:10.3969/j.issn.1674-5906.2011.11.022 |
吕家展, 张顺涛, 李葱碧, 等. 2017. 生态浮岛种植水生植物水质改善效果评价[J]. 环境科学与技术, 2017, 40(S1): 191–195.
|
马荣萱, 李继忠. 2006. 纳米技术及材料在环境保护中的应用[J]. 环境科学与技术, 2006, 29(7): 112–114.
DOI:10.3969/j.issn.1003-6504.2006.07.045 |
戚美侠, 王红萍, 陈杰. 2017. 冬、春季芦苇(Phragmites australis)和狭叶香蒲(Typha angustifolia)的腐解过程及其对水质的影响[J]. 湖泊科学, 2017, 29(2): 420–429.
|
秦伯强, 吴庆农, 高俊峰, 等. 2002. 太湖地区的水资源与水环境——问题、原因与管理[J]. 自然资源学报, 2002, 17(2): 221–228.
DOI:10.3321/j.issn:1000-3037.2002.02.015 |
唐金艳, 曹培培, 徐驰, 等. 2013. 水生植物腐烂分解对水质的影响[J]. 应用生态学报, 2013, 24(1): 83–89.
|
王蓉, 黄天寅, 吴玮, 等. 2016. 典型城市河道氮、磷自净能力影响因素[J]. 湖泊科学, 2016, 28(1): 105–113.
|
王冼民, 翟淑华, 张红举, 等. 2017. 基于水质改善目标的太湖适宜换水周期分析[J]. 湖泊科学, 2017, 29(1): 9–21.
|
吴海明. 2011.表面流人工湿地处理北方污染河水的长期净化效果及相关机理研究[D].济南: 山东大学
|
吴鹏, 陆爽君, 徐乐中, 等. 2017. 改性沸石湿地脱氮除磷效能及机制[J]. 环境科学, 2017, 38(2): 580–588.
|
徐斌, 杨悦锁, 王咏, 等. 2017. 生态修复工程条件下污染河流水质模拟和应用[J]. 应用生态学报, 2017, 28(8): 2714–2722.
|
张秉文. 2012. 天然河道糙率计算及取值方法[J]. 南水北调与水利科技, 2012, 10(1): 25–28.
|
张惠, 汪鹏合, 张文娟, 等. 2017. 利用不同物候期水生植物配置提高浮床人工湿地的除氮效果[J]. 湖泊科学, 2017, 29(3): 575–584.
|
郑爽, 吴一红, 白音包力皋, 等. 2017. 含水生植物河道曼宁糙率系数的试验研究[J]. 水利学报, 2017, 48(7): 874–881.
|
 2018, Vol. 38
2018, Vol. 38


