随着经济的高速发展、城市化工业化的快速推进, 长三角地区正面临着日益严峻的大气污染问题(Chan and Yao, 2008).密集的城市布局及大量的工业、生活、交通污染的排放, 使得区域性复合型大气污染问题尤为突出.尤其是污染物在邻近城市或区域间的传输问题给大气污染控制与管理带来了巨大的压力与挑战(Li et al., 2013).
针对长三角地区开展大气污染物跨区域输送特征研究, 亟需对长三角区域污染因素进行详细分析, 深入认识该区域大气污染的来源和形成机理.由于大气污染物浓度模拟过程的高度非线性及各种因素的耦合关系, 需要对大量的减排情景进行评估比较, 传统的逐一评估方法往往面临效率低下的困境, 高额计算成本及低效的分析方法成为其现实应用的瓶颈(邢佳, 2011;戴志翔等, 2017).针对上述局限, 很多研究人员试图建立大气污染可控源排放-复合污染水平的函数关系(邢佳, 2011; 劳苑雯等, 2012), 实现给定排放情景的环境浓度实时响应, 以研究相关区域污染物排放场景与环境浓度之间的对应关系, 更好的服务大气污染物预测与减排效果评估等任务(戴志翔等, 2017).
目前已出现的大气污染可控源排放-污染物水平响应模型多采用响应曲面模型(Myers and Montgomery, 2008)(RSM).邢佳借助仿真实验手段, 建立了大气污染物排放-空气质量曲面响应模型, 并采用交叉验证、外部验证和等值线验证的方法对RSM系统的可靠性进行了评估(邢佳, 2011).劳苑雯基于CMAQ模型结果, 利用高维克里金插值算法, 建立了排放控制因子与污染物环境浓度的响应面模型(劳苑雯等, 2012), 实现了大气污染可控源排放与复合污染水平的实时函数响应, 并基于所建立的RSM开发了RSM-VAT区域大气污染控制可视化辅助决策工具.戴志翔等基于CMAQ模拟结果, 统计、归纳出各种污染物排放控制因子与污染物浓度间的函数关系, 建立空气质量响应曲面模型RSM, 实现了空气质量响应曲面模型在杭州市的应用(戴志翔等, 2017).
神经网络等统计机器学习方法已成为研究空气污染预测的有效工具之一(尹文君等, 2015; 白鹤鸣等, 2013).现有研究主要通过在不同时间节点下采样各影响因素, 如气象条件、排放活动、日期要素等, 及相应的环境污染物浓度情况建立各影响因子与污染物浓度之间的非线性关系(徐凌雁, 2015; 马晓光, 胡非, 2004).本文基于大气化学模型(CMAQ)的有限计算数据提供所选影响因子变化空间中大气污染物浓度预测与评估的方法.简单起见, 本文主要对PM2.5一种污染物浓度的响应进行详细计算分析, 同时验证了本方法对于其他污染物的适用性, 其他污染物的具体计算预测方法类似.
2 前置方法(Preposition method) 2.1 CMAQ模型与模型设置实际大气中各种污染物之间能够发生复杂的化学反应, 许多污染问题之间相互联系, 并且气象因素对大气污染问题具有重要影响(Byun and Schere, 2006).因此, 在20世纪90年代末, 美国国家环境保护局(EPA)研发了基于“一个大气”理念的第三代空气质量模式系统(Models-3/CMAQ)(Byun, 1999), 它是一个多尺度网格嵌套的三维欧拉模型, 能够实现多物种和多污染问题的同时模拟, 对于大气中各种物理化学过程描述更加全面.通过对CMAQ模型中排放清单相应污染物设置排放(减排)系数, 可以得到快速响应模型的输入数据.本文采用的CMAQ模型为CMAQv5.0.2版本, 模拟区域采用Lambert投影坐标系(Otte and Pleim, 2010), 坐标原点位置为34°N, 110°E.模拟采用三层嵌套网格(图 3), 第一层网格覆盖整个中国及东亚部分地区, 网格分辨率为36 km, 网格数为173×136.第二层网格覆盖中国东部, 网格分辨率为12 km, 网格数为135×228.第三层网格覆盖整个长三角, 网格分辨率为4 km, 网格数为150×174.由外层网格向内层提供边界数据与初始场, 最终模拟结果为第三层长三角区域的污染物浓度数据.
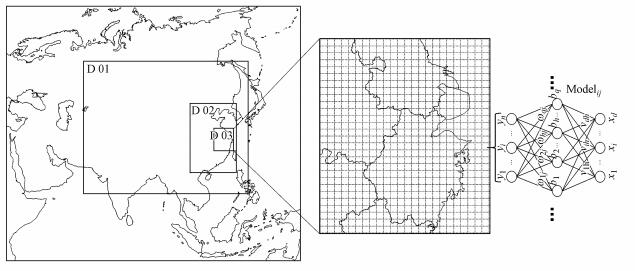 |
| 图 3 CMAQ模拟区域与神经网络模型长三角PM2.5预测示意图 Fig. 3 Schematic of CMAQ simulation region and PM2.5 prediction by neural network model |
神经网络的全称是人工神经网络(artificial neural network, ANN), 是在现代神经生物学研究成果的基础上发展起来的一种模拟人脑信息处理机制的网络系统(Schalkoff, 1997).其输入输出关系可描述为:
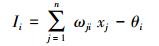
|
(1) |
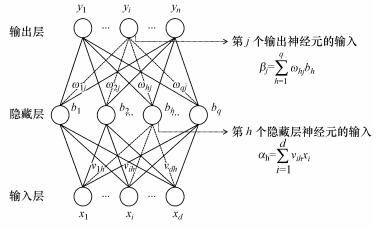 |
| 图 1 前馈神经网络结构示意图 Fig. 1 Structure diagram of feedforward neural network |

|
(2) |
式中, xj (j=1, 2, …, n)是从其他细胞传来的输入信号; θi为阈值; wji表示从细胞j到细胞i的连接权值;f称为传递函数.
前馈神经网络算法的原理是将模拟输出值和期望输出值的误差平方和作为神经网络的误差, 使用了统计机器学习中的极大似然估计思想(Nasrabadi, 2007; 李航, 2012).通过将误差反向传播, 从输出层传递至输入层, 采用梯度下降的方法调整网络权值和阈值, 具体参数更新流程如图 2所示.
 |
| 图 2 神经网络参数更新流程图 Fig. 2 Schematic of neural network parameter update |
从决策目的出发, 本研究关心的是长三角不同区域相关污染物排放对长三角PM2.5污染的影响.考虑到模型复杂度的约束, 控制因子数量的增加将导致计算所需样本数量迅速增加, 从而提高模型计算复杂度(邢佳, 2011), 本研究控制因子基于PM2.5污染前体物种类以及排放源地区, 选取来自长三角主要省市的各种污染物中相对效能较大的因子.由于PM2.5来源中一次微粒与污染物浓度的响应关系基本为线性, 而二次气溶胶组分的非线性特征最为明显(Zhao et al., 2015), 我们选取各区域PM2.5一次污染物总量作为线性控制因子, 各区域的NOx、SO2、NH3、VOC及POA排放强度等作为非线性控制因子(戴志翔等, 2017).长三角主要地区按照省份划分为:A上海, B江苏, C浙江, D安徽以及E其他区域.通过将5个区域和6种主要影响污染物两两组合一共生成了A_NOX_TT, A_SO2_TT……等30个长三角区域PM2.5污染物浓度的主要影响因子.
对于参数水平的设置, 约定参数水平等于目标年排放量与基准年(2014年)排放量的比值.通过在CMAQ输入排放源清单中设置基于基准水平的乘数因子得到不同的污染物排放场景.参数水平为1, 表示目标年与基准年排放量相同, 不做控制;0为最小值, 代表没有可控源污染物排放;可控源污染物如果在目标年排放量增大, 则其参数水平将大于1.表 1所示即为选取的控制因子及相应的参数水平汇总.
| 表 1 长三角PM2.5快速响应模型的控制因子 Table 1 Control factors of YRD PM2.5 fast response model |
对于表 1中的PM25_TT线性控制因子, 由于响应关系是线性的, 所以只需对每个控制因子在0和1两种控制情景下分别进行CMAQ模拟, 即可获得求解该线性响应关系所需的实验样本.对于NOx_TT, SO2_TT, NH3_TT, VOC_TT, POA_TT这5个非线性控制因子, 设定它们的参数水平变化范围为0~2.
3.2 采样方法根据拉丁超立方采样方法(LHS, Latin hypercube sampling)(Iman, 2008; Pilz and Spöck, 2008), 生成了建立快速响应模型所需要的实验矩阵, 即为包含1个基本算例(所有控制因子的参数水平均设置为1)和367个控制算例(编号2~368)的实验设计方案, 同时为了验证快速响应模型对于外部样本的泛化预测能力, 我们另外选取并计算了30种排放方案(编号403~432)作为模型检验测试集, 共398个算例, 实验方案设计如表 2所示.
| 表 2 LHS实验方案设计 Table 2 LHS experimental design |
将表 2所示实验矩阵作为输入依据, 通过对原始CMAQ模拟输入区域污染物排放比例参数进行相应设置, 在并行计算机群上进行398次CMAQ模拟计算, 获取了待研究区域在研究控制情景下2014年1月1日—2014年1月31日的大气污染物浓度数值模拟结果.根据研究的需要提取了长三角主要区域2014年1月31日中午12:00时间截面的PM2.5浓度的数据, 从而获得了398个经过采样的长三角区域PM2.5浓度分布训练与验证数据集.为了检验神经网络模型在一天的不同时段以及对于不同污染物浓度预测方面的效果, 同时提取了2014年1月31日凌晨00:00时间截面的PM2.5浓度及2014年1月31日中午12:00时间截面的O3浓度相关数据用于进行对比研究.
4 模型建立(Establishment of model) 4.1 前馈神经网络模型结构确定使用前述影响区域PM2.5污染浓度的30个影响因子作为输入, 将CMAQ模拟得到的区域PM2.5浓度网格值作为输出建立PM2.5的快速响应模型.若将整个区域的PM2.5浓度值作为输出构建模型将产生十分巨大的网络结构, 这将使得网络的参数更新计算量变得十分巨大, 同时当训练样本数远少于参数数量时神经网络模型极易出现过拟合现象(Nasrabadi, 2007; 李航, 2012).考虑到输出区域的局部PM2.5浓度值存在相关性, 同时为了使得模型结构和参数量更为合理, 将输出的PM2.5区域浓度进行部分离散化处理, 适当保留污染物浓度局部相关性并减少离散化对于整个区域污染物浓度之间相关性的影响, 将整个长三角区域网格划分为若干6×5网格的矩形小区域(如图 3所示), 对每一个小区域的PM2.5浓度和输入影响因子的非线性关系通过单个前馈神经网络Modelij进行建模.得到若干局部区域模型后, 按照顺序组合成为最终预测模型.
考虑到输入输出维度及训练样本数, 神经网络的结构考虑采用最常用的单隐藏层前馈神经网络, 隐藏层数量根据以下经验公式(Krogh and Vedelsby, 1995):

|
(3) |
式中, ni, nh, no分别为输入层、隐藏层、输出层的节点个数, α为常数并且0≤α≤20.ni和no根据前文所述均为30.选取α=20, 计算得到nh=50, 即确定神经网络结构为输入输出层30个节点, 隐藏层为50个节点.
3.2 神经网络模型训练考虑到神经网络输出为30维局部污染物浓度值, 使用均方误差作为神经网络训练损失函数(Nasrabadi, 2007; 李航, 2012):
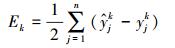
|
(4) |
式中, Ek为误差值, n表示局部网格数, 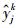
根据输入输出数据数量, 采用批量梯度下降算法对神经网络参数进行训练, 为了克服神经网络模型易产生过拟合的情况, 对经过不同训练次数的神经网络模型进行外部验证(戴志翔等, 2017; Santner, Williams and Notz, 2013), 最终确定最佳训练迭代次数.神经网络模型的激活函数选择Sigmoid函数, 采用学习速率自适应的Adagrad梯度下降法(Duchi, 2011), 假设某次迭代时刻t, gt, i=∇θj(θi)是目标函数对参数的梯度, 则参数的下一个迭代值为:
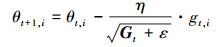
|
(5) |
式中, 
前馈神经网络模型与作为对照的RSM模型两种方法所使用的数据完全一致, 两种模型所运行的硬件条件也基本相同.RSM模型使用的是中国空气污染控制成本效益与达标评估系统(ABaCAS)中实时空气质量模拟可视化分析工具(RSM-VAT/CMAQ)模块(劳苑雯等, 2012; Zhu et al., 2015)的1.10版本, 前馈神经网络模型所采用的平台是通过python的Pytorch-Gpu(Paszke et al., 2017)搭建的神经网络模块, 所共用的硬件配置如表 3所示.
| 表 3 硬件软件配置 Table 3 Configuration of hardware and software |
为了全面地评估神经网络响应模型预测值与CMAQ模拟值的近似程度并和RSM模型的预测结果进行对比, 我们利用外部验证方式并结合平均偏差(MB)、平均误差(ME)、标准平均偏差(NMB)、标准平均误差(NME)、平均相对偏差(MFB)和平均相对误差(MFE)等统计指标(Dixon et al., 1957)对于模型预测能力进行校验.对于每个统计指标, 还根据30个外部验证样本对其统计了平均值(mean)、最大值(max)、最小值(min)以反映其综合性能.同样方式对RSM模型模拟结果的相关统计指标进行计算, 两种模型的统计指标结果如表 4所示.
| 表 4 神经网络模型与RSM模型统计指标对比 Table 4 Statistical index comparison between neural network model and RSM model |
从表中可以看出, 神经网络模型对于CMAQ的预测是相对准确的, 30个外部样本的MB均值达到了-0.046 μg·m-3, ME均值也达到了0.6162 μg·m-3, 这意味着平均每个格点的PM2.5浓度预测值的误差绝对值小于1 μg·m-3, 这种数量级的误差对于区域空间尺度的污染物浓度预测可以接受.其余统计指标也都显示神经网络模型对于误差抑制方面的成功, 其NMB、NME、MFB、MFE在30个样本中的均值分别达到了-0.08%、1.27%、0.12%和0.75%, 在和RSM模型相应指标的相应对比中表现更好.
图 4为在6个外部验证工况下CMAQ模型原始预测值与神经网络模型的对比, x轴表示CMAQ模型得到的每个网格值的模拟值, y轴表示NN-1250模型(经过1250次迭代的神经网络模型)得到的每个网格的预测值, 红色的斜线代表所需要拟合的直线, 相关系数CORR表征拟合相关性(Dixon et al., 1957), CORR越接近1代表两者的相关性越好, 6个验证情境下的相关系数分别为0.9998、0.9998、0.9998、0.9998、0.9997和0.9986, 神经网络响应模型的预测值与CMAQ模拟值在每个网格节点上都具有良好的一致性.
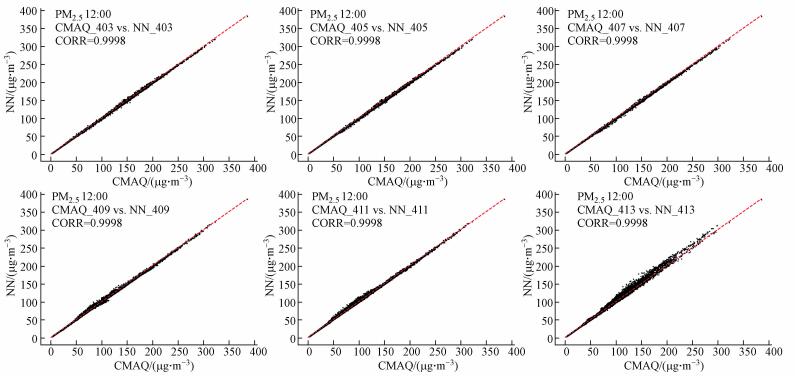 |
| 图 4 外部验证情景下各格点污染物浓度拟合散点图 Fig. 4 Grid PM2.5 fitting scatterplot in external verification scenarios |
为检验神经网络模型在更多预测情况(不同时段, 不同污染物)下的适用性, 本文对于2014年1月31日00:00的PM2.5浓度预测及2014年1月31日12:00的O3浓度的预测同样进行了计算, 所得结果如图 5所示.
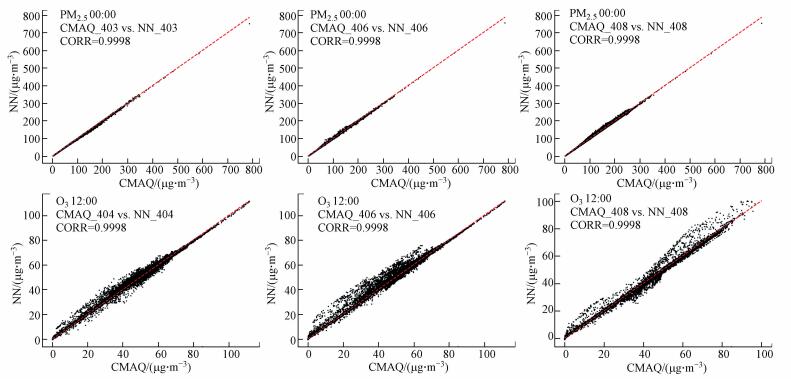 |
| 图 5 00:00时段PM2.5与12:00时段O3浓度外部验证情景污染物浓度拟合散点图 Fig. 5 Grid fitting scatterplot of PM2.5 and O3 in external verification scenarios |
可以看到, 在不同时段的PM2.5浓度预测中, 神经网络模型预测结果和CMAQ模拟结果的网格节点污染物浓度相关系数均达到0.999, 说明在不同时段下神经网络模型仍然具有良好的预测效果.在对于另一种污染物O3的预测情况中, 神经网络模型的预测准确度也达到0.99以上, 拟合准确程度较PM2.5存在一定波动.考虑到本文在选择污染物影响因子的时候主要考虑的是PM2.5, 并设置了专门针对PM2.5浓度的线性控制因子, 控制因子设置对于其他污染物并不完全准确, 达到这样的预测准确程度已经能够说明其对其他污染物浓度的快速响应能力.
5.3 神经网络模型与RSM模型预测效果对比我们在计算过程中分别计算了迭代(神经网络参数更新次数)250、500、750…直到3000次时神经网络模型的统计指标并与RSM模型进行了对比, 如图 6所示.
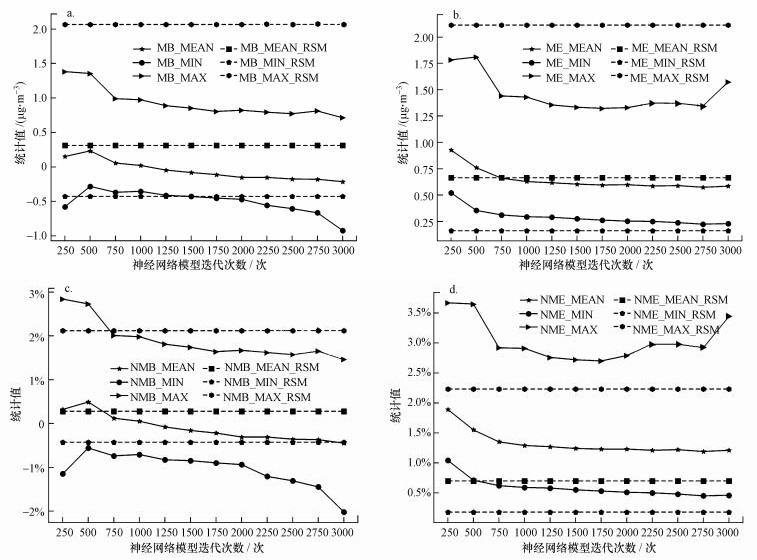 |
| 图 6 不同迭代次数下神经网络模型与RSM模型统计指标对比图(a.MB, b.ME, c.NMB, d.NME) Fig. 6 Comparison of statistical parameters between neural network model and RSM model under different iterations(a.MB, b.ME, c.NMB, d.NME) |
从前馈神经网络模型和RSM模型对于CMAQ结果的预测比较图可以看出, 前者的相关统计指标在经过250次左右的迭代之后便和RSM模型达到了同一数量级, 显示出优良的计算拟合速度.同时前者的平均误差(ME)和平均偏差(MB)均值(30个外部验证工况下)的绝对值在1250参数迭代更新后达到一个较为稳定的状态, 分别达到了0.046 μg·m-3和0.6162 μg·m-3, 优于RSM模型的0.3109 μg·m-3和0.6638 μg·m-3, 而ME和MB的最大(小)值也都再经过1000~1250次迭代之后达到理想值, 显示出神经网络模型在对极值抑制方面的优势.而继续训练并不能使相关统计指标得到继续优化, 相反, MB和ME在外部样本中的统计值都在约2000次迭代之后出现了震荡转劣现象, MB均值的绝对值上升到了0.1528 μg·m-3, 这一部分的训练进入到了机器学习中常见的过拟合区间(Nasrabadi, 2007; 李航, 2012).
在神经网络模型的其余统计指标随训练次数变化的曲线中也都出现了类似现象, 在这里我们采用机器学习神经网络训练中常用的过拟合防止方法:早停(Nasrabadi, 2007).选取迭代次数为1250次时的神经网络模型作为最终预测模型, 这样既能减少过拟合的风险又能提高训练的效率, 本文所述神经网络模型及其预测值均采用了这一模型.
图 7是第413个外部验证排放工况下长三角区域PM2.5浓度预测及其与CMAQ模型模拟值和RSM预测值的相关对比.从图中可以看到神经网络模型预测的结果和CMAQ模型模拟得到的浓度分布十分接近, 实现了对其模拟的高度还原.RSM模型和神经网络模型在响应预测方面都达到了不错的效果, 神经网络模型在误差极值抑制方面做得比较出色, 误差上下限均优于RSM预测值, 而RSM模型在浓度预测的平滑性方面具有优势, 两者在浓度变化复杂区域的预测方面都有不小的改进空间.针对浓度变化复杂区域预测偏差较大的情况, 在增加计算复杂度的前提下, 神经网络模型可以通过对特定区域选取不同离散方式(选取不同矩形小区域构建神经网络模型)求均值的方法增加预测的准确度与平滑性, 考虑到计算复杂度与准确度的必要性本文并未采取.
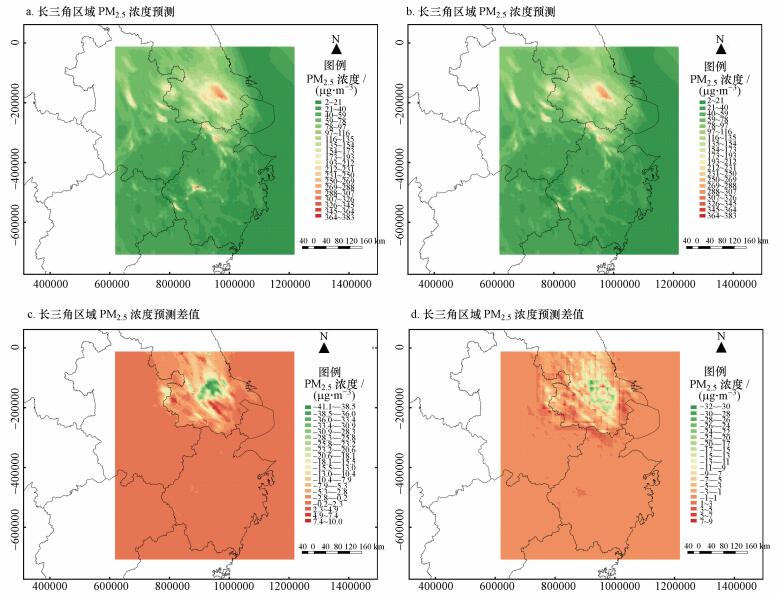 |
| 图 7 #413外部验证样本长三角区域神经网络模型PM2.5浓度预测分布及相关对比(a. CMAQ模型, b.神经网络模型, c. RSM-CMAQ, d.神经网络-CMAQ) Fig. 7 PM2.5 concentration predictive in YRD region based on neural network model of 413th external validation sample |
在两种模型的计算时间效率方面, 使用RSM模型的RSM-VAT软件在处理具有368个输入样本时完整计算时间需要8 h左右, 而神经网络模型在达到较优解的1250次迭代计算只需要30 min, 神经网络模型在计算速度方面优势明显.
从计算结果来看, 基于前馈神经网络的快速响应模型在计算精确度和模型生成速率方面都能得到肯定, 但从使用便捷度来说依然存在不小的挑战, 比如神经网络的结构设计及参数更新方法等都需要一定经验, 神经网络模型过拟合问题易发(Lawrence et al., 2000)等.不过从本文的计算过程可以看出其中一些关键点:影响因子的选取、初始CMAQ样本的合理采样、基于输入变量数的计算区域局部离散化、模型复杂度控制以及计算迭代次数的适当选取等.基于统计机器学习的方法在大气污染物浓度快速预测方面具有很大的潜力.
5 结论(Conclusions)1) 基于前馈神经网络的长三角区域PM2.5快速响应模型能够快速准确预测特定排放控制措施下污染物浓度的预测, 神经网络模型在每个网格节点外部验证结果的平均相关度(CORR)达到了0.999以上.神经网络模型的平均误差(ME)和平均偏差(MB)均值(30个外部验证情景下)分别达到了0.046 μg·m-3和0.6162 μg·m-3.
2) 在神经网络模型达到稳定之后, 在大部分的模型评价指标中比RSM模型表现更好, 显示出前馈神经网络作为一种通用非线性函数拟合器的良好性能.从快速响应模型生成的时间效率来看, 得益于良好的结构设计与训练策略, 神经网络模型经过250次左右后预测误差便能达到与RSM相同的数量级, 在模型生成速度方面同样优势明显.
3) 通过对不同时段PM2.5及相同时段O3浓度预测计算比较, 前馈神经网络模型在污染物浓度预测方面的普适性得到验证.神经网络模型在误差极值抑制方面的表现较好, 误差上下限均优于RSM预测值, 而RSM模型在浓度预测的平滑性方面具有优势, 两者在浓度变化较为复杂区域的污染物浓度预测方面都存在改进空间.统计机器学习方法在大气污染物浓度实时快速预测方面具有潜力.
Byun D. 1999. Science algorithms of the EPA Models-3 community multiscale air quality (CMAQ) modeling system[J]. EPA/600/R-99/030
|
Byun D, Schere K L. 2006. Review of the governing equations, computational algorithms, and other components of the Models-3 Community Multiscale Air Quality (CMAQ) modeling system[J]. Applied mechanics reviews, 59(2): 51–77.
DOI:10.1115/1.2128636
|
白鹤鸣, 沈润平, 师华定, 等. 2013. 基于BP神经网络的空气污染指数预测模型研究[J]. 环境科学与技术, 2013, 36(3): 186–189.
|
Chan C K, Yao X. 2008. Air pollution in mega cities in China[J]. Atmospheric Environment, 42(1): 1–42.
|
戴志翔, 胡诗玮, 罗坤, 等. 2017. 空气质量响应曲面模型在杭州市的应用[J]. 中国科学院大学学报, 2017(2): 179–185.
|
Dixon W J, Massey Jr F J. 1957. Introduction to statistical analysis[Z].
|
Myers R H, Montgomery D C. 2008. Response Surface Methodology:Process and Product in Optimization Using Designed Experiments[J]. Technometrics, 38(3): 284–286.
|
Duchi J, Hazan E, Singer Y. 2011. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 12(Jul): 2121–2159.
|
Iman R L. 2008. Latin hypercube sampling[J]. Wiley StatsRef: Statistics Reference Online
|
Krogh A, Vedelsby J. 1995. Neural network ensembles, cross validation, and active learning[Z]. 231-238
|
Lawrence S, Giles C L. 2000. Overfitting and neural networks: conjugate gradient and backpropagation[Z]. IEEE. 114-119
|
Li J, Wang Z, Huang H, et al. 2013. Assessing the effects of trans-boundary aerosol transport between various city clusters on regional haze episodes in spring over East China[J]. Tellus Series B-Chemical And Physical Meteorology, 65(20052).
|
劳苑雯, 朱云, CareyJang, 等. 2012. 基于响应面模型的区域大气污染控制辅助决策工具研发[J]. 环境科学学报, 2012, 32(8): 1913–1922.
|
李航. 2012. 统计学习方法[M]. 北京: 清华大学出版社.
|
马晓光, 胡非. 2004.利用支撑向量机预报大气污染物浓度[Z].
|
Nasrabadi N M. 2007. Pattern recognition and machine learning[J]. Journal of Electronic Imaging, 16(4): 49901.
DOI:10.1117/1.2819119
|
Otte T L, Pleim J E. 2010. The Meteorology-Chemistry Interface Processor (MCIP) for the CMAQ modeling system:updates through MCIPv3. 4.1[J]. Geoscientific Model Development, 3(1): 243–256.
DOI:10.5194/gmd-3-243-2010
|
Paszke A, Chintala S, Collobert R, et al. Pytorch: Tensors and dynamic neural networks in python with strong gpu acceleration, may 2017[Z].
|
Pilz J, Spöck G. 2008. Why do we need and how should we implement Bayesian kriging methods[J]. Stochastic Environmental Research and Risk Assessment, 22(5): 621–632.
DOI:10.1007/s00477-007-0165-7
|
Santner T J, Williams B J, Notz W I. 2013. The design and analysis of computer experiments[M]. Springer Science & Business Media
|
Schalkoff R J. 1997. Artificial neural networks[M]. McGraw-Hill New York.
|
邢佳. 2011.大气污染排放与环境效应的非线性响应关系研究[D].北京: 清华大学
http://cdmd.cnki.com.cn/Article/CDMD-10003-1012035908.htm |
徐凌雁. 2015. 基于粗糙集的BP神经网络空气品质预测模型[J]. 东北电力大学学报, 2015, 35(5): 81–87.
DOI:10.3969/j.issn.1005-2992.2015.05.016 |
尹文君, 张大伟, 严京海, 等. 2015. 基于深度学习的大数据空气污染预报[J]. 中国环境管理, 2015(6): 46–52.
DOI:10.3969/j.issn.1674-6252.2015.06.011 |
Zhao B, Wang S X, Xing J, et al. 2015. Assessing the nonlinear response of fine particles to precursor emissions:development and application of an extended response surface modeling technique v1.0[J]. Geoscientific Model Development, 8(1): 115–128.
DOI:10.5194/gmd-8-115-2015
|
Zhu Y, Lao Y, Jang C, et al. 2015. Development and case study of a science-based software platform to support policy making on air quality[J]. Journal of Environmental Sciences, 27: 97–107.
DOI:10.1016/j.jes.2014.08.016
|
 2018, Vol. 38
2018, Vol. 38


