2. 中国海洋大学海洋环境与生态教育部重点实验室, 青岛 266100
2. Key Laboratory of Marine Environment & Ecology, Ministry of Education, Ocean University of China, Qingdao 266100
近年来, 受工农业活动的影响, 污水和固体废物的排放量大幅增加, 导致地下水发生了不同程度的污染(王曼丽等, 2016).地下水质量评价是水利规划、水资源合理开发利用和管理的基础.在地下水质量评价过程中, 地下水的质量类别是客观存在的模糊事物(马玉杰等, 2009).依据客观的评价标准与实测值, 模糊数学评价法通过模糊变换的原理对模糊概念(事物、现象)进行评价, 可以解决此类具有模糊性的环境评价(杨伦标等, 2011).
模糊综合评价法(Filev et al., 1998)和可变模糊集方法(Wang et al., 2014)是地下水质量评价中常用的模糊数学评价法, 成为国内外的研究热点(张祺等, 2015;Yan et al., 2014;李云排等, 2014;Yan et al., 2016).通过模糊变换, 模糊综合评价法给出评价对象与标准等级间的隶属关系, 具有可变参数少、计算简便的优点.但采用最大隶属度原则得出的评价级别, 容易造成隶属度信息丢失, 并存在不适用的评价条件(陈守煜, 1998).可变模糊集方法以相对差异函数为基础, 得出评价对象与标准等级间的隶属关系, 充分利用了隶属度信息, 使评价结果更加准确.但可变模糊集评价方法存在计算复杂、可变参数多、单因子极值评价片面等缺陷(冯峰等, 2007).
因此, 本研究吸取模糊综合评价法和可变模糊集方法的优点, 构建新的耦合评价模型, 并优化水质评价过程中评价因子选择、权重确定、模糊算子选择等关键环节, 最后对青岛市大沽河水源地的地下水质量进行评价和分析对比, 以期为地下水资源保护和管理提供科学的依据.
2 模糊综合与可变模糊集耦合模型的构建(The hybrid model based on fuzzy synthetic evaluation and variable fuzzy sets) 2.1 模糊综合评价方法模糊综合评价法依据最大隶属度原则给出评价对象与标准等级间的隶属关系, 主要步骤如下(Yang et al., 2016;韩玮等, 2015).①建立模糊关系矩阵.利用隶属度函数求出各评价因素ui对于各评价等级vj的隶属度, 得到单因素模糊关系矩阵R.隶属度函数多用“隶属度-浓度”关系来表示, 考虑到运算的实际性, 一般采用“降半梯形分布法”(Yan et al., 2014)来计算.②计算模糊综合评价结果向量.模糊综合评价结果向量由权重矩阵A和模糊关系矩阵R做复合运算得到(式(1)).③确定评价对象的评价等级.根据最大隶属度原则, 取bi=max(b1, b2, …, bm), 即得相应的综合评价等级为Vi.
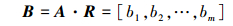
|
(1) |
式中, B为评价结果向量;“·”为模糊算子.
2.2 可变模糊集方法设模糊概念集合U中的任意元素u, 对吸引区间A的相对隶属度为μA(u), μAc(u)∈[0, 1];对排斥区间Ac的相对隶属度为μAc(u), μAc(u)∈[0, 1].设:
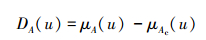
|
(2) |
式中, DA(u)称为模糊概念u对吸引区间A的相对差异度.其中:
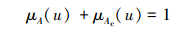
|
(3) |
由式(2)、(3), 可求解相对隶属度μA(u):
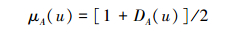
|
(4) |
在隶属度连续数轴上(图 1), 设X0=[a, b]为模糊概念u的吸引区间, X=[c, d]为包含X0的某一上、下界范围区间(李文君等, 2011).
 |
| 图 1 区间[a, b]、[c, d]与点x、M的位置关系 Fig. 1 The drawing of position relation between zone [a, b], [c, d] and point x, M |
由定义可知, [c, a]和[b, d]均为模糊概念u的排斥域, M为吸引区间[a, b]中相对隶属度μA(u)=1的点.设x为X区间内的任意一点, 当x落入M点左侧时, 其相对差异度函数如式(5)所示(陈守煜等, 2006);当x落入M点右侧时, 其相对差异度函数如式(6)所示.
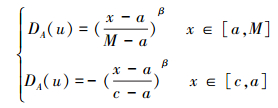
|
(5) |
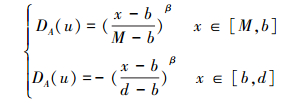
|
(6) |
通常β=1, 即相对差异度函数模型为线性模型.将式(5)或式(6)得到的相对差异度值DA(u)代入式(4), 可求解相对隶属度μA(u), 从而得到单因素模糊关系矩阵R.
设有n个评价指标, 评价等级数为m, 则可变模糊集评价模型为(Wang et al., 2014):
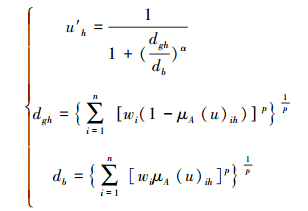
|
(7) |
式中, uh′为样本关于级别h的非归一化综合相对隶属度;h为评价等级, h=1, 2, 3, …, m;dgh、db为相对隶属度对左、右极点的广义权距离;μA(u)ih为评价指标i对等级h的相对隶属度;p为模型可变距离参数, p=1, 2;α为模型可变优化准则参数, α=1, 2;wi为评价指标i的权重(薛希龙等, 2016).对相对隶属度uh′进行归一化处理, 并进一步确定评价等级, 其公式为:
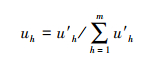
|
(8) |
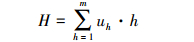
|
(9) |
式中, uh为样本关于级别h的归一化综合相对隶属度;H为评价对象的等级;h的含义及取值与公式(7)相同.
2.3 模糊综合与可变模糊集耦合评价模型模糊综合评价和可变模糊集两种方法的本质均是计算评价对象与标准等级间的隶属关系.基于此, 结合两种方法的优点, 构建新的评价模型.
2.3.1 评价指标集U的建立依据《地下水质量标准》(DZ/T 0290-2015), 从地下水水质常规监测指标中选取合适的指标, 作为地下水水质综合评价指标.但在水质综合评价中, 当低于或等于一类水质标准值的指标(环境影响极小的因子)过多时, 这些指标会“削弱”环境影响较大的因子对水质评价结果的影响.
另一方面, 当前水质评价中常用的指标筛选方法是累积频率法, 将各指标的超标倍数从大到小排列, 选择累加之和不低于85%的因子(环境影响较大的因子)作为评价指标.而缺少环境影响相对较小的因子(实测值超过一类水质标准值, 且处在累积频率不低于85%范围外的指标), 使评价结果较差, 达不到综合评价的要求.基于以上考虑, 结合综合评价中对评价指标全面、重点突出的要求, 可做如下筛选.
将《地下水质量标准》(DZ/T 0290-2015)中常规监测指标集作为初选指标, 若某初选指标在所有取样点的实测值均小于或等于一类水质标准值, 则去除该指标, 即:
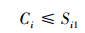
|
(10) |
式中, Ci为第i个指标的实测值;Si1为第i个指标的一类水质标准值.
应用该方法对评价指标进行筛选, 可以去除某些环境影响极小的因子, 又体现了环境影响相对较小的因子对水质评价结果的影响.
2.3.2 评语集V的确定选择《地下水质量标准》(DZ/T 0290—2015)为评判标准, 故V={1, 2, 3, 4, 5}.
2.3.3 模糊关系矩阵R的建立模糊综合评价法在隶属度计算上具有可变参数少、计算简便的优点, 因此, 耦合模型借鉴模糊综合评价采用“降半梯形分布法”得到单因素模糊关系矩阵R.
2.3.4 评价因子权重矩阵A的确定指标权重是评价指标在地下水水质评价中的相对重要程度, 从某种角度说, 也是评价指标的危害性大小.水质评价中, 权重的确定方法有多种, 而聚类权法在确定权重时, 既考虑了地下水质量标准各类标准值变化幅度的差异性, 又考虑了样本的指标实测值, 在地下水质量评价中具有合理性(李录娟等, 2014).因此, 耦合模型选择聚类权法确定指标权重, 计算公式为:
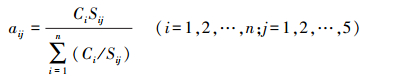
|
(11) |
式中, aij为评价指标i在等级j的权重;Ci为指标i的实测值;Sij为指标i在等级j的标准值.
2.3.5 评价结果向量B的计算由权重矩阵A和模糊关系矩阵R做复合运算得到评价结果向量B(式(1)), 其中, 模糊算子通常有4种类型, 分别为:取小取大法、相乘取大法、相乘相加法和取小相加法.只有相乘相加法是“加权平均型”的评价(傅金祥等, 2011), 该方法依据指标权重对单因素隶属度信息均衡兼顾, 充分利用了所有评价信息.故耦合模型采用第3种方法—“加权平均型”算子, 计算公式为:
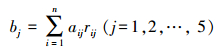
|
(12) |
式中, bj为评价对象关于级别j的非归一化综合隶属度.
2.3.6 评价对象的评价等级的确定可变模糊集理论在确定评价对象的评价等级时, 充分利用了隶属度信息.因此, 耦合模型借鉴可变模糊集理论确定评价对象的评价等级, 即:由2.3.5节得到复合运算矩阵B=A·R=[b1, b2, …, b5];b1、b2、…、b5均为样本关于评价等级的非归一化综合隶属度, 对应式(8)中uh′;利用式(8)、(9), 计算评价对象的等级.
3 地下水质量评价与可靠性分析(Groundwater quality evaluation and reliability analysis) 3.1 地下水水质大沽河地下水水源地位于青岛市西北部, 是青岛市重要的供水水源.该区含水层主要是由砂和砂砾石组成, 厚度一般为4~8 m;含水层之上以粘质砂土为主, 砂质粘土次之, 厚度一般为2~5 m, 南北两端多为3~5 m, 地下水主要贮存于第四纪砂层, 属于潜水含水层(图 2).补给方式以大气降水补给为主, 工农业开采是主要的排泄方式.
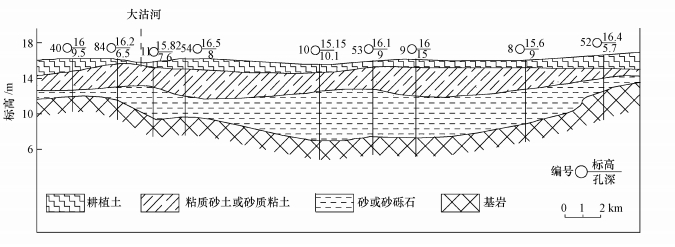 |
| 图 2 青岛市大沽河地下水水源地水文地质剖面示意图 (A-A′剖面, 图 3) Fig. 2 Diagrammatic cross-section of hydrogeology in the Dagu River watershed in Qingdao |
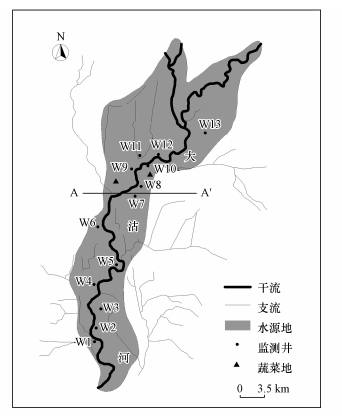 |
| 图 3 青岛市大沽河地下水水源地监测井站位图 Fig. 3 Location of monitoring wells in the Dagu River watershed in Qingdao |
本文以2014年丰水期(9月)青岛市大沽河地下水水源地内13口监测井(图 3)的潜水水质监测资料作为评价的原始数据, 各监测井化学指标值如表 1所示.水质监测资料由青岛市水环境监测中心提供, 遵照国家环境保护总局编制的《水和废水监测分析方法(第四版)》(2002年)对水样进行全分析.
| 表 1 大沽河水源地各监测井化学指标实测值 Table 1 Data of chemical analysis for each of the well in the Dagu River watershed |
应用耦合模型对青岛市大沽河地下水源地水质状况进行评价, 具体步骤如下.
3.2.1 评价指标集建立结果根据耦合模型指标选取的方法, 在大沽河地下水源地13口监测井中, pH、汞、砷、镉、铬(六价)、铅、挥发性酚类、铁、锌、铜、氰化物等指标实测值均未超出该指标一类水质标准值, 故去除这些指标.筛选出的评价指标为:总硬度、氯化物、溶解性总固体、硫酸盐、锰、高锰酸盐指数、氟化物、硝酸盐、氨氮、亚硝酸盐.评价标准采用《地下水质量标准》(DZ/T 0290—2015).
3.2.2 模糊关系矩阵R和权重矩阵A计算结果依据耦合模型计算隶属度的方法, 确定模糊关系矩阵R(以W1为例):
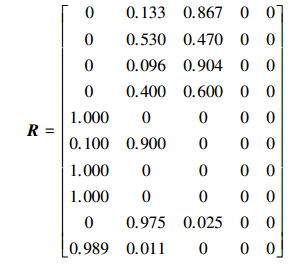
|
(13) |
式中, 第1行代表总硬度对5个等级的隶属度值;其余类推, 分别是氯化物、溶解性总固体、硫酸盐、锰、高锰酸盐指数、氟化物、硝酸盐、氨氮、亚硝酸盐对5个等级的隶属度值.依据式(11)得到权重矩阵A(式(14)).

|
(14) |
式中, 第1行代表总硬度对5个等级的权重值;其余类推, 分别是氯化物、溶解性总固体、硫酸盐、锰、高锰酸盐指数、氟化物、硝酸盐、氨氮、亚硝酸盐对5个等级的权重值.
3.2.3 评价结果向量B和评价等级H计算结果以W1为例, 运用式(12), 对模糊关系矩阵R和权重矩阵A进行复合运算, 得到评价结果向量B=A·R=(0.095, 0.407, 0.551, 0.000, 0.000).利用式(8)对向量B进行归一化处理, 得到归一化评价结果向量(0.090, 0.387, 0.523, 0.000, 0.000), 并运用式(9)得到评价等级H=2.433.为便于实际应用, 对等级值H采用进一法处理, 得到监测井W1的评价等级为3类.同理, 按照以上步骤, 可以得到其它12口监测井的评价等级(表 2).
| 表 2 各监测井评价结果 Table 2 Evaluation results for each of the well |
从计算角度看, 耦合模型较可变模糊集方法大大简化, 在实践中具有更强的应用性.与模糊综合评价法的评价结果(表 2)进行比较, 发现耦合模型的评价结果更加合理.具体分析如下.
应用模糊综合评价时, 从监测井W2、W3、W4、W7、W10、W11、W12获得的最大隶属度小于0.5, 说明模糊综合评价法不适用于这些点的水质评价.
以监测井W2为例, 评价结果向量(0.050, 0.085, 0.245, 0.240, 0.379)中, 取最大隶属度0.379, 属于5类水, 但忽略了该向量中其它隶属度对评价结果的影响.而在耦合模型中, 则综合考虑了其它隶属度值对评价结果的贡献, 得出水质等级为4类, 克服了模糊综合评价中隶属度信息丢失的缺陷.
根据监测井W6的水质资料, 总硬度和硝酸盐氮的实测值超过5类水质标准0.02倍, 溶解性总固体也介于3~4类之间, 而其它指标的水质等级均优于3类水.应用耦合模型进行评价, 其结果为4类水(H=3.777), 评价结果较为合理;而模糊综合评价得到的结果为5类水, 评价结果明显偏高.
以监测井W8和W9为例, 模糊综合评价得出的水质等级均为5类水, 无法区分二者水质的优劣.而耦合模型得出W8和W9的H值分别为4.181、4.380, 显然监测井W8的水质更好.对于水质等级相同的监测井而言, 耦合模型克服了模糊综合评价法不能对其综合水质进行比较的缺点, 在实际应用中具有显著的优越性.
水源地中北部(W7~W11)地区, 耦合模型得到的水质等级均为4或5类水, 水质状况较差, 其主要原因是硝酸盐氮含量严重超标(硝酸盐氮的实测值超过5类水质标准0.6~2.5倍).该区域地下水埋深较浅, 含水层岩性以粗砂、中粗砂为主, 上覆土层主要是砂和砂质亚粘土, 含水层渗透性好, 来源于地表的污染物容易下渗.而该区域是青岛市的主要蔬菜生产基地, 氮肥的过量使用和低效率利用, 使大量未被作物吸收的氮肥进入地下, 经生物地球化学作用, 转化为硝酸盐, 最终污染地下水.评价结果符合该区域实际水质状况, 说明耦合模型是可靠的.
4 结论(Conclusions)1) 本研究构建的耦合评价模型充分吸收了模糊综合评价法和可变模糊集方法的优点.在隶属度计算上, 借鉴模糊综合评价简化了运算;在确定评价等级时, 借鉴可变模糊集理论, 体现了各评价等级的隶属度对评价结果的贡献.同时, 进一步优化了评价指标筛选、指标权重确定、模糊算子选择等关键环节.
2) 应用模糊综合评价时, 从监测井W2、W3、W4、W7、W10、W11、W12获得的最大隶属度小于0.5, 说明该方法不适用于这些点的水质评价.而耦合模型综合考虑了其它隶属度值对评价结果的贡献, 克服了模糊综合评价中隶属度信息丢失的缺陷, 评价结果更加合理.
3) 水源地中北部(W7~W11)地区, 硝酸盐氮含量严重超标, 耦合模型得到的水质状况较差.农业生产活动中氮肥的大量施用及该区域的水文地质条件是导致地下水大面积硝酸盐污染的主要原因.耦合评价模型得到的结果符合该区域实际水质状况, 说明模型是可靠的.
陈守煜. 1998. 工程模糊集理论与应用[M]. 北京: 国防工业出版社.
|
陈守煜, 李敏. 2006. 基于可变模糊集理论的水资源可再生能力评价模型[J]. 水利学报, 2006, 37(4): 431–435.
|
Filev D, Yager R R. 1998. On the issue of obtaining OWA operator weights[J]. Fuzzy Sets and Systems, 94(2): 157–169.
DOI:10.1016/S0165-0114(96)00254-0
|
冯峰, 许士国, 周志琦, 等. 2007. 模糊可变评价法在湿地水质评价中的应用[J]. 人民黄河, 2007, 29(8): 41–42.
|
傅金祥, 陈喆, 马兴冠, 等. 2011. 改良模糊综合评价法在水质评价中的应用[J]. 环境工程, 2011, 29(6): 120–123.
|
韩玮, 何明. 2015. 外源酶对秸秆堆肥进程的影响及腐熟度模糊评价[J]. 环境科学学报, 2015, 35(11): 3742–3749.
|
李云排, 周维博, 刘雷, 等. 2014. 基于改进可变模糊集的延河水质评价[J]. 人民黄河, 2014, 36(4): 59–64.
|
李文君, 邱林, 陈晓楠, 等. 2011. 基于集对分析与可变模糊集的河流生态健康评价模型[J]. 水利学报, 2011, 42(7): 775–782.
|
李录娟, 邹胜章. 2014. 不同权重确定方法对地下水质量评价的影响研究[J]. 人民长江, 2014, 45(23): 98–102.
DOI:10.3969/j.issn.1001-4179.2014.23.025 |
马玉杰, 郑西来, 李永霞, 等. 2009. 地下水质量模糊综合评判法的改进与应用[J]. 中国矿业大学学报, 2009, 38(5): 745–750.
|
王曼丽, 何江涛, 崔亚丰, 等. 2016. 基于折减系数的地下水污染风险评价方法探究[J]. 环境科学学报, 2016, 36(12): 4510–4519.
|
Wang W, Xu D, Chau K, et al. 2014. Assessment of river water quality based on theory of variable fuzzy sets and fuzzy binary comparison method[J]. Water Resources Management, 28(12): 4183–4200.
DOI:10.1007/s11269-014-0738-4
|
Wang Y K, Sheng D, Wang D, et al. 2014. Variable fuzzy sets theory to assess water quality of the meiliang bay in taihu lake basin[J]. Water Resources Management, 28(3): 867–880.
DOI:10.1007/s11269-014-0521-6
|
薛希龙, 王新民, 胡勇, 等. 2016. 基于FAHP与可变模糊集的矿山生态安全效应评估[J]. 东北大学学报(自然科学版), 2016, 37(1): 94–99.
|
杨伦标, 高英仪, 凌卫新. 2011. 模糊数学原理及其应用[M]. 广州: 华南理工大学出版社.
|
Yan F, Liu L. 2014. Water quality assessment of the li canal using a functional fuzzy synthetic evaluation model[J]. Environmental Science Processes & Impacts, 16(7): 1764–1771.
|
Yan F, Liu L, Zhang Y, et al. 2016. The research of dynamic variable fuzzy set assessment model in water quality evaluation[J]. Water Resources Management, 30(1): 63–78.
DOI:10.1007/s11269-015-1146-0
|
Yang Y, Zhou Z C, Bai Y Y, et al. 2016. Risk assessment of heavy metal pollution in sediments of the fenghe river by the fuzzy synthetic evaluation model and multivariate statistical methods[J]. Pedosphere, 26(3): 326–334.
DOI:10.1016/S1002-0160(15)60046-7
|
张祺, 景朝霞, 刘燚, 等. 2015. 针对正态样本的模糊综合评价法在巢湖水质评价中的应用[J]. 环境工程, 2015, 33(3): 110–112.
|
 2018, Vol. 38
2018, Vol. 38


