2. 广东省环境污染控制与修复技术重点实验室, 广州 510275
2. Guangdong Province Key Laboratory of Environmental Pollution Control and Remediation Technology, Guangzhou 510275
咖啡因是一种消耗量巨大的食品和药品添加剂(Buerge et al., 2003), 进入水环境后, 会对多种水生动植物, 特别是幼体动植物的生长发育产生抑制作用(Moore et al., 2008), 从而影响生态系统.因此, 咖啡因作为环境污染物越来越受到关注(Ellis, 2006; Boxall et al., 2012).前人研究表明, 咖啡因在污水处理厂中的去除率超过90%(Bendz et al., 2005), 但由于输入量大, 其在自然河流中的检出浓度可达到几千ng·L-1, 而且是检出率极高的一种有机物(Dai et al., 2015; Veach et al., 2011; Baker et al., 2011).同时, 咖啡因是一种亲水碱性有机物, 会在自然河流中发生去质子化而带正电, 通常与带负电荷的沉积物颗粒通过离子交换和电化学反应等过程进行吸附, 吸附比例可超过水体初始浓度的70%, 属于易吸附的有机物(Lin et al., 2010).研究发现, 吸附是决定咖啡因在水环境中归趋的重要过程(Zhou et al., 2014; Schaffer et al., 2012; Pan et al., 2009), 会影响咖啡因在水体中的分布、光解和微生物降解等转化过程.
目前, 针对咖啡因吸附行为的实验研究多依据OECD Guideline 106(OECD, 2000)的批实验方法, 为达到较好的吸附效果, 前人研究中咖啡因的初始浓度均达到μg·L-1~mg·L-1级别(Lin et al., 2010; Karnjanapiboonwong et al., 2010; Martínez-Hernández et al., 2016), 远高于自然河流中咖啡因的浓度(通常为ng·L-1级别).同时, 咖啡因的吸附受到多种环境因素的影响, 如pH(Karnjanapiboonwong et al., 2010)、有机质含量(Lin et al., 2010)和水体扰动(Hajj-Mohamad et al., 2017)等, 但已有的研究多停留在单因素层面.传统的批实验方法难以模拟自然河流中水相和固相沉积物界面上发生的咖啡因吸附过程;此外, 自然河流是各种环境因素构成的错综复杂的复合体系, 单因素实验不能反映真实的环境条件, 使得实验室研究与实际测定的吸附结果出现偏差(Zhou et al., 2014).目前, 吸附模型多采用准一级和准二级动力学模型, 也有学者采用线性自由能关系式预测有机物在沉积物有机质上的分配系数fOC, 但上述模型均未考虑环境因素如pH、有机质和温度的作用(Samaraweera et al., 1993; Nguyen et al., 2005; Ho, 2006), 因此, 在实际应用中拟合结果存在较大的误差(Nguyen et al., 2005).为阐明多种环境因素对有机物吸附的影响, 线性方程和神经网络的应用越来越受到重视.例如, Al-Khazrajy等(2016)采用多元线性回归拟合了在不同土壤下5种PPCPs的吸附, 张琛等(2010)和Barron等(2009)则用神经网络分别建立了有机物的吸附预测模型, 且均取得了较好的拟合效果, 但拟合数据仅限于所研究的沉积物样品, 对于不同环境条件的其他研究区域, 模型的拟合效果还有待验证.
综上所述, 目前对咖啡因的吸附行为研究尚不充分, 特别是缺乏模拟水流扰动及多环境因素复合条件下的吸附研究;而可用于自然水体的吸附模型也未建立.因此, 本研究在实验室条件下近似模拟自然河流的水/泥界面, 应用中心复合实验设计(Central Composite Design, CCD)考察4种环境因素(pH、温度、有机质含量和转速)对咖啡因吸附的影响;利用线性方程和神经网络模型对实验数据进行拟合, 并对独立数据进行预测和验证, 通过对比两种模型的拟合度、预测的准确性及稳定性, 建立适用于所考察因素水平内的咖啡因在自然河流沉积物中的吸附预测模型.
2 材料与方法(Materials and methods) 2.1 实验仪器与实验药品沉积物样品:样品采集自石井河的表层(0~5 cm)沉积物, 石井河位于广州市白云区, 干流长19.35 km, 由于接纳上游及沿程的工业废水和生活污水, 河流污染较为严重, 咖啡因浓度最高达到865 ng·L-1 (Yang et al., 2013).研究区域及采样点如图 1所示, 样品经风干后过2 mm筛, 在550 ℃下灼烧1 h以去除有机质及咖啡因, 保存在4 ℃下待用.
 |
| 图 1 研究区域及采样点示意图 Fig. 1 Study area and sampling sites |
实验药品:咖啡因(caffeine, CAF)纯度99.5%(Dr.Ehrenstorfer, Germany), 理化性质如表 1所示;甲醇和乙腈为色谱纯(Merck, Germany);胡敏酸(Humic Acids, HA)购自Aladdin公司(USA).
| 表 1 沉积物物理化学性质 Table 1 Characterization of sediments |
咖啡因储备液:取一定量咖啡因标准品, 用甲醇溶解配成浓度为1 g·L-1的储备液, 于-18 ℃下保存待用.
标准使用液的制备:取一定体积储备液于50 mL容量瓶中, 用0.01 mol·L-1 CaCl2超纯水定容, 加入10 mmol·L-1 NaN3以抑制微生物作用.
实验仪器:三重四极杆液相色谱-质谱联用仪(LC-MS/MS, Thermo Fisher Scientific), 配SPE固相萃取装置(Automatic Science, China), pH计(Mettler Toledo, Swiss)、超纯水仪(Millipore, Germany)、氮吹仪(Anpel Scientific, China).
2.2 实验方法目前, 吸附实验的经典方法是OECD Guideline 106(OECD, 2000), 但该方法将溶液与沉积物样品完全混合, 体现不出自然河流水/沉积物界面的特点, 与真实河流的差异较大;此外, 水槽模拟实验所需仪器复杂庞大, 且不利于进行批量实验.因此, 为在实验室条件下近似模拟自然河流的水/泥界面, 吸附实验在烧杯中进行.在灭菌处理后的250 mL烧杯中平铺20 g沉积物样品, 上覆100 mL咖啡因溶液, 并调节不同的pH、温度、有机质含量、初始浓度和转速等条件, 考察各因素对咖啡因在河流沉积物中吸附的影响.各因素的水平设置根据中心复合实验设计(Central Composite Design, CCD)确定.CCD是响应曲面方法的一种, 其基于数理统计中的多元线性回归分析和最小二乘法原理, 将这两者与实验设计相结合, 提出实验的最优设计法, 该设计组合数量足够多, 取值范围广, 可以全方位优化实验设计, 在尽量少的实验量下全面地了解响应量与输入变量之间的内在关系(Box et al., 1951).在本研究中采用CCD进行实验设计, 有利于探究多种因素与咖啡因吸附比例之间存在的多元关系及可能存在的交互作用.CCD在响应面分析软件Design Expert 8.0.6中进行, 各因素取值范围和大小如表 2所示.实验前, 沉积物样品在121 ℃下高压灭菌15 min以去除微生物作用(Lin et al., 2010; Martínez-Hernández et al., 2014).pH通过0.1 mol·L-1 HCl或0.1 mol·L-1 NaOH调节;由于自然河流沉积物中有机质的成分复杂, 在实验室条件下难以模拟;而有研究表明, 底泥中天然有机质成分以胡敏酸为主(Nguyen, 2000; Stevenson, 1994), 因此, 本实验通过在沉积物样品中添加不同量的胡敏酸, 以模拟不同的有机质含量;设置不同转速的目的是模拟自然条件下不同的水体搅动状况(Gaullier et al., 2017; Hajj-Mohamad et al., 2017), 转速与温度通过水浴恒温振荡器控制;用标准使用液配制不同初始浓度的咖啡因溶液, 实验过程中在所设置时间点取样测定咖啡因浓度.实验以未加沉积物的样品作为对照, 以确定咖啡因的降解和壁吸附现象.
| 表 2 因素的大小及范围 Table 2 Values and ranges of the investigated parameters |
取样后在5000 r·min-1下离心10 min, 取上清液经0.22 μm滤膜过滤, 滤液经固相萃取和氮吹定容后进行LC-MS/MS测定.咖啡因的吸附特性通过吸附比例Kd表示, 可通过式(1)计算.

|
(1) |
式中, Kd为咖啡因的吸附比例, Ce为取样时间点t时对照组中咖啡因浓度(ng·L-1), Ct为取样时间点t时实验组上清液咖啡因浓度(ng·L-1), C0为咖啡因的初始浓度(ng·L-1).
2.3 咖啡因测定采用LC-MS/MS对样品的咖啡因浓度进行测定.流动相为0.1%甲酸水溶液:乙腈(85:15, 体积比), 流速为0.3 mL·min-1, 进样量为2 μL, 咖啡因保留时间为1.55 min.
2.4 吸附模型构建模型的构建分别采用线性回归模型和神经网络模型.线性方程采用多元逐步回归的方法(Arulsudar et al., 2005), 考察因素与有机物吸附之间的线性关系, 各因素对模型的贡献通过F检验确定.由于一些因素与吸附之间可能并非呈线性关系, 如时间与吸附分配系数之间呈对数关系, 且在多因素交互作用下, 单因素与分配系数之间的关系更加难以确定, 因此, 本文尝试应用神经网络模型以解决因素与吸附比例之间的线性与非线性函数关系.反向传播(Back Propagation, BP)神经网络(Volesky, 2003)是一种模仿动物神经网络行为特征进行分布式并行信息处理的算法数学模型, 其优势在于对非线性问题强大的处理能力;输入量从输入层经隐含层逐层计算, 并传向输出层, 如输出层不能得到期望的输出, 则转入误差反向传播过程, 误差信号沿原来的连接通路返回, 逐次调整各层的权值和阀值, 使得误差最小或者达到期望值.神经网络将咖啡因吸附的中间过程黑箱化, 只考虑影响因素和吸附结果的输入-输出映射关系, 适用于解决机理复杂的吸附模拟问题, 但缺点在于无法得出具体的关系式.本研究模型的构建均在Matlab 2014a中完成, 将pH、温度、有机质、初始浓度、转速和时间作为输入量, 吸附比例Kd作为输出量, 得到的神经网络模型结构如图 2所示, 两种模型采用相同的数据分组进行拟合和验证以对比建模效果.实验设置共86组, 有效数据85组, 随机抽取其中9组作为独立验证数据, 另外76组作为拟合数据, 拟合数据与验证数据的比例为90:10;模型可靠性通过拟合值与实测值的相关系数和均方根误差分析.
 |
| 图 2 咖啡因吸附神经网络模型结构 Fig. 2 Structure of neural network for the sorption of caffeine |
各因素对咖啡因吸附的影响如图 3所示, 各图中其他因素浓度均限定为中间值.咖啡因在30 h后吸附比例均超过90%, 此后吸附速率趋于平缓.与此结果相似的是, 多数研究表明有机物的吸附在24 h内即达到吸附平衡(Karickhoff et al., 1979; Pan et al., 2009; Zeng et al., 2006).温度是影响咖啡因吸附的主要因素(图 3a), 随着温度从17.71 ℃升高到27.29 ℃, 咖啡因的吸附比例降低约5%, 可见咖啡因的吸附过程是放热反应.随着转速增大, 水体受到的搅动程度越大, 沉积物的再悬浮也随之增大, 因此, 吸附比例也随着转速的增加而增大(图 3b), 吸附时长为30 h时, 转速从36 r·min-1增大到164 r·min-1, 咖啡因吸附比例从0.92增加到0.98;但增大的幅度随着反应时间的延长而减小;而转速较大时, 咖啡因吸附比例随时间变化幅度也比低转速时小;时间越长、转速越快, 咖啡因的吸附更加饱和.从图 3c可以看出, 温度和转速之间存在较强的交互作用, 在低温条件下, 转速增大对促进咖啡因吸附的程度比高温条件下小.从图 3d可以看出, 在实验前30 h, 沉积物有机质含量的升高对咖啡因吸附有一定的促进作用, 有机质含量从1.81%增加到8.19%, 咖啡因的吸附比例从0.94升高到0.96, 但这种促进作用随着接触时间增长而减弱, 到实验后期4 d, 有机质含量变化的影响很小.pH和初始浓度对咖啡因吸附的影响同样很小(图 3e、3f).
 |
| 图 3 各因素对咖啡因吸附的影响 (a.温度, b.转速, c.转速和温度的交互作用, d.有机质含量, e. pH, f.初始浓度) Fig. 3 Effects of the parameters on the sorption of caffeine (a.temperature, b.rotation speed, c.combined effect of rotation speed and temperature, d.organic content, e.pH, f.initial concentration) |
本研究中咖啡因的吸附比例高于其他研究结果, 如Lin等(2010)的研究中, 咖啡因与底泥接触13 d后仅吸附了76%.不同研究之间的咖啡因吸附程度也存在差异, 如Lin等(2010)研究得到咖啡因的吸附分配系数为250 L·kg-1, Martínez-Hernández等(2014).研究结果为17.86 L·kg-1, Karnjanapiboonwong等(2010)的结果则为0.1 L·kg-1.吸附分配系数越高说明吸附程度越高, 这3篇文献所得的咖啡因吸附分配系数呈1个数量级的递减, 而三者所采用的最高初始浓度分别为6.6、100和4000 μg·L-1, 初始浓度之间则呈现逐级递增, 随着初始浓度的提高, 吸附程度显著下降.这可能是由初始浓度的差异引起的, 由于初始浓度越低, 沉积物吸附点位数量对于低浓度的咖啡因而言相对充足, 咖啡因的吸附比例越高(Martínez-Hernández et al., 2014).而本研究模拟真实河流中咖啡因浓度(小于1000 ng·L-1), 小于一般实验室研究的浓度, 因此, 吸附比例相对于其他研究结果较高.从图 3结果可以看出, 咖啡因在30 h内完成大部分吸附.有研究表明, 有机物吸附的过程可分为液膜扩散、颗粒扩散和吸附反应3个步骤, 而后两者的速率一般相近且远小于液膜扩散(王凯等, 2015).可见, 咖啡因的吸附在30 h内以液膜扩散为主, 之后则主要发生颗粒扩散和吸附反应.温度和转速是影响咖啡因吸附的两个主要因素;温度升高一方面使吸附平衡向逆反应方向移动, 另一方面增大了咖啡因的溶解度, 抑制吸附反应(Zeng et al., 2006);此外, 温度升高在一定程度上促进了咖啡因的解吸, 因此, 温度的升高使吸附比例降低(Cheng et al., 2014).水体的流动会造成搅动使沉积物再悬浮, 增大颗粒与咖啡因之间的接触面积从而促进吸附(王鹏等, 2013);本文通过设置不同的转速以模拟流速变化引起的不同水体搅动状况, 研究结果体现了不同搅动水况下咖啡因吸附的差异.由于本研究中pH均小于咖啡因的pKa(10.4), 咖啡因的去质子化程度都较大, 因此, 离子交换和电化学反应等过程使吸附充分进行, pH的影响较小.
从实验结果可以看出, 咖啡因在沉积物上的吸附容易受到各种环境因素的影响, 因此, 在构建吸附模型时考虑上述因素的影响是必要的.
3.2 线性回归方程线性回归方程拟合为二元一次方程, 具体方程式为:

|
(2) |
式中, Kd为咖啡因吸附比例;A、B、C、D、E和G分别表示pH、有机质含量、温度(℃)、初始浓度(ng·L-1)、转速(r·min-1)和时间(d).
对方程进行方差分析, 结果F值为7.49, 说明该线性方程显著.温度、时间和转速的F值最大, 分别为40.38、38.33和31.58, p值检验结果均小于0.0001, 可见温度在该线性方程模型中显著性最强, 其次是时间和转速;此外, 温度和转速的交互项CE的F值为11.14, 是显著性最强的交互项;但有机质含量、初始浓度和pH的F值仅分别为3.15、1.03和0.069, p值检验结果分别为0.0815、0.3153和0.7945, 均大于0.05, 因此, 在该模型中是不显著项.可见, 各因素的显著性与前文实验结果相符.
如图 4a所示, 对于线性方程拟合数据, 拟合值与实测值的相关性系数为0.8987(p<0.01), 呈显著正相关, 均方根误差为0.022, 信噪比为11.509>4, 说明模型可用于预测.利用所建线性方程对独立验证数据进行预测, 结果如图 4b所示, 对于线性方程验证数据, 拟合值与实测值的相关系数为0.4616(p=0.111).虽然线性方程拟合数据的拟合值与实测值相关性显著, 但验证数据的拟合值总体比实测值偏大, 相关性不显著;从实验结果分析可知, 本研究各因素之间存在一定的交互作用, 在多因素共同作用下, 各参数与吸附比例Kd之间可能存在其他形式的对应关系, 因此, 采用线性回归的方法可能反而带来更大的误差.
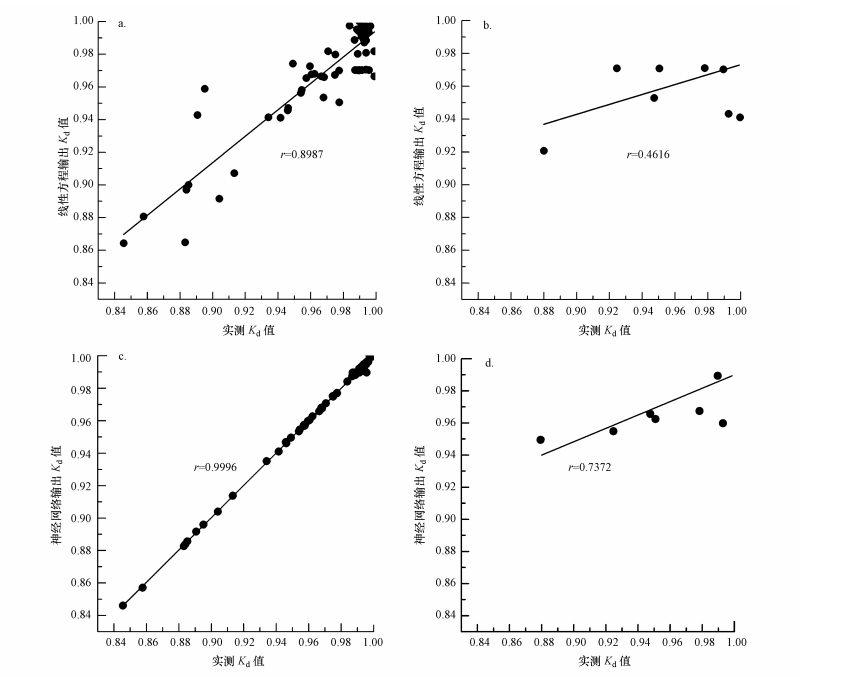 |
| 图 4 模型输出Kd值与实测Kd值的相关分析 (a.线性方程拟合数据, b.线性方程验证数据, c.神经网络拟合数据, d.神经网络验证数据) Fig. 4 Regression of the predicted and actual Kd values of different models (a.training data of linear equation, b.validation data of linear equation, c.training data of neural network, d.validation data of neural network) |
线性方程是近年来被广泛应用的吸附模型.如He等(2006)对五氯酚在不同类型土壤中的吸附与土壤性质进行多元回归分析, 得到在不同土壤中的吸附模型, 其拟合模型的可决系数均在0.8以上;Radka等(2015)同样采用多元回归方法对7种有机物的Freundlich系数进行拟合, 拟合值与实测值的相关系数从0.55到0.97不等, 其中, 甲氧苄氨嘧啶和安替洛尔的相关系数较小, 两者与咖啡因的性质相近, 水溶性强且在天然pH下易电离, 其吸附机理主要是离子交换, 受到的因素影响复杂, 因此, 采用单一的线性关系式拟合效果较差.此外, 前人研究中并未利用独立数据进行模型的验证, 因此, 模型的实际应用效果未知(Al-Khazrajy et al., 2016; Kodešová et al., 2015; He et al., 2006).线性方程虽然能较好地拟合环境因素对咖啡因吸附的影响, 但要达到更高精度的拟合效果, 则需要解决因素与吸附比例之间存在的非线性问题.
3.3 神经网络模型神经网络模型的参数根据Matlab 2014a自带的工具箱确定, 最大训练步数为10000, 学习率为0.001, 目标误差为0.000001, 学习函数采用trainbr函数, 拓扑结构采用3层, 包括1个输入层、1个隐含层和1个输出层;研究表明(Robert, 1988), 3层神经网络能够解决大部分的非线性函数问题.隐含层神经元节点数通过经验公式
模型拟合结果如图 4c、4d所示, 对于神经网络拟合数据, 其拟合值与实测值的相关系数为0.9996(p<0.01), 均方根误差为0.0006;对于神经网络验证数据, 其拟合值和实测值的相关系数为0.7372(p=0.025), 均方根误差为0.0292.神经网络模型拟合和验证数据的拟合值与实测值的相关系数均大于线性方程, 模拟效果较好, 虽然无法得到具体的关系式, 但神经网络对非线性函数优秀的处理能力, 使其对各因素与咖啡因吸附比例之间的映射关系拟合程度较高, 而验证结果也表明神经网络模型有较好的预测能力.
近年来, 越来越多的学者将BP神经网络应用于环境学领域, Barron等(2009)通过对49种PPCPs的批实验和建立神经网络模型, 预测了PPCPs在底泥和污泥上的吸附分配系数Kd, 实验值和模型的预测值的相关系数达到0.88, 表明神经网络在PPCPs吸附上有较好的预测能力.李鱼等(2011)利用BP神经网络建立Cu2+和阿特拉津复合体系中沉积物对阿特拉津吸附量的影响模型, 模型的拟合值和实验值的相关系数达到0.97, 各集合的平均偏差均小于10%.张琛等(2010)构建了沉积物吸附双酚A的BP神经网络模型, 模拟了松花江表层沉积物的不同泥水比、非残渣态组分和双酚A初始浓度对双酚A吸附量的影响, 所建BP神经网络模型的拟合值与实测值的相关系数为0.9665, 并利用遗传算法优化估算了最大吸附量, 优化之后的拟合值与实验值的相对偏差为0.96%~8.21%.上述研究都成功建立了精度较高的神经网络模型, 但均缺少独立验证数据的验证.本研究所建模型基于模拟自然条件的吸附实验数据, 且利用9组独立验证数据进行模型验证, 结果表明了神经网络模型应用于实际预测中的可行性.
3.4 模型稳定性验证由于模型的建模数据和独立验证数据通过随机抽取进行分配, 训练和验证结果容易陷入局部最优化(Arulsudar et al., 2005).因此, 本文采用K折交叉验证(Fielding et al., 1997)对神经网络和线性方程的稳定性进行验证, 将数据集分成K个大小大致相同的子集, 将其中1个子集作为验证集, 另外K-1个子集作为训练集, 进行K次拟合和验证, 联合这K个结果进行泛化误差的估计.K取值一般为2、5和10, 本文对3种取值方法分别进行验证, 交叉验证结果如表 3所示.
| 表 3 模型交叉验证结果 Table 3 Cross validation results of different models |
从交叉验证结果可以看出, 神经网络模型在不同的K取值条件下拟合和验证效果均优于线性方程, 神经网络模型的拟合精度更高、稳定性更好.在不同K值条件下, 神经网络对拟合和验证数据的拟合值与实测值的相关系数平均值均大于线性方程;神经网络对拟合和验证数据的拟合值与实测值的相关系数最大值可达0.9998和0.9923, 而线性方程分别为0.9155和0.9690, 最小值则分别为0.8424和0.3992(神经网络)、0.8314和0.2799(线性方程);可见, 神经网络平均拟合和验证能力都优于线性方程, 且神经网络可以达到更大精度的拟合.神经网络拟合和验证结果的均方根误差均小于线性方程, 说明神经网络模拟结果的离散程度比线性方程小.此外, 比较不同K值验证结果可以看出, 总样本量相同的情况下, 随着拟合数据比例增大, 两种模型对拟合和验证数据的拟合值与实测值的相关系数均减小, 且离散程度有所增大.可见, 不同拟合和验证数据的选取对模型的模拟结果有很大影响, 两者不同的比例选取也会导致不同的模拟结果.但总体而言, 神经网络的拟合效果优于线性方程, 神经网络通过训练可以达到更高的拟合精度且稳定性更好;验证数据的结果也表明应用神经网络的预测效果好于线性方程.
由于线性方程只能拟合因素与咖啡因吸附比例之间的线性关系, 对非线性关系则无法模拟;而神经网络模型能够模拟各因素单独作用和交互作用对咖啡因吸附的影响, 达到更高的拟合精度, 验证结果则进一步确定该模型作为实际预测模型的可行性.本文所建神经网络模型基于实验室模拟的各个因素条件下咖啡因吸附结果, 避免了实验结果的地域性, 在所考虑的因素取值范围内, 该模型具有适用性.
4 结论(Conclusions)本研究在实验室条件下近似模拟了自然河流的水/泥界面, 考察了不同环境因素对咖啡因在沉积物上吸附的影响, 并通过对比不同吸附模型的模拟效果, 得到适用于自然河流的咖啡因吸附神经网络预测模型.实验结果表明, 温度和转速是影响咖啡因吸附的最主要因素, 且两者之间存在交互作用, 而pH、有机质含量和初始浓度的影响较小.吸附比例随着温度的升高而降低, 表明咖啡因的吸附反应是放热过程;随着时间增长、转速增大, 咖啡因的吸附比例随之增大, 但增大的幅度也随着时间和转速的增大而减少.通过对76组实验数据分别进行线性方程和神经网络的拟合, 神经网络对拟合数据的拟合值与实测值的相关系数(0.9996)高于线性方程(0.8987), 神经网络模型拟合程度和精度均优于线性方程.利用模型分别对9组独立验证数据进行预测, 对验证数据的拟合值与实测值的相关系数分别为0.7372和0.4616, 神经网络的预测结果同样好于线性方程.神经网络模型较好地拟合了不同因素与咖啡因吸附比例之间可能存在的线性及非线性关系, 独立验证结果表明, 在所考察的因素取值范围内, 将其应用于预测自然河流中咖啡因在沉积物中的吸附是可行的.本文还应用K折交叉验证对两种模型的稳定性进行检验, 结果表明, 神经网络通过训练可以达到更高的拟合精度且稳定性更好, 具有较强的泛化能力;验证数据的结果也表明神经网络的预测能力优于线性方程.
未来可将神经网络模型与水质模型结合, 用于预测自然河流中咖啡因的迁移过程和时空分布, 评估其对生态系统的影响.此外, 有待探究其他环境因素如离子强度、电导率等的影响, 并通过缩短实验周期、扩大初始浓度范围, 进一步优化神经网络吸附预测模型.
致谢: 中山大学测试中心的姚瑶老师对本研究中咖啡因的测定提供了建议和帮助, 刘广州和徐闯同学在现场采样过程中提供了帮助, 在此一并表示感谢!
Al-Khazrajy O S A, Boxall A. 2016. Impacts of compound properties and sediment characteristics on the sorption behaviour of pharmaceuticals in aquatic systems[J]. Journal of Hazardous Materials, 317: 198–209.
DOI:10.1016/j.jhazmat.2016.05.065
|
Arulsudar N, Subramanian N, Muthy R S. 2005. Comparison of artificial neural network and multiple linear regression in the optimization of formulation parameters of leuprolide acetate loaded liposomes[J]. J Pharm Pharm Sci, 8(2): 243–258.
|
Baker D R, Kasprzyk-Hordern B. 2011. Multi-residue analysis of drugs of abuse in wastewater and surface water by solid-phase extraction and liquid chromatography-positive electrospray ionisation tandem mass spectrometry[J]. Journal of Chromatography A, 1218(12): 1620–1631.
DOI:10.1016/j.chroma.2011.01.060
|
Barron L, Havel J, Purcell M, et al. 2009. Predicting sorption of pharmaceuticals and personal care products onto soil and digested sludge using artificial neural networks[J]. Analyst, 134(4): 663–670.
DOI:10.1039/b817822d
|
Bendz D, Paxéus N A, Ginn T R, et al. 2005. Occurrence and fate of pharmaceutically active compounds in the environment, a case study:Höje River in Sweden[J]. Journal of Hazardous Materials, 122(3): 195–204.
DOI:10.1016/j.jhazmat.2005.03.012
|
Box G E P, Wilson K B. 1951. On the experimental attainment of optimum conditions[J]. Journal of the Royal Statistical Society, 13(1): 1–45.
|
Boxall A, Rudd M A, Brooks B W, et al. 2012. Pharmaceuticals and personal care products in the environment:What are the big questions?[J]. Environmental Health Perspectives, 120(9): 1221–1229.
DOI:10.1289/ehp.1104477
|
Buerge I J, Poiger T, Müller M D, et al. 2003. Caffeine, an anthropogenic marker for wastewater contamination of surface waters[J]. Environmental Science & Technology, 37(4): 691–700.
|
Cheng D, Liu X, Wang L, et al. 2014. Seasonal variation and sediment-water exchange of antibiotics in a shallower large lake in North China[J]. Science of the Total Environment, 476-477: 266–275.
DOI:10.1016/j.scitotenv.2014.01.010
|
Dai G, Wang B, Huang J, et al. 2015. Occurrence and source apportionment of pharmaceuticals and personal care products in the Beiyun River of Beijing, China[J]. Chemosphere, 119: 1033–1039.
DOI:10.1016/j.chemosphere.2014.08.056
|
Ellis J B. 2006. Pharmaceutical and personal care products (PPCPs) in urban receiving waters[J]. Environmental Pollution, 144(1): 184–189.
DOI:10.1016/j.envpol.2005.12.018
|
Fielding A H, Bell J F. 1997. A review of methods for the assessment of prediction errors in conservation presence/absence models[J]. Environmental Conservation, 24(1): 38–49.
DOI:10.1017/S0376892997000088
|
Gaullier C L, Dousset S, Billet D, et al. 2017. Is pesticide sorption by constructed wetland sediments governed by water level and water dynamics?[J]. Environmental Science and Pollution Research.
DOI:10.1007/s11356-017-9123-1
|
Hajj-Mohamad M, Darwano H, Duy S V, et al. 2017. The distribution dynamics and desorption behaviour of mobile pharmaceuticals and caffeine to combined sewer sediments[J]. Water Research, 108: 57–67.
DOI:10.1016/j.watres.2016.10.053
|
He Y, Xu J, Wang H, et al. 2006. Detailed sorption isotherms of pentachlorophenol on soils and its correlation with soil properties[J]. Environmental Research, 101(3): 362–372.
DOI:10.1016/j.envres.2006.01.002
|
Ho Y S. 2006. Review of second-order models for adsorption systems[J]. Journal of Hazardous Materials, 136: 681–689.
DOI:10.1016/j.jhazmat.2005.12.043
|
Karickhoff S W, Brown D S, Scott T A. 1979. Sorption of hydrophobic pollutants on natural sediments[J]. Water Research, 13(3): 241–248.
DOI:10.1016/0043-1354(79)90201-X
|
Karnjanapiboonwong A, Morse A N, Maul J D, et al. 2010. Sorption of estrogens, triclosan, and caffeine in a sandy loam and a silt loam soil[J]. Journal of Soils and Sediments, 10(7): 1300–1307.
DOI:10.1007/s11368-010-0223-5
|
Kodešová R, Grabic R, Kočárek M, et al. 2015. Pharmaceuticals' sorptions relative to properties of thirteen different soils[J]. Science of the Total Environment, 511: 435–443.
DOI:10.1016/j.scitotenv.2014.12.088
|
李鱼, 王倩, 高茜, 等. 2011. 基于BP神经网络的复合污染体系中沉积物吸附阿特拉津的规律[J]. 吉林大学学报(地球科学版), 2011, 41(S1): 315–321.
|
Lin A Y, Lin C, Tung H, et al. 2010. Potential for biodegradation and sorption of acetaminophen, caffeine, propranolol and acebutolol in lab-scale aqueous environments[J]. Journal of Hazardous Materials, 183(1/3): 242–250.
|
Martínez-Hernández V, Meffe R, Herrera López S, et al. 2016. The role of sorption and biodegradation in the removal of acetaminophen, carbamazepine, caffeine, naproxen and sulfamethoxazole during soil contact:A kinetics study[J]. Science of the Total Environment, 559: 232–241.
DOI:10.1016/j.scitotenv.2016.03.131
|
Martínez-Hernández V, Meffe R, Herrera S, et al. 2014. Sorption/desorption of non-hydrophobic and ionisable pharmaceutical and personal care products from reclaimed water onto/from a natural sediment[J]. Science of the Total Environment, 472: 273–281.
DOI:10.1016/j.scitotenv.2013.11.036
|
Moore M T, Greenway S L, Farris J L, et al. 2008. Assessing caffeine as an emerging environmental concern using conventional approaches[J]. Archives of Environmental Contamination and Toxicology, 54(1): 31–35.
DOI:10.1007/s00244-007-9059-4
|
Nguyen L M. 2000. Organic matter composition, microbial biomass and microbial activity in gravel-bed constructed wetlands treating farm dairy wastewaters[J]. Ecological Engineering, 16(2): 199–221.
DOI:10.1016/S0925-8574(00)00044-6
|
Nguyen T H, Goss K, Ball W P. 2005. Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments[J]. Environmental Science & Technology, 39(4): 913–924.
|
OECD. 2000. Adsorption-Desorption Using a Batch Equilibrium Method//OECD Guideline for the Testing of Chemicals[M]. Paris: Organization for Economic Cooperation and Development
|
Pan B, Ning P, Xing B. 2009. Part V-sorption of pharmaceuticals and personal care products[J]. Environmental Science and Pollution Research, 16(1): 106–116.
DOI:10.1007/s11356-008-0052-x
|
Hecht-Nielsen R. 1988. Theory of the backpropagation neural network[J]. Neural Networks, 1(S1): 593–605.
|
Samaraweera M, Jolin W, Vasudevan D, et al. 1993. Atomistic prediction of sorption free energies of cationic aromatic amines on montmorillonite:A linear interaction energy method[J]. Rapid Communications in Mass Spectrometry, 7(7): 163–166.
|
Schaffer M, Boxberger N, Börnick H, et al. 2012. Sorption influenced transport of ionizable pharmaceuticals onto a natural sandy aquifer sediment at different pH[J]. Chemosphere, 87(5): 513–520.
DOI:10.1016/j.chemosphere.2011.12.053
|
Stevenson F J. 1994. Humus chemistry:genesis, composition, reactions[J]. Soil Science, 135(2): 129–130.
|
Veach A M, Bernot M J. 2011. Temporal variation of pharmaceuticals in an urban and agriculturally influenced stream[J]. Science of the Total Environment, 409(21): 4553–4563.
DOI:10.1016/j.scitotenv.2011.07.022
|
Volesky B. 2003. Biosorption process simulation tools[J]. Hydrometallurgy, 71(1/2): 179–190.
|
王凯, 李侃竹, 周亦圆, 等. 2015. 河流沉积物对典型PPCPs的吸附特性及其影响因素[J]. 环境科学, 2015, 36(3): 847–854.
|
王鹏, 冯燕, 蔡赟杰. 2013. 水动力条件对太湖底泥吸附苯胺性能的影响[J]. 环境科学与技术, 2013, 36(5): 117–123.
|
Yang X, Chen F, Meng F, et al. 2013. Occurrence and fate of PPCPs and correlations with water quality parameters in urban riverine waters of the Pearl River Delta, South China[J]. Environmental Science and Pollution Research, 20(8): 5864–5875.
DOI:10.1007/s11356-013-1641-x
|
Zeng G, Zhang C, Huang G, et al. 2006. Adsorption behavior of bisphenol A on sediments in Xiangjiang River, Central-south China[J]. Chemosphere, 65(9): 1490–1499.
DOI:10.1016/j.chemosphere.2006.04.013
|
张琛, 刘建林, 胡艳, 等. 2010. BP神经网络模型在表层沉积物及其非残渣态组分吸附双酚A研究中的应用[J]. 地理科学, 2010, 30(3): 435–440.
|
Zhou J, Broodbank N. 2014. Sediment-water interactions of pharmaceutical residues in the river environment[J]. Water Research, 48: 61–70.
DOI:10.1016/j.watres.2013.09.026
|
 2018, Vol. 38
2018, Vol. 38


