2. 中国海洋大学经济学院, 青岛 266100
2. School of Economy, Ocean University of China, Qingdao 266100
随着全球气候变化问题的不断加重, 各国共同面临降低二氧化碳排放量的压力.而能源活动作为二氧化碳排放量的主要来源, 那些由于能源的高投入和高消耗引起的经济增长必然会导致二氧化碳排放量的增加.理解经济增长与二氧化碳排放量之间的关系是各国制定碳减排策略的重要问题.进入后京都时代, 不论是发达国家还是发展中国家, 均采取更加灵活和务实的态度去应对巨大的减排压力.许多国家将碳排放强度作为约束性指标纳入到国民经济和社会发展中长期规划中, 通过碳排放总量控制来平衡国民经济增长与碳减排要求.因此, 亟需一种能够准确预测二氧化碳排放总量的方法, 为减少二氧化碳排放量以应对全球气候变暖问题提供理论依据和指引.
二氧化碳排放量预测作为碳排放总量控制的核心问题之一, 在学术研究和实践操作两方面均取得了较好的成绩.本文以预测方法为脉络对现有文献进行总结和分析.一些学者运用1个或多个二氧化碳排放量的影响因素分析二氧化碳排放量的变化趋势并对其进行预测, 这类模型主要包括面板模型、EKC模型、STIRPAT模型和多元神经网络模型.Schmalensee等(1998)运用随机效应面板模型对1990-2050期间世界整体的碳排放量水平进行预测.Galeotti & Lanza(1999)运用110个国家的面板数据研究二氧化碳排放量与GDP之间的关系, 并用EKC模型对2000-2020年期间二氧化碳排放量进行预测.STIRPAT模型是分析碳排放影响因素及其变动趋势的主要方法, 目前渠慎宁和郭朝先(2010)、Wang等(2012)、杜强等(2012)、王宪恩等(2014)、黄蕊等(2016)运用该模型分析碳排放的影响因素已比较全面, 但是每个学者选取的影响因素不尽相同, 从而对碳排放的变动趋势具有不同的预期.Behrang等(2011)运用人工神经网络研究人口、GDP、石油贸易和天然气贸易与二氧化碳排放量之间的关系, 并预测世界二氧化碳排放量水平.
一些学者仅运用二氧化碳排放量自身的时间序列数据研究分析其变化趋势并对其进行预测, 该类模型主要包括灰色预测模型、DDEPM模型、Logistic模型.灰色预测模型在数据较少的情况下可以实现对碳排放量较为精准的预测, Pao & Tsai(2011)、Lin等(2011)、张乐勤等(2012)均运用灰色预测模型对碳排放量问题进行研究.Lee & Tong(2011)运用遗传算法对灰色模型的误差进行修正, 基于改进的灰色模型GPGM(1, 1)对中国能源消费进行预测.Pao等(2012)运用数字迭代法最优化非线性灰色伯努利模型参数, 构建NGBM-OP模型预测中国二氧化碳、能源消费和实际产出值.DDEPM模型适用于上下波动的时间序列, 刘广为等(2012)、赵息等(2013)认为该模型对碳排放数据的预测具有较高的精度.Logistic模型可以较好的描述S形曲线的特征, 杜强等(2013)、丁胜等(2014)基于Logistic模型实现碳排放的动态预测.
通过对现有文献的梳理, 发现存在以下不足:第一, 考虑二氧化碳排放量影响因素的一类模型一般通过加总方式将高频数据变为低频数据, 从而满足模型两侧变量必须是同频率的要求.但这样处理降低了部分高频数据携带的有效信息.并且该类模型对二氧化碳排放量的预测是基于对相关影响因素的预测或情境设置实现的, 这在一定程度上降低了该类模型对二氧化碳排放量的预测精度.第二, 只运用二氧化碳排放量自身时间序列的一类模型虽然不存在模型两边必须同频率的限制, 但是该类模型只关注二氧化碳排放量自身的变化规律, 而忽视其他相关因素对二氧化碳排放量的影响, 也在一定程度上降低该类模型对二氧化碳排放量的预测精度.第三, 二氧化碳排放行为具有典型路径依赖性特征, 但以往研究很少同时考虑二氧化碳排放量自身及影响因素的滞后效应, 这也在一定程度上降低了二氧化碳排放量的预测精度.
本文基于现有研究的不足, 采用混频数据抽样模型(MIDAS)对碳排放量预测问题进行了研究.基于高频数据GDP进行了二氧化碳排放量的预测, 并与OLS、PDL、ADL、AR、MA、ARMA基准模型的预测精度进行比较分析, 为各国碳排放总量控制策略的实施提供预测分析的理论与技术基础.本文的创新之处主要体现在3个方面:第一, 将MIDAS模型引入二氧化碳排放量预测领域, 直接利用高频GDP数据预测低频二氧化碳排放量, 充分利用高频数据携带的有效信息;第二, 本研究可以实现运用历史GDP数据对未来二氧化碳排放量的预测, 而不是依赖于对未来期高频GDP的预测或情景设定, 并且运用最新公布的季度GDP数据对二氧化碳排放量预测值不断修正从而实现二氧化碳排放量的实时报道;第三, 本研究在预测过程中同时考虑二氧化碳排放量自身的滞后效应以及GDP与二氧化碳排放量之间的动态效应.
2 研究方法与数据来源(Method and data sources) 2.1 MIDAS模型构建混频数据抽样模型(MIDAS)由Ghysels等(2004)提出, 该模型源于分布滞后模型的思想, 通过多项式权重函数实现直接利用高频数据对低频数据进行解释和预测.根据现有学者的研究, 目前共有Beta权重函数、BetaNN权重函数、阿尔蒙指数权重函数、阿尔蒙权重函数、分段函数和非限制性权重函数6种多项式权重形式.本文将通过比较分析6种权重形式下MIDAS模型的预测精度, 选取最优的多项式权重形式.
2.1.1 单变量MIDAS模型单变量MIDAS模型只考虑一种解释变量对被解释变量的影响, 研究两者之间的动态关系.年度二氧化碳增长率为growthCO2, t, 季度GDP增长率为growthGDP, t(m), 季度GDP在[t-1,t]年度内可以观测到m个数值, 即m是高频率数据和低频率数据的频率倍差.在本文中, m=4.二氧化碳排放量预测的MIDAS模型可以表示为:

|
(1) |
式中, α为常数项, β为系数, εt为模型误差项;growthCO2, t指t时期二氧化碳排放量增长率;growthGDP, t(m)指t时期GDP增长率;W(L1/m, θ)是多项式权重, 
向前h步的混频数据抽样模型(MIDAS(m, K, h))与基础混频数据抽样模型和传统的同频预测模型相比, 该模型具有可以对年度数据实时预报和修正的优点.一般来说, 传统的同频预测模型在预测年度数据时, 使用的都是年度数据, 而实时年度数据的获取具有一定的时滞性, MIDAS(m, K, h)可以充分利用已更新的季度数据来对年度数据进行实时预测, 并不断更新和修正预测的结果.当h=1, 即向前1步混频数据抽样模型, 用第t年前3季度及之前的数据来预测第t年的年度数据.当h=4时, 即可以用t-1年度及之前的季度数据对t年年度数据进行预测.假设目前季度GDP更新到t年的第3季度, 则向前1步混频数据抽样模型(h=1)可以实现对t年度二氧化碳排放量进行预测, 向前5步混频数据抽样模型(h=5)可以实现对t+1年度二氧化碳排放量进行预测.
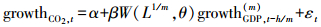
|
(2) |
式中, m是高频率数据和低频率数据的频率倍差;W(L1/m, θ)是多项式权重, L1/m滞后因子.
自回归单变量混频数据抽样模型(AR(P)-MIDAS(m, K))在基础混频数据抽样模型的基础上考虑之前期二氧化碳排放量对当期二氧化碳排放量的影响, 即考虑了二氧化碳排放量自身之间的动态效应.其模型表达式可以示为如下形式:
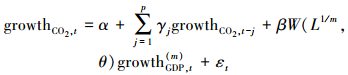
|
(3) |
式中, j表示二氧化碳排放量的滞后阶数, p为其最大滞后阶数;γj为二氧化碳排放量各滞后期对当期的影响效应.
2.1.2 多项式权重的选取多项式权重可以有效减少模型的待估参数, 本文共讨论6种多项式权重对混频数据抽样模型预测精度的影响, 并从中选出最优的多项式权重形式.贝塔密度函数(Beta)的形式为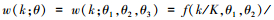
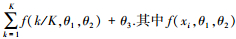
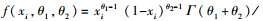
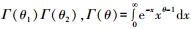
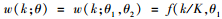


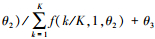
阿尔蒙指数权重函数(Exp Almon)具有使方程获得零逼近误差的性质, 是目前最常使用的一种权重形式, 其表达形式如下: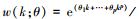
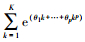
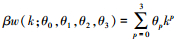
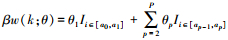
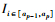
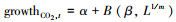

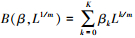
GDP反映一国经济增长的整体水平, 以能源的高投入、高消耗带来的经济增长势必会导致二氧化碳排放量的增加.经济增长与二氧化碳排放量之间到底存在着什么样的关系是国家在制定减排措施时面临的一个重要问题.基于此, 本文选取季度GDP为解释变量, 研究季度GDP与二氧化碳排放量之间的动态关系并实现二氧化碳排放量的实时预测.
由于数据的可得性和完整性, 本文选取1971-2015年中国二氧化碳排放量和季度GDP(当季值)为样本,研究MIDAS模型在二氧化碳排放量预测方面的适用性.由于中国自1992年才开始公布季度GDP数据, 因此本文利用Eviews8.0按照二次匹配总和原则(Quadratic-match sum)把1992年之前的年度GDP数据转化为季度GDP数据进行研究.数据皆来自于Wind数据库.年度二氧化碳排放量、GDP与季度GDP的变化趋势如图 1所示.由图 1可看出季度GDP仍具有年度GDP的变化趋势, 说明经过频率转化后的季度GDP较好地保留了原有数据的特征.在1971-2015研究样本期间, 二氧化碳与GDP在2001年前增长速度较为缓慢, 但在2001年后均具有较高的增速, 呈现出明显的分段特征.二氧化碳排放量由1971年的882.257×106 t到2015年增加为9153.897×106 t, 二氧化碳排放量于2014和2015年两年增加速度减缓, 基本维持不变.季度GDP由1971年第一季度的600.804亿元增加到2015年第四季度的192851.9亿元, 并一直处于上升的趋势.整体上, 二氧化碳与GDP在研究样本区间内具有相似的变化趋势.
 |
| 图 1 二氧化碳与GDP变化趋势图 Fig. 1 Change trends of carbon dioxide emissions and GDP |
在下文的实证分析中, 为了消除数据的异方差性, 本文以季度GDP和年度二氧化碳排放量的增长率为研究对象, 其计算公式如式(6)所示:
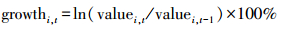
|
(6) |
式中, growthi, t表示指标i在t时期的增长率, i在本文中指季度GDP和年度二氧化碳排放量.
3 结果及分析(Results and analysis) 3.1 MIDAS模型预测结果分析本文首先根据MIDAS模型的样本外预测精度确定出季度GDP和二氧化碳排放量的最优滞后阶数和最优参数估计.本文以1971年至2010年二氧化碳排放量和相应的季度GDP数据为模型的估计样本, 在此基础上对2011年至2015年的二氧化碳排放量进行样本外预测.在分析过程中, 本文以均方根误差(RMSE: Root Mean Square Error)指标作为衡量模型优劣的依据, 因为RMSE指标可以较好的反映模型的预测精度.RMSE越小意味着模型的预测精度越高.
在下文的分析中, 为了充分反映RMSE随变量滞后阶数变化所呈现的变化趋势, 经过试验调整, 最终确定高频GDP的滞后阶数由1阶变化至12阶, 低频二氧化碳排放量的滞后阶数由0阶变化至5阶, 以确定季度GDP与年度二氧化碳排放量的最优滞后阶数.本文利用6种参数权重形式和不同的二氧化碳排放量与GDP滞后阶数构建不同的混频数据抽样模型.在进行参数估计时, 本文以均方根误差RMSE最小原则确定最优权重函数形式及高频GDP和低频二氧化碳排放量的最优滞后阶数.各混频数据模型的样本外预测精度如表 1所示.
| 表 1 不同混频模型RMSE值 Table 1 RMSE of different MIDAS models |
由于篇幅的限制, 本文只列出一些具有代表性滞后阶数的混频数据抽样模型的预测精度.混频数据抽样模型随着高频GDP滞后阶数的变动, 其样本外预测精度也在不断变化.由表 1可以看出当二氧化碳排放量的滞后阶数为0时, 季度GDP最优滞后阶数为5且最优多项式权重形式为UMIDAS, 其预测精度为2.846.当二氧化碳排放量的滞后阶数为1时, 季度GDP最优滞后阶数为6且最优多项式权重形式仍为UMIDAS, 其预测精度为2.152.当二氧化碳排放量的滞后阶数为2时, 季度GDP最优滞后阶数仍为6且最优多项式权重形式依然为UMIDAS, 其预测精度为2.157.当二氧化碳排放量的滞后阶数为3时, 季度GDP最优滞后阶数仍然为6且最优多项式权重形式为UMIDAS, 其预测精度为1.960.当二氧化碳排放量的滞后阶数为4时, 季度GDP最优滞后阶数仍然为6且最优多项式权重形式依然为UMIDAS, 其预测精度为1.703.当二氧化碳排放量的滞后阶数为5时, 季度GDP最优滞后阶数为7且最优多项式权重形式为Almon, 其预测精度为1.978.随着二氧化碳滞后阶数由0变至5, 具有最高预测精度的季度GDP滞后阶数为5至7个季度, 意味着季度GDP对二氧化碳排放量的影响持续时间较短, 该影响一般维持在2年以内.通过对比可知, 当二氧化碳滞后阶数为4、季度GDP滞后阶数为6时, 自回归非限制性混频数据抽样模型(AR(4)-UMIDAS(4, 6))对2011-2015年期间的二氧化碳排放量的预测具有较高的精度.该模型中各个滞后期的季度GDP的权重变化如图 2所示.由该图所示的权重变化趋势可以看出季度GDP对二氧化碳排放量的影响在(-1, 2)之间变化, 且具有正负两种效应.
 |
| 图 2 AR(4)-UMIDAS (4, 6)模型权重变化趋势图 Fig. 2 Change trend of weights of AR(4)-UMIDAS(4, 6) |
AR(4)-UMIDAS(4, K)模型在不同GDP滞后阶数下的多项式权重和均方根误差RMSE分别如图 3a和3b所示.
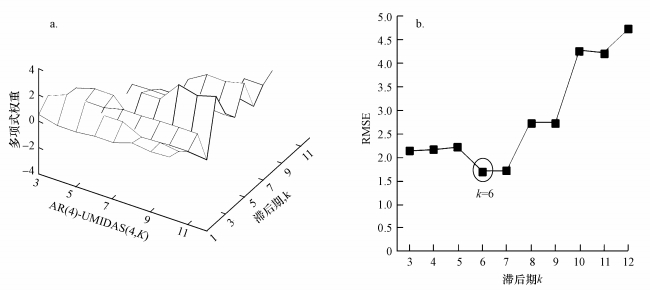 |
| 图 3 AR(4)-UMIDAS (4, K)模型多项式权重(a)和RMSE变化趋势图(b) Fig. 3 Change trends of polynomial weights (a) and RMSE (b) of AR(4)-UMIDAS(4, K) |
通过对上述各种混频数据抽样模型进行比较确定出AR(4)-UMIDAS(4, 6)模型对二氧化碳排放量的样本外拟合精度具有比较优势, 该模型的参数估计结果见表 2.估计结果表明二氧化碳排放量会受自身4年内变化的影响, 二氧化碳排放量自身的总影响效应为57.5%, 其中二氧化碳排放量滞后一期对当期二氧化碳排放量的影响效应最大, 其影响程度为58%.二氧化碳这种影响方向和影响程度与我国实际经济运行情况相吻合.季度GDP对二氧化碳排量具有正负两种效应, 该效应会持续6个季度且以正效应为主, 其对二氧化碳排放量的延迟总乘数效应高达91.2%.可见GDP的增加是引起二氧化碳排放量增加的主要原因.这主要是因为能源活动对二氧化碳排放量的影响具有主导作用, 一国的经济增长方式具有路径依赖性, 其在短期内是很难发生大幅度变化的, 并且这种惯性在经济发展过程中是普遍存在的.季度GDP延迟1阶对二氧化碳排放量的影响效应为0.163, 延迟2阶的影响效应高达1.860, 这说明第三季度GDP对本年度二氧化碳排放量的增加具有的效应最为明显, 是本年度二氧化碳排放量高速增加的时期.
| 表 2 AR(4)-UMIDAS(4, 6)模型参数估计结果 Table 2 Estimation results of AR(4)-UMIDAS(4, 6) |
基准模型是用来比较分析本文所构建的AR(4)-UMIDAS(4, 6)模型预测优劣的一些简单的宏观经济预测模型, 本文主要采用OLS、PDL、ADL、AR、MA、ARMA这6种模型作为基准模型.基准模型在预测的过程中均采用同频率的低频数据, 本文运用1971-2015年期间年度二氧化碳排放量与GDP数据作为基准模型的研究样本.与AR(4)-UMIDAS(4, 6)模型一致, 基准模型均采用1971-2010年样本区间对模型进行估计, 并对2011-2015年样本期间的二氧化碳排放量进行预测.本文通过AR(4)-UMIDAS(4, 6)模型与基准模型的预测精度(RMSE)的比值对其进行优劣性比较.如rRMSEb表示AR(4)-UMIDAS(4, 6)模型与相应的基准模型的RMSE的比值, 在本文中b分别代表OLS、PDL、ADL、AR、MA、ARMA这6种基准模型.若rRMSEb值小于1, 则说明AR(4)-UMIDAS(4, 6)模型的RMSE值小于相应的基准模型, 即AR(4)-UMIDAS(4, 6)模型的预测精度要优于相应的基准模型.6种基准模型对2011-2015年期间二氧化碳排放量预测的RMSE值及AR(4)-UMIDAS(4, 6)模型与基准模型的RMSE比值如下表 3所示.在6种基准模型中, AR模型对二氧化碳排放量的预测精度最高, 其RMSE值为2.071.AR(4)-UMIDAS(4, 6)模型的RMSE值要小于基准模型的RMSE值, 即AR(4)-UMIDAS(4, 6)模型与基准模型相比, 其对二氧化碳排放量的预测精度有了较大的提升.该模型相比较于AR模型, 预测精度提升了18%左右, 但是该模型相对于MA模型, 其预测精度的提升高达70%左右.
| 表 3 AR(4)-UMIDAS(4, 6)模型与基准模型对比分析表 Table 3 Comparison analysis among AR(4)-UMIDAS(4, 6) and benchmark models 0.634 |
在上文分析的基础上, 本文构建的AR(4)-UMIDAS(4, 6)模型对2011-2015年期间二氧化碳排放量的样本外预测精度具有比较优势.因此, 本文在AR(4)-UMIDAS(4, 6)模型的基础上构建向前h步MIDAS模型AR(4)-UMIDAS(4, 6, h), 该模型不仅可以进行样本外预测, 而且还可以及时运用最新公布的季度GDP数据对二氧化碳排放量进行实时报道, 并对二氧化碳排放量的预测不断进行更新和修正.本文选择1971-2015年全样本区间作为AR(4)-UMIDAS(4, 6, h)模型的估计样本, 对AR(4)-UMIDAS(4, 6, h)模型与6种基准模型的样本内预测精度进行比较.AR(4)-UMIDAS(4, 6, h)模型在不同向前步数情况下的多项式权重和RMSE值变化趋势分别如图 4a和4b所示.当h=0与h=1时, 即AR(4)-UMIDAS(4, 6)模型与AR(4)-UMIDAS(4, 6, 1)模型的预测精度较好.这意味着在进行二氧化碳排放量预测时, 运用最新的GDP数据会提高模型的预测精度, 并且二氧化碳排放量主要受近期季度GDP的影响, 随着时间的向前推移, 季度GDP对二氧化碳排放量的影响逐渐下降.
 |
| 图 4 AR(4)-UMIDAS (4, 6, h)模型多项式权重(a)和RMSE变化趋势(b)图 Fig. 4 Change trends of polynomial weights (a) and RMSE (b) of AR(4)-UMIDAS(4, 6, h) |
AR(4)-UMIDAS(4, 6, h)模型与基准模型对1971-2015年期间二氧化碳排放量的样本内预测的RMSE比值如表 4所示.其中rRMSEOLS表示AR(4)-UMIDAS(4, 6, h)模型与基准模型OLS的RMSE比值, 以下类同.对于ADL基准模型, 当h较小时, AR(4)-UMIDAS(4, 6, h)模型的预测精度具有比较优势.因此, 当h≤1时, AR(4)-UMIDAS(4, 6, h)模型对二氧化碳排放量的预测精度仍然高于ADL基准模型的预测精度, 当h≥2时, 存在AR(4)-UMIDAS(4, 6, h)模型对二氧化碳排放量的预测精度略低于ADL基准模型的预测精度的情况.这说明本年度第四季度和第三季度的GDP对当年度二氧化碳排放量的影响占主导地位, 仅仅利用第三季度之前的GDP对当年度二氧化碳排放量进行预测, 其预测效果会下降.因此, AR(4)-UMIDAS(4, 6, h)模型适合对二氧化碳排放量进行短期预测.对于OLS、PDL、AR、MA与ARMA 5种基准模型, AR(4)-UMIDAS(4, 6, h)模型的预测精度具有较大幅度的提高, 这意味着AR(4)-UMIDAS(4, 6, h)模型对于未来3年内二氧化碳排放量的预测仍具有较大的参考价值.
| 表 4 AR(4)-UMIDAS(4, 6, h)模型与基准模型对比分析表 Table 4 Comparison analysis among AR(4)-UMIDAS(4, 6, h) and benchmark models |
基于上文的分析, 本文运用AR(4)-UMIDAS(4, 6, h)模型在1971-2015年全样本期间的估计结果对2016年二氧化碳排放量进行实时预报和短期预测, 并对2017年和2018年的二氧化碳排放量进行预测, 其结果如表 5所示.表 5选取滞后6阶的季度GDP, 向前0~12步的非限制性混频数据抽样模型, 运用最新公布的2016年第四季度GDP数据对二氧化碳排放量进行实时预测.预测结果显示在2016-2018年期间我国二氧化碳排放量将维持一个较低的增长率水平.以AR(4)-UMIDAS(4, 6, 1)模型的预测结果为例, 该预测结果显示2016年我国二氧化碳排放量的增长率为-0.254%, 即2016年我国二氧化碳排放量预测值为9130.675×106 t.AR(4)-UMIDAS(4, 6, 4)模型预测我国2017年二氧化碳排放量的增长率为2.545%, 即我国2017年二氧化碳排放量的预测值为9366.014×106 t.AR(4)-UMIDAS(4, 6, 8)模型预测我国2018年二氧化碳排放量的增长率为4.228%, 即我国2018年二氧化碳排放量的预测值为9770.461×106 t.由于AR(4)-UMIDAS(4, 6, h)模型在短期内具有预测优势, 因此本文认为表 5中的估计结果应以具有较小向前步数的AR(4)-UMIDAS(4, 6, h)模型的预测结果为主, 并把具有较大向前步数的AR(4)-UMIDAS(4, 6, h)模型的预测结果作为参考, 并在最新季度GDP数据公布后, 利用AR(4)-UMIDAS(4, 6, h)模型对其预测结果进行修正和调整.
| 表 5 AR(4)-UMIDAS(4, 6, h)模型预测结果 Table 5 Forecasting of AR(4)-UMIDAS(4, 6, h) |
本文构建混频数据抽样模型(MIDAS), 运用1971-2015年样本期间年度二氧化碳排放量与季度GDP数据研究季度GDP与二氧化碳排放量之间的动态效应并对二氧化碳排放量进行预测.本文选取1971-2010年样本期间的二氧化碳排放量数据和相应的季度GDP数据对模型进行估计, 并对2011-2015年样本期间的二氧化碳排放量进行样本外预测, 通过比较不同混频数据抽样模型的样本外预测精度, 确定在不同混频数据抽样模型中, 自回归非限制性混频数据抽样模型(AR(4)-UMIDAS(4, 6))的预测精度具有比较优势且优于OLS、PDL、ADL、AR、MA、ARMA 6种基准模型.在此基础上构建向前h步自回归非限制性混频数据抽样模型(AR(4)-UMIDAS(4, 6, h))利用最新公布的季度GDP数据对二氧化碳排放量进行实时预测和修正.综合以上分析, 本文主要得出以下结论:
1) 混频数据抽样模型的最优估计结果显示高频季度GDP每一滞后期均具有较高的估计系数, 这表明混频数据抽样模型可以充分利用高频季度GDP数据携带的有效信息.高频季度GDP的引入, 使二氧化碳排放量的预测精度有了较大幅度的提升.与基准模型相比, 该模型具有明显的比较优势.
2) 高频季度GDP对年度二氧化碳排放量的样本外预测结果显示, 我国高频季度GDP对二氧化碳排放量具有较强的解释能力, 其对二氧化碳排放量具有正负两种效应, 该效应会持续6个季度且以正效应为主.二氧化碳排放量自身之间也存在着相互影响, 这种影响会持续4年之久.该结论与我国的经济运行状况相吻合.
3) 混频数据抽样模型利用最新公布的2016年第四季度GDP数据对2016二氧化碳排放量进行实时报道并对2017和2018年二氧化碳排放量进行预测, 结果显示在2016-2018年期间, 我国二氧化碳排放量增长缓慢, 将维持一个较低的增长率水平, 意味着我国碳减排措施成果显著.
4) 二氧化碳排放量的影响因素有很多, GDP并不是影响二氧化碳排放量的唯一因素.所以未来的研究集中于构建适用于二氧化碳排放量预测的多元混频数据抽样模型, 使其预测具有更高的精度.
Behrang M A, Assareh E, Assari M R, et al. 2011. Using bees algorithm and artificial neural network to forecast world carbon dioxide emission[J]. Energy Sources, Part A:Recovery, Utilization, and Environmental Effects, 33(19): 1747–1759.
DOI:10.1080/15567036.2010.493920
|
杜强, 陈乔, 杨锐. 2013. 基于Logistic模型的中国各省碳排放预测[J]. 长江流域资源与环境, 2013(2): 143–151.
|
丁胜, 温作民, 彭玲. 2014. 基于Logistic模型的江苏林业产业碳排放研究[J]. 生态经济, 2014(10): 73–76.
DOI:10.3969/j.issn.1671-4407.2014.10.017 |
Galeotti M, Lanza A. 1999. Richer and cleaner? A study on carbon dioxide emissions in developing countries[J]. Energy Policy, 27(10): 565–573.
DOI:10.1016/S0301-4215(99)00047-6
|
Ghysels E, Santa-Clara P, Valkanov R. 2004. The MIDAS touch:Mixed data sampling regression models[J]. Finance.
|
黄蕊, 王铮, 丁冠群, 等. 2016. 基于STIRPAT模型的江苏省能源消费碳排放影响因素分析及趋势预测[J]. 地理研究, 2016(4): 781–789.
|
Lin C S, Liou F M, Huang C P. 2011. Grey forecasting model for CO2 emissions:A Taiwan study[J]. Applied Energy, 88(11): 3816–3820.
DOI:10.1016/j.apenergy.2011.05.013
|
Lee Y S, Tong L I. 2011. Forecasting energy consumption using a grey model improved by incorporating genetic programming[J]. Energy Conversion and Management, 52(1): 147–152.
DOI:10.1016/j.enconman.2010.06.053
|
刘广为, 赵涛, 米国芳. 2012. 中国碳排放强度预测与煤炭能源比重检验分析[J]. 资源科学, 2012(4): 677–687.
|
Pao H T, Fu H C, Tseng C L. 2012. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model[J]. Energy, 40(1): 400–409.
DOI:10.1016/j.energy.2012.01.037
|
Pao H T, Tsai C M. 2011. Modeling and forecasting the CO2 emissions, energy consumption, and economic growth in Brazil[J]. Energy, 36(5): 2450–2458.
DOI:10.1016/j.energy.2011.01.032
|
渠慎宁, 郭朝先. 2010. 基于STIRPAT模型的中国碳排放峰值预测研究[J]. 中国人口.资源与环境, 2010, 20(12): 10–15.
|
Schmalensee R, Stoker T M, Judson R A. 1998. World carbon dioxide emissions:1950-2050[J]. Review of Economics and Statistics, 80(1): 15–27.
DOI:10.1162/003465398557294
|
Wang Z, Yin F, Zhang Y, et al. 2012. An empirical research on the influencing factors of regional CO2 emissions:evidence from Beijing city, China[J]. Applied Energy, 100: 277–284.
DOI:10.1016/j.apenergy.2012.05.038
|
杜强, 陈乔, 陆宁. 2012. 基于改进IPAT模型的中国未来碳排放预测[J]. 环境科学学报, 2012, 32(09): 2294–2302.
|
王宪恩, 王泳璇, 段海燕. 2014. 区域能源消费碳排放峰值预测及可控性研究[J]. 中国人口.资源与环境, 2014(8): 9–16.
|
张乐勤, 李荣富, 陈素平, 等. 2012. 安徽省1995-2009年能源消费碳排放驱动因子分析及趋势预测——基于STIRPAT模型[J]. 资源科学, 2012(2): 316–327.
|
赵息, 齐建民, 刘广为. 2013. 基于离散二阶差分算法的中国碳排放预测[J]. 干旱区资源与环境, 2013(1): 63–69.
|
 2018, Vol. 38
2018, Vol. 38


