2. 湖南师范大学地理空间大数据挖掘与应用湖南省重点实验室, 长沙 410081
2. Key Laboratory of Geospatial Big Data Mining and Application, Hunan Province, Changsha 410081
稳定同位素大气水平衡模式(isotope Atmospheric Water Balance Model, 记作iAWBM)是一个全球的网格点模式.在该模式中, 水稳定同位素的平衡方程包括大气水汽中的稳定同位素、水汽稳定同位素的通量散度、下垫面被蒸发水汽中的稳定同位素和降水中的稳定同位素等要素(Zhang et al., 2015; Yoshimura et al., 2003; 2004).与引入稳定同位素效应的GCM相比(Hoffmann et al., 1998; Xi, 2014;Jouzel et al., 1991), iAWBM简化了复杂的大气过程和水循环中水稳定同位素的分馏过程.它将单点的简单瑞利分馏模型植入到全球每个格点, 然后在每个格点及在每一时间步长利用水平衡方程分别计算水汽和水汽同位素的输送(Zhang et al., 2015; 2016).简化的模式在垂直方向上仅有一层, 大气水汽和水汽同位素成分的垂直分布被包含在垂直积分中(Zhang et al., 2015; Yoshimura et al., 2003).在简化处理下, 由对流产生的影响局地降水稳定同位素的一些因素和过程被忽略, 稳定同位素的分馏仅考虑在水平尺度下由温度所确定的凝结分馏或凝华分馏(Jouzel et al., 1987; Majoube, 1971a; 1971b).由于模式在计算大气的水平衡和水稳定同位素平衡过程中将外部气象数据作为驱动变量, 这使得iAWBM能够真实再现大气中的水循环和水稳定同位素循环(Yoshimura et al., 2003).
利用iAWBM的模拟数据, 笔者曾分析了全球降水中稳定同位素效应的空间分布特征, 并对模拟结果与全球降水同位素监测网(GNIP)的实际监测数据进行了比较(张婉君等, 2017), 结果表明, iAWBM的模拟很好地再现了全球降水中稳定同位素的纬度效应、大陆效应和高度效应;模拟的δ18O季节差的空间分布与实际分布基本对应, 在北半球低纬度地区, δ18O的季节差主要表现为负值, 而在高纬度大陆地区主要表现为正值;模拟的降水量效应主要出现在中低纬度海洋和季风区; 模拟的温度效应主要出现在中高纬度内陆地区.在一些低纬度地区, 伴随强降水量效应的出现, 温度效应也同时出现, 这与实测结果吻合(Dansgaard, 1964; Aragúas et al., 1998; Merlivat, 1979);模拟的全球大气水线的斜率和截距均与实测结果相近.
本研究在全球降水同位素空间变化的模拟和分析基础上, 利用iAWBM的模拟数据, 分析具有不同气候背景的GNIP代表站降水中δ18O的时间变化特征、降水中δ18O与温度和降水量之间的关系、区域大气水线, 并将模拟结果与实测结果进行比较, 旨在对iAWBM的模拟有效性进行评价, 改善对水循环中水稳定同位素效应的理解和认识.
2 模式设计和基本数据(Model design and basic data)稳定同位素大气水平衡模式基于大气水平衡方程、水稳定同位素平衡方程和瑞利分馏方程.由全球1.5°×1.5°的格点精度和一个平均垂直层组成(Zhang et al., 2015; 2016; Yoshimura et al., 2003).
在实施模拟之前先进行spin-up, 目的是为正式模拟提供初始值(Zhang et al., 2016).运行spin-up和正式模拟的驱动数据均取自欧洲中期数值天气预报中心ECMWF(European Centre for Medium-Range Weather Forecasts)的ERA-Interim再分析数据(降水率、蒸发率、可降水量、温度等).数据的网格水平精度为1.5°×1.5°, 时间分辨率为6 h, 时间范围从1979年1月1日0:00至2014年12月31日24:00.
模拟数据的网格精度和时间均与再分析数据相同.模拟的结果对大气降水同位素比率δp按降水量进行加权平均, 便得到各稳定同位素比率的月加权平均值.本文用于分析的模拟数据就是基于这些月平均值或月总量序列.
为了评价iAWBM模拟降水中稳定同位素时间变化的效果, 本文选取具有代表性的GNIP站点进行个案分析.代表性站点选取的依据是:①在1979—2014年期间具有相对较长的连续监测数据;②分布在不同的地区、不同的纬度、不同的海拔高度;③具有不同的气候特点;④具有不同的同位素效应, 如温度效应、降水量效应等.经过筛选, 最终选定香港、维也纳、雅库茨克、渥太华、波哥大、曼谷、昆明、哈拉雷、拉罗汤加岛等9个具有代表性的GNIP站点(图 1和表 1).
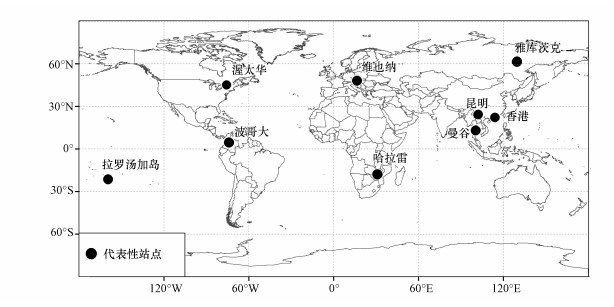 |
| 图 1 代表性站点的地理位置 Fig. 1 The map showing the locations of representative GNIP stations |
| 表 1 选择的GNIP代表性站点的基本情况 Table 1 The basic conditions of the selected representative GNIP stations |
为了定量评估模式模拟降水稳定同位素时间变化的适用性, 本文计算了模拟值与实测值之间的平均偏差(δDev), 计算公式为:
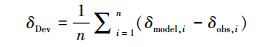
|
(1) |
式中, δmodel, i表示模式模拟的同位素比率, δobs, i表示GNIP实测的同位素比率, δDev表示模拟值与实测值的平均偏差, n为序列样本数.当δDev > 0时, 模式的模拟存在系统性高估, 反之则存在系统性低估;δDev越接近0, 系统偏差越小.
3 结果与分析(Results and analysis) 3.1 GNIP站点模拟水平的空间分布根据统计学原理, 模拟的时间序列y与实测的时间序列x之间的回归方程(y=ax+b)反映两序列之间的统计函数关系;相关系数反映两序列之间关系的密切程度;均方根误差反映模拟值对于实测值的拟合水平;平均偏差反映模拟值对于实测值的偏离情况.回归系数越接近1.0、相关系数越大、均方根误差越小、平均偏差越接近0, 则模拟值越接近实测值.以下的分析主要基于iAWBM模拟序列和GNIP实测序列之间相关关系、均方根误差、平均偏差等的统计数据.
在GNIP的数据库中, 具有连续1年及以上降水中δ18O监测数据的站点共有352个.通过计算各GNIP站点实测的逐月δ18O与在对应网格点由iAWBM模拟的逐月δ18O之间的相关系数、二者之间的均方根误差和平均偏差, 得到3个指标的全球空间分布(图 2)及相关系数和均方根误差两个指标的站点数统计分布(表 2).
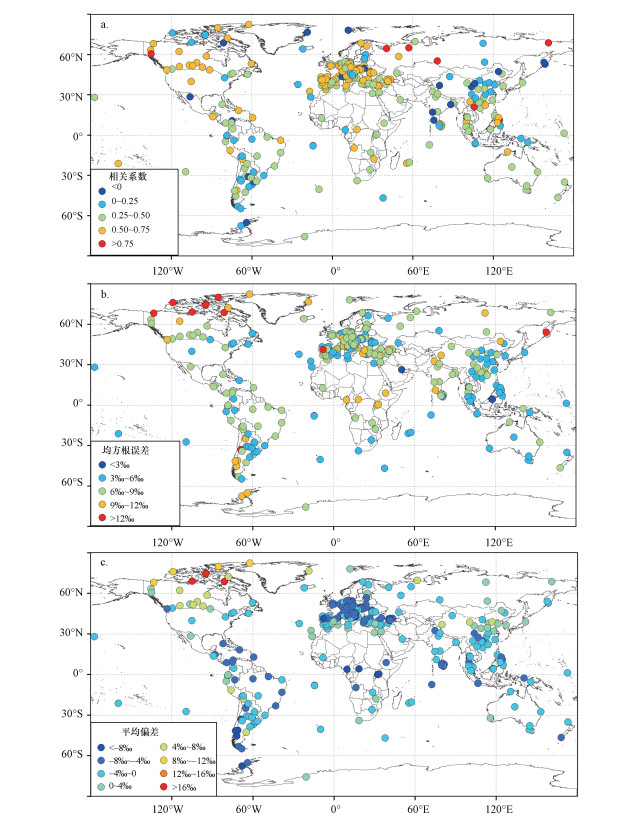 |
| 图 2 模拟的和实测的降水中δ18O之间相关系数(a)、均方根误差(b)及平均偏差(c)的空间分布 Fig. 2 The spatial distributions of correlation coefficients(a), root mean square errors(b), and mean deviation(c) between the simulated and observed δ18O time series in precipitation |
| 表 2 实测的与模拟的δ18O之间的相关系数r和均方根误差RMSE的站点数统计 Table 2 Statistics of station numbers on correlation coefficients (r) and root mean square errors (RMSE) between the observed and simulated δ18O in precipitation |
根据图 2a和表 2, iAWBM很好地模拟了全球降水中δ18O的时间变化, 全球绝大部分GNIP站模拟的与实测的月δ18O之间表现为正相关关系.在欧洲和北美地区, 实测的与模拟的δ18O之间的相关系数主要在0.25~0.75;在南美、东亚及西南太平洋地区, 相关系数在0~0.5;非洲地区的站点虽然不多, 但相关系数均大于0.最大的相关系数0.89出现在雅库茨克站(62.08°N、129.75°E, 107 m a.s.l.).在统计的352个站点中, 275个站点的相关系数在0.25以上(超过了0.05的信度检验), 占总站数的78.13%, 说明大多数站点δ18O的模拟值与实测值有一定的相关性和一致性.但另有18个站点的相关系数为负值, 主要出现在高纬度地区和中低纬度的季风活动区.
根据图 2b和表 2, 在欧洲、东亚和南美地区, 实测的与模拟的δ18O之间的均方根误差范围主要在3‰~9‰;在大洋上的一些零星站点, 均方根误差大都在6‰以下;在南极仅有的两个站点, 均方根误差在9‰~12‰.最小的均方根误差为1.45‰, 出现在阿森松岛站(7.92°S、14.42°W, 15 m a.s.l.).在所统计的站点中, 299个站点的均方根误差小于9‰, 其中13个站点的均方根误差小于3‰, 共计占总站点数的84.94%.说明大多数站点的δ18O模拟值与实测值之间的偏差是在一个合理的范围内.然而, 在加拿大北部地区, 均方根误差存在系统性的偏高, 例如, 加拿大北极区的坚决湾站(74.72°N、94.98°W, 67 m a.s.l.)的均方根误差高达21.2‰.
根据图 2c, 全球站点模拟值与实测值的平均偏差范围在-10.81‰~19.77‰, 最大的正偏差(19.77‰)出现在坚决湾站(74.72°N、94.98°W, 67 m a.s.l.), 最小的负偏差(-10.81‰)出现在智利的蒙特港站(41.47°S、72.93°W, 13 m a.s.l.).在北美洲和亚欧大陆的中高纬地区, 平均偏差为正值, 说明模式对这些区域降水稳定同位素的模拟存在系统性高估.全球81.53%的站点平均偏差为负值, 说明大多数地区的降水稳定同位素被低估.高纬度地区相关系数偏小、均方根误差和平均偏差较大的原因与iAWBM的设计有关.在iAWBM的模拟方案中, 为了满足差分格式收敛的必要条件, 人为地规定高纬度地区的水汽同位素为一常数值(Zhang et al., 2015; 2016).这种简化可能导致了在高纬度地区模拟结果的不确定性.
3.2 模拟的与实测的降水中δ18O的平均季节变化的比较水稳定同位素的季节变化与自然环境要素的季节变化密切相关, 是各类水同位素动力模式着力捕捉的最基本的自然周期(Xi, 2014).图 3分别给出了9个GNIP代表站实测的及在对应网格点由iAWBM模拟的月平均δ18O和相关气象要素的季节变化.9个站点实测的和模拟的δ18O标准差及它们之间的均方根误差、平均偏差列于表 3.
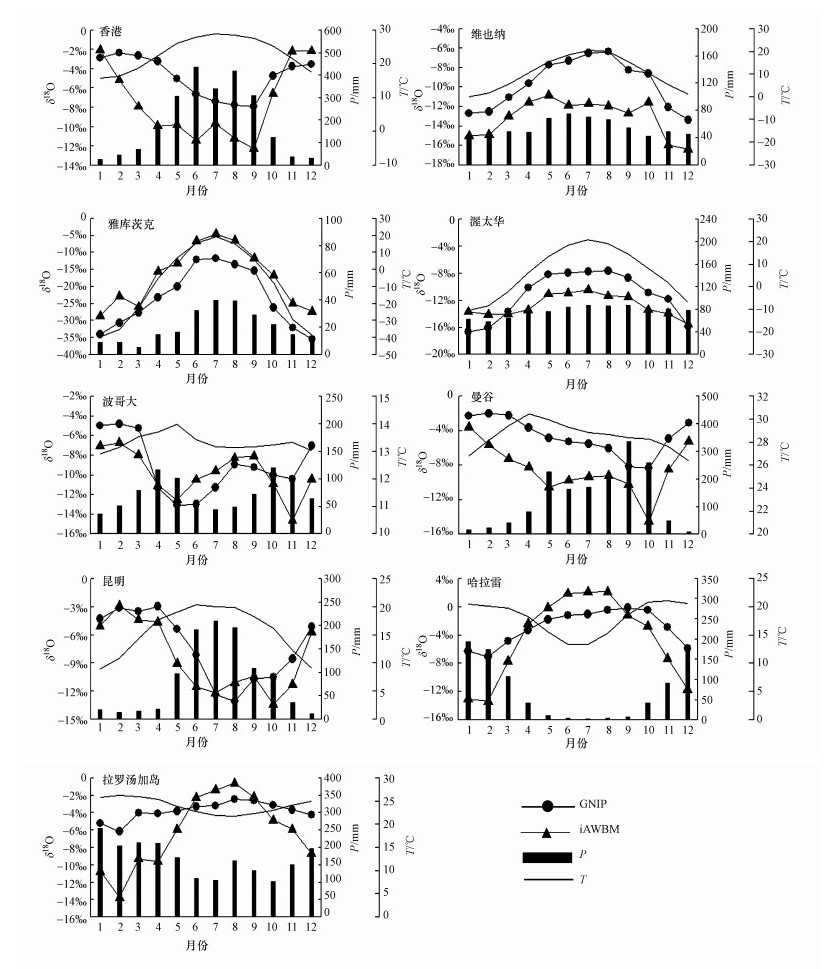 |
| 图 3 选择的9个代表站实测的与模拟的降水中δ18O的平均季节变化 Fig. 3 Observed and simulated seasonality of δ18O in precipitation at 9 representative GNIP stations |
| 表 3 代表站实测的与模拟的降水中平均δ18O的统计数据 Table 3 Statistics of observed and simulated δ18O in precipitation at 9 representative GNIP stations |
位于东亚季风区的香港站实测的温度(T)和降水量(P)具有明显的季节变化, 雨热同期, 降水中的δ18O呈现夏季低、冬季高的特点.其中, 实测的δ18O最大值(-2.35‰)出现在2月, 实测的δ18O最小值(-7.93‰)出现在9月.模拟结果很好地再现了δ18O的季节变化特点, 降水同位素夏季被贫化冬季被富集的特点被模拟出.其中, 模拟的δ18O最大值(-2.07‰)出现在1月, 与实际出现时间仅差1个月;模拟的δ18O最小值(-12.29‰)出现在9月, 与实际出现时间相同.比较而言, 模拟值的标准差大于实测值的标准差.由于大部分月份模拟值低于实测值, 二者的平均偏差为-2.71‰, 均方根误差达到3.77‰.
维也纳站具有全球最长的降水同位素记录,该站降水中稳定同位素与温度的季节变化同步, 表现为暖季被富集冷季被贫化的基本特点.其中, 实测的最大δ18O(-6.36‰)出现在8月, 实测的最小δ18O(-13.40‰)出现在12月.尽管模拟结果很好地再现了δ18O的季节变化, 且最小δ18O(-16.40‰)的出现时间与实际出现时间相同, 但最大δ18O(-10.87‰)出现的时间提前到5月.相对于实测值, 全年各月的模拟值均偏低, 且变化幅度偏小.
位于东西伯利亚的雅库茨克站具有雨热同期、四季分明的气候特点.可以看出, 无论是实测的还是模拟的降水δ18O的季节变化均与温度的季节变化一致, 三者的最高值和最低值的出现时间基本吻合.然而, 实测值与模拟值之间的均方根误差达到6.78‰, 是9个站点中最大的.该站的平均偏差达到6.48‰, 说明模式高估了降水同位素实际的变化.
渥太华站的降水同位素具有与雅库茨克站降水同位素相似的季节变化特点.由于降水量的季节变化较小, 实测的降水δ18O季节变化幅度小于雅库茨克站.尽管模式再现了渥太华站降水同位素的季节变化, 但模拟的降水同位素的季节变化幅度及累月平均值明显小于实测结果.
位于苏马帕斯高原谷地的波哥大站具有赤道地区特有的气候特点, 平均温度、平均降水量及平均降水同位素均表现出明显的双峰型.模拟的降水同位素很好地再现了双峰型的季节变化特点.其中, 模拟的两个δ18O极大值分别出现在2月和8月, 两个δ18O极小值分别出现在5月和11月, 与实测的出现时间大致相当.波哥大站模拟值的标准差与实测值的标准差大致相当, 均方根误差(2.18‰)较小, 平均偏差仅为-0.71‰.
曼谷站的平均温度和平均降水量的季节变化与波哥大非常相似, 呈现明显的双峰型.由于海拔高度较低, 各月平均温度和平均降水量均偏大.然而, 实测的降水同位素并未完全响应双峰型的季节变化特点, 而是显示单峰型.其中, 实测的最大δ18O(-2.04‰)出现在2月, 实测的最小δ18O(-8.35‰)出现在10月.模拟的降水同位素同样显示了单峰型的季节变化, 其中, 模拟的最大δ18O(-3.6‰)出现在1月, 模拟的最小δ18O(-14.55‰)出现在10月.
位于云贵高原的昆明站受高原季风的影响, 干湿季分明.实测的δ18O季节变化显示:伴随暖半年(5—10月)明显偏多的降水, 降水同位素明显被贫化, 伴随冷半年(11—4月)明显偏少的降水, 降水同位素明显被富集.其中, 实测的最大δ18O(-3.00‰)出现在2月, 实测的最小δ18O(-13.10‰)出现在10月.模拟结果很好地再现了实测的δ18O季节变化.其中, 模拟的最大值(-2.90‰)和最小值(-13.42‰)的出现时间均与实际出现时间相同.比较显示, 实测的与模拟的δ18O标准差较接近, 2.04‰的均方根误差和-1.16‰的平均偏差相对较小.
位于津巴布韦北部的哈拉雷站属热带草原气候, 夏季温暖湿润, 冬季凉爽干燥.实测的降水同位素的季节变化正好与温度和降水量的季节变化相反, 暖半年明显被贫化, 冷半年明显被富集.其中, 实测的最大δ18O(-0.17‰)出现在9月, 实测的最小δ18O(-7.09‰)出现在2月.模拟的降水同位素的季节变化与实测结果基本一致, 但变化幅度略大, 累月平均值略小.模拟的最大δ18O(2.09‰)出现在8月, 比实际出现时间提前1个月, 模拟的最小δ18O(-13.40‰)出现在2月, 与实际出现时间相同.
位于南太平洋的拉罗汤加岛站全年温度较高, 降水量较大, 但它们的季节差异都较小.与温度、降水量的季节变化相适应, 实测的降水同位素的季节变化也较小.其中, 实测的最大δ18O(-2.47‰)出现在8月, 实测的最小δ18O(-6.18‰)出现在2月.尽管模拟结果放大了降水同位素的季节变化, 但模拟的最大δ18O(-0.63‰)和最小δ18O(-13.77‰)的出现时间均与实际出现时间相同.
根据对9个代表站的分析可以看出, iAWBM的模拟较好地再现了降水稳定同位素的季节变化;除了哈拉雷和拉罗汤加岛站外, 其它各站实测值的标准差和模拟值的标准差大致相当, 且模拟值与实测值之间的均方根误差均在一个合理的范围.除雅库茨克站降水稳定同位素的季节变化被高估外, 其余站点均被低估.
3.3 模拟的与实测的降水中δ18O的逐月变化比较将9个GNIP代表站实测的和由iAWBM在对应网格点模拟的逐月δ18O点绘于图 4, 并计算了二者的一元线性回归方程、相关系数r、均方根误差RMSE及平均偏差δDev.
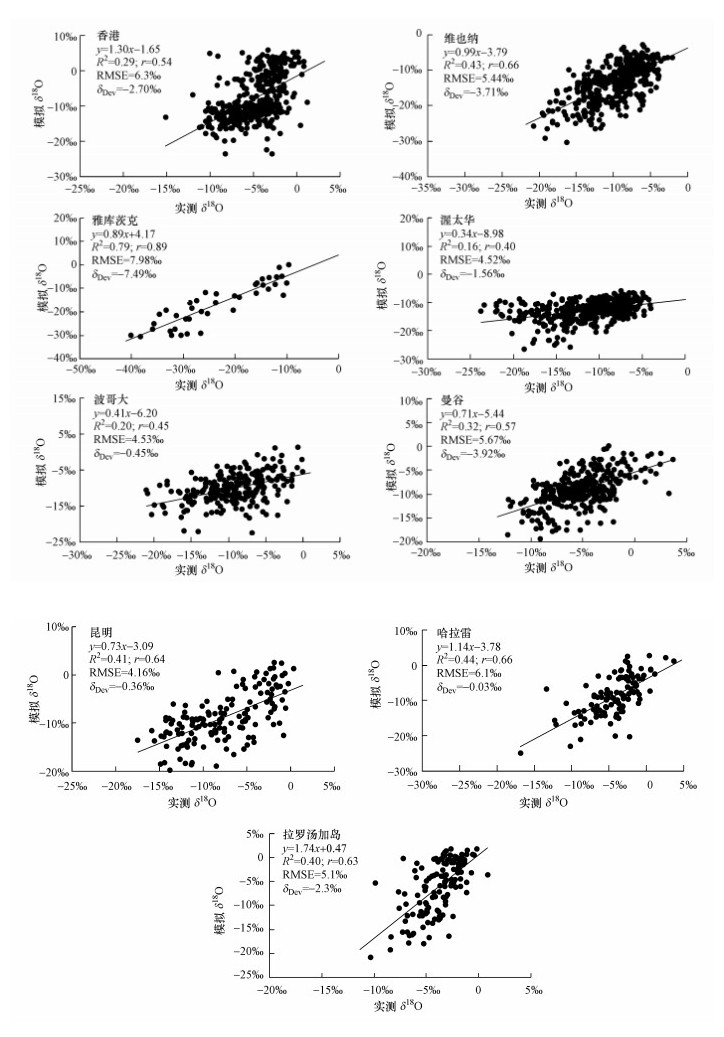 |
| 图 4 选择的9个代表站模拟的与实测的降水中δ18O的相关散布 Fig. 4 Correlated scatters of the simulated versus the observed δ18O in precipitation at 9 representative GNIP stations |
从模拟的依实测的δ18O的回归方程来看, 维也纳、雅库茨克、哈雷拉3个代表站的模拟效果相对最好, 它们的回归方程斜率最接近对角线;香港、曼谷、昆明3个代表站的模拟效果次之;渥太华、波哥大、拉罗汤加岛等3个代表站的模拟效果稍差, 它们的回归方程斜率较大地偏离了对角线.
从相关程度来看, 雅库茨克站模拟的与实测的δ18O序列之间的正相关系数最大, 达到0.89, 远超过0.001的信度, 但样本数只有40个;其它8个代表站的样本数均在100以上, 且相关系数也都超过了0.001的信度.比较而言, 香港、维也纳、曼谷、昆明、哈拉雷、拉罗汤加岛6个站的相关系数更大一些, 信度也更高一些.
从模式的拟合水平来看, 渥太华、波哥大、昆明3个站的RMSE最小, 均不到5.0‰;香港、维也纳、曼谷、哈拉雷、拉罗汤加岛5个站的RMSE在5.0‰~7.0‰之间;雅库茨克站的RMSE在9个代表站中是最大的, 达到了7.98‰.
从平均偏差来看, 仅雅库茨克站的平均偏差为正值且较大, 说明模式高估了该站点降水稳定同位素的平均组成;其余站点的平均偏差均为负值, 说明这些站点的值被低估;模式模拟的系统偏差较小的站点是波哥大、昆明和哈拉雷站, 它们的平均偏差非常接近0.
对照GNIP实测序列, 且利用泰勒图(略)进行综合比较.在9个代表站逐月δ18O长序列的模拟中, 除拉罗汤加岛外, 其它8个站的模拟效果并无显著差异, 说明iAWBM模拟降水中稳定同位素的时间变化是可信的.
3.4 模拟的与实测的温度效应的比较降水中的稳定同位素比率与近地面气温之间显著的正相关关系被定义为温度效应.温度效应主要出现在中高纬度的内陆(Dansgaard, 1964).9个被选择的代表站中具有温度效应的站点是维也纳、雅库茨克、渥太华和曼谷站.分别将4个代表站实测的和模拟的δ18O与温度T的月数据点绘于图 5, 并计算了二者的一元线性回归方程和相关系数(表 4).
 |
| 图 5 具有温度效应的4个GNIP代表站模拟的与实测的降水中δ18O依温度T的相关散布 Fig. 5 Correlated scatters of the simulated and observed δ18O in precipitation versus temperature at 4 representative GNIP stations with temperature effect |
| 表 4 具有温度效应的4个GNIP代表站实测的与模拟的降水中δ18O-T相关关系的比较 Table 4 Comparisons between the observed and simulated δ18O-T correlations at 4 representative GNIP stations with temperature effect |
在维也纳站, 根据模拟值计算的δ18O-T回归方程与根据实测值计算的δ18O-T回归方程具有较好的一致性, 且都显示明显的温度效应.然而, 模拟的斜率小于实测的斜率, 并且模拟的截距大于实测的截距.尽管由模拟值和由实测值计算的δ18O-T之间的相关系数均达到0.001的信度, 但前者只有后者的1/2, 说明iAWBM在维也纳站的δ18O模拟相较于实测序列具有较大的离散性.
在雅库茨克站, 模拟的δ18O-T回归方程非常好地再现了实际的温度效应, 且0.93的相关系数与实测的相关系数量级相当, 均超过0.001的信度.
尽管渥太华站显著的温度效应被模拟出, 但模拟的回归系数斜率仅是实际斜率的约1/2, 且由模拟序列计算的δ18O-T之间的相关系数也只有实测值的1/2.
与位于中高纬度内陆的前3个站相比, 位于热带地区的曼谷站具有一定程度的温度效应.该地温度效应的产生与赤道辐合带季节性位移产生的干湿季有关(Zhang et al., 2016), 即使是这种不显著的温度效应也被iAWBM捕捉到.模拟的相关系数的量级与实测的相关系数相当, 但模拟的回归系数略小于实测值.
3.5 模拟的与实测的降水量效应的比较降水中稳定同位素比率与降水量之间显著的负相关关系被定义为降水量效应.降水量效应主要出现在中低纬度海洋、海岛和季风区(Dansgaard, 1964).9个代表站中具有降水量效应的站点分别是香港、波哥大、曼谷、昆明、哈拉雷和拉罗汤加岛站.分别将这6个代表站实测的和模拟δ18O与降水量P的月数据点绘于图 6, 并计算了二者的一元线性回归方程和相关系数(表 5).
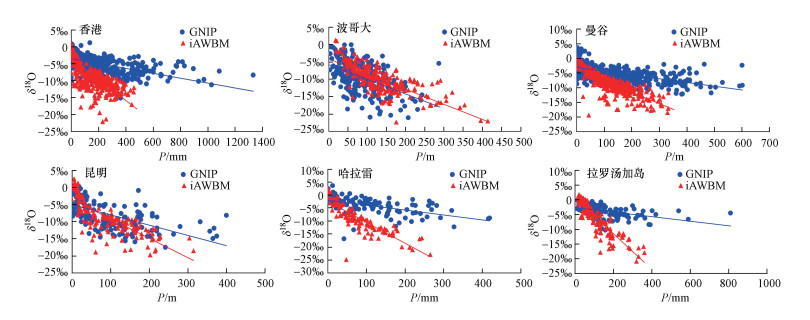 |
| 图 6 具有降水量效应的6个GNIP代表站模拟的与实测的降水中δ18O依降水量P的相关散布 Fig. 6 Correlated scatters of the simulated and observed δ18O in precipitation versus precipitation at 6 representative GNIP stations with amount effect |
| 表 5 具有降水量效应的6个GNIP代表站实测的与模拟的降水中δ18O-P相关关系的比较 Table 5 Comparisons between the observed and simulated δ18O-P correlations at 6 representative GNIP stations with amount effect |
6个GNIP站实测的降水同位素均具有显著的降水量效应, 各站的负相关系数也均超过0.01的信度.对应的6个站模拟的降水同位素都很好地再现了实际存在的降水量效应.然而, 除了波哥大站模拟的δ18O-P回归系数与实测的回归系数一致以外, 其它5个站模拟的回归系数均比实测的回归系数大1~5倍, 尤其是拉罗汤加岛站.说明模拟的降水同位素对降水量具有更强的依赖性,这种强依赖性也同时表现在各站模拟的降水量效应具有更大的δ18O-P相关系数.
尽管模式的模拟大多高估了降水量对降水同位素的贫化作用, 但考虑到水循环中水稳定同位素分馏过程及影响因子的复杂性, iAWBM在模拟站点的降水量效应方面的能力还是很强大的.
3.6 模拟的与实测的大气水线MWL的比较分别将9个代表站实测的和模拟的δ18O与δ2H的月数据点绘于图 7, 并将计算的各站δ18O与δ2H之间的一元线性回归方程和相关系数列于表 6.
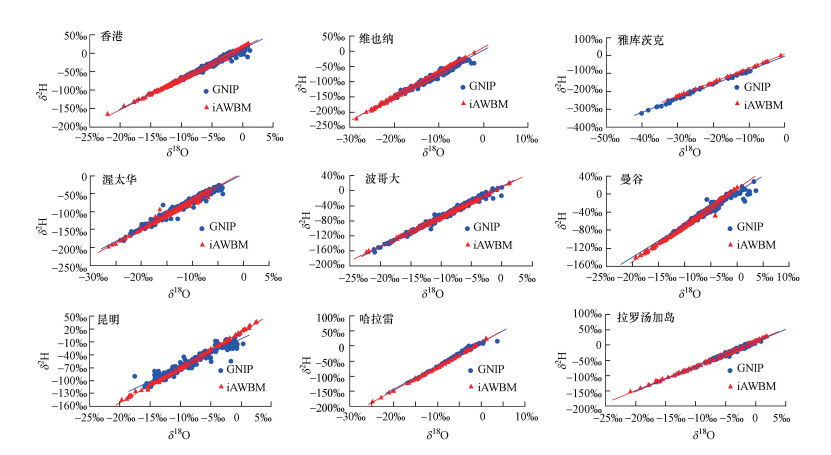 |
| 图 7 GNIP代表站模拟的与实测的降水中δ2H-δ18O的相关散布 Fig. 7 Correlated scatters of the simulated and observed δ2H in precipitation versus δ18O at 9 representative GNIP stations |
| 表 6 GNIP代表站实测的与模拟的降水中δ2H-δ18O相关关系的比较 Table 6 Comparisons between the observed and simulated δ2H-δ18O correlations at 9 representative GNIP stations |
降水中δ2H与δ18O之间存在非常好的线性关系, 这种关系被定义为大气水线(MWL) (Dansgaard, 1964).MWL的斜率反映稳定同位素2H与18O之间分馏效应的对比关系.由Craig(1961)根据在全球取得的400多个水样计算的全球MWL为δ2H=8.0δ18O+10.0‰.这个结果被认为是水循环中水稳定同位素平衡分馏的结果(Craig, 1961; Merlivat et al., 1979).
理论的分析发现, 来自海洋暖湿水汽影响的大气具有不稳定能量高、对流性强、空气湿度大的特点, 因此, MWL的斜率较高(Zhang et al., 2003).例如, 在香港、曼谷、昆明和拉罗汤加岛站模拟的大气水线斜率均明显超过8.0;来自大陆蒸散发水汽影响的大气具有平流性强、空气湿度小、云下蒸发强的特点, 因此, MWL的斜率较低(Zhang et al., 2003).例如, 在雅库茨克、渥太华和波哥大站模拟的大气水线斜率均明显低于8.0;在海洋水汽和大陆水汽均有明显影响的站点, 如维也纳和哈拉雷站, 模拟的MWL的斜率接近8.0.
然而, 除了受大尺度下垫面类型、大气环流的影响之外, MWL还受局地气象条件的制约.根据表 6, 在明显受海洋性水汽影响的香港和拉罗汤加岛站, 模拟的与实测的MWL具有非常好的一致性, 模拟的和实测的MWL斜率均大于8.0, 但曼谷和昆明站的MWL斜率被高估;在大陆性气团控制下的雅库茨克站和渥太华站, 模拟的与实测的MWL具有较好的一致性, 模拟的和实测的MWL斜率均小于8.0, 但波哥大站的MWL斜率被低估;在海洋、陆地水汽均有明显影响的维也纳和哈拉雷站, 模拟的MWL斜率均接近8.0, 但实测的MWL斜率均低于8.0.
4 讨论(Discussion)利用稳定同位素水平衡模式的模拟数据, 分析了GNIP代表站降水中δ18O的时间变化特征、降水中δ18O与温度和降水量之间的关系及区域大气水线, 模拟结果与实测结果进行了比较, 旨在对iAWBM的模拟有效性进行评价, 改善对水循环中水稳定同位素效应的理解和认识.
尽管iAWBM可以再现水循环中降水同位素的时间变化特征, 揭示不同气候条件下的稳定同位素效应.但可以看到, iAWBM的模拟结果与实际结果还是存在着一些差异.产生差异的原因与模式的结构、稳定同位素模拟方案、模式的精度等有关.
首先, iAWBM的物理过程是建立在水平衡和水稳定同位素平衡的基础上.这种处理一方面简化了复杂的大气过程和水稳定同位素分馏过程;但另一方面, 由于忽略了一些影响要素, 也使得iAWBM的模拟值与实测值的偏差增大.
第二, 一些模拟结果与实测结果不一致的原因很大程度上可能是由于模拟空间和实际空间尺度下水汽过程的细节和模式的精度方面存在差别.由于iAWBM是格点模式, 模拟的结果代表网格区的平均状况, 因此, 很难逼近在空间点的观测值.
第三, 大气中的水汽及水汽同位素主要源于下垫面的蒸发.在iAWBM的模拟中, 从下垫面蒸发的水汽同位素的时间变化被假设与大气水汽同位素的时间变化同步, 下垫面被蒸发水汽中的稳定同位素丰度仅与下垫面性质有关.这种计算方案与实际情况肯定存在差异, 不可避免地影响降水同位素模拟的准确性.
第四, iAWBM未考虑云下雨滴因蒸发而产生的稳定同位素富集效应, 这也直接导致在iAWBM的模拟中, 降水同位素明显被低估、降水量效应的贫化程度明显被高估.
第五, iAWBM假设云中的动力分馏是在冰面过饱和条件下发生, 并且用冰面过饱和比Si=1.0-0.003T)来度量动力分馏的强弱.由于降水同位素的模拟对冰面过饱和比具有敏感性, 因此, 简单、一致化的处理必然会导致模拟的稳定同位素效应与实际情况存在差异.
5 结论(Conclusions)1) 研究结果表明, iAWBM较好地再现了全球降水中δ18O的时间变化.在具有长期监测序列的352个GNIP站点中, 275个站点模拟的与实测的δ18O之间的相关系数在0.25以上(超过0.05的信度), 占总数的78.13%;模拟的与实测的δ18O之间均方根误差小于9‰的站点数达299个, 占总站点数的84.94%.说明大多数站点δ18O的模拟值与实测值具有一定的相关性和一致性.全球81.53%的站点平均偏差为负值, 说明模式对全球大部分地区降水同位素的模拟存在系统性低估.
2) 对于选择的具有不同气候特点、不同地理位置、不同降水同位素效应的9个GNIP代表站, 降水同位素暖季被富集冷季被贫化的季节变化特点(如维也纳、雅库茨克和渥太华站)、降水同位素暖季被贫化冷季被富集的季节变化特点(如香港、曼谷和拉罗汤加岛站)、降水同位素湿季被贫化干季被富集的季节变化特点(如昆明和哈拉雷站)及降水同位素双峰型的季节变化特点(如波哥大站)均被模拟出.除哈拉雷和拉罗汤加岛站外, 其它各站实测值的标准差和模拟值的标准差大致相当, 且模拟值与实测值之间的均方根误差均在一个合理的范围.除雅库茨克站降水稳定同位素的季节变化被高估外, 其余站点均被低估.
3) 在降水同位素长期变化的模拟中, 所有9个代表站模拟的与实测的降水同位素序列之间的相关系数均超过0.001的信度, 均方根误差小于8.0‰.说明iAWBM具有模拟不同气候区降水中稳定同位素时间变化的能力.
4) iAWBM很好地再现了出现在维也纳、雅库茨克和渥太华站的显著温度效应, 出现在香港、波哥大、昆明、哈拉雷和拉罗汤加岛站的降水量效应, 以及出现在曼谷站的温度效应和降水量效应共存的特点.与站点的实际情况相比, 模式模拟的温度效应减弱, 模拟的降水量效应增强.
5) iAWBM的模拟表明, 海洋暖湿水汽影响下的MWL斜率较高, 通常大于8.0, 如香港和拉罗汤加岛站;大陆蒸散发水汽影响下的MWL斜率较低, 通常小于8.0, 如雅库茨克和渥太华站;平衡条件下产生的MWL斜率接近8.0.这些模拟结果均被代表站的实际MWL所证实.维也纳、曼谷、昆明和哈拉雷4个站的MWL斜率被高估, 波哥大站的MWL斜率被低估.
Aragúas L, Froehlich K, Rozanski K. 1998. Stable isotope composition of precipitation over southeast Asia[J]. Journal of Geophysical Research, 103: 28721–28742.
DOI:10.1029/98JD02582
|
Craig H. 1961. Isotopic variations in meteoric water[J]. Science, 133: 1702–1703.
DOI:10.1126/science.133.3465.1702
|
Dansgaard W. 1964. Stable isotopes in precipitation[J]. Tellus, 16(4): 436–468.
DOI:10.3402/tellusa.v16i4.8993
|
Hoffmann G, Werner M, Heimann M. 1998. Water isotope module of the ECHAM atmospheric general circulation model:a study on timescales from days to several years[J]. Journal of Geophysical Research, 103: 16871–16896.
DOI:10.1029/98JD00423
|
Jouzel J, Koster R D, Suozzo R J, et al. 1991. Simulations of the HDO and H218O atmospheric cycles using the NASA GISS GCM:sensitivity experiments for present-day conditions[J]. Journal of Geophysical Research, 94: 7495–7507.
|
Jouzel J, Merlivat L. 1984. Deuterium and oxygen-18 in precipitation:modeling of the isotopic effects at snow formation[J]. Journal of Geophysical Research, 80: 5015–5030.
|
Jouzel J, Russell G L, Suozzo R J. 1987. Simulations of the HDO and H218O atmospheric cycles using the NASA-GISS general circulation model-the seasonal cycle for present day conditions[J]. Journal of Geophysical Research, 92: 14739–14760.
DOI:10.1029/JD092iD12p14739
|
Majoube M. 1971a. Fractionnement en oxygene 18 et en deuterium entre l'eau et savapeur[J]. The Journal of Chemical Physics, 10: 1423–1436.
|
Majoube M. 1971b. Fractionnement en oxygene 18 entre la glace et la vapeur d'eau[J]. The Journal of Chemical Physics, 68: 625–636.
|
Merlivat L, Jouzel J. 1979. Global climatic interpretation of the deuterium-oxygen 18 relationship for precipitation[J]. Journal of Geophysical Research, 84: 5029–5033.
DOI:10.1029/JC084iC08p05029
|
Xi X. 2014. A review of water isotopes in atmospheric general circulation models:recent advances and future prospects[J]. International Journal of Atmospheric Sciences, 3(3): 1–16.
|
Yoshimura K, Oki T, Ohte N, et al. 2003. A quantitative analysis of short-term 18O variability with a Rayleigh-type isotope circulation model[J]. Journal of Geophysical Research: 108.
DOI:10.1029/2003JD003477
|
Yoshimura K, Oki T, Ichiyanagi K. 2004. Evaluation of two-dimensional atmospheric water circulation fields in reanalyses by using precipitation isotopes databases[J]. Journal of Geophysical Research: 109.
DOI:10.1029/2004JD004764
|
Zhang X P, Yao T D, Liu J M, et al. 2003. Simulations of stable isotopic fractionation in mixed cloud in middle latitudes-taking the precipitation at Urumqi as an example[J]. Advances in Atmospheric Sciences, 20(2): 261–268.
DOI:10.1007/s00376-003-0012-9
|
Zhang X P, Guan H D, Zhang X Z, et al. 2015. Simulation of stable water isotopic composition in the atmosphere using an Isotopic Atmospheric Water Balance Model[J]. International Journal of Climatology, 35(6): 846–859.
DOI:10.1002/joc.2015.35.issue-6
|
Zhang X P, Guan H D, Zhang X Z, et al. 2016. Numerical experiments on the impacts of surface evaporation and fractionation factors on stable isotopes in precipitation[J]. Asia-Pacific Journal of Atmospheric Sciences, 52(3): 327–339.
DOI:10.1007/s13143-016-0008-x
|
张婉君, 章新平, 姚天次, 等. 2017. 降水稳定同位素的iAWBM模拟及其与GNIP实测值的比较[J]. 环境科学学报, 2017, 37(2): 538–544.
|
周淑贞. 1997. 气象学与气候学(第三版)[M]. 北京: 高等教育出版社: 200–225.
|
 2018, Vol. 38
2018, Vol. 38


