2. 水利部国际经济技术合作交流中心, 北京 100053;
3. 云南省环境监测中心站, 昆明 650000
2. International Economic & Technical Cooperation and Exchange Center, Ministry of Water Resources, Beijing 100053;
3. Yunnan Environmental Monitoring Center Station, Kunming 650000
营养盐基准是指使水体满足指定功能时营养盐浓度的最大值(US EPA, 1998),是进行水质目标管理和保障生态健康的基础(Heiskary and Bouchard, 2015; Huo et al., 2017).营养盐基准由2个基本要素构成:空间尺度和浓度限值(Evans-White et al., 2013; Rohm et al., 2002).其中,空间尺度规定了营养盐基准适用的空间范围,合理的空间尺度是保证浓度限值有效性的基础.全国性营养盐基准由于忽视了气候、植被覆盖等因子的空间异质性,而逐渐被以生态分区为空间尺度的区域性营养盐基准替代(Rohm et al., 2002; Stoddard, 2004).但生态分区内存在局部驱动因子的空间异质性(Hamil et al., 2016).局部驱动因子是指在水体个体尺度上存在差异的因子(Fergus et al., 2011; Olson and Hawkins, 2013),如水深、水面面积、流域面积等;局部驱动因子的空间异质性可能会影响营养盐与管理终点的响应关系或营养盐浓度的波动.Wagner等(2011)对芬兰35个生态分区湖泊的叶绿素a(Chla)与总磷(TP)之间的对数线性关系进行了研究,发现截距与局部驱动因子有关;Read等(2015)对2007年美国湖泊评价数据的分析结果表明,局部驱动因子对总氮(TN)和TP波动性的解释率分别高达60%和56%.这些研究虽然强调了局部驱动因子的重要性,却未评估区域性营养盐基准的适用性.一些研究者建立了针对单个水体的专一性营养盐基准(Xu et al., 2015),相对于区域性营养盐基准而言具有更高的准确性(Mclaughlin, 2014).然而这些研究未与区域性营养盐基准进行比较,并不能确认区域性营养盐基准的适用性.尽管区域性营养盐基准受到了来自局部驱动因子空间异质性的挑战,然而对其在个体尺度上的适用性进行评估的研究尚不多见.
探究区域性营养盐基准的适用性对于我国水污染防治具有重要意义(Han et al., 2016).一方面,部分流域的水质监测数据稀缺,难以满足水质目标管理的需求(Chen et al., 2017);如果区域性营养盐基准可适用于生态分区内特定水体类型的全部水体,对于数据稀缺的水体则可直接采用该基准,从而节约水质数据采集的时间和资金.但另一方面,如果区域性营养盐基准不具有适用性而仍采用之,则可能会误导污染防治决策.考虑到我国湖泊富营养化的严峻形势及达到营养盐浓度背景值的艰巨性(Le et al., 2010),参照(Huo et al., 2013; Zhang et al., 2014)的研究,本文选择压力响应模型法作为浓度限值的推导方法,以Chla为管理终点;由于TN和TP是导致湖泊富营养化的主要因子和湖泊浮游藻类生长的主要限制性因子(Conley et al, 2009),因而本文选择TN和TP为营养盐指标.压力响应模型将营养盐与管理终点的响应关系定量化(McLaughlin and Reckhow, 2017).生态分区内不同湖泊响应关系的差异可能源于:①随机因素(例如样品测试时的随机误差)导致的差异,②局部驱动因子导致的较小的差异,但不足以影响区域性营养盐基准的适用性,③局部驱动因子导致的较大的差异,且使区域性营养盐基准不再适用.在实践中难以对上述情况进行区分,因而根据湖泊响应关系的差异难以判断区域性营养盐基准的适用性,急需采用科学的方法对响应关系的差异性(或相似性)进行探究.
本研究提出一种基于响应关系的聚类方法(Relationship-based Clustering Approach, RCA),用于分析生态分区内湖泊Chla与营养盐响应关系的相似性,进而评价区域性营养盐基准的适应性.如果RCA的结果支持将全部湖泊聚为一类,说明响应关系的差异由随机因素引起,或说明局部驱动因子未影响区域性营养盐基准的适用性;否则说明局部驱动因子对营养盐基准有较大影响,以致区域性营养盐基准不再完全适用.由于该方法需要得到每个湖泊Chla与营养盐的响应关系,因而需要长时间的监测数据.基于Huo等(2014)对我国湖泊生态分区的划分和数据的可获得性,本研究选择我国云贵高原湖区和东部平原湖区作为研究对象.
2 材料和方法(Materials and methods) 2.1 研究对象本研究选择了云贵高原湖区(2006—2015年,数据来源为云南省环境监测中心站)和东部平原湖区(2010—2016年,数据来源为环境监测总站)重点湖泊的月水质数据,指标包括TN、TP和Chla.营养盐对Chla的限制性作用是建立压力响应模型的前提(Dodds and Welch, 2000),本研究采用偏相关分析法对营养盐的限制性作用进行分析(Kim, 2015),通过显著性检验(P<0.05)的湖泊方能用于建立压力响应模型.两个生态分区中筛选出的受TN和TP限制的湖泊个数均为5个(图 1).入选湖泊的水质数据缺失比例很小(总计为1.3%),可采用中位数平滑法进行缺失数据的插补(Tuckey, 1977;梁中耀等, 2014),插补后的数据用于RCA分析.
 |
| 图 1 湖泊的空间分布 Fig. 1 Locations map of lakes |
本研究提出的RCA包括层次聚类和模型选择两个过程(图 2).层次聚类的目的是根据响应关系对湖泊进行聚类,其结果展示不同类别个数对应的聚类状态;模型选择过程则根据信息准则选择最佳类别个数.
 |
| 图 2 RCA流程图 Fig. 2 Flow chart of the proposed RCA |
为满足压力响应模型的正态性和方差齐次性假设,对原数据进行以自然常数为底的对数变换(Oliver et al., 2017),并采用线性混合效应模型(LMM, Linear Mixed-effect Model)模拟类别个数大于1时的响应关系.LMM是一种包含压力变量对响应变量的固定效应和随机效应的统计学模型(Bates et al., 2015),其随机效应表示生态分区内局部驱动因子的空间异质性对响应关系的影响(Hamil et al., 2016).作为无信息先验时贝叶斯层次模型参数的粗略估计,LMM可提高参数估计的准确性(Qian et al., 2015).本研究中建立的LMM如下:

|
(1) |
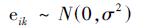
|
(2) |
式中,xik和yik分别表示对数变换后的营养盐(TN或TP)和Chla浓度,i (1 ≤ i ≤ Q)为类别标识,Q为类别个数,k为特定类别的观测数据标识;参数α0和β0分别表示截距和斜率的固定效应,αi和βi表示类别i的随机效应;eik表示残差.类别i的响应关系的截距和斜率分别为α0 + αi和β0 + βi.
聚类开始前(循环次数I为0),每个湖泊被视为一个类别,此时类别个数(Q)等于湖泊个数(P).本研究采用生态分区内湖泊的平均绝对百分误差(MAPE, Mean Absolute Percentage Error)作为聚类依据(Bennett et al., 2013; Liu et al., 2017):对于每次循环,具有最小MAPE的2个类别聚为新类.一次循环对应一次聚类,聚类过程共需P-1次聚类(图 2a).
假设在新的一次聚类开始前,湖泊的聚类状态为LQin={(l1, …, lP)},则每次尝试形成的新聚类状态可表示为LQ(u, v) ={ …, (lu, lv), …},其中lu和lv表示被聚为新类的2个类别.通过建立和求解压力响应模型,可得在聚类状态为LQ(u, v) 时第p个湖泊的MAPE:

|
(3) |
式中,Np表示第p个湖泊的样本容量,b表示观测数据标识,ypb和

|
(4) |
每次聚类需建立CQ2个新聚类状态,聚为新类的两个类别U和V满足:
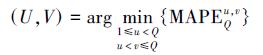
|
(5) |
对应的聚类状态可表示为LQbest={ …, (lU, lV), … }.当Q > 1时,LQ-1in=LQbest,并进入下一次聚类.聚类过程结束后,全部湖泊聚为一类,即L2best= {(l1, …, lP)};此时,LMM变为线性回归模型:

|
(6) |
此即为区域响应关系模型.
与传统的聚类方法,如层次聚类法(Altman and Krzywinski, 2017)、k均值聚类(Barrero et al., 2015)、基于模型的聚类方法(Ingrassia et al., 2015)等相比,RCA的层次聚类过程具有如下3个方面的特征:①聚类的依据为对响应变量观测数据的拟合效果,而非观测数据;②聚类状态确定后,需建立新的压力响应模型进行下一次聚类,而非确定新的数据中心点;③聚类结果为对响应关系的聚类,而非对状态变量的聚类.显然,当不考虑任何压力变量时,层次聚类过程即成为以均值为中心的层次聚类法(Murtagh and Contreras, 2017),因而可视其为层次聚类法的扩展.此外,本研究提出的RCA需构建压力响应模型,因而亦属基于模型的聚类方法的范畴(Ingrassia et al., 2015),此亦为RCA模型选择过程的必要条件.
2.2.2 模型选择过程在层次聚类过程中,随着类别个数的减少,模型参数个数减少,拟合效果变差,因而仅仅根据衡量模型拟合效果的统计量(如MAPE)无法筛选出最佳模型;此时,模型选择过程应兼顾模型的复杂度和拟合效果(Piou et al., 2009).赤池信息准则(AIC, Akaike Information Criterion)能兼顾模型的复杂度和拟合效果,已被广泛应用于LMM的优选中;AIC值越小,对应模型被选择的优先级越高(Hofmeister et al., 2015; Villegas et al., 2016).本研究采用AIC进行模型选择,类别个数为Q时其表达式为:
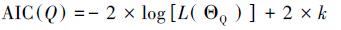
|
(7) |
式中,ΘQ表示类别个数为Q时模型参数集,L(ΘQ)为对应的似然函数,表征模型的拟合效果;k为参数个数,表征模型的复杂度.在层次聚类过程中,可分别计算类别个数从P-1到1时的AIC;此外,还需建立未进行聚类时的LMM并计算AIC(P).进一步,采用赤池权重(Akaike Weights)确定不同模型的相对重要性:首先计算不同模型的AIC相对于最小AIC的差值(式(8)),然后根据差值确定模型对应的权重(式(9))(Anderson and Burnham, 2002).

|
(8) |
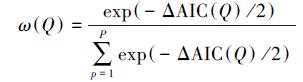
|
(9) |
式中,AICmin为AIC的最小值,ω(Q)为类别个数为Q的模型对应的赤池权重;赤池权重表示观测数据对备选模型的支持程度,全部备选模型的赤池权重之和为1,赤池权重越大则对应模型被选为最佳模型的可能性越大.本研究中LMM及线性回归模型的建立和实现全部基于R软件(Version 3.4.2).其中,LMM模型基于lme4软件包(Bates et al., 2015),在计算AIC时采用极大似然法(ML)进行参数估计以获得AIC值,在筛选出最佳类别个数后采用限制性极大似然法(REML)对筛选出的模型重新进行参数估计,以获得无偏估计(Hofmeister et al., 2015).
3 结果(Results) 3.1 层次聚类RCA的每次聚类均基于上一次的聚类状态,将且仅将2个类别聚为新类,因而具有层次结构.以云贵湖区Chla-TN关系的聚类(图 3a)为例,第1次聚类将洱海和杞麓湖聚为一类,此时的聚类状态为L4 = [(洱海, 杞麓湖), (阳宗海), (星云湖), (异龙湖)];第2次聚类则在L4的基础上,将(洱海, 杞麓湖)和(阳宗海)聚为一类L3 = [(洱海, 杞麓湖, 阳宗海), (星云湖), (异龙湖)].由于本研究中两个生态分区的两组响应关系均恰有5个湖泊,因而均在进行4次聚类之后完成聚类过程(图 3, 数字为聚类次数).该聚类结果直观地展示了层次聚类过程,体现了不同湖泊响应关系的相似性,与传统的仅基于监测数据的聚类有显著不同.
 |
| 图 3 层次聚类结果 Fig. 3 Hierarchical custering results |
根据不同类别个数对应的聚类状态建立相应的压力响应模型,即可计算AIC,进行模型选择(表 1).由结果可知,对于Chla-TN关系,两个生态分区最小AIC值对应的类别个数均为湖泊个数,即无需对响应关系进行任何聚类;对于Chla-TP关系,两个生态分区最小AIC值对应的类别个数均比湖泊个数小1,即需对湖泊进行一次聚类;而当类别个数为1时建立的区域性模型(式(6))对应的AIC均为最大.根据AIC值可得到模型的相对权重,4组响应关系的最小AIC值对应模型的权重分别为0.998、0.682、0.798和0.634,均大于0.6;而当类别个数为1时,建立的区域性模型对应的模型权重均小于0.001(表 1).
| 表 1 AIC、ΔAIC和ω结果 Table 1 Results of AIC, ΔAIC and ω |
选择最小AIC对应的模型为描述4组响应关系的最佳模型(表 1, 下划线数字),并与区域性响应关系进行对比,发现最佳模型的各个类别对应的响应关系大部分与区域性响应关系存在较大差异(图 4),区域性响应关系用于描述生态分区内某些湖泊的响应关系可能是不精确的.对于东部湖区的Chla-TN和Chla-TP关系,区域性响应关系的斜率低于最佳模型的各个类别对应的响应关系的斜率(图 4b和4 d);在对数线性模型中,斜率表征营养盐浓度升高/降低1%,对应的Chla浓度升高/降低的百分比(Qian, 2016);因而在这两组响应关系中,区域性响应关系低估了全部湖泊的营养盐对Chla的效应.此现象在生态学研究中被称为生态谬误(Ecological Fallacy)(Maas-Hebner et al., 2015).生态谬误描述的集合水平的响应关系不能用于推导个体水平响应关系的现象,反之亦然.生态谬误的出现表明,采用区域性响应关系来描述各个湖泊的响应关系时存在适应性的问题.
 |
| 图 4 区域响应关系与最佳模型各类别响应关系对比 Fig. 4 Comparisons of the Ecoregional and Cluster-specific Chla-nutrient Relationships |
传统的区域性营养盐基准的制定过程在空间尺度的确定和浓度限值的推导两个方面均存在缺陷,不能保证区域性营养盐基准的适用性.在空间尺度的确定方面,采用自上而下的思路将大陆整体划分为生态分区,划分的依据多为大尺度的驱动因子(如气候、植被覆盖、地质)(Huo et al., 2014; Omernik and Griffith, 2014).然而,这些大尺度因子与营养盐基准之间是否存在因果关系缺乏科学论证;实际上,很多生态分区划分的初衷并非为建立区域性营养盐基准(Cheruvelil et al., 2013),因而划分生态分区并不能保证区域性湖泊营养盐基准的适用性.此外,在对生态系统的认知不全面的条件下,难以对营养盐基准有影响的驱动因子全部列出(Hamil et al., 2016),无法判断未被列出的驱动因子是否会影响区域性营养盐基准的适用性.在浓度限值的推导方面,由于缺乏长时间水质数据,很多研究采用空间换时间的策略,将区域内大量湖泊的监测数据聚集起来建立模型(Phillips et al., 2008; Yuan and Pollard, 2015),而未对空间换时间策略的合理性进行验证.近年来,注意到变量之间的响应关系在时间和空间上变化可能是非同步的,很多生态学研究已质疑空间换时间策略的合理性(Huang et al., 2017; Mimet et al., 2016; Roitberg and Shoshany, 2017).
在本研究中,驱动因子的空间异质性被视为潜变量,采用LMM的随机效应项表示,克服了驱动因子难以全部列举的问题(Hamil et al., 2016);采用长时间水质数据,避免使用空间换时间策略.本研究提出的RCA提供了一种自下而上地探究营养盐基准空间尺度的思路;基于RCA的结果,本研究发现区域性响应关系不能准确甚至不能正确地模拟生态分区内某些湖泊Chla与营养盐的响应关系,区域性响应关系对应的模型权重极小,表明生态分区内局部驱动因子对响应关系有较大影响,而区域性营养盐基准不能适用于生态分区内的全部湖泊.探究生态分区内响应关系差异的驱动因子对于湖泊富营养化控制具有重要意义(Soranno et al., 2014),本研究受限于湖泊个数较少而未进行相关分析.
4.2 基于RCA的浓度限值推导RCA能够识别出用于模拟区域营养盐与管理终点的响应关系的最佳压力响应模型,提高浓度限值推导的准确性;在给定管理终点的目标值时,根据该压力响应模型即可推导各个类别对应的营养盐浓度限值,并进一步地得到每个湖泊的营养盐基准.需要指出的是,本研究所用的RCA虽然可对最佳响应关系进行识别,却未穷举P个湖泊进行聚类的全部可能聚类状态,因而得到的最佳模型可能是“局部”最佳模型.在层次聚类过程中,建立的压力响应模型个数为CP2+CP-12+, …, +C22=CP+13.本研究中P均为5,模型个数均为20.若穷举全部可能组合,则需建立的压力响应模型个数为湖泊个数P对应的贝尔数(BP, Bell Number)(Klazar, 2003):
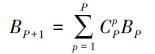
|
(10) |
式中,B0= 1.当P = 5时,B5= 52;而当P = 8时,B8高达4140.显然,当湖泊个数增加时,穷举全部组合面临着计算效率的挑战.本研究旨在探究区域性营养盐基准的适应性,采用层次聚类模型即可满足探索需求.进一步地,欲确保筛选的最佳模型为“全局”最佳,则需探索合理的方法克服全部穷举带来的计算效率问题.此外,对于氮、磷共限制的湖泊,建立营养盐基准时还应考虑二者的协同效应(Malve and Qian, 2006).
5 结论(Conclusions)1) 为探究区域性湖泊营养盐基准的适用性,本研究提出一种包括层次聚类过程和模型选择过程的RCA,并将该方法应用于云贵湖区和东部湖区Chla与营养盐响应关系的聚类中.研究结果表明区域性湖泊营养盐基准不能适用于生态分区内的全部湖泊.
2) 探究生态分区内响应关系差异的驱动因子,对于区域水污染防治具有重要意义;随着监测数据的积累,可在RCA结果的基础上进一步地识别驱动因子,提高污染防治的针对性和有效性.
3) 本研究提出的RCA具有直观快捷的特点;本研究给出了RCA的具体步骤,然而RCA的实现过程中,在聚类思路、压力响应模型形式、模型拟合效果统计量、模型选择准则等方面均具有较大的灵活性,可根据应用需求进行选择,方便地应用于其它需要对响应关系进行聚类的研究中.
4) 当前,我国正在积极推进区域性营养盐基准的建立工作,本研究对区域性湖泊营养盐基准适用性的探讨以及提出的RCA,可为我国湖泊营养盐基准制定的空间尺度和浓度限值提供参考.
Altman N, Krzywinski M. 2017. Clustering[J]. Nature Methods, 14: 545–546.
DOI:10.1038/nmeth.4299
|
Anderson D R, Burnham K P. 2002. Avoiding pitfalls when using information-theoretic methods[J]. Journal of Wildlife Management, 66: 912–918.
DOI:10.2307/3803155
|
Barrero M A, Orza J A G, Cabello M, et al. 2015. Categorisation of air quality monitoring stations by evaluation of PM10 variability[J]. Science of the Total Environment, 524: 225–236.
|
Bates D, MaeChler M, Bolker B M, et al. 2015. Fitting linear mixed-effects models using lme4[J]. Journal of Statistical Software, 67: 1–48.
|
Bennett N D, Croke B F W, Guariso G, et al. 2013. Characterising performance of environmental models[J]. Environmental Modelling & Software, 40: 1–20.
|
Chen L, Li S, Wang G, et al. 2017. Validation of the Soil and Water Assessment Tool (SWAT) in ungauged catchment[J]. Journal of Environmental Accounting and Management, 5(3): 233–242.
DOI:10.5890/JEAM.2017.09.005
|
Cheruvelil K S, Soranno P A, Webster K E, et al. 2013. Multi-scaled drivers of ecosystem state:quantifying the importance of the regional spatial scale[J]. Ecological Applications, 23(7): 1603–1618.
DOI:10.1890/12-1872.1
|
Conley D J, Paerl H W, Howarth W, et al. 2009. Controlling eutrophication:Nitrogen and phosphorus[J]. Science, 323(5917): 1014–1015.
DOI:10.1126/science.1167755
|
Dodds W K K, Welch E B. 2000. Establishing nutrient criteria in streams[J]. Journal of the North American Benthological Society, 19(1): 186–196.
DOI:10.2307/1468291
|
Evans-White M A, Haggard B E, Scott J T. 2013. A review of stream nutrient criteria development in the United States[J]. Journal of Environmental Quality, 42(4): 1002–1014.
DOI:10.2134/jeq2012.0491
|
Fergus C E, Soranno P A, Cheruvelil K S, et al. 2011. Multiscale landscape and wetland drivers of lake total phosphorus and water color[J]. Limnology & Oceanography, 56(6): 2127–2146.
|
Hamil K A D, Iii B V I, Huang W K, et al. 2016. Cross-scale contradictions in ecological relationships[J]. Landscape Ecology, 31(1): 7–18.
DOI:10.1007/s10980-015-0288-z
|
Han D, Currell M J, Cao G. 2016. Deep challenges for China's war on water pollution[J]. Environmental Pollution, 218: 1222–1233.
DOI:10.1016/j.envpol.2016.08.078
|
Heiskary S A, Bouchard R W Jr. 2015. Development of eutrophication criteria for Minnesota streams and rivers using multiple lines of evidence[J]. Freshwater Science, 34(2): 574–592.
DOI:10.1086/680662
|
Hofmeister J, Hošek J, Brabec M, et al. 2015. Value of old forest attributes related to cryptogam species richness in temperate forests:A quantitative assessment[J]. Ecological Indicators, 57: 497–504.
DOI:10.1016/j.ecolind.2015.05.015
|
Huang M, Piao S, Janssens I A, et al. 2017. Velocity of change in vegetation productivity over northern high latitudes[J]. Nature Ecology & Evolution, 1(11): 1649–1654.
|
Huo S, Ma C, Xi B, et al. 2014. Lake ecoregions and nutrient criteria development in China[J]. Ecological Indicators, 46: 1–10.
DOI:10.1016/j.ecolind.2014.06.014
|
Huo S, Ma C, Xi B, et al. 2017. Development of methods for establishing nutrient criteria in lakes and reservoirs:A review[J]. Journal of Environmental Sciences, 67: 54–56.
|
Huo S, Xi B, Ma C, et al. 2013. Stressor-Response Models:A practical application for the development of lake nutrient criteria in China[J]. Environmental Science & Technology, 47: 11922–11923.
|
Ingrassia S, McLaChlan G J, Govaert G. 2015. Special issue on "New trends on model-based clustering and classification"[J]. Advances in Data Analysis and Classification, 9: 367–369.
DOI:10.1007/s11634-015-0224-8
|
Kim S. 2015. ppcor:An R Package for a Fast Calculation to Semi-partial Correlation Coefficients[J]. Communications for Statistical Applications and Methods, 22(6): 665–674.
DOI:10.5351/CSAM.2015.22.6.665
|
Klazar M. 2003. Bell numbers, their relatives, and algebraic differential equations[J]. Journal of Combinatorial Theory Series A, 102(1): 63–87.
DOI:10.1016/S0097-3165(03)00014-1
|
Le C, Zha Y, Li Y, et al. 2010. Eutrophication of Lake Waters in China:Cost, Causes, and Control[J]. Environmental Management, 45(4): 662–668.
DOI:10.1007/s00267-010-9440-3
|
梁中耀, 刘永, 盛虎, 等. 2014. 滇池水质时间序列变化趋势识别及特征分析[J]. 环境科学学报, 2014, 34(3): 754–762.
|
Liu Z, Zhu Y, Li F, et al. 2017. Non-destructively predicting leaf area, leaf mass and specific leaf area based on a linear mixed-effect model for broadleaf species[J]. Ecological Indicators, 78: 340–350.
DOI:10.1016/j.ecolind.2017.03.025
|
Maas-Hebner K G, Harte M J, Molina N, et al. 2015. Combining and aggregating environmental data for status and trend assessments:challenges and approaches[J]. Environmental Monitoring & Assessment, 187(5): 278.
|
Malve O, Qian S S. 2006. Estimating nutrients and Chlorophyll a relationships in Finnish lakes[J]. Environmental Science & Technology, 40(24): 7848–7853.
|
Mclaughlin D B. 2014. Maximizing the accuracy of field-derived numeric nutrient criteria in water quality regulations[J]. Integrated Environmental Assessment & Management, 10(1): 133–137.
|
McLaughlin D B, Reckhow K H. 2017. A Bayesian network assessment of macroinvertebrate responses to nutrients and other factors in streams of the Eastern Corn Belt Plains, Ohio, USA[J]. Ecological Modelling, 345: 21–29.
DOI:10.1016/j.ecolmodel.2016.12.004
|
Mimet A, Pellissier V, Houet T, et al. 2016. A holistic landscape description reveals that landscape configuration changes more over time than composition:Implications for landscape ecology studies[J]. Plos One, 11(3): e0150111.
DOI:10.1371/journal.pone.0150111
|
Murtagh F, Contreras P. 2017. Algorithms for hierarchical clustering:an overview, Ⅱ[J]. Data Mining and Knowledge Discovery, 2(1): 86–97.
|
Oliver S K, Collins S M, Soranno P A, et al. 2017. Unexpected stasis in a changing world:Lake nutrient and Chlorophyll trends since 1990[J]. Global Change Biology, 23(12): 5455–5467.
DOI:10.1111/gcb.2017.23.issue-12
|
Olson J R, Hawkins C P. 2013. Developing site-specific nutrient criteria from empirical models[J]. Freshwater Science, 32(3): 719–740.
DOI:10.1899/12-113.1
|
Omernik J M, Griffith G E. 2014. Ecoregions of the conterminous United States:Evolution of a hierarchical spatial framework[J]. Environmental Management, 54(6): 1249–1266.
DOI:10.1007/s00267-014-0364-1
|
Phillips G, Pietiläinen O P, Carvalho L, et al. 2008. Chlorophyll-nutrient relationships of different lake types using a large European dataset[J]. Aquatic Ecology, 42(2): 213–226.
DOI:10.1007/s10452-008-9180-0
|
Piou C, Berger U, Grimm V. 2009. Proposing an information criterion for individual-based models developed in a pattern-oriented modelling framework[J]. Ecological Modelling, 220(17): 1957–1967.
DOI:10.1016/j.ecolmodel.2009.05.003
|
Qian S S. 2010. Environmental and Ecological Statistics with R[M]//Environmental and ecological statistics with R/. Chapman & Hall/CRC. 117-154
|
Qian S S, Stow C A, Cha Y. 2015. Implications of Stein's Paradox for environmental standard compliance assessment[J]. Environmental Science & Technology, 49(24): 5913–5920.
|
Read E K, Patil V P, Oliver S K, et al. 2015. The importance of lake-specific characteristics for water quality across the continental United States[J]. Ecological Applications, 25(4): 943–955.
DOI:10.1890/14-0935.1
|
Rohm C M, Omernik J M, Woods A J, et al. 2002. Regional characteristics of nutrient concentrations in streams and their application to nutrient criteria development[J]. Journal of the American Water Resources Association, 38(1): 213–239.
DOI:10.1111/jawr.2002.38.issue-1
|
Roitberg E, Shoshany M. 2017. Can spatial patterns along climatic gradients predict ecosystem responses to climate change? Experimenting with reaction-diffusion simulations[J]. Plos One, 12(4): e0174942.
DOI:10.1371/journal.pone.0174942
|
Soranno P A, Cheruvelil K S, Bissell E G, et al. 2014. Cross-scale interactions:quantifying multi-scaled cause effect relationships in macrosystems[J]. Frontiers in Ecology & the Environment, 12(1): 65–73.
|
Stoddard J L. 2004. Use of ecological regions in aquatic assessments of ecological condition[J]. Environmental Management, 34: S61–S70.
DOI:10.1007/s00267-003-0193-0
|
Tuckey J W. 1977. Exploratory Data Analysis[M]. Addison-Wesley Pub. Co: 163–182.
|
US EPA. 1998. National Strategy For The Development Of Regional Nutrient Criteria. EPA-822-R-98-002[R]. US EPA, Office of Water, Washington, D. C., USA
|
Villegas M, Newsome S D, Blake J G. 2016. Seasonal patterns in delta H-2 values of multiple tissues from Andean birds provide insights into elevational migration[J]. Ecological Applications, 26(8): 2381–2387.
|
Wagner T, Soranno P A, Webster K E, et al. 2011. Landscape drivers of regional variation in the relationship between total phosphorus and Chlorophyll in lakes[J]. Freshwater Biology, 56(9): 1811–1824.
DOI:10.1111/fwb.2011.56.issue-9
|
Xu H, Paerl H W, Qin B, et al. 2015. Determining critical nutrient thresholds needed to control harmful cyanobacterial blooms in eutrophic lake taihu, China[J]. Environmental Science & Technology, 49(2): 1051–1059.
|
Yuan L L, Pollard A I. 2015. Deriving nutrient targets to prevent excessive cyanobacterial densities in US lakes and reservoirs[J]. Freshwater Biology, 60(9): 1901–1916.
DOI:10.1111/fwb.12620
|
Zhang Y, Huo S, Ma C, et al. 2014. Using stressor-response models to derive numeric nutrient criteria for lakes in the eastern plain ecoregion, China[J]. Clean-Soil Air Water, 42(11): 1509–1517.
DOI:10.1002/clen.201300708
|
 2018, Vol. 38
2018, Vol. 38


