环境科学学报  2018, Vol. 38 Issue (7): 2757-2763
引用本文
徐光平, 王嘉松. 2018. 基于非圆球模式的大气超细颗粒物在沉积和凝并共同作用下的动力学模型研究[J]. 环境科学学报, 38(7): 2757-2763.
Xu G P, Wang J S. 2018. Research on dynamic model of non-spherical ultrafine particles considering both deposition and coagulation[J]. Acta Scientiae Circumstantiae, 38(7): 2757-2763.
基于非圆球模式的大气超细颗粒物在沉积和凝并共同作用下的动力学模型研究    [PDF全文]
徐光平 , 王嘉松     
上海交通大学, 船舶海洋与建筑工程学院, 工程力学系, 上海 200240
收稿日期: 2017-12-19; 修回日期: 2018-02-02; 录用日期: 2018-02-02
作者简介: 徐光平(1987-), 男, 博士研究生, E-mail:xgp19870409@126.com
通讯作者（责任作者）: 王嘉松, E-mail:jswang@sjtu.edu.cn
摘要: 数值模拟了封闭环境内非球形超细颗粒物的动力学演化，以探讨颗粒物的沉积和凝并行为.采用泰勒展开方法导出了描述颗粒物动力学这两种行为共同作用的矩方程.通过与实验结果对比表明：本文得出的矩方程相对于传统的矩方程模型更适于刻画颗粒物的扩散和重力沉积，能够精确地预测它们的动力学演变过程.通过将颗粒形状参数（分形维数，Df）纳入原始动力学方程，使得颗粒物凝并模型可以较为准确地描述真实情况下非球形颗粒的凝并行为.此外在高颗粒物浓度条件下，得出颗粒物的演变主要受到凝并作用的影响，沉积作用则相对较弱.
关键词: 非圆球模式     超细颗粒     沉积     凝并     矩方法    
Research on dynamic model of non-spherical ultrafine particles considering both deposition and coagulation
XU Guangping, WANG Jiasong    
Department of Engineering Mechanics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240
Received 19 December 2017; received in revised from 2 February 2018; accepted 2 February 2018
Biography: XU Guangping(1987—), male, Ph.D. candidate, E-mail: xgp19870409@126.com
*Corresponding author: WANG Jiasong, E-mail: jswang@sjtu.edu.cn
Abstract: This paper numerically investigates a dynamical evolution of ultrafine nonspherical particles in closed environments so as to explore their deposition and coagulation processes. The moment equations describing the dynamical behavior together considering both of above processes of the particles are derived from the Taylor expansion. Numerical results show that by comparing with the experimental data, the current equations are more suitable than the traditional ones to describe the diffusion and deposition of these particles and can accurately predict their dynamical evolution process. The coagulation model proposed in the paper is able to precisely describe coagulative behaviors of those nonspherical particles due to introduction of fractal dimension (Df) of the particles to the dynamical equations. In addition, in the case of high particle concentration, the particle evolution is mainly affected by the coagulation rather than the deposition.
Key words: non-spherical mode     ultrafine particle     deposition     coagulation     moment method    
1 引言(Introduction)

雾霾现象已成为当今社会最为关注及亟待解决的环境问题之一(刘强等, 2014; Sun et al., 2016).细颗粒物(直径小于2.5 μm)和超细颗粒物(直径小于1.0 μm)大量存在于空气中是导致这一现象的直接原因.相比于对城市大尺度环境造成污染, 这些颗粒物对室内等小尺度环境的影响则尤为受到关注(Grau-Bové et al., 2013; Chu et al., 2017).当人们长时间处于较差通风条件下的室内环境中, 空气中的悬浮颗粒物则很容易通过呼吸道进入人体肺部并粘附堆积, 对身体健康造成严重的影响(Gens et al., 2014; Othman et al., 2016).因此, 室内环境的质量与人体健康之间的关系更为密切, 有必要对室内颗粒物的演化机理进行深入的研究.

在绝大部分室内环境中, 沉积和凝并行为对悬浮颗粒物随时空的变化过程起着主要的作用.Hussein等(2009)的实验研究表明, 当颗粒浓度小于3×103 cm-3时, 可以不考虑凝并效应对颗粒浓度变化的影响, 而如果大于104 cm-3, 凝并和沉积行为都对颗粒物的演化起着重要的作用.同时, 已有的针对室内条件下的颗粒物研究通常是考虑单一动力学行为下进行的(Chen et al., 2016; 杨曼丽等, 2016), 因此有必要对多种动力学行为共同作用下颗粒物的演化规律进行深入的研究.传统矩方法(Method of moment, MOM)是目前常用的一种用来处理超细颗粒物动力学问题的数学方法, 如Park等(2002)应用此方法模拟求解了颗粒的沉积问题, 但这种假设对于非对数正态分布的颗粒而言则不适用, 很大程度上限制了方程的实际应用性.此外, 目前关于凝并行为下的数值模拟研究主要基于颗粒为圆球模式的前提下开展的(Veshchunov, 2015; Polovnikov et al., 2016), 而实际情况下绝大多数种类的颗粒表现为不规则形状, 这使得理论研究结果与实际情况存在着一定的差异性, 因此针对这一问题有必要进行进一步的理论研究.

本文应用泰勒展开矩方法(Taylor-expansion method of moment, TEMOM), 将其扩展应用到考虑沉积动力学行为下的颗粒物动力学平衡方程中, 同时将颗粒的分形维数纳入颗粒凝并的动力学模型中, 导出了颗粒在沉积和凝并两种行为共同作用下的矩方程模型.通过与已有的室内颗粒扩散实验结果进行对比, 模拟了室内封闭环境内颗粒物在凝并和沉积的共同作用下, 总颗粒数量、平均粒径大小及颗粒尺度分布随时间的变化过程, 分析了颗粒实际形状在颗粒演化过程中对颗粒数量浓度的影响程度.

2 数学模型(Mathematical model)

矩方法是目前常用的一种处理颗粒物动力学方程的方法.此方法通过定义各阶矩值来间接对颗粒物的平均量和统计量进行描述, 包括颗粒的数量浓度、体积(质量)浓度、空间内的分散程度及平均尺度等, 进而给出整个颗粒群的动力学演变过程.

泰勒展开矩方法是基于传统矩方法发展而来的一种新的求解动力学方程的数学方法(Yu et al., 2008).传统矩方法需要预先假设颗粒物的初始分布, 从而限制了应用范围.而泰勒展开的矩方法对于颗粒的初始分布没有任何数学上的限制, 同时, Yu等(2017)应用此方法在颗粒物的布朗凝并问题上进行了详细的论证, 结果表明此方法在计算精度、计算效率上都有了很大的提高.因此, 本文将此方法进一步扩展到颗粒的沉积和基于非圆球模式下的凝并问题中, 对其准确性进行了对比验证.

欧拉坐标系下, 考虑凝并和沉积共同作用下的颗粒尺度分布函数的通用动力学方程如下(Matsoukas et al., 1991)：

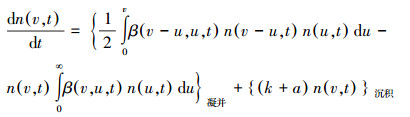
(1)

式中, n(v, t)表示颗粒尺度分布函数；n(v, t)dv表示t时刻, 尺度范围在v~v+dv内的颗粒在单位体积内的数量浓度；β(u, v, t)是尺度分别为u, v的两个颗粒的凝并核函数, 表示两颗粒发生一次凝并的概率；k为颗粒的沉积系数；a为空气交换率(通风率).

在无任何假设的前提下, 目前式(1)并没有相对应的理论解, 因此需要应用适当的方法对其转化成可求解的形式.其中需要用到矩的定义如下：

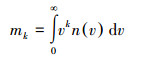
(2)

在Stokes-Einstein理论框架内, 复杂的凝并核模型β(u, v, t)会使式(1)难以自动封闭, 所以对于凝并核函数的处理至关重要(这里认为一般情况下两颗粒碰撞即发生凝并, 也即碰撞核=凝并核).根据颗粒的努森(Kn=2λ/D, λ为气体分子的平均自由程, D为颗粒的动力学直径)数的大小可以大致分为自由分子区和连续区, 不同区内的β(u, v, t)具有各自的动力学模型表达式, 下面分别进行描述.

2.1 凝并模型

考虑颗粒分形维数的自由分子区凝并核的表达式如下(Mountain et al., 1986)：

(3)

式中, B1=(3/4π)1/6(6kbT/ρ)1/2r02(1－3/Df), kb为玻尔兹曼常数, T为气体温度, ρ为颗粒密度, Df为颗粒的分形维数, 反映颗粒的实际形状.考虑Df的连续区的凝并核表达式如下(Mountain et al., 1986).

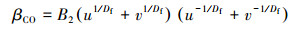
(4)

式中, B2=3kbT/2μ, μ为气体的动力粘度.当Df=3.0时, 代表颗粒凝并为典型的圆球模式.Yu等(2008)已经应用泰勒展开方法对基于此模式下的凝并方程进行了深入研究.本文将Df作为变量处理, 重新推导能够适用于不同实际形状颗粒的凝并模型.通过式(2)可以将式(1)中的凝并项转化成矩方程的形式, 但转化后的数学方程中仍然存在分数项形式的矩变量, 仍无法直接求解, 因此这里应用泰勒展开方法, 在v=a处进行泰勒级数展开得到(Yu et al., 2008)：

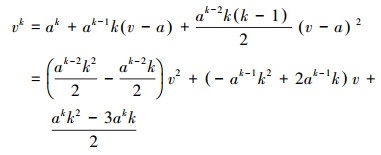
(5)

将式(2)代入到式(5)中得：

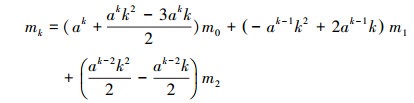
(6)

此时, 利用式(6)就可以消掉矩方程中的非整数矩项, 推导出在非圆球模式下颗粒凝并的矩方程模型(7)和(8)如下.

自由分子区：

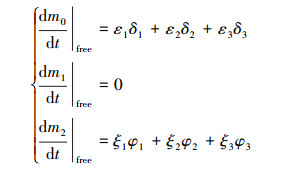
(7)

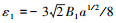
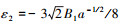
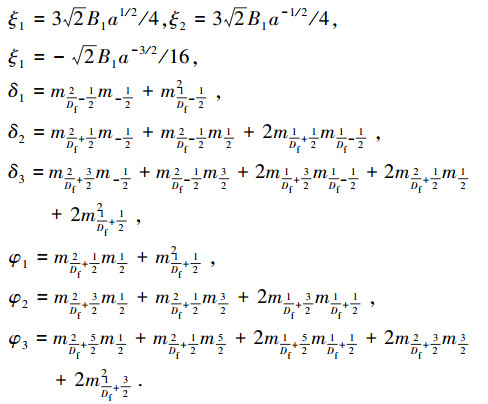
其中, , , ε3=,

连续区：

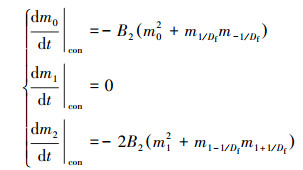
(8)

描述全区间尺度颗粒凝并的矩方程表达式的方法主要有调和平均和Otto平均处理, 前人对这两种方法进行了比较研究, 得出的结论是Otto法所计算出结果的精确度更高(Otto et al., 1999), 因此这里采用了此方法进行处理.Otto方法的数学表达式如下：

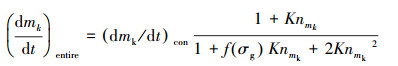
(9)

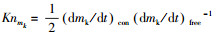
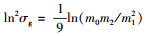
其中, , f(σg)=2+0.7ln2σg+0.85ln3σg, , 将式(7)与式(8)结合, 就可以得到全区间尺度范围内颗粒物的凝并动力学模型.

2.2 沉积模型

颗粒物的原始沉积核模型如下(Park et al., 2002).

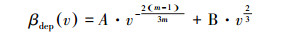
(10)

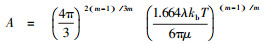
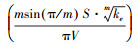
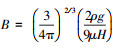
其中, , , v为颗粒的体积, λ表示气体分子的平均自由程, S表示计算域的总表面积, H表示计算域的高度, V表示计算域的总体积, m为已知位于2~3之间的一个经验常数, 这里与文献中取值保持一致, 取值为2.6.由于颗粒的沉积属于单颗粒动力学行为, 只受到颗粒扩散作用的影响, 并不涉及颗粒之间的相互作用, 不会对颗粒的演化过程产生影响, 因此这里仍然可以按照圆球颗粒模式来处理.

同样应用式(2)的矩定义, 可以将式(10)转换成矩方程的形式：

(11)

传统矩模型(Method of moment, MOM)对式(11)中的分数矩项利用初始浓度分布为初始对数正态分布来处理,

再次利用泰勒展开将式(11)中含有的非整数矩消掉, 得到最终的需要数值求解的方程如下:

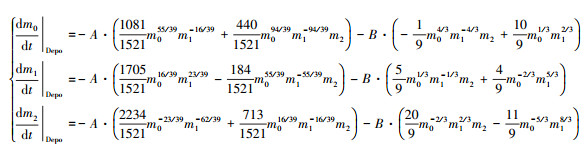
(12)
3 数值方法验证与分析(Numerical method validation and analysis) 3.1 颗粒物在沉积动力学行为下的数值模拟结果验证

为了验证应用泰勒展开方法所推导出的沉积模型的可靠性, 这里分别应用基于传统矩方法(MOM)和泰勒展开方法(TEMOM)所建立的模型进行数值求解并与孙在等(2007)的实验结果进行对比(图 1).整个实验区域为一长方体模拟室, 长×宽×高为0.78 m×1.17 m×1.17 m.通过蜡烛燃烧产生气溶胶颗粒, 其初始数量浓度(N)为2.11×105 cm-3, CMD(Count Median Diameter, 数量中位径)为32.2 nm, GSD (Geometric Standard Deviation, 几何标准差)为2.42.模拟初始参数与实验值保持一致, 前三阶矩方程采用四阶Runge-Kutta法进行求解, 时间步长取0.1 s, 计算总时长为60 min.

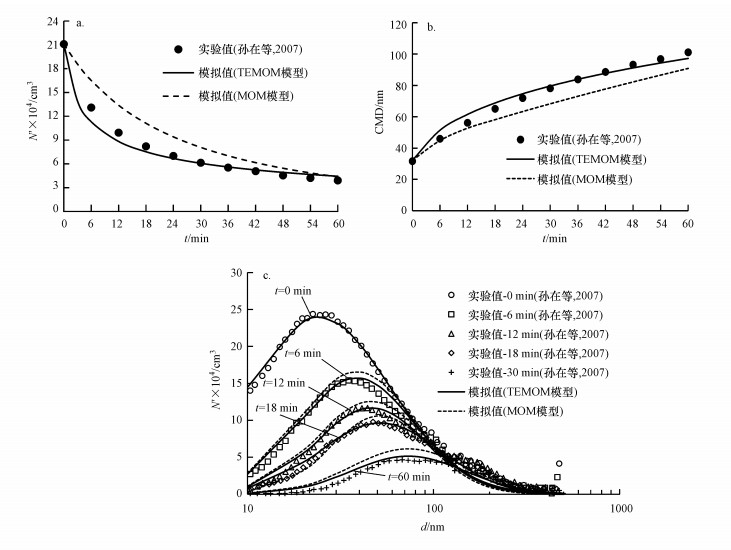图 1 实验值与模拟值得到的颗粒数量浓度对比(a), CMD (数量中位径)对比(b)及PSD (颗粒尺度分布)对比(c) Fig. 1 Comparison of temporal total number concentration(a), particle CMD (Count Median Diameter) (b) and the PSD (Particle Size Distribution) between experiment and simulation(c)

图 1a为两种计算方法下颗粒总数量浓度的变化与实验值的对比结果, 图中的纵坐标N′=dN/dlogd.由于沉积效应的作用, 使得空间内的颗粒总数量随时间逐渐减少.在颗粒演化的初始阶段, 两种方法的模拟结果差异较为明显, 随着时间的推移, 二者之间的差异越来越小, 最后阶段二者的浓度值几乎重合.同时, TEMOM模型得到的结果与实验值更为接近.图 1b表示两种方法得到的CMD与实验结果的比较, 扩散和重力两种沉积模式共同作用使得颗粒的平均粒径逐渐增大.同样地, 应用TEMOM模型得到的结果与实验值之间的差异更小.图 1c对比了4个不同时刻下的PSD与实验结果之间的一致性.可以看出, TEMOM模型下的模拟结果虽在局部有些差异, 但相对而言仍然与实验值更为吻合.而MOM模型计算得到的PSD峰值明显要比实验值大, 并且随时间变化过程中, 这种差异性表现得更为明显.从数学方法的角度看, MOM方法是在有颗粒初始分布形态假设的前提下得到的, 这使得原始模型本身存在一定的模型误差, 而TEMOM方法在处理分数矩项时, 是没有在假设任何颗粒初始浓度分布的前提下进行推导的, 因此消除了数学模型假设的误差, 使其计算精度和适用范围均得到了提高.对比结果同时也表明, 应用前三阶矩下的泰勒展开方法本身存在的截断误差对精度的影响远小于数学上的模型假设误差.通过以上对比结果可以得出, 应用TEMOM方法建立的关于颗粒沉积作用的矩方程模型在适用性得到提高的同时, 也能够更为准确地预测室内环境下颗粒物的演化过程.

3.2 同时考虑颗粒物凝并和沉积的动力学模型模拟结果

为了验证改进后的动力学模型的准确性, 本文分别选取高浓度环境和中等浓度环境下颗粒的演化过程与实验进行对比(图 2).针对高浓度环境(颗粒的总数量浓度为1.0×106 cm-3), 将计算结果与Kim等(2006)中的实验结果进行对比, 计算参数与文献中的实验参数保持一致.在进行高浓度条件下的实验之前, 为了分析沉积和凝并两种作用对颗粒演化的影响程度, 在相同实验条件下, 文献中首先设计了低浓度初始环境下(1.0×103 cm-3)的实验工况.此种条件下可以忽略凝并行为对颗粒的影响, 只有沉积作用影响颗粒的演化过程.颗粒数量浓度通过粒子计数器(型号：CPC, TSI model 3022)测得, 每隔12 min采取1次数据.实验几何模型为圆柱形箱体, 底面直径为60 cm, 高为60 cm.颗粒为氯化钠固态颗粒, 其密度为2.16 g·cm-3, 分形维数在2.1~2.5之间波动(Horne, 1987), 本文选取平均值Df =2.3作为计算参数.t=0时刻, 几何平均直径为50 nm, 几何标准差为1.6, 选取时间步长为0.1 s, 计算时间为2000 s.

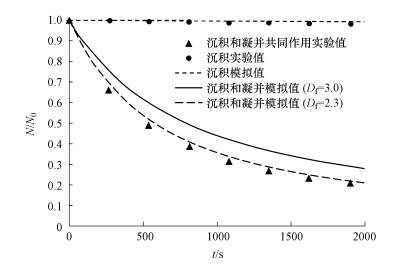图 2 高浓度环境下颗粒的总数量浓度的实验值和模拟值随时间的变化对比 Fig. 2 Comparison between measured and simulated values of particle number concentration varying with time under high concentration condition

从图 2的对比结果中可以看到, 描述沉积情况下的实验值和模拟值相差很小, 而对于颗粒凝并的情况下, 颗粒的总数量均呈现减小的趋势, 但二者的结果差异较大, 模拟结果大于实验测量值.从模拟的前2000 s的时间内可以看出, 颗粒沉积作用下, 总数量浓度下降很小, 而较高的初始浓度条件下, 颗粒的凝并作用使得颗粒总数量浓度迅速下降, 凝并占据了主导地位.这是由于所给定颗粒的初始浓度相对较高, 颗粒之间发生碰撞凝并的动力学行为的概率更高.而颗粒的初始几何平均直径较小, 颗粒在扩散和重力作用下, 其沉积行为所经历的时间要更长, 因此在较短的模拟计算时间内, 颗粒的数量浓度并没有明显的减少.在圆球模式下, 颗粒沉积的模拟结果与实验值相比偏大.应用非圆球模式下的矩方程模型所得的模拟结果与实验值吻合地很好.从微观角度看, 相对于圆球状颗粒, 具有不规则微观形状的颗粒之间碰撞时会增加相应的接触面积, 因而使得颗粒凝并的概率得到提高, 颗粒数量浓度下降得也越快.

图 3为中等浓度条件下(颗粒的总数量浓度N0为1.4×104 cm-3), 颗粒数量浓度N随时间的变化曲线.这里将数值模拟结果与Naumann (2003)的实验结果进行对比验证, 实验环境为一圆柱形空间, 体积为84.3 m3, 释放的颗粒为柴油烟颗粒(Df≈2.1), 密度1.7 g·cm-3, 直径473 nm.从图中可以看出, 相比于图 2, 由于颗粒初始浓度较低, 其数量浓度随时间的减少非常缓慢, 整个过程持续2700 min.与图 2的对比结果类似, 采用非圆球模式下的动力学方程模拟得到的数量浓度变化与实验值更为接近, 模拟结果更为准确可靠.同时, 当仅考虑颗粒凝并作用下的模拟结果与同时考虑凝并和沉积两种作用下的结果具有明显的差异, 这种差异性在图 2中高浓度环境下表现得非常微弱, 这说明颗粒的沉积作用相比高浓度条件下表现得更为明显, 当仅考虑颗粒凝并作用时, 模拟结果并不能准确反映颗粒数量随时间的实际变化情况, 这与高浓度环境下的演化过程差异明显.

图 3 中等浓度环境下颗粒的总数量浓度的实验值和模拟值随时间的变化对比 Fig. 3 Comparison between measured and simulated values of particle number concentration varying with time under medium concentration condition

图 2和图 3均表明, 颗粒形状对凝并作用有着非常重要的影响, 同时也证明了所建立的动力学模型能够很好地预测超细颗粒的数量浓度在凝并作用下的演化规律.相比较而言, 颗粒若只受沉积作用, 其演化规律并不受到颗粒形状的影响, 这也间接说明了图 2中沉积情况下的实验值和计算值相差很小的原因.相比较而言, 在一般中等浓度条件下, 颗粒的凝并和沉积作用均对颗粒的演化有着重要的影响, 而较高浓度环境下, 颗粒的凝并起着主导作用.综上所述, 为了更加准确描述颗粒浓度的演变过程, 本文将颗粒的真实形状影响考虑进描述凝并的数学模型中, 并与之将颗粒沉积作用相结合, 改进后的凝并模型能够更准确地描述颗粒的浓度变化特征, 进而在实际条件下有着更好的应用性.

4 结论(Conclusions)

1) 相较于传统矩方法, 应用泰勒展开方法建立的关于颗粒物沉积的动力学模型能够更为准确地预测室内环境中颗粒物在沉积作用下的数量浓度、平均粒径及颗粒尺度分布随时间的变化过程.此方法无需对颗粒的初始分布进行假设, 同时可以模拟具有不同实际形状的大气超细颗粒物, 其准确性和适用性均得到了很大的提高.

2) 相比于圆球模式, 非圆球模式下模拟得到的颗粒演化过程与实验值更为接近, 计算结果更为准确, 证明了颗粒的实际形状对颗粒的凝并行为有着及其重要的影响.所建立的非圆球模式下凝并模型更适于刻画实际形状颗粒物的动力学演变.

3) 中等浓度条件下, 颗粒的凝并和沉积均对颗粒的变化过程起着重要影响.随着初始浓度的提高, 凝并行为对颗粒物的演化影响程度逐渐增加, 相对而言, 沉积行为的影响程度则逐渐减弱.

参考文献
Chen C, Lin C H, Wei D, et al. 2016. Modeling particle deposition on the surfaces around a multi-slot diffuser[J]. Building & Environment, 107: 79–89.
Chu Y, Xu P, Yang Z, et al. 2017. Retrofitting existing buildings to control indoor PM2.5 concentration on smog days:Initial experience of residential buildings in China[J]. Building Services Engineering Research and Technology: 0143624417728187.
Gens A, Hurley J F, Tuomisto J T, et al. 2014. Health impacts due to personal exposure to fine particles caused by insulation of residential buildings in Europe[J]. Atmospheric Environment, 84(1): 213–221.
Grau-Bové J, Strlič M. 2013. Fine particulate matter in indoor cultural heritage:a literature review[J]. Heritage Science, 1(1): 8. DOI:10.1186/2050-7445-1-8
Horne D S. 1987. Determination of the fractal dimension using turbidimetric techniques. Application to aggregating protein systems[J]. Faraday Discussions of the Chemical Society, 83(1): 259–270.
Hussein T, Hruška A, Dohányosová P, et al. 2009. Deposition rates on smooth surfaces and coagulation of aerosol particles inside a test chamber[J]. Atmospheric Environment, 43(4): 905–914. DOI:10.1016/j.atmosenv.2008.10.059
Kim D S, Hong S B, Kim Y J, et al. 2006. Deposition and coagulation of polydisperse nanoparticles by Brownian motion and turbulence[J]. Journal of Aerosol Science, 37(12): 1781–1787. DOI:10.1016/j.jaerosci.2006.07.001
刘强, 李平. 2014. 大范围严重雾霾现象的成因分析与对策建议[J]. 中国社会科学院研究生院学报, 2014(5): 63–68.
Matsoukas T, Friedlander S K. 1991. Dynamics of aerosol agglomerate formation[J]. Journal of Colloid & Interface Science, 146(2): 495–506.
Naumann K H. 2003. COSIMA-a computer program simulating the dynamics of fractal aerosols[J]. Journal of Aerosol Science, 34(10): 1371–1397. DOI:10.1016/S0021-8502(03)00367-7
Mountain R D, Mulholland G W, Baum H. 1986. Simulation of aerosol agglomeration in the free molecular and continuum flow regimes[J]. Journal of Colloid & Interface Science, 114(1): 67–81.
Othman M, Latif M T, Mohamed A F. 2016. The PM10, compositions, sources and health risks assessment in mechanically ventilated office buildings in an urban environment[J]. Air Quality Atmosphere & Health, 9(6): 597–612.
Otto E, Fissan H, Park S H, et al. 1999. The log-normal size distribution theory of Brownian aerosol coagulation for the entire particle size range:part Ⅱ-analytical solution using Dahneke's coagulation kernel[J]. Journal of Aerosol Science, 30(1): 17–34. DOI:10.1016/S0021-8502(98)00038-X
Park S H, Lee K W. 2002. Analytical solution to change in size distribution of polydisperse particles in closed chamber due to diffusion and sedimentation[J]. Atmospheric Environment, 36(35): 5459–5467. DOI:10.1016/S1352-2310(02)00673-8
Polovnikov P V, Azarov I B, Veshchunov M S. 2016. Advancement of the kinetic approach to Brownian coagulation on the base of the Langevin theory[J]. Journal of Aerosol Science, 96: 14–23. DOI:10.1016/j.jaerosci.2016.02.006
孙在, 黄震, 王嘉松. 2007. 亚微米颗粒物的沉积与凝并的模拟与实验研究[J]. 上海交通大学学报, 2007, 41(10): 1710–1713. DOI:10.3321/j.issn:1006-2467.2007.10.032
Sun C, Yuan X, Yao X. 2016. Social acceptance towards the air pollution in China:Evidence from public's willingness to pay for smog mitigation[J]. Energy Policy, 92: 313–324. DOI:10.1016/j.enpol.2016.02.025
Veshchunov M S. 2015. Extension of the new kinetic approach to slow Brownian coagulation with finite sticking probability[J]. Journal of Engineering Thermophysics, 24(1): 1–11. DOI:10.1134/S1810232815010014
杨曼丽, 沈杰. 2016. 凝并过程对亚微米灰霾颗粒中痕量重金属分布的影响[J]. 环境工程学报, 2016, 10(9): 5037–5043. DOI:10.12030/j.cjee.201503264
Yu M Z, Lin J Z, Chan T L. 2008. A New Moment Method for Solving the Coagulation Equation for Particles in Brownian Motion[J]. Aerosol Science & Technology, 42(9): 705–713.
Yu M, Liu Y, Koivisto A J. 2017. An Efficient Algorithm Scheme for Implementing the TEMOM for Resolving Aerosol Dynamics[J]. Aerosol Science & Engineering: 1–19.