2. 中国气象局大气化学重点开放实验室, 北京 100081;
3. 上海点明信息技术有限公司, 上海 200940
2. Key Laboratory for Atmospheric Chemistry of CMA, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Shanghai Dianming Information Technology Limited Company, Shanghai 200940
近年来我国霾污染总体呈增加趋势, 并呈现持续时间长、范围广、影响大、污染重等特点(孙彧等, 2013;符传博等, 2014;丁一汇等, 2014), 准确的空气质量预报是开展环境气象预报业务服务的重要基础.因此数值模式预报成为定量研究大气污染问题的一种重要手段(唐孝炎等, 2006).目前国家级环境气象业务使用的雾-霾数值预报系统CUACE(CMA unified atmospheric chemistry environment)/Haze-fog由中国气象科学研究院研制, 提供08:00和20:00的84时效内逐3 h地面降水、相对湿度、地面水平能见度、PM2.5在内的6种大气污染物浓度、AQI(Air Quality Index)指数等环境气象预报指导产品(Gong et al., 2007;龚山陵等, 2008).
国内外被广泛应用的空气质量模式经历数十年的发展, 对多类污染物时空分布及其变化趋势具有较强的预报能力, 能够较好地模拟区域大气污染物浓度的时空分布规律(许建明等, 2005;Xu et al., 2008;Cheng et al., 2010;张美根等, 2005).但由于排放源清单的不确定性较大, 以及物理过程参数化和化学机制极为复杂, 数值模式对PM2.5、PM10、O3等重点污染物浓度的预报误差较大, 以CUACE为例:在兰州地区对SO2、CO和O3等级预报的准确率较高, 对PM2.5和NO2等级预报准确率不足50%(何金梅等, 2017);在乌鲁木齐, 当空气质量为良~中度污染时对PM2.5的预报准确率大于70%, 但对于重度污染、严重污染情况, 预报效果较差(李曼等, 2014);对合肥地区空气质量预报检验发现, AQI和PM2.5浓度的预报值接近实测值, PM10浓度预报值略小于实测值, O3浓度的预报值明显偏大(杨关盈等, 2017);在沈阳地区, CUACE模式对6种污染物(PM10、PM2.5、NO2、O3、SO2和CO)质量浓度的预报值普遍小于观测值, 对PM10浓度的预报存在严重低估, 且模式预报的空气污染等级与实际观测的空气污染等级相比存在较高的等级偏差率(李晓岚等, 2016).因此, 需对模式预报结果进行客观订正, 以改进污染物浓度预报, 提高环境气象业务预报水平.
近年来国内的空气质量数值预报模式订正技术也经历了长足发展:最初的模式订正技术主要利用实测数据对模式预报污染物浓度进行统计修正(Tie et al., 2003; 刘环珠等, 2004), 以应用较普遍的CMAQ模式为例, 诸多学者(许建明等, 2005;王庆梅等, 2008;张伟等, 2010;谢敏等, 2012;陈彬彬等, 2012;程兴宏等, 2013;尤佳红等, 2014)分别采用多元线性逐步回归、BP神经网、偏最小二乘回归、系统辨识实时迭代等多种统计方法对其输出结果进行订正, 该方法可显著降低由于污染源不确定性产生的模式系统误差(许建明等, 2005);国家气象中心也初步研究了基于“线性回归”和“kalman滤波”等方法的CUACE雾-霾预报模式的偏差订正技术;上述研究认为引入前期实测污染物浓度和预报浓度对预报结果进行修正是可行的.此后, 随着气象条件(如近地层风、气温、海平面气压、相对湿度)对大气污染物的传输、扩散、转化等作用的深入研究(李军等, 2009), 部分学者(许建明等, 2005;陈彬彬等, 2012;程兴宏等, 2013)开始尝试将多种气象要素实测值引入动力-统计订正模型, 该方案取得了一定的订正效果, 但订正时未考虑前期污染物实测浓度和气象条件的动态影响.2015年, 程兴宏等首次尝试将自适应偏最小二乘回归法和滚动订正技术相结合, 建立了一套非线性滚动订正模型, 将之应用于CMAQ模式预报PM2.5浓度订正技术中(程兴宏等, 2016).该模型不仅引入了实测PM2.5浓度以及附近的自动气象站风速、风向、温度、湿度、气压等地面气象实测数据, 也考虑了前10 d样本数的动态影响;经检验, 该模型对PM2.5浓度的订正效果较显著, 但不同季节、不同区域订正效果有所偏差.
为了更进一步的缩减不同季节、不同区域的订正偏差, 提升模型订正性能, 本文在程兴宏等的研究基础上, 首次将边界层特征物理量(如散度、涡度、垂直速度等)引入自变量方案中, 并针对不同季节、不同区域改进了最优自变量组合, 对未来3 d各站PM2.5浓度预报值进行滚动订正, 分析了订正前后PM2.5浓度的时空变化特征, 重点分析了该方法在秋冬季重污染过程的适用性及其改进效果, 本文的研究结果将对空气质量预报改进、雾霾天气的预报预警和大气污染的防治提供科学依据.
2 订正方法和使用资料(Correction method and datas) 2.1 订正方法目前中央气象台使用的环境气象模式以CUACE为主, 业务预报主要采用滑动平均法和卡曼滤波法模式订正主要针对6种污染物浓度进行订正应用, 进而求得空气质量指数和空气污染气象条件.但该方法订正效果有限(李军等, 2009).
本文采用自适应偏最小二乘回归法(Adaptive Partial Least Squares Regression, APLSR)进行动力-统计订正, 其是基于线性回归和最小二乘法的基础上建立的适用于高度非线性体系的统计方法, 其核心是计算隐变量、相似度、回归系数矩阵和因变量的预报值, 其计算公式分别为式(1)~(4).

|
(1) |

|
(2) |
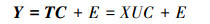
|
(3) |

|
(4) |
式中, T是n×k维隐变量矩阵, X是n×p维自变量矩阵, U是p×k维转换矩阵, SDi*为建模样本xi与预报样本x*之间的相似度, EDi*是两者之间的欧式距离, Y是n×q维因变量矩阵, C是k×q维回归系数矩阵, E是剩余误差矩阵,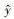
对样本数的选取, 参考前人的工作(程兴宏等, 2016)发现, 对于不同季节、不同地区采用前7 d和前10 d的数据建立的统计订正模型订正效果优于前3、5、15、20 d等方案.为了兼顾全国不同地区, 并且使各季节、各地区的订正模型较稳定, 本文使用了样本数更多的前10 d数据进行统计建模.
2.2 使用资料(1) 气象场实况资料:全国342个地级市气象站逐3 h 10 m风速、10 m风向、2 m温度、2 m湿度、海平面气压实测数据.
(2) 污染物实测资料:中国环境监测总站(http://106.37.208.233:20035/)公布的1493个国控点逐时PM10、PM2.5、SO2、NO2、O3、CO的浓度值, 选取与342个气象站最近的环境监测站点.
(3) 气象要素预报场:0.125°×0.125°EC细网格每天08:00、20:00起报的未来240 h逐3 h 10 m风速、10 m风向、2 m温度、2 m湿度、海平面气压值、850 hPa露点温度、850 hPa垂直速度、850 hPa涡度、850 hPa散度, 并采用双线性方法插值到342个气象站;
(4) 污染物浓度预报场:54 km和15 km分辨率的GRAPES-CUACE(下文中分别简写为CUACE-54 km、CUACE-15 km)模式预报的每天08、20时起报的逐3 h上述6种污染物浓度, 同样并采用双线性方法插值到342个气象站.
3 全国不同地区订正方案优选(Choosing the optimal independent variable combination schemes for different regions of China)自变量选取时除考虑前期污染物实测浓度对预报浓度的影响外, 亦考虑了前期气象条件的动态影响.为了细化参数方案, 将全国342个城市按照各自省份划分为31组, 每组以直辖市、省会城市为代表站进行建模.分别针对2015年1、4、7、10月31个省会城市进行自变量优选, 并采用其他月份数据进行效果评估, 改进模型参数, 最终选取不同区域不同季节的最优自变量组合方案.
3.1 自变量初选前期研究(程兴宏等, 2016)发现多数情况下不同地区、不同季节PM2.5实测浓度与10 m风速、风向、2 m温度、2 m湿度、地面气压的相关性均较好, 而且通过了99.9%置信度水平检验.为了分析高空气象要素对污染物浓度订正效果的影响, 本文以PM2.5为例, 分别计算了春、夏、秋、冬4个季节31个省会城市PM2.5观测浓度与露点温度、850 hpa散度、垂直速度、涡度等4种高空气象自变量之间的相关系数, 并进行95%置信度水平检验.检验结果表明, 31个城市PM2.5浓度与4个变量的相关系数均通过了显著性检验(表略), 但不同地区不同季节其相关性有所差异, 在后续的研究中将优选上述5种地面气象要素与4种高空气象要素的最优组合方案, 以改进不同季节不同地区的订正效果.
3.2 优选敏感试验方案为选取31个省会城市4个季节的最优自变量组合方案, 分别设计了15组订正试验方案, 如表 1所示, 其中ws、wd、t、rh、p、td、omega、vor、div分别表示水平风速、风向、气温、相对湿度、气压及850 hpa露点温度、垂直速度、涡度、散度.各城市根据不同季节td、omega、vor、div这4个变量的相关显著性检验结果, 将过检变量分别与ws、wd、t、rh、p这5个基本变量进行组合, 共计15种组合方案;然后采用15种组合变量分别进行订正试验, 最终根据相关系数和均方根误差两个指标(其中均方根误差权重较大)进行判断, 选出各个站点不同季节的最优组合方案.
| 表 1 31个城市不同季节最优自变量组合方案试验 Table 1 The test of the optimal combination scheme of independent variables in different seasons of 31 cities |
表 2给出了7个重点区域的典型城市不同季节自变量组合最优方案列表及其订正效果;表 3为31个省会城市、直辖市采用自变量最优组合方案订正后均方根误差减小比例.总体而言, 除54517、56294两个城市因PM2.5浓度观测和预报资料缺测外, 其他城市不同季节均进行了订正试验, 得出了各个城市不同季节的最优自变量组合方案, 订正有效率为99.16%, 全国31个省会城市、直辖市4个季节采用最优方案订正后均方根误差比CUACE模式预报平均减小26.4%.
| 表 2 7个重点城市不同季节自变量组合最优方案列表及其订正效果 Table 2 The optimal combination scheme of independent variables and the correction effect in different seasons of 7 cities |
| 表 3 31个省会城市采用自变量最优组合方案订正后PM2.5浓度均方根误差减小比例 Table 3 The decreasing rate of RMS error of 31 cities with the optimal combination scheme of independent variables |
为减小计算量, 采用区域内多数站点的最优方案作为各区域的最优组合方案进行2016年秋冬季的历史订正回算, 表 4为5个重点区域以及其他地区的最优方案.
| 表 4 全国5个重点区域以及其他地区的最佳自变量组合方案优选列表 Table 4 The optimal combination scheme of independent variables of 5 key regions and other places |
采用全国5个重点区域及其他地区的最佳自变量组合方案回算了基于CUACE模式预报结果的2016年1—3月(冬春季)全国342个城市6种污染物的订正值, 并与同期CUACE模式54 km、15 km预报结果及气象中心业务运行的线性订正结果进行比较, 重点检验了不同模式分辨率、不同订正方法的PM2.5浓度订正改进效果.
图 1给出了2016年1—3月342个城市CUACE模式54 km、15 km预报逐3 h PM2.5浓度及线性回归订正、APLSR非线性滚动订正值与实测值的散点分布特征.对比图 1a和1b可知, GRAPES-CUACE模式(无论是54 km分辨率还是改进的15 km分辨率)逐3 h PM2.5浓度预报与实测值的散点多分布于对角线下方, 即多数时刻、多数站点预报值低于实测值, 而且分布较分散, 相关系数较小;经过线性订正后(图 1c), PM2.5浓度与实测值的散点分布有所改进, 但无论是相关系数还是订正偏差改进幅度较有限;经过APLSR非线性订正后, PM2.5浓度与实测值的分布得到显著改进, 即散点明显集中在对角线附近, CUACE模式预报偏小或偏大的程度得到明显改善, 与CUACE模式直接预报相比, 相关系数提高了0.43以上, 即APLSR非线性订正浓度更接近实测值.
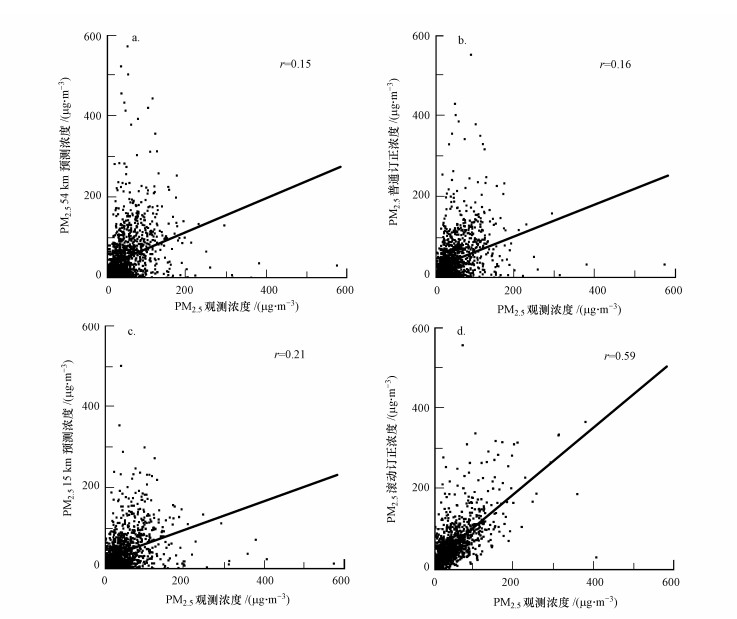 |
| 图 1 2016年1—3月342个城市CUACE模式54 km (a)、15 km (b)预报逐3 h PM2.5浓度及线性回归订正(c)、APLSR非线性滚动订正值(d)与实测值的散点分布图 Fig. 1 Scatter plots of hourly forecasted PM2.5 concentrations by CUACCE-54 km(a), CUACCE-15 km(b), linear correction(c), APLSR correction(d) and observations during January-March 2016, at 342 city stations in China |
图 2为2016年冬春季(1—3月)全国342个城市气象站逐3 h PM2.5浓度预报和订正偏差的概率分布特征.可看出, 无论是模式直接预报的PM2.5浓度与实测浓度的偏差(图 2a、2b), 还是经过两种方法订正后的浓度偏差(图 2c、2d)均表现为正态分布特征, 但两种模式和线性订正的PM2.5浓度预报偏差大部分介于±100 μg·m-3之间, 而且最大概率分布范围亦较宽.经过APLSR非线性订正后, 大部分误差集中分布于±50 μg·m-3之间, 最大概率分布范围较窄, 介于±10 μg·m-3之间, 明显改善了两种模式PM2.5预报浓度较实况偏低的状况.
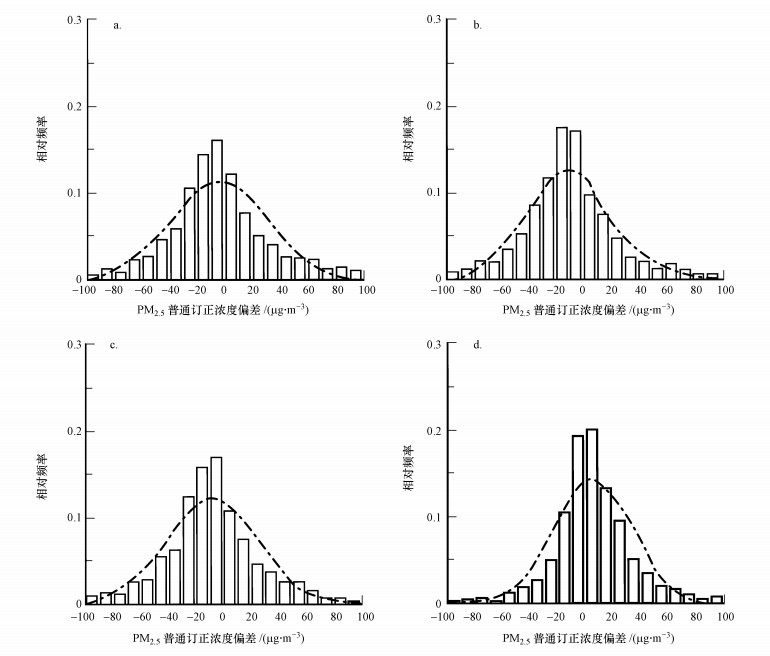 |
| 图 2 2016年1—3月342个城市CUACE模式54 km、15 km预报逐3 h PM2.5浓度及线性回归订正、APLSR非线性滚动订正值与实测值偏差的概率分布图 Fig. 2 Probability distribution of deviations between observations and hourly forecasted PM2.5 concentrations by CUACE-54 km(a), CUACE-15 km(b), linear correction(c), APLSR correction(d) during January—March 2016 at 342 city stations in China |
上述分析结果表明, 冬春季CUACE模式预报的PM2.5浓度偏差较大, 误差分布范围较宽;普通线性订正改进不明显;经过APLSR非线性订正后, 误差明显减小, 而且多数时刻PM2.5浓度偏差集中分布于±10 μg·m-3, 订正效果较显著.
4.3 误差统计表 5给出了2016年1—3月全国和重点区域CUACE-54 km、CUACE-15 km分辨率模式预报的逐时PM2.5浓度、线性回归订正、APLSR非线性滚动订正值与实测值的相关系数及其多项误差统计.由表 5可看出, 无论是CUACE-54 km还是CUACE-15 km分辨率模式预报的2016年1—3月全国及京津冀、长三角、珠三角、川渝4个重点污染区域PM2.5逐3 h预报浓度与实测值的相关系数较小, 预报平均偏差、绝对平均偏差和均方根误差的绝对值均较大.但总体而言, CUACE-15 km分辨率模式预报的PM2.5浓度预报效果较CUACE-54 km有所改善, 其中长三角地区PM2.5浓度预报效果较好, 准确率达到了69.3, 珠三角地区和京津冀地区次之, 川渝地区预报效果较差.线性回归订正后的PM2.5浓度预报效果改进一般, 部分地区甚至不如模式直接输出的PM2.5浓度预报效果.经APLSR非线性滚动订正后, PM2.5浓度订正值与实测值的相关系数显著增加, 各项订正误差显著减小, 准确率大幅上升, 全国和京津冀、长三角、珠三角、川渝等4个重点区域的准确率相对于CUACE-15 km分辨率模式预报的准确率分别上升了15.5、8.1、3.5、4.8、9.7, 相对于线性回归订正后的准确率分别上升了18.3、17.4、2.8、5.5、12.0.全国和京津冀地区PM2.5订正浓度与实测浓度的相关系数分别提高至0.59、0.81;全国和上述4个重点区域的绝对平均偏差相对于CUACE-15 km分辨率模式预报的绝对平均偏差分别减小了8.5、9.7、13、2.6、1.7 μg·m-3, 相对于线性回归订正后的绝对平均偏差分别减小了12.2、94.1、1.4、5.3、6.2 μg·m-3.
| 表 5 2016年1—3月重点地区CUACE模式54 km、15 km预报误差以及线性回归订正、APLSR非线性滚动订正PM2.5浓度误差统计表 Table 5 Relative coefficients and bias between hourly forecasted, corrected PM2.5 concentrations and observations during January—March 2016 at key regions in China |
就PM2.5浓度订正准确率而言, 4个重点区域中长三角地区PM2.5浓度订正效果最好, 准确率最高, 可达72.3;珠三角地区次之, 准确率可达66.3;京津冀和川渝地区订正效果稍差, 但是准确率也高达63.6和62.6.
针对不同地区, 该方法订正效果存在地域差异, 主要原因如下:①由于计算量较大, 本文将全国分为京津冀、长三角、珠三角等5个重点区域和其他区域, 同一个研究区域内分别用一套最佳自变量组合方案来订正该区域内所有站点, 因此并非每个站点都可取得最佳的订正效果;②本文使用的EC细网格气象预报结果本身存在一定误差, 尤其对于复杂地形(如川渝地区)边界层内各气象要素预报误差较大;③为了计算方便, 目前针对全国所有站点统一采用前10 d的数据作为训练样本, 但不同城市的最佳样本数亦有所不同.本文将在今后的研究中针对不同站点采用不同的最尤自变量组合方案和最佳样本数, 并采用气象资料同化方法减小气象预报误差, 以改进各城市的订正效果.
本文亦根据中国环境保护部(2012)发布的PM2.5浓度日均值二级标准和实测浓度资料, 将2016年1月1日—3月31日分为污染日和非污染日, 分别计算全国342个气象站PM2.5浓度预报、订正日均值的准确率以及相关系数、平均偏差、绝对平均偏差、均方根误差等评估指标(表 6).
| 表 6 2016年1—3月污染日与非污染日CUACE模式54 km、15 km预报误差以及线性回归订正、APLSR非线性滚动订正PM2.5浓度误差统计表 Table 6 Accurate forecasting rate, relative coefficients and bias between hourly forecasted, corrected PM2.5 concentrations and observations in polluted and clean days during January—March 2016 at 342 city stations in China |
可看出, 不论是CUACE-54 km、CUACE-15 km分辨率模式直接预报还是线性订正结果, PM2.5浓度预报的准确率较小, 污染日在45%左右, 非污染日准确率稍高, 能达到50%左右;预报值与实测值的相关系数较小, 污染日的相关系数甚至为负值, 非污染日相关系数分别为0.33和0.46;平均偏差、绝对平均偏差、均方根误差均较大.经过APLSR非线性滚动订正后, 其准确率和相关系数均有较大提高, 平均偏差、绝对平均偏差、均方根误差均大幅减小;具体来看, 针对CUACE-15 km分辨率模式, 污染日和非污染日的准确率分别提升了57.5%和25.9%, 相关系数分别提升了304.8%和15.2%, 绝对平均偏差分别减小了38.9%和18.7%, 均方根误差分别减小了21.8%和8.5%.
总体而言, 非污染日PM2.5浓度预报效果总体优于污染日, 且CUACE-15 km分辨率模式预报效果优于CUACE-54 km分辨率模式预报;APLSR非线性滚动订正效果明显优于两种模式直接预报和线性订正方法, 对污染日和非污染日订正后的预报准确率均有较大提高, 对污染日的改进效果要优于非污染日.
4.4 重污染个例订正效果分析为了验证改进后的订正方案对重污染过程的订正效果, 针对京津冀、长三角、珠三角、川渝地区等4个重点区域分别以北京、上海、广州、乐山为代表城市, 分别选取2018年3月7日—14日、2018年3月7日—15日、2018年1月15日—22日、2017年12月22日—29日等4次以PM2.5为首要污染物的重污染过程, 分析其订正前后的预报浓度与实测浓度的关系, 如图 3所示, 其中, CUACE模式预报结果均选取最近时刻起报的24 h内逐3 h预报值.
 |
| 图 3 重污染过程期间PM2.5浓度实测、预报及订正的时间变化图(a.北京(2018.03.07—2018.03.14), b.上海(2018.03.07—2018.03.15), c.广州(2018.01.15—2018.01.22), d.乐山(2017.12.22—2017.12.29) Fig. 3 Temporal variation of forecasted, corrected and observed PM2.5 concentrations at (a.Beijing(7th to 14th March 2018), b.Shanghai(7th to 15th March 2018), c.Guangzhou(15th to 22th January 2018), d.Leshan(22th to 29th December 2017) in heavy pollution period |
以PM2.5浓度预报订正为例, 订正前, 北京、上海、广州、乐山的模式预报结果与实况观测浓度的绝对平均误差分别为52.34、33.28、44.87、46.07 μg·m-3;订正后, 上述4个城市的绝对平均误差分别减小到46.02、17.76、28.42、37.91 μg·m-3, 减小比例达12.07%、46.63%、36.66%、17.71%.订正前, 北京、上海、广州、乐山的模式预报结果与实况观测浓度的相关系数分别为0.58、0.36、0.65、0.24;订正后, 上述4个城市的相关系数分别上升到0.73、0.44、0.76、0.63, 提升了25.86%、22.22%、16.92%、162.5%.上述4个城市典型重污染过程订正后的绝对平均偏差均有所下降, 相关系数均有明显上升, 说明该订正方法适用于不同地区的不同重污染过程的预报.
5 结论(Conclusions)1) 无论是CUACE-54 km模式还是CUACE-15 km模式, 冬春季全国342个城市预报PM2.5浓度普遍较实况观测浓度要小, 且模式预报PM2.5浓度与实况观测浓度的相关系数较低;但总体而言, CUACE-15 km分辨率模式预报的PM2.5浓度预报效果较CUACE-54 km有所改进, 其中长三角地区PM2.5浓度预报效果较好, 准确率达到了69.3, 珠三角地区和京津冀地区次之, 川渝地区预报效果较差.
2) 经过大量敏感性试验, 优选了全国31个省会城市、直辖市以及5个重点地区的最优自变量组合方案, 从各区最优方案来看, 除珠三角和川渝地区考虑高空气象要素的订正效果更优外, 其他地区可直接采用5种地面常规气象要素.
3) 经APLSR非线性订正后的PM2.5浓度订正值与实测值的散点分布特征明显优于两种不同分辨率的模式预报浓度, 即订正值较接近于实测值, 相关系数明显提高.从偏差概率分布来看, 两种不同分辨率的模式预报PM2.5浓度预报偏差较大, 误差分布范围较宽;APLSR订正后误差明显减小, 而且多数时刻PM2.5浓度偏差集中分布于±10 μg·m-3附近, 订正效果较显著.
4) 从京津冀、长三角、珠三角、川渝地区等重点区域的订正效果来看, 经过APLSR非线性订正后, PM2.5浓度订正值与实测值的相关系数显著增加, 各项订正误差显著减小, 准确率大幅提高.长三角地区PM2.5浓度订正效果最好, 珠三角地区次之, 京津冀和川渝地区订正效果稍差.
5) 本文的APLSR动力-统计滚动订正方法亦适用于非污染日和污染日全国范围的PM2.5预报浓度订正, 两种天气过程PM2.5浓度的订正效果均较显著, 即污染日和非污染日的准确率分别提升了57.5%和25.9%, 相关系数分别提升了304.8%和15.2%, 绝对平均偏差分别减小了38.9%和18.7%, 均方根误差分别减小了21.8%和8.5%.
6) 针对北京、上海、广州、乐山的不同重污染过程, 订正后的平均绝对误差分别减小了12.07%、46.63%、36.66%、17.71%, 相关系数分别提升了25.86%、22.22%、16.92%、162.5%, 说明该订正方法适用于不同地区的不同重污染过程的预报.
基于“自适应偏最小二乘回归法”建立的CUACE雾-霾预报偏差非线性滚动订正改进方法能够显著改进PM2.5浓度的预报效果, 主要因为引入了PM2.5的实测浓度和气象条件, 并考虑了不同季节不同地区的气象条件影响差异, 对GRAPES-GUACE模式预报的PM2.5浓度进行实时动态修正.但不同地区的订正效果仍存在地域性差异, 将在今后的研究中针对不同站点采用不同的最尤自变量组合方案和最佳样本数, 并采用气象资料同化方法减小气象预报误差, 以改进各城市的订正效果.另外由于O3亦逐渐成为京津冀、长三角、珠三角、川渝地区等重点区域的主要污染物, 本文今后将采用APLSR方法对O3浓度预报进行订正方法研究.
陈彬彬, 林长城, 杨凯, 等. 2012. 基于CMAQ模式产品的福州市空气质量预报系统[J]. 中国环境科学, 2012, 32(10): 1744–1752.
DOI:10.3969/j.issn.1000-6923.2012.10.003 |
Cheng X H, Xu X D, Ding G A. 2010. An emission source inversion model based on satellite data and its application in air quality forecasts[J]. Science China Earth Sciences, 53(5): 752–762.
DOI:10.1007/s11430-010-0044-9
|
程兴宏, 李德平, 徐祥德, 等. 2013. 北京地区CMAQ源同化模式预报PM10产品订正方法研究[C]//中国环境科学学会2013年学术年会
|
程兴宏, 刁志刚, 胡江凯, 等. 2016. 基于CMAQ模式和自适应偏最小二乘回归法的中国地区PM2.5浓度动力-统计预报方法研究[J]. 环境科学学报, 2016, 36(8): 2771–2782.
|
丁一汇, 柳艳菊. 2014. 近50年我国雾和霾的长期变化特征及其与大气湿度的关系[J]. 中国科学:地球科学, 2014, 44(1): 37–48.
|
符传博, 丹利. 2014. 重污染下我国中东部地区19602010年霾日数的时空变化特征[J]. 气候与环境研究, 2014, 19(2): 219–226.
DOI:10.3878/j.issn.1006-9585.2014.13213 |
Gong S L, Zhang X Y. 2008. CUACE/Dust-an integrated system of observation and modeling systems for operational dust forecasting in Asia[J]. Atmospheric Chemistry and Physics, 8(9): 2333–2340.
DOI:10.5194/acp-8-2333-2008
|
龚山陵, 张小曳. 2008. CUACE/Dust:亚洲沙尘暴计算机业务预报系统[J]. 计算机与应用化学, 2008, 25(9): 1061–1067.
|
何金梅, 刘抗, 王玉红, 等. 2017. CUACE模式在兰州城市空气质量预报中的检验订正[J]. 干旱气象, 2017, 35(3): 495–501.
|
李曼, 张载勇, 李淑娟, 等. 2014. CUACE系统在乌鲁木齐空气质量预报中的效果检验[J]. 沙漠与绿洲气象, 2014, 8(5): 63–68.
|
李晓岚, 马雁军, 王扬锋, 等. 2016. 基于CUACE系统沈阳地区春季空气质量预报的校验及修正[J]. 气象与环境学报, 2016, 32(6): 10–18.
|
李军, 孙春宝, 刘咸德, 等. 2009. 气象因素对北京市大气颗粒物浓度影响的非参数分析[J]. 环境科学研究, 2009, 22(6): 663–669.
|
刘还珠, 赵声蓉, 陆志善, 等. 2004. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 2004, 15(2): 181–191.
|
刘慧, 饶晓琴, 张恒德, 等. 2017. 环境气象业务数值模式预报效果对比检验[J]. 气象与环境学报, 2017, 33(5): 17–24.
|
孙彧, 马振峰, 牛涛, 等. 2013. 最近40年中国雾日数和霾日数的气候变化特征[J]. 气候与环境研究, 2013, 18(3): 397–406.
DOI:10.3878/j.issn.1006-9585.2013.12170 |
唐孝炎, 张远航, 邵敏. 2006. 大气环境化学(第二版)[M]. 北京: 高等教育出版社: 447–449.
|
Tie X, Emmons L, Horowitz L, et al. 2003. Effect of sulfate aerosol on tropospheric NOx and ozone budgets:Model simulations and TOPSE evidence[J]. Journal of Geophysical Research:Atmospheres, 108(D4): 8364.
DOI:10.1029/2001JD001508
|
王庆梅, 张雪梅, 韩光. 2008. 兰州市大气污染特征与污染预报技术研究[J]. 中国环境监测, 2008(3): 56–62.
|
谢敏, 钟流举, 陈焕盛, 等. 2012. CMAQ模式及其修正预报在珠三角区域的应用检验[J]. 环境科学与技术, 2012, 35(2): 102–107.
|
许建明, 徐祥德, 刘煜, 等. 2005. CMAQ-MOS区域空气质量统计修正模型预报途径研究[J]. 中国科学D辑:地球科学, 2005, 35(增刊Ⅰ): 131–144.
|
Xu X D, Xie L A, Cheng X H, et al. 2008. Application of an Adaptive Nudging Scheme in Air Quality Forecasting in China[J]. J Appl Meteorol Climatol, 47: 2105–2114.
DOI:10.1175/2008JAMC1737.1
|
杨关盈, 邓学良, 吴必文, 等. 2017. 基于CUACE模式的合肥地区空气质量预报效果检验[J]. 气象与环境学报, 2017, 33(1): 51–57.
|
尤佳红. 2014. 上海地区霾集合预报研究[D]. 上海: 华东师范大学
http://cdmd.cnki.com.cn/Article/CDMD-10269-1014322252.htm |
张美根. 2005. 多尺度空气质量模式系统及其验证Ⅰ.模式系统介绍与气象要素模拟[J]. 大气科学, 2005, 29(5): 805–813.
|
张伟, 王自发, 安俊岭, 等. 2010. 利用BP神经网络提高奥运会空气质量实时预报系统预报效果[J]. 气候与环境研究, 2010, 15(5): 595–601.
|
中国环境保护部. 2012. GB 3095-2012. 环境空气质量标准[S]. 北京: 中国环境科学出版社
|
 2018, Vol. 38
2018, Vol. 38


