2. 天津大学表层地球系统科学研究院, 天津 300072
2. Institute of Surface-Earth System Science, Tianjin University, Tianjin 300072
对流层中臭氧是由氮氧化物(NOx)、一氧化碳(CO)等污染物经过光化学反应产生的二次污染物, 不但可经过化学反应产生羟基(OH)自由基影响温室效应, 而且危害动植物生长和健康(杨昕等, 1999;蒋璐璐等, 2016;刘烽等, 2017).作为大气六大污染物之一, 近地面臭氧污染的监测是空气质量预报和防治的重要内容之一.
目前臭氧、PM2.5等空气污染物预报方法主要分为数值模式预报和统计模型预报两类(郭晓雷, 2011).数值模式预报方法以动力学理论为基础, 利用偏微分方程来模拟空气污染物在大气中扩散的物理化学等一系列复杂的过程(常明等, 2016;周广强等, 2015;沈劲等, 2011), 在描述物理过程方面具有较完善的理论基础, 但预报结果的优劣很大程度上依赖于模型输入的排放清单精度.由于建立高精度、高分辨率排放源清单难度大、模式运行复杂且计算量大, 一定程度上限制了数值预报方法的广泛应用.统计预报模型以污染物浓度及气象要素观测数据为基础, 通过多元线性回归法、神经网络法、决策树法等数学统计方法构建大气污染物和气象因子之间的数值关系模型, 利用气象因子作为模型输入预测大气污染物浓度.统计预报模型具有构建简单、使用方便、且不需要污染源排放清单作为模型输入数据等优点, 因此, 在区域空气质量预报中得到广泛应用(Durão et al., 2016;刘闽等, 2014;宋榕荣等, 2012;安俊琳等, 2010;Jing-Hui et al., 2012;Debry and Mallet, 2014).如Durão等(2016)首先利用决策树确定臭氧的预报因子, 然后采用多层感知模型预报监测站点处的臭氧浓度.刘闽等(2014)采用逐步回归分析法建立了沈阳市冬季环境空气质量统计预报模型, 对PM2.5、PM10、SO2、NO2、CO及O3的浓度进行了预测.孙峰等(2004)对比研究了线性回归模型、CART决策树模型、CART与线性回归结合模型、动态统计预报模型以及多点预报模型各自优缺点;黄思等(2015)采用线性回归集成方法对多个模式的预报结果进行优化, 使预报精度得到了提升.以上研究表明, 通过构建空气污染物与气象要素之间统计模型预报空气污染物是行之有效且得到广泛应用的方法.
本文以徐州市为例, 利用分类回归树(CART)、随机森林(RF)、M5模型树方法, 建立徐州市臭氧浓度决策树模型并预报近地面臭氧浓度分布状况;其次, 以WRF模式输出的区域气象场作为臭氧决策树模型的输入数据, 预测区域网格化臭氧浓度动态分布;最后采用多模式集合预报方法, 基于周步长决策树模型预报值及观测值之间的回归关系, 进一步优化模型.
2 研究数据及研究方法(Research data and methods) 2.1 研究区概况徐州市位于我国华东地区, 地理范围介于东经116.00°~ 119.32°, 北纬32.85°~ 35.56°(图 1), 属暖温带半湿润季风气候, 雨量适中, 雨热同期, 年平均气温14 ℃, 年日照时数为2284~2495 h, 日照率52%~57%, 年均降水量800~930 mm.徐州市是华东地区重要的工业城市, 工业主要以煤炭、电力、建材等重工业为主, 是江苏省空气污染最为严重的地区之一.
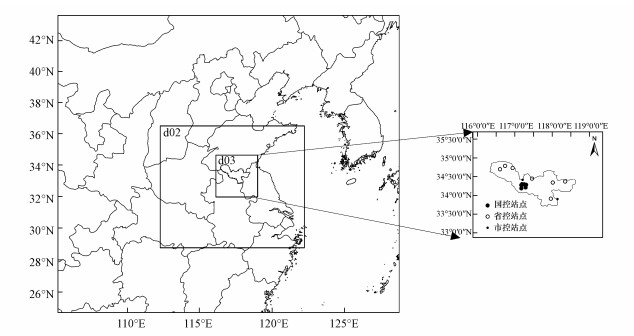 |
| 图 1 研究区及WRF模式嵌套区设置 Fig. 1 Study area and nested domain for the WRF model |
臭氧站点监测数据来源于徐州市自动监测监控综合应用系统.该系统包含徐州市7个国控、6个省控和5个市控空气质量自动监测站(图 1), 实时获取小时步长SO2、NO2、PM10、CO、O3和PM2.5大气污染物浓度数据.本研究以国控站2015年1月1日—12月31日逐小时的臭氧浓度及气象观测数据(风速、风向、温度、湿度、气压、降水量)作为决策树模型训练样本数据集, 利用2016年1月、4月、7月和10月逐小时监测数据对模型进行验证.站点观测数据用于模型建立和验证前首先进行质量控制, 质量控制中剔除明显异常值同时尽可能保证可用数据量.
气象数据中风向数据是以风向与正北方向的夹角的角度值为记录形式.为了更好的将风这一重要要素引入模型中, 数据处理时以向量的形式综合风速和风向两要素, 并利用坐标的形式表示风矢量, 其中风向量的模表示风速的大小, x值等于风速乘以风向角的正弦值, y值等于风速乘以风向角的余弦值.
在区域臭氧浓度空间分布预测中, 以WRF模式模拟的区域气象场作为决策树预测模型气象驱动数据.WRF模式是目前在全球得到广泛应用的中尺度预报模式和同化系统(Michalakes et al., 2004).重点考虑从云尺度到天气尺度等重要天气的预报, 水平分辨率重点考虑1~10 km空间尺度. WRF模式系统在预报各种天气中都具有较好的性能(章国材, 2004).本研究中WRF模式采用Lambert地图投影方式和3层区域嵌套网格设置(图 1), 垂直层共23层, 模式层顶气压为50 hPa.决策树模型采用徐州地区WRF第三层嵌套区域输出气象场数据, 水平分辨率为3 km, 中心经度为117°E, 中心纬度为35°N.
2.3 决策树算法利用CART、RF和M5模型树3种决策树算法建立臭氧统计分析预报模型.CART决策树算法通过计算每个特征的Gini系数, 选择分裂属性, Gini系数的计算如下:
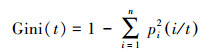
|
(1) |
式中, 假设整个样本集为S, 类别集为{N1, N2, …, Nk}, 总共分为k类, 每个类对应一个样本子集Si(1≤i≤k). pi(i/t)表示目标类别i在节点t中出现的概率.设|S|为样本集S的样本数, |Ni|为样本集S中属于类Ni的样本数, pi=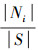
RF算法是以决策树为基础分类器, 利用投票的机制得出预测结果.依据bootstrap抽样技术有放回地随机从数据集中抽取部分数据作为每个决策树的训练样本, 以剩余数据作为各决策树的验证样本, 进行预测时, 首先输出每个决策树预测值, 然后利用简单投票法将所有预测结果进行综合从而得到最后的预测结果(Breiman, 2001).
M5模型树是在CART基础上的进一步发展, 二者主要的区别在于叶节点的构成和划分样本空间的标准.M5模型树的叶节点是一个根据该处样本建立的回归方程.其样本空间分割标准是降低样本标准差而非平方误差, 即将目标属性的标准差视为误差的度量, 计算样本属性差异化SDR(standard deviation reduction)的公式如下:
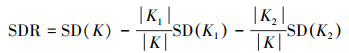
|
(2) |
式中, K代表总样本空间, |K|为总样本空间的样本数, K1和K2分别是总样本空间中的两个子样本空间, 其并集是总样本空间.利用SD为样本属性标准差, 取SDR最大者作为分割点(Quinlan, 1992).
由于构建决策树的属性点分割规则和树结构的不同, 3种决策树算法之间具有较大差异.CART算法以所有到达叶节点的样本均值作为模型的预测输出, 其优点是算法简单, 便于理解, 但由于CART算法是根据所有参与训练的样本建立一棵树, 其泛化能力较弱.RF利用bagging策略将训练样本随机分组, 并建立多个以CART算法为基础的决策树, 每棵树均参与预测, 最终通过专家投票机制得到预测结果, 克服了CART泛化能力弱的问题.M5模型树的叶节点为一个回归方程, 该方程由到达叶节点的样本建立, 所以预测精度更高.且M5模型树处理高维数据更加容易, 克服了CART算法的计算量会随着数据量的增加而迅速增大的缺点.
2.4 多模式集合预报不同模型对于污染物的模拟有不同的优势, 采用简单平均、权重线性集成、线性回归集成和人工神经网络等方法集合多模型预报结果通常可得到优于单个模型预报值(黄思等, 2015;王茜等, 2010).本研究中采用线性回归集成法对CART决策树和RF预测结果进行集合.基本原理如下:
假设有N个预报模型, 以容量为k的独立样本对某种预报对象作出预测, 其结果分别为Y1(t), Y2(t), …, Yn(t), 其中t=1, 2, …, k.以预报结果作为自变量, 依据最小二乘法原理, 可得到线性回归集成的预报方程为:
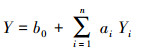
|
(3) |
式中, Yi为第i个模型的预报结果, 参数b0为预报对象的平均值, ai是第i种预报方法的权重系数.
2.5 误差评估研究中误差评估指标包括相关系数(r)、平均绝对误差(MAE)、均方根误差(RMSE)及准确率作为预报结果误差评估指标, 其具体计算公式如式(4)~(6)所示.
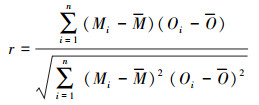
|
(4) |
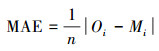
|
(5) |
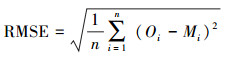
|
(6) |
式中, n代表着样本的个数, Mi表示模型模拟值或预报值, Oi代表污染物观测浓度值.相关系数能够反映模型模拟值或预报值总体变化趋势与观测值的相似程度.平均绝对误差和均方根误差反映了模拟值或预报值与观测值之间的偏离程度.综合考虑这两个评估指标, 能够较好地反映出预报的准确性.
准确率是指根据空气质量分指数(IAQI: Individual Air Quality Index)及对应污染物项目浓度限值, 将污染物浓度分为7级(表 1), 根据污染物浓度限值分别计算预报值及观测值等级, 并计算污染物浓度预报值的准确率(式(7)).
| 表 1 臭氧IAQI浓度限值 Table 1 Limit values of ozone IAQI |
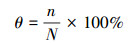
|
(7) |
式中, n表示与观测值计算所得的IAQI落在同一限差区间的预报值的个数, N为所有预报值的个数.
3 结果与分析(Results and analysis) 3.1 统计预报模型建立与验证本文利用R语言进行臭氧决策树统计预报模型建模与预测.由于从徐州市自动监测监控综合平台仅获取国控站点处气象要素观测数据, 所以, 首先以徐州市7个国控站点2015年1月1日—12月31日逐小时臭氧浓度和气象要素数据作为训练样本, 分别建立具有空间意义的臭氧CART、RF和M5模型树预报模型.其次, 分别以2016年1月、4月、7月、10月所有国控站点逐小时气象要素观测数据作为建立的3种统计预报模型输入, 得到臭氧浓度模拟值, 并将臭氧模拟值与该时间段内臭氧浓度观测值进行对比分析.
图 2所示为臭氧模拟值精度验证泰勒图, 每个点表示一个监测站点处模拟值与观测值的误差统计量.其中模拟值到原点的距离代表其相对于观测值(坐标轴1值点)的归一化标准差, 散点越接近弧线1表明模拟值与预测值的偏差越小, 模拟值方位角的余弦表示其与观测值的相关系数, 预测值到观测值的距离为归一化均方根误差.散点分布比较集中, 表明模型在7个站点处的模拟精度较一致, 且散点多数位于相关系数0.6~0.8区间, 其中4月模拟值与观测值的相关系数最高, 一半散点位于相关系数0.8~0.9区间.此外, 4个月中多数站点的归一化标准偏差小于1, 说明模拟值普遍低估.RF模型在1月、4月和10月的多数散点相关系数大于其他两种模型, M5模型树7月的模拟值相关系数较高;而3种模型模拟值偏差的差异较小.以上分析结果表明臭氧模型在所有国控站点处均有较好的模拟效果.
 |
| 图 2 臭氧模型精度验证泰勒图(图a~d分别表示1、4、7、10月模型精度验证图) Fig. 2 Taylor figure of ozone model verification |
表 2给出了3种决策树统计模型分别在1、4、7、10月4个月臭氧浓度模拟结果的误差统计.臭氧浓度模拟值与观测值相关系数的均值为0.68, 表明3种决策树模型均可较好模拟不同季度臭氧浓度的变化趋势.其中模型对4月臭氧浓度变化的模拟效果最好, 但平均绝对误差和均方根偏大;1月臭氧浓度模拟值与观测值相关系数最低, 但绝对平均误差和均方根误差较小.对比3种模型的模拟效果, 1月、4月和10月RF模拟值与观测值的相关系数最大, 表明RF模拟值的变化趋势在多数时段与观测值变化特征的一致性较好.RF与CART模型1月和10月的模拟值偏差最小, M5模型树4月和7月臭氧浓度模拟值的平均绝对误差和均方根误差最小, 即M5模型树在该时段模拟值偏差较小.
| 表 2 臭氧模拟值与观测值对比 Table 2 Comparison of ozone simulation and observation |
图 3显示各月15—21日国控站黄河新村站处臭氧浓度及CART(a)、RF模型(b)和M5模型树(c)模拟值与观测值时间序列图.1月臭氧浓度最低, 4月和7月臭氧浓度普遍高于其他两个月.臭氧浓度在一天中变化曲线呈单峰分布, 极小值与极大值分别出现在8:00和15:00左右.4月和7月的决策树模型臭氧浓度模拟值曲线与观测值曲线贴合程度最好, 但通常在臭氧浓度极大值时刻模拟值小于观测值;模型在1月和10月臭氧浓度较低时段模拟值偏高.3种模型对于臭氧浓度极大值的模拟效果在不同时期有所差别, M5模型树在4月和10月臭氧浓度极大值时刻模拟值偏差较小, RF在1月和7月极大值时刻模拟效果较好;3种决策树模型模拟值曲线在极小值时刻贴近观测值, 其中4月和7月臭氧浓度低水平时刻模拟值与观测值曲线基本重合.RF模型的模拟值曲线变化最平缓, 更贴近观测值曲线, 尤其在臭氧浓度变化幅度较小时段RF模拟值曲线与观测值曲线基本重合.
 |
| 图 3 决策树模型臭氧浓度模拟值及观测值时间序列图(图a~c分别表示CART、RF、M5模型树时间序列图, 图 1~4分别表示1、4、7、10月时间序列图) Fig. 3 Time series diagram of decision tree simulation and observation |
在决策树统计预报模型建模和验证基础之上, 进行区域臭氧浓度预报研究.首先需要获取区域气象预报数据, 研究中利用WRF模式气象预报场作为决策树统计预报模型输入, 预测徐州地区网格化臭氧浓度.以1、4、7、10月的15日中3:00、9:00、15:00、21:00四个时刻的第三层嵌套区域气象预测数据作为臭氧决策树模型输入, 得到臭氧浓度预报值, 模拟徐州市及其周边地区以上时刻的臭氧浓度空间分布特征.图 4~图 6分别为北京时间各月15日4个指定时刻的CART、RF和M5模型树模型研究区臭氧浓度的空间分布预测.图中圆形符号所在位置表示徐州市省控和市控大气监测站点.
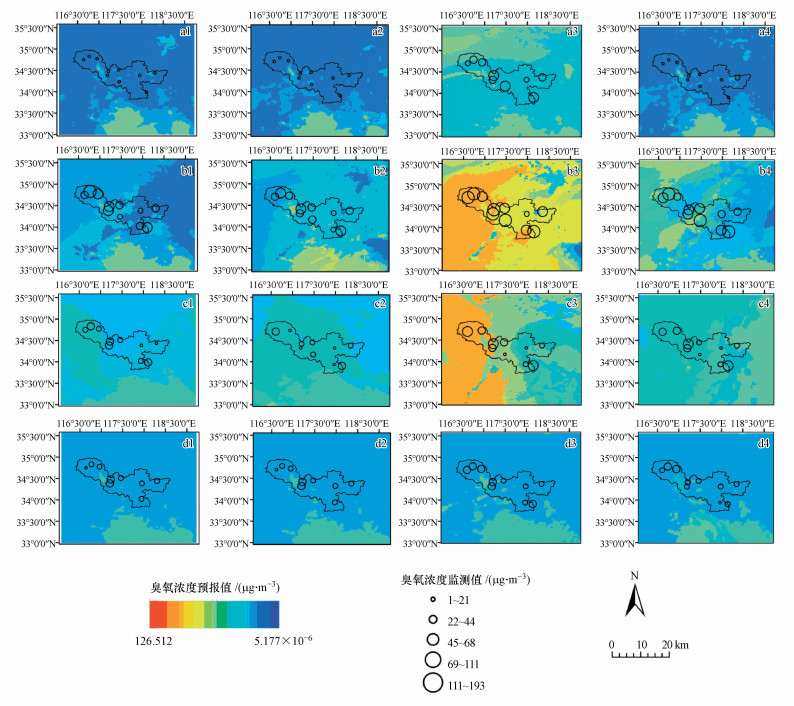 |
| 图 4 CART臭氧预测分布(a~d分别表示1、4、7、10月, 1~4表示北京时间3:00、9:00、15:00、21:00臭氧分布图, 背景浓度为臭氧浓度) Fig. 4 Distribution of CART ozone prediction |
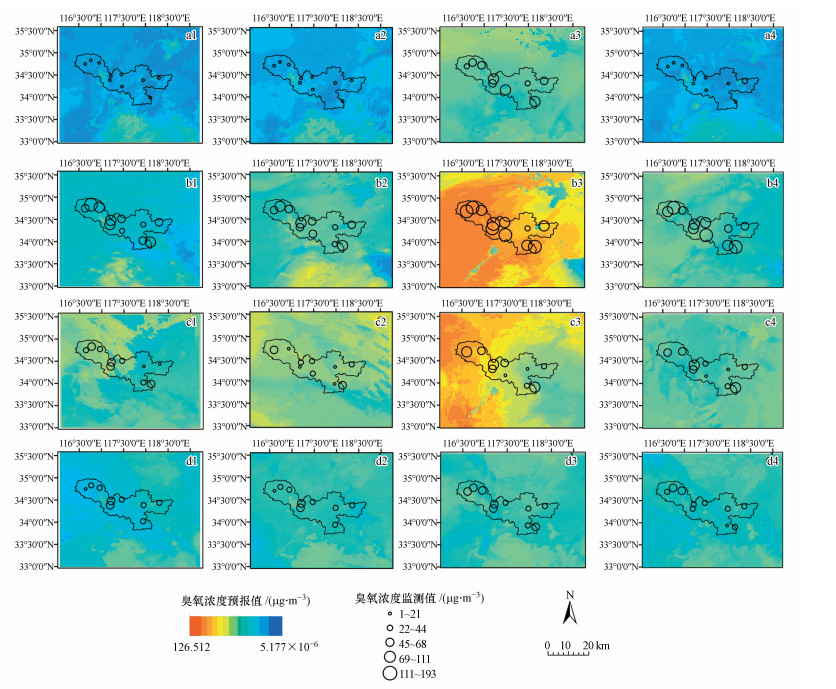 |
| 图 5 RF臭氧预测分布(a~d分别表示1、4、7、10月, 1~4表示北京时间3:00、9:00、15:00、21:00臭氧分布图, 背景浓度为臭氧浓度) Fig. 5 Distribution of random forest ozone prediction |
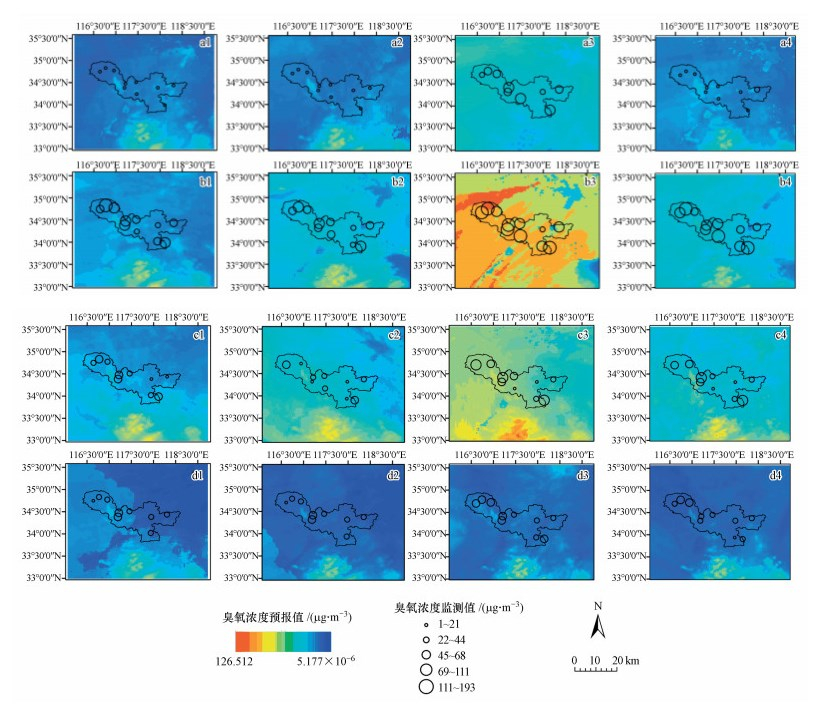 |
| 图 6 M5模型树臭氧预测分布(a~d分别表示1、4、7、10月, 1~4表示北京时间3:00、9:00、15:00、21:00臭氧分布图, 背景浓度为臭氧浓度) Fig. 6 Distribution of M5 model tree ozone prediction |
3种模型预报臭氧浓度空间分布和强弱动态变化特征相似.与站点观测臭氧浓度对比显示, 总体上预报结果较好地反映了臭氧浓度大小的时空分布特征, 4、7月徐州市臭氧浓度明显高于1、10月份, 且1月臭氧浓度最低, 3:00及15:00臭氧浓度分别为全天最大值及最小值时刻;徐州市西部和南部臭氧浓度显著高于东部和北部地区.这与区域内主要工业排放源分布密切相关.与调查资料对比发现该区域内泗城镇凤还巢创业园、大营工业园、郑集镇工业园区等多个工业园区分布着相当数量的药品厂、皮革厂、纺织厂、橡胶厂等污染物排放企业.徐州地区臭氧浓度分布空间上具有从南向北和从西向东逐渐扩散的特征:9:00之前太阳辐射较弱时段除徐州市正南和西南部外, 区域内臭氧浓度整体处于较低水平;9:00后随着太阳辐射的增强, 光化学反应速率加快, 臭氧浓度显著上升, 在15:00达到最高, 特别是在南部和西南部出现大片连续高臭氧浓度区域;21:00则明显减小且与3:00预报结果相当.表明15:00后整个区域臭氧浓度开始下降, 凌晨3:00基本下降到日最低水平.变化特征与臭氧浓度时间序列图保持一致.
对比3种方法的预报结果进一步证实了图 3站点验证结果:3种模型臭氧浓度预报值的时空分布特征相似, CART模型的臭氧浓度的空间预报结果呈明显块状分布, RF模型的输出结果变化最平缓, M5模型树的预报结果在局部地区有较大幅度变化.统计预报模型在1、7、10月对臭氧浓度普遍高估, 4月普遍低估, 且在15:00模型臭氧浓度最大值小于观测值.例如1月15日3:00站点臭氧浓度最小值为3 μg·m-3, CART预报浓度最小值为18.93 μg·m-3, RF为15.97 μg·m-3, M5模型树为10.93 μg·m-3, 均大于观测值最小值.15:00站点浓度最大值为101 μg·m-3, CART最大值为61.12 μg·m-3, RF为67.86 μg·m-3, M5模型树为52.31 μg·m-3, 均小于观测最大值.
本研究通过对监测站点处臭氧浓度预报值的误差统计分析对模型预报精度进行评估.如图 7国控站点臭氧浓度预报值验证泰勒图所示, 散点多数分布于相关系数为0.6的射线周围, 且4月和10月多数站点预报值和观测值相关系数大于0.6, 表明决策树模型在各站点处均可较好预测臭氧浓度的变化趋势.1月和4月预报值的标准偏差均小于1, 而7月和10月预报值散点大部分分布于弧线1上方, 即模型在1月和4月的预报值普遍小于观测值, 7月和10月普遍高于观测值.1月和10月CART预报值偏差较小, 其余两个月3种模型预报精度相近.
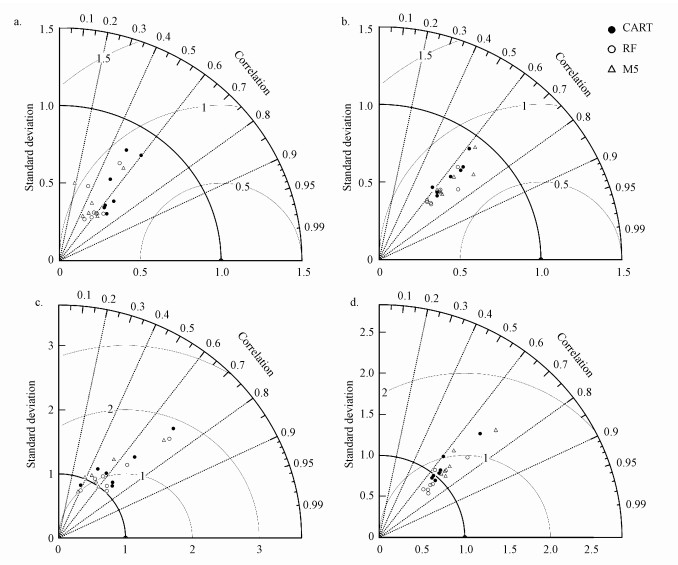 |
| 图 7 臭氧预报值验证泰勒图(图a~d分别表示1、4、7、10月精度验证图) Fig. 7 Taylor diagram of ozone forecast value verification |
如表 3所示, 进一步对决策树模型各月15—21日国控、省控和市控站点处臭氧浓度逐小时预报值与观测值对比分析.模型预报值与观测值的相关系数均值为0.58, 表明3种模型在4个月均可较好预测臭氧浓度变化趋势;其中4月和10月模型对于臭氧浓度的变化趋势的预报效果更好, 3种模型预报值与观测值相关系数均值为0.61.1、4和10月模型预报值绝对平均误差在30 μg·m-3以下, 均方根误差在40 μg·m-3以下;7月预报值精度较低, 预报值与观测值绝对平均误差的均值为46.37 μg·m-3, 均方根误差的均值为58.15 μg·m-3, 该月份臭氧预报值准确率均在75%以上, 其余月份预报值准确率均高于90%.CART和RF模型在4个季度均达到了相对较稳定的臭氧浓度预报结果, 相对而言, M5模型树稳定性较差, 不同月份预报值精度差别较大.
| 表 3 臭氧预报值与观测值对比 Table 3 Comparison of ozone forecast and observation |
由图 8模型预报值与观测值时间序列图分析可知, 总体而言, 模型预报值与观测值浓度变化趋势保持一致, 模型在1月和4月臭氧高污染时刻预报值仍小于观测值, 而显著高估7月及10月臭氧浓度.且根据图 4~图 6臭氧浓度空间预报分析, 7月15日9:00臭氧浓度的预测浓度异常偏高.导致此预测偏差的主要原因为, 臭氧统计预报模型的预测精度很大程度上依赖于WRF模式输出的气象预报数据的准确度, 在该研究中, WRF模式7月和10月的温度预报值普遍高于观测值, 相对湿度低于观测值.在温度较高, 相对湿度较低的气象条件下容易引发臭氧高浓度污染事件, 所以由于该时段WRF模式的气象场数据存在较大偏差, 导致决策树模型普遍高估臭氧浓度.
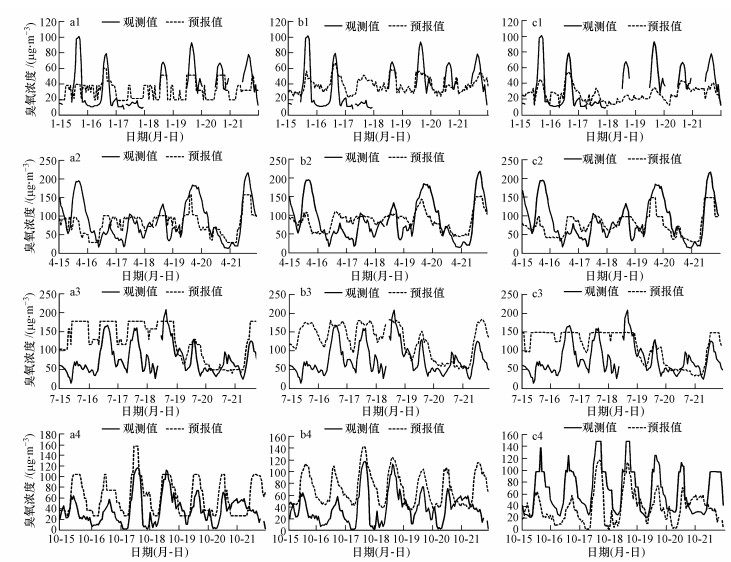 |
| 图 8 决策树预报值及观测值时间序列图(图a~c分别表示CART、RF、M5模型树时间序列图, 图 1~4分别表示1、4、7、10月时间序列图) Fig. 8 Time series diagram of decision tree forecast and observation |
通过模型验证、模型预报误差分析及臭氧浓度空间分布模拟效果分析, RF模型效果最佳, CART模型次之, M5模型模拟效果稳定性较差.其原因在于CART决策树算法是根据训练样本仅得到一棵庞大的描述臭氧浓度与气象因子之间关系的决策树, 其输出值为所有达到叶节点样本的平均值;M5模型树则以达到叶节点的样本建立回归方程, 以此得到模型输出;RF算法通过划分训练样本建立多棵决策树, 预测时通过专家投票综合决策树森林的所有预测结果得到最终的预测值, 因此不同模型对臭氧浓度与气象因子间的关系刻画的程度不同, 得到预测结果也有所差别.
由于决策树模型预报值存在普遍低估高污染时刻臭氧浓度的情况, 且对7月和10月臭氧浓度普遍高估, 因此依据多模式集合预报的原理, 利用待修正的24个时刻的前7 d徐州市7个国控大气监测站点逐小时监测数据及模型预报值建立多元回归方程, 并以待修正时段模型预报值作为输入, 以此滚动修正该站点上述4个月臭氧浓度预报值.将不同决策树模型预报值与观测值进行组合, 即取CART和RF模型预报值、M5模型树和RF预报值以及3种模型预报值, 分别与观测值建立多元线性回归方程, 实验结果表明, 由于M5模型树的预报结果稳定性欠佳, 故利用CART和RF模型预报值与观测值建立多元线性回归集合预报方程可达到最好的修正效果.
多模式集合修正效果如图 9所示, 修正后预报值精度得到明显的提升, 臭氧浓度极大值和极小值时刻的预报偏差明显降低.多模式集合预报对10月臭氧浓度预报值的修正效果最佳, 3种决策树在10月对臭氧浓度的预报普遍偏高(图 8), 多模式集合修正方法降低臭氧预报值浓度, 从而提高预报值精度.其余月份的修正效果主要表现在对臭氧浓度极小值时刻预报值的降低和极大值时刻预报值的提升.因此, 基于多元线性回归的多模式集合预报相对单个模型预报更具优势.
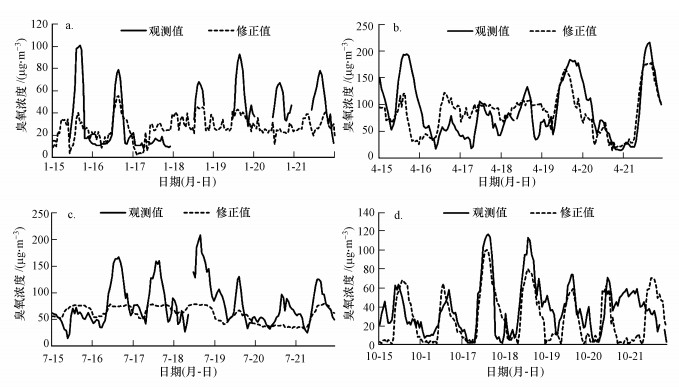 |
| 图 9 臭氧多模式集合修正值时间序列图(图a~d分别表示1、4、7、10月时间序列图) Fig. 9 Time series diagram of prediction modified by ozone multi-models ensemble |
表 4中经多元线性回归的多模式集合预报法修正的臭氧浓度预报值的误差统计结果显示修正后预报值与观测值相关系数均值为0.60, 与修正前预报值的相关系数相比有小幅度提高;1月和4月修正值的平均绝对误差与单个模型预报值的整体误差水平基本一致, 7月和10月修正的平均绝对误差明显小于单个模型预报值, 其中7月预报值偏差最大, 修正后预报值的平均绝对误差降低值28.34 μg·m-3, 且该月预报准确率也有所提升.图 10为多模式集合预报修正的臭氧浓度空间分布特征图.与单个模型预报结果相比, 多模式集合预报结果在一定程度上更贴近观测值, 特别是臭氧浓度极值时刻预报结果显著高于3种模型预报结果, 与观测值的偏差更小.通过以上分析表明, 多模式集合预报修正可在一定程度上提高模型的预报能力.
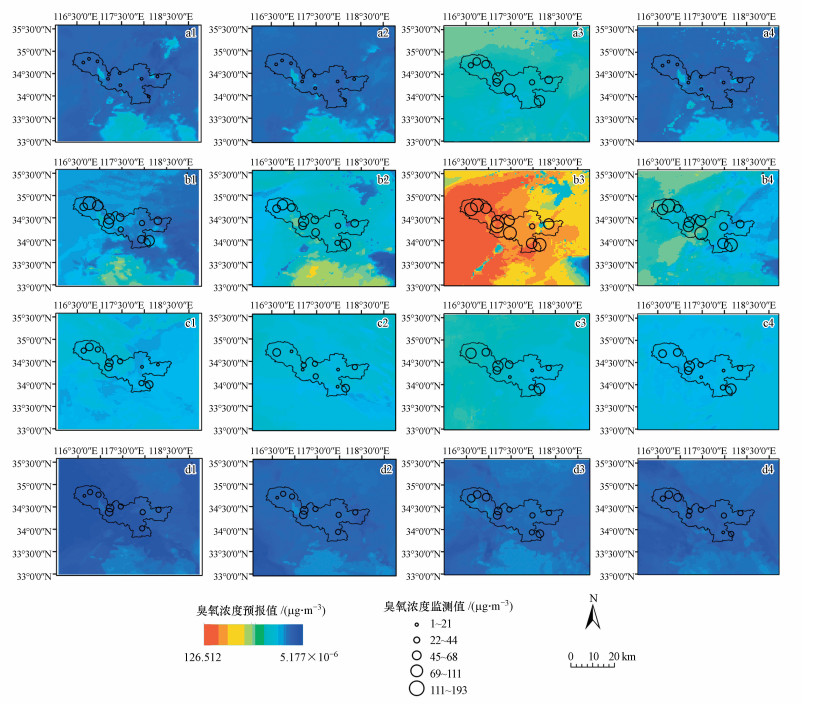 |
| 图 10 多模式集合修正分布(a~d分别表示1、4、7、10月, 1~4表示北京时间3:00、9:00、15:00、21:00臭氧分布图, 背景浓度为臭氧浓度) Fig. 10 Distribution of random forest ozone prediction |
| 表 4 臭氧多模式集合修正值与观测值对比 Table 4 Comparison of ozone forecast value modified by multi-models ensemble and observation |
不同气象要素对统计预报模型预测臭氧浓度的影响大小具有显著差异, 研究中在决策树模型臭氧浓度预测基础之上进一步分析各气象要素对臭氧浓度预测的重要性.CART模型变量重要性以权重的形式衡量, 因子的权重越大表示该因子影响臭氧浓度的能力越强.如表 5所示温度、相对湿度、气压、降水量、X向和Y向风权重重要性依次为45、34、15、5、1和1, 表明温度和相对湿度对CART模型预测臭氧浓度影响最大, 其次为气压和降水, 风速和风向则影响较小.
| 表 5 CART预测臭氧浓度的气象要素重要性 Table 5 Importance of each metrology factors in CART model |
RF模型利用节点不纯度平均减少量描述变量重要性, 某因子使节点不纯度降低的程度越大, 该因子越重要(Breiman, 2001;李亭等, 2014).图 11显示了RF模型预测臭氧浓度中6种气象要素重要性分析结果, 可看出温度的节点不纯度平均减少量最大, 其次是相对湿度、气压、降水量及风向.这一结果与CART模型和已有研究结论一致(王宏等, 2011;姚青等, 2009):即温度因子与臭氧浓度的相关性最强, 这是由于紫外辐射加强气温升高, 氧分子的分解得以增强, 且提高臭氧形成的光化学反应速率, 从而导致臭氧浓度升高;其次是相对湿度, 由于空气中的水汽为自由基与臭氧的反应创造了良好的环境, 在空气相对湿度较大的时候, 臭氧的浓度会有所降低;降水量和风要素则对臭氧浓度的变化影响较小.
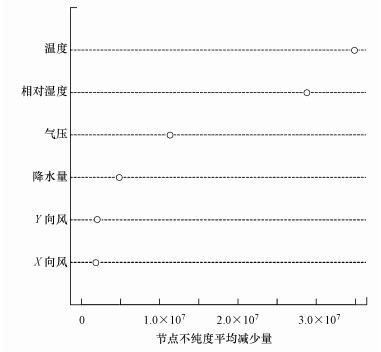 |
| 图 11 RF预测臭氧浓度的气象要素重要性 Fig. 11 Importance of each metrology factors in random forest model |
1) 3种决策树算法均可较好地模拟和预报研究区内臭氧浓度变化特征, 但对于臭氧极大值时刻模拟值明显偏低.对比3种算法的决策树模型, CART和RF模型预测效果较稳定, RF预测值变化平缓, 对污染物的变化趋势刻画的更细致.预测值准确度差异在于模型算法原理的不同.
2) 徐州地区臭氧浓度呈明显的自南向北和自西向东递减和扩散特征, 日臭氧浓度峰值时段为15:00左右.
3) 采用线性回归集成方法对3种模型预测结果进行修正后的集合预报臭氧浓度结果显著优于单个模型模拟结果, 尤其是极值时段臭氧浓度模拟得到明显改善.
4) 温度和相对湿度是影响臭氧浓度的主要因素, 其次为气压, 降水量和风对臭氧浓度影响较小.
5 展望(Prospect)本文研究表明CART、RF和M5模型树建立统计预报模型方法在区域臭氧浓度预报模拟中具有较好的应用价值.下一步工作主要考虑除了目前使用的风速风向和气压等因子外, 增加自变量因子包括扩散系数、污染物干沉降和湿沉降、混合层高度、大气稳定度及地面形势等(Businger et al., 1971;Carl et al., 1973;黄晓娴等, 2012).
Breiman L. 2001. Random forest[J]. Machine Learning, 45: 5–32.
DOI:10.1023/A:1010933404324
|
Breiman L, Friedman J, Olshen R, et al. 1984. Classification and Regression Trees. Belmont, CA:Wadsworth International Group[J]. Biometrics, 40(3): 582–588.
|
Businger, Wyngaard, Izumi Y I, et al. 1971. Flux-profile relationship in the atmospheric surface layer[J]. Journal of the Atmospheric Sciences, 28(2): 181–189.
DOI:10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2
|
Carl D M, Tarbell T C, Panofsky H A. 1973. Profiles of wind and temperature from towers over Homogeneous Terrain[J]. Journal of the Atmospheric Sciences, 30(5): 788–794.
DOI:10.1175/1520-0469(1973)030<0788:POWATF>2.0.CO;2
|
Debry E, Mallet V. 2014. Ensemble forecasting with machine learning algorithms for ozone, nitrogen dioxide and PM10 on the Prev'Air platform[J]. Atmospheric Environment, 91: 71–84.
DOI:10.1016/j.atmosenv.2014.03.049
|
Durão R M, Mendes M T, João Pereira M. 2016. Forecasting O3 levels in industrial area surroundings up to 24 h in advance, combining classification trees and MLP models[J]. Atmospheric Pollution Research, 7(6): 961–970.
DOI:10.1016/j.apr.2016.05.008
|
Jing-Hui M A, Lei-Ming M A, Geng F H, et al. 2012. Study on statistical forecast method for O3 concentration near the ground in pudong district of shanghai based on meteorological condition analysis[J]. Meteorological & Environmental Research(12): 54–59.
|
Michalakes J, Dudhia J, Gill D, et al. 2004. The weather research and forecast model: Software architecture and performance. Use of High Performance Computing in Meteorology[M]. World Scientific. 156-168
|
Quinlan J R. 1992. Learning With Continuous Classes[Z]. 343-348
|
安俊琳, 王跃思, 朱彬. 2010. 主成分和回归分析方法在大气臭氧预报的应用——以北京夏季为例[J]. 环境科学学报, 2010, 30(6): 1286–1294.
|
常明, 刘晓环, 刘明旭, 等. 2016. 非采暖期和采暖期青岛市及中国东部臭氧和细颗粒物模拟研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(2): 14–25.
|
郭晓雷. 2011. 城市空气质量预报方法研究综述[J]. 科技传播, 2011(15): 14–19.
|
黄思, 唐晓, 徐文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(1): 56–64.
|
黄晓娴, 王体健, 江飞. 2012. 空气污染潜势-统计结合预报模型的建立及应用[J]. 中国环境科学, 2012, 32(8): 1400–1408.
|
蒋璐璐, 钱燕珍, 杜坤, 等. 2016. 宁波市近地层臭氧浓度变化及预测[J]. 气象与环境学报, 2016, 32(1): 53–59.
DOI:10.11927/j.issn.1673-503X.2016.01.008 |
李亭, 田原, 邬伦, 等. 2014. 基于RF方法的滑坡灾害危险性区划[J]. 地理与地理信息科学, 2014(6): 25–30.
|
刘烽, 徐怡珊. 2017. 臭氧数值预报模型综述[J]. 中国环境监测, 2017, 33(4): 1–16.
|
刘闽, 王帅, 林宏, 等. 2014. 沈阳市冬季环境空气质量统计预报模型建立及应用[J]. 中国环境监测, 2014(4): 10–15.
|
沈劲, 王雪松, 李金凤, 等. 2011. Models-3/CMAQ和CAMx对珠江三角洲臭氧污染模拟的比较分析[J]. 中国科学:化学, 2011(11): 1750–1762.
|
宋榕荣, 王坚, 张曾弢, 等. 2012. 厦门市空气质量臭氧预报和评估系统[J]. 中国环境监测, 2012, 28(1): 27–32.
|
孙峰. 2004. 北京市空气质量动态统计预报系统[J]. 环境科学研究, 2004, 17(1): 70–73.
|
王宏, 林长城, 陈晓秋, 等. 2011. 天气条件对福州近地层臭氧分布的影响[J]. 生态环境学报, 2011, 20(Z2): 1320–1325.
|
王茜, 伏晴艳, 王自发, 等. 2010. 集合数值预报系统在上海市空气质量预测预报中的应用研究[J]. 环境监控与预警, 2010, 2(4): 1–6.
|
杨昕, 李兴生. 1999. 近地面O3变化化学反应机理的数值研究[J]. 大气科学, 1999, 23(4): 427–438.
|
姚青, 孙玫玲, 刘爱霞. 2009. 天津臭氧浓度与气象因素的相关性及其预测方法[J]. 生态环境学报, 2009, 18(6): 2206–2210.
|
章国材. 2004. 美国WRF模式的进展和应用前景[J]. 气象, 2004(12): 27–31.
|
周广强, 耿福海, 许建明, 等. 2015. 上海地区臭氧数值预报[J]. 中国环境科学, 2015, 35(6): 1601–1609.
|
 2018, Vol. 38
2018, Vol. 38


