2. 中国环境科学研究院, 国家环境保护地下水污染模拟与控制重点实验室, 北京 100012;
3. 上海大学环境与化学工程学院, 上海 200444;
4. 暨南大学地下水与地球科学研究院, 广州 510632
2. State Environmental Protection Key Laboratory of Simulation and Control of Groundwater Pollution, Chinese Research Academy of Environmental Science, Beijing 100012;
3. Environmental and Chemical Engineering College, Shanghai University, Shanghai 200444;
4. Institute of Groundwater and Earth Sciences, Jinan University, Guangzhou 510632
《中国海洋21世纪议程》指出, 中国沿海省、自治区、直辖市陆地面积约占全国国土面积的5%, 而其人口却占全国人口总数的40%以上.并且据2018年中国大、中城市固体废物污染环境防治年报统计, 城市生活垃圾产量排行前10的城市中沿海地区城市占一半.沿海地区城市垃圾填埋场地下水环境质量极差的比例较高, 未采取防渗措施的非正规垃圾填埋场渗滤液含有高浓度氨氮, 对地下水易造成污染风险(Han, 2011; Han et al., 2014).尽管氨氮不具备致癌风险, 但通过皮肤接触、呼吸等暴露接触, 可能导致眼睛、皮肤和呼吸道组织及器官损伤, 影响机体正常生理功能(Hoz et al., 2010; Davidson et al., 2017).因此, 预测填埋场发生泄漏后地下水氨氮污染过程, 判断地下水污染控制方案是否有效, 具有重要科学研究意义.
迄今为止, 许多学者对地下水氨氮污染特征做了大量研究.杨洋等(2014)利用HYDRUS-1D模型模拟垃圾填埋场渗滤液中的氨氮在包气带中的迁移转化规律, 该研究用预测的源强值来评价场地污染程度, 最终预测出氨氮到达地下水位处时的浓度值, 为场地污染防控和治理提供数据参考.Jellali等(2010)通过室内土柱实验和计算机模拟程序研究氨氮在土壤中的迁移转化过程, 结果表明土壤对氨氮的吸附满足线性等温吸附关系.Zuo等(2017)将修正的DRTCLN模型应用于氨氮的观测分布, 对区域地下水污染风险进行了评价, 分析了西北干旱黄土平原地区地下水氨氮浓度升高的成因和污染风险, 并对评价结果进行了不确定性分析, 结果表明, 地下水源区大部分地区的风险值相对较低, 只有南部地区一个工业区被列为高风险区.国内外在地下水氨氮污染过程研究方面具有一定研究基础, 但大多数研究仅局限于非饱和带, 针对于饱和带的氨氮污染研究较少; 研究多限于室内土柱实验, 野外实际场地验证研究较少.
海积平原是指由于海浪搬运淤积等因素使海积物形成的平原地形, 通常是人口相对密集的地区(Sefelnasr et al., 2014), 其浅层地下水埋深浅, 地下水含盐量高、流速低, 易受到污染(雷抗等, 2018), 但海积平原区填埋场渗滤液氨氮泄漏污染过程相关研究较少(Wang et al., 2012).因此, 本研究针对我国海积平原区某填埋场, 依据海积平原区实际气象、水文、地质条件, 利用Modflow和MT3DMS程序构建了地下水氨氮运移模型, 分析了氨氮在浅层地下水中的时空分布特征和迁移规律, 在此基础上进行抽出处理污染控制方案模拟, 为海积平原区填埋场地下水污染防治提供理论与实践参考.
2 研究区概况与方法(Survey and methods of research area) 2.1 研究区概况研究区位于华北平原东北部, 属于黄骅冲海积滨海低平原区, 具体位于中国天津市, 距海岸线大约48 km(图 1).研究区属暖温带半湿润性大陆季节型气候, 区内地势平坦, 微向东倾, 海拔高度由北向南一般为2 ~1 m, 属海积、冲积平原, 地表全为第四系、无基岩出露.
 |
| 图 1 研究区位置 Fig. 1 Location of the study area |
该填埋场占地约160000 m2, 是附近居民生活垃圾的接纳场所, 没有防渗、渗滤液处理等基础环保设施, 存在地下水环境安全隐患.为了获得地层建模数据以及垃圾填埋场可能影响深度, 掌握研究区域地层分层、填埋场渗漏情况, 在填埋场及周边施工工程钻孔20个(图 1), 钻孔围绕在填埋场的外围布置, 同时兼顾填埋场区域地下水的上下游布置, 并且进行物探勘查.通过物探数据的处理, 结合钻孔资料及调查情况, 得到研究区各含水层岩性特征、顶底板高程.填埋场浅部地层大致分为3层:①第一层岩性主要为粉土、杂填土、回填垃圾, 层厚为10~15 m.②第二层岩性主要为粉质粘土, 层厚为5~10 m.③第三层岩性主要为细砂, 层厚为7~10 m.研究区未发现粉砂透镜体贯穿粉质粘土的渗漏通道.
2.2 地下水流模拟 2.2.1 概念模型研究区地下水人工开采量很小, 区域内地下水在天然状态下水流坡度不大, 地下水以水平运动为主, 流速缓慢, 渗流符合达西定律.自然介质通常是非均质的.在实际应用中, 岩性相似的相邻含水层常合并为一个含水层, 含水层的分层主要基于研究区水文地质勘察结果, 且研究区含水层岩性变化不大, 水文地质参数根据钻孔信息分区.水文各要素随时间发生变化, 将其最终概化为非均质各向异性的三维非稳定流模型.在垂向上, 潜水含水层自由水面为该地下水系统的上边界, 通过该边界与系统外发生垂向交换.水平方向上, 由于地势最低, 且受周边坑塘影响, 垃圾填埋场南侧靠中的位置地下水水位较低, 潜水含水层的地下水整体呈现轻微西北向东南的趋势, 东部与西部边界与区域地下水流向大致平行, 因此定为零流量边界处理.研究区由于不是一个完整的水文地质单元, 没有完整的自然边界(如地表水、地下水分水岭等), 可将其概化为人为边界, 即定流量边界, 边界侧向流量可用达西定律计算.
2.2.2 地下水控制方程基于质量守恒定律的基础上, 本研究水流控制方程和定解条件如下所示:
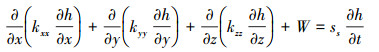
|
(1) |
定解条件:
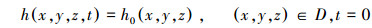
|
(2) |
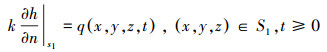
|
(3) |
式中:h为水头(L); kxx, kyy, kzz分别kxx, kyy, kzz为x、y、z方向的渗透系数(L · T-1); W为流体的源/汇项, 即流进(正值)或流出(负值)单位体积含水层的体积流量(T-1); ss为单位储水量, 即水头下降单位值时单位体积含水层释放出的水的体积(L-1); h0为初始水头值, 即初始时刻研究区D内各点(x, y, z)处的水头(L-1); S1为Neumann边界条件, 即已知边界面上的流量q, n为边界S1的外法线方向; 隔水边界流量为0.
2.2.3 数值模拟为了准确刻画模拟区, 在上述水文地质概念模型建立的基础上, 本研究利用MODFLOW建立了地下水流动模型, 采用有限差分的离散方法剖分网格, 并对垃圾填埋场区域、定流量边界的有限差分网格细化2倍, 垂向上剖分为5层, 共有35行, 55列, 5层, 共11550个单元.模拟周期为2017年9月1日—2018年8月31日, 以3个月为一个应力周期, 以应力周期中的天数为时间步长.
此外, 大气降水是该区地下水的重要补给来源, 模型中降水入渗量按面状补给量处理.降水量取天津市气象局记录的多年平均降水量.研究区浅层地下水埋深为1.5~2 m, 蒸发比较强烈, 是浅层潜水含水层主要排泄途径之一.水流模型的解法选择有稳定解、收敛快的WHS解法(Olsthoorn, 1999).地下水数值模拟中水文地质参数是非常重要的, 其合理性与正确性将直接影响地下水模型的准确性及可信度, 根据抽水试验, 进行渗透系数的分区, 其他参数的初始值采用相应岩性的给水度、储水率、有效孔隙度的经验值.根据经验数据, 水平渗透系数设为其垂向渗透系数的10倍.
2.3 污染物运移模拟 2.3.1 污染物运移控制方程基于氨氮在地下水中的迁移性质, 本研究选用的溶质运移控制方程(Zheng et al., 1999)为:
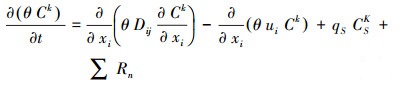
|
(4) |
定解条件为:
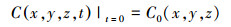
|
(5) |
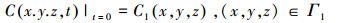
|
(6) |
式中, θ为地下介质的孔隙度, 无量纲; Ck为物质k的溶解浓度(M · L-3); t为时间(d); Dij为水动力弥散系数张量(L2 · T-1); ui为孔隙水流实际速度(L · M-1); qS为单位体积含水层源(正值)和汇(负值)的体积流量(T-1); Csk为源汇流中物质k的浓度(M · L-3); ∑Rn为化学反应项(M · L-1); C0为初始浓度; C1(x, y, z)为Dirichlet边界条件, 即给定浓度边界函数; Γ1为研究区D的第一类边界.
2.3.2 数值模拟溶质运移模型中对流项选择隐式GCG解法, 并选择MT3DMS模型运行(Zheng et al., 2011), 以面状污染源形式设定垃圾填埋场浓度边界, 污染源位置按实际设计概化, 网格剖分加密两倍.由于不同的研究场地和不同的研究条件下各个参数的取值也会相差很大, 为了更准确地描述本研究区的氨氮运移过程, 本次溶质运移模拟的参数参考了前人的研究成果, 纵向弥散度的计算参考Gelhar等(1992)的观测尺度和纵向弥散度之间的经验关系, 此项研究中各层横向/纵向弥散度比率为0.1, 垂向/纵向弥散度比率为0.01.本研究中假设地层对氨氮的吸附满足线性等温吸附关系(Jellali et al., 2010).
3 结果与讨论(Results and discussion) 3.1 模型校正与敏感性分析综合考虑研究区水文地质抽水实验以及经验参数, 并通过2017年9月—2018年8月8口监测井的计算水位和实际水位拟合分析, 运用试错法进行模型校正, 反复调整参数, 最终得到了水流模型参数(表 1).通过拟合分析水位模拟值与实测值, 模拟地下水位与实测水位之间存在一定的偏差, 其中8个校正井的最大水头误差为0.25 m、平均绝对误差(MAE)值为0.08 m(误差均小于10%), 均方差根误差(RMSE)小于0.03 m, 这些误差相对于监测井最大水位变化值1.8 m较小.从整体上看, 校准后的地下水流模型能较好地反映地下水的真实水力系统, 模拟结果与实际地下水流量系统的模拟结果较为接近, 表明水流模拟结果可靠.
| 表 1 地下水流模型参数 Table 1 Groundwater flow model parameters |
为了分析垃圾填埋场对周边地下水环境造成的影响, 基于校正过的水流模型, 结合上述设置, 利用MT3DMS模型模拟了地下水中氨氮的时空分布.通过将计算得到的氨氮浓度与2017年9月—2018年8月8口监测井实测的氨氮浓度进行比较, 对模型进行了校正, 以符合研究区地下水实际污染情况.溶质运移模型的主要校正参数为弥散系数和吸附系数.图 2为实测氨氮浓度与模拟数据的校正图, 8个监测井的观测浓度与计算浓度之间的平均绝对误差(MAE)值为0.78 mg · L-1, 均方根误差(RMSE)值为0.35 mg · L-1.这些误差相对于监测井最大浓度变化值2.3 mg · L-1较小.总的来说, 模拟的氨氮浓度与观测值吻合较好.从中可以看出, 地下水氨氮运移模型的校正结果的准确性是可以接受的.建立的溶质运移模型能够反映真实的水文地质条件和地下水中氨氮浓度, 因此, 校准后的模型可以预测地下水中氨氮浓度的变化.
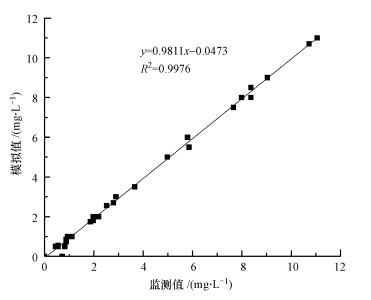 |
| 图 2 氨氮浓度校正 Fig. 2 Correction of ammonia nitrogen concentration |
由于目前仅在潜水含水层中发现氨氮污染现象, 并且该含水层的渗透性相对较高, 其参数变化对地下水氨氮运移模拟的影响比其它含水层更大(Chang et al., 2018), 所以仅选取潜水含水层进行敏感性分析.在用数值法进行地下水溶质迁移模拟时, 渗透系数、孔隙度、弥散度均为重要的参数(Zheng et al., 2002).
本文在建立溶质迁移数值模型的基础上, 运用因子变换法分析了地下水溶质迁移模型中渗透系数、孔隙度和弥散度等参数的变化对模拟结果的影响, 发现在与介质有关的参数中, 污染物迁移距离对渗透系数和孔隙度最为敏感, 而孔隙度的敏感性指数略高于渗透系数; 弥散度对迁移距离的影响最小, 其敏感性指数与渗透系数、孔隙度相差一个数量级(图 3), 即渗透系数和孔隙度的改变对溶质迁移距离的影响远大于弥散度, 而流速又是有效孔隙度和渗透系数的函数(Zheng et al., 2002), 所以这很有可能是因为研究区地下水中氨氮运移主要是对流在起作用, 弥散的作用很小所致.
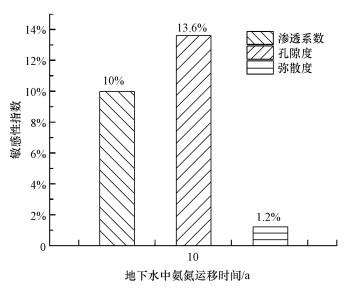 |
| 图 3 地下水模型参数的敏感性指数 Fig. 3 Sensitivity index of groundwater model parameters |
根据地下水流模型预测结果(图 4), 由于研究区地势平坦, 且浅层地下水为咸水无法饮用及农业灌溉, 目前基本无开发利用, 故水位总体上基本稳定.浅层地下水位动态主要受大气降水的影响, 多年水位动态特征基本与气象周期一致, 通过地下水流模型预测结果显示(图 4a), 高水位出现在汛期的9—10月, 而低水位出现在4—5月, 其余月份较为稳定.由于区域浅层地下水水位埋深较浅, 蒸发量较大, 主要补给源来自大气降水, 含水层渗透性较差, 水力坡度很小且径流十分缓慢, 来自上游的侧向径流补给量是微乎其微的, 其水位动态类型属于渗入-蒸发型, 研究区地下水位随时间呈缓慢下降趋势.根据研究区地下水流场图(图 4b), 潜水含水层中的地下水整体呈现轻微西北向东南的趋势.由于地势最低, 且受周边坑塘影响, 垃圾填埋场南侧靠中的位置地下水位较低.
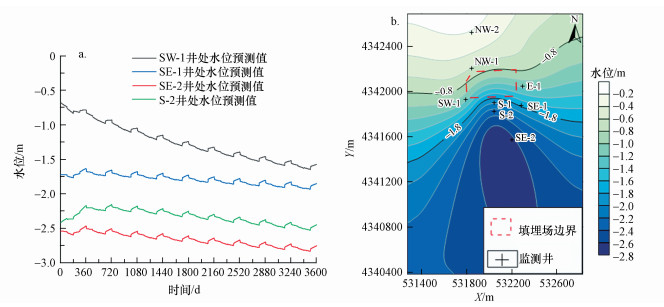 |
| 图 4 地下水流模拟 (a.监测井水位预测值, b.研究区地下水流场) Fig. 4 Groundwater flow simulation (a. Predicted value of monitoring well water level, b. Groundwater flow field in the research area) |
基于上述校正过的溶质运移模型进行地下水污染预测, 根据预测结果得出地下水对高浓度的渗滤液起到十分重要的稀释作用, 同时也使得地下水中氨氮的浓度大幅上升, 该垃圾填埋场中氨氮主要沿流向污染东南部地下水, 填埋场以南200 m范围内污染程度最高, 污染物浓度距离污染源越远其浓度越低, 氨氮污染羽在10年内最大迁移距离为648 m, 污染面积达到368667 m2(图 5).
 |
| 图 5 10年后潜水含水层污染物运移趋势 Fig. 5 The trend of pollutant migration in unconfined aquifer after 10 years |
为了防止垃圾渗滤液进一步污染周边地下水, 根据溶质运移模型结果以及研究区地层情况, 设计并选择最有效的地下水修复控制方案.地下水抽出处理技术是地下水污染场地修复中使用最为广泛的技术.该技术可以快速改变地下水流动速度和方向, 并且能够改变地下水污染羽的扩散方向与范围(An et al., 2013).结合敏感性分析结果, 研究区污染物运移主要受对流作用影响, 因此, 本研究从切断污染路径角度出发, 在地下水污染羽下游S-1井南部设置3个抽提井.根据污染羽的扩散范围以及场地抽水试验资料, 抽提井的抽水率设置为100 m3 · d-1来模拟抽出处理的效果(图 6a).
 |
| 图 6 抽出处理方案效果模拟 (a.地下水流场, b.S-1井处氨氮浓度) Fig. 6 Effect simulation of extraction treatment scheme (a. Groundwater flow field, b.Ammonia nitrogen concentration at S-1 well) |
该方案模拟预测结果(图 6b)表明抽出处理方案能够很快降低含水层中氨氮的浓度, 该抽出处理方案在抽水初期阶段能够有效去除含水层中大量污染物质, 并且减缓了污染羽的扩散范围和速度, 预测结果显示在600多天后浓度就能降到1 mg · L-1, 但当停止抽水后, 污染物释放转为由扩散控制的状态后, 含水层中污染物浓度还是会逐渐升高, 在1000 d后停止抽水后, 潜水含水层中氨氮浓度开始逐步升高.
地下水抽出处理导致污染拖尾反弹的原因可能有以下几点:①垃圾渗滤液渗入到地下含水层后, 经过一段时间扩散到相对渗透性较差的孔隙介质中, 而抽出的污染的地下水大部分来自多孔介质含水层中渗透性较好的区域, 因此抽出处理方案效果不佳; ②地下水流速慢的区域污染物被滞留的可能性更大, 且脱附和溶解效应较为明显, 低流速含水层污染物的扩散作用是产生拖尾和反弹效应的重要因素(蒲敏, 2017); ③根据雷抗等(2018)的上下游土壤阳离子交换量数据, 分析得出土壤可能吸附了大量的氨氮.当地下水中污染物浓度降低时, 由于浓度梯度的驱动, 岩层中吸附的污染物又逐渐溶解进入地下水中.当进行抽出处理时, 地下水快速流动, 溶解效应不明显, 停止抽出处理之后, 地下水流速变缓, 非溶解相污染物与地下水接触时间增加, 溶解现象更为明显, 造成反弹现象.
拖尾和反弹效应是地下水抽出处理技术中常见的问题, 也是地下水难以处理达标的重要障碍(蒲敏, 2017), 并且研究区地下水埋深较浅, 流速较慢, 浅层含水层介质渗透性较弱.经抽水实验验证, 使用抽水泵抽出15 m深浅层地下水, 2~3 h后井管中地下水即被抽干, 且24 h后地下水水位才能恢复, 地下水异位处理抽水效率低、抽水周期长、地面运行维护成本高, 所以抽出处理方案不能彻底降低研究区地下水氨氮浓度.
4 结论(Conclusions)海积平原区某非正规垃圾填埋场对南部区域的地下水环境造成了污染, 若不采取任何污染控制措施, 氨氮污染羽在10年内最大迁移距离为648 m, 污染面积达到368667 m2, 高浓度氨氮污染羽主要分布于南部浅层潜水含水层.水文地质参数中孔隙度和渗透系数对溶质迁移计算结果影响较大.抽出处理能够很快降低含水层中氨氮的浓度, 但停止抽水后, 潜水含水层中氨氮浓度开始逐步升高, 出现地下水污染反弹现象.原位修复技术更适用于该填埋场地下水污染治理.
An D, Jiang Y, Xi B, et al. 2013. Analysis for remedial alternatives of unregulated municipal solid waste landfills leachate-contaminated groundwater[J]. Frontiers of Earth Science, 7(3): 310–319.
|
Chang Y, Hu B.X, Xu Z, et al. 2018. Numerical simulation of seawater intrusion to coastal aquifers and brine water/freshwater interaction in south coast of Laizhou Bay, China[J]. Journal of Contaminant Hydrology, 215: 1–10.
|
Davidson M E, Schaeffer J, Clark M L, et al. 2017. Personal exposure of dairy workers to dust, endotoxin, muramic acid, ergosterol and ammonia on large-scale dairies in the high plains western United States[J]. Journal of Occupational & Environmental Hygiene, 15(3): 182–193.
|
Gelhar L W, Welty C, Rehfeldt K R. 1992. A critical review of data on field-scale dispersion in aquifers[J]. Water Resources Research, 28(7): 1955–1974.
|
Han D, Tong X, Currell M.J, et al. 2014. Evaluation of the impact of an uncontrolled landfill on surrounding groundwater quality, Zhoukou, China[J]. Journal of Geochemical Exploration, 136: 24–39.
|
Hua H. 2011. Preliminary survey and assessment of unregualted landfill sites[J]. Journal of Engineering Geology, 50(4): 60–64.
|
Hoz R E, De La, Schlueter, et al. 2010. Chronic lung disease secondary to ammonia inhalation injury: a report on three cases[J]. American Journal of Industrial Medicine 29(2): 209-214.
|
Jellali S, Diamantopoulos E, Kallali H, et al. 2010. Dynamic sorption of ammonium by sandy soil in fixed bed columns:Evaluation of equilibrium and non-equilibrium transport processes[J]. Journal of Environmental Management, 91(4): 897–905.
|
雷抗, 李瑞, 李鸣晓, 等. 2018. 海积平原区浅层地下水污染在线监测预警指标的确定-以天津市某简易生活垃圾填埋场为例[J]. 环境工程, 2018, 36(11): 179–184.
|
Olsthoorn T N. 1999. A comparative review of analytic and finite difference models used at the Amsterdam Water Supply[J]. Journal of Hydrology, 226(3/4): 139–143.
|
蒲敏. 2017. 污染场地地下水抽出处理技术研究[J]. 环境工程, 2017, 35(4): 6–10.
|
Sefelnasr A, Sherif M. 2014. Impacts of Seawater Rise on Seawater Intrusion in the Nile Delta Aquifer, Egypt[J]. Groundwater, 52(2): 264–276.
|
Jiabing W, Ping L, Baiming Z. 2010. Allowable groundwater withdrawal and its determination basis in Tianjin Plain[J]. Earth Science Frontiers, 17(6): 221–226.
|
杨洋, 李娟, 李鸣晓, 等. 2014. HYDRUS-1D软件在地下水污染源强定量评价中的应用[J]. 环境工程学报, 2014, 8(12): 5293–5298.
|
Zheng C M, Bennett G D, Zheng C M, et al. 2002. Applied contaminant transport modelling[J]. Eos Transactions American Geophysical Union, 77(48): 908–923.
|
Zheng C, Bianchi M, Gorelick S M. 2011. Lessons learned from 25 years of research at the MADE site[J]. Ground Water, 49(5): 649–662.
|
Zheng C, Wang P P. 1999. MT3DMS:A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User's Guide[J]. Ajr American Journal of Roentgenology, 169(4): 1196–1197.
|
Zuo R, Chen X, Li X, et al. 2017. Distribution, genesis, and pollution risk of ammonium nitrogen in groundwater in an arid loess plain, northwestern China[J]. Environmental Earth Sciences, 76(17): 629.
|
 2019, Vol. 39
2019, Vol. 39


