叶绿素a浓度是可直接遥感反演的重要水质参数之一, 常用来评价水体的富营养化程度(宋挺等, 2017).叶绿素a浓度的遥感反演主要有经验方法、半分析方法和分析方法3类(Morel et al., 1980), 其中, 经验方法相对简单、易行, 是目前应用最为广泛的反演方法, 因此, 本文采用经验方法反演叶绿素a浓度.
在传统经验方法中, 一般通过单波段或不同波段的组合来估测叶绿素a浓度, 但与一类水体中叶绿素a成为单一主导光学因子不同, 二类水体是由叶绿素a、悬浮颗粒物、黄色物质等多种光学因子共同主导(陈瑜丽等, 2016), 光谱特征与水体组分浓度之间的关系并不能完全采用简单线性反演模型来表示(IOCCG, 2000; 刘阁, 2016).当前, 机器学习方法逐渐被引入到二类水体叶绿素a浓度反演中, 该类型的方法是通过多次拟合, 实现输入与输出之间的高度非线性映射关系.机器学习方法具备自适应、自组织性和较高的容错性, 在数据分析上具有适用范围广、可靠性强等优点(毕顺等, 2018), 是提高二类水体叶绿素a浓度估算精度的一种重要思路.神经网络算法(谢旭等, 2018; Chen et al., 2014; 曹红业等, 2016)对噪声数据具有较强容错性和鲁棒性, 但也存在参数较多、学习时间长且需要大量的样本数据等不足(张玉超等, 2009).实地测量因受多种条件的限制, 采集的数据量较少, 因此, 适用于小样本数据建模的随机森林方法(张明慧等, 2018)被用于反演二类水体叶绿素a浓度.随机森林方法是使用“随机”决策树, 只需检查一个属性子集, 随着个体学习器数目的增加, 随机森林会收敛到更低的泛化误差(周志华, 2016), 具有较好的鲁棒性(Hua et al., 2018).为建立适合于闽江下游的叶绿素a反演模型, 本文选用不同的方法构建模型, 以确定最优的闽江下游叶绿素a浓度反演模型, 为闽江下游水环境的监测提供一定的理论依据和技术参考.
GF-1卫星是中国自主研发的高分辨率对地观测系统首发星, 其高分辨率和较高的时间分辨率能满足精细尺度水质持续监测的要求.闽江是福建省最长的河流, 水体中叶绿素a、悬浮物浓度比较高, 属典型的二类水体.因此, 本文以闽江下游为研究对象, 基于水面采样数据, 选择多元回归方法、BP神经网络与随机森林方法构建闽江下游叶绿素a浓度反演模型, 对比分析不同模型的反演结果, 并使用国产空间分辨率为16 m的GF-1 WFV遥感影像, 对模型的遥感反演精度进行评估.
2 研究区与数据(Study area and data) 2.1 研究区概况本研究选择闽江下游闽侯白沙以东至琅岐岛西作为研究区(图 1), 地理范围为25°57′~26°13′N, 119°01′~119°35′E, 水体流经闽侯县、福州主城区、马尾区和琅岐岛西部.该区属亚热带海洋性季风气候类型, 气候温和, 雨量充沛, 周边土地利用类型以城镇建设用地、林地为主.从地图上可知, 研究区河道宽度最大值为4526 m, 最小值为182 m.本研究使用空间分辨率为16 m的GF-1 WFV影像, 河道的最小宽度远大于影像的单个像元, 因此, 河流光谱受沿岸环境的影响较小.
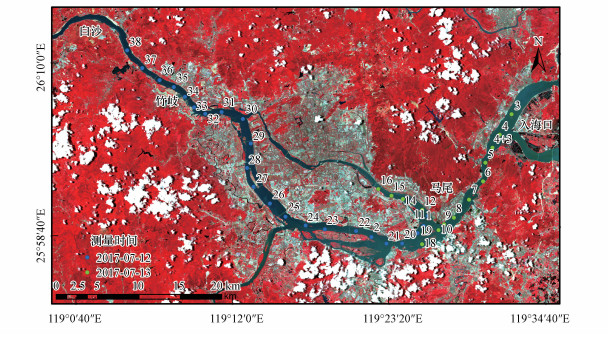 |
| 图 1 研究区域概况(底图为2017年7月11日的GF-1 WFV1影像标准假彩色图像) Fig. 1 Study area (The bottom image is the standard false color image of GF-1 WFV1 image on July 11, 2017) |
2017年7月12—13日10:00—15:00, 在闽江上总共设置40个采样点.在每个采样点上进行光谱测量并同步进行水质采样, 同时利用GPS记录每个采样点的WGS-84坐标.采样当天, 天空晴朗、水面平静, 光谱测量采用ISI921VF-512野外地物光谱辐射计, 测量方法选用水面以上测量方法(唐军武等, 2004).同步水质采样在光谱测量点水面之下20~30 cm处, 叶绿素a浓度采用L5S紫外可见分光光度计测定, 悬浮物浓度采用重量法(GB 11901-89)测定.闽江下游实测的叶绿素a浓度最大值为26.1 mg·m-3, 最小值为1.81 mg·m-3, 平均值为11.481 mg·m-3;悬浮物浓度最大值为37 mg·L-1, 最小值为12 mg·L-1, 平均值为22.75 mg·L-1, 3种典型的不同叶绿素a浓度实测光谱如图 2所示.
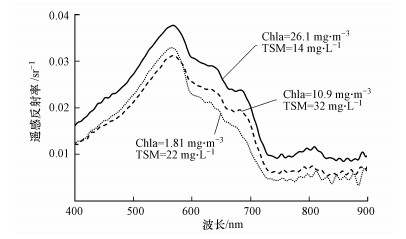 |
| 图 2 实测光谱曲线 Fig. 2 Measured spectral curves |
由于卫星过境前后天气良好无大雨, 水量稳定, 可以接受卫星过境时间和采样时间相隔2 d的误差.因此, 选择与野外采样时间准同步的2017年7月11日GF-1 WFV1影像数据, 对构建的叶绿素a反演模型进行遥感精度验证, 其搭载的WFV传感器参数见表 1.
| 表 1 GF-1 WFV传感器参数 Table 1 Parameters of GF-1 WFV sensor |
本文利用野外采集的实测光谱和叶绿素a浓度数据分别建立多元回归、BP神经网络和随机森林模型, 并对比分析3种模型结果.同时, 对GF-1 WFV影像数据进行预处理与水体提取.将处理后的影像应用于训练好的模型反演闽江下游叶绿素a浓度, 最后对模型的遥感反演精度进行评估.具体技术流程图如图 3所示.
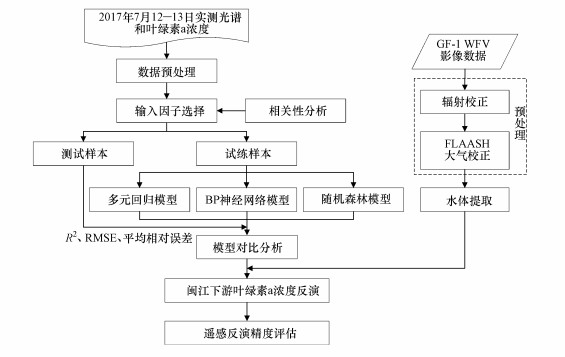 |
| 图 3 技术流程图 Fig. 3 Technical flow chart |
先对野外采集的实测光谱进行预处理, 将实测光谱按照公式(1)转化为GF-1 WFV1可见光和近红外波段设置光谱反射率.
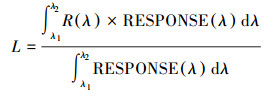
|
(1) |
式中, R(λ)为实测水体反射率, RESPONSE(λ)为GF-1 WFV1传感器的波段响应函数, λ1和λ2分别表示波段范围的下界和上界, L为传感器波段总辐射率.
对获取的影像利用ENVI软件进行影像预处理, 使用ENVI自带的FLAASH模块对影像进行大气校正.水体反射在第1、2波段(B1、B2)较多, 在第3(B3)和第4波段(B4)大多吸收, 纯净水体在第1波段出现反射峰, 含叶绿素的清水在第2波段出现反射峰.图 4给出了水体在大气校正前后的光谱曲线对比图, 可以看出, 大气校正后, 去除了大气的干扰, 光谱曲线有了明显变化, 光谱更加接近真实的水体光谱.
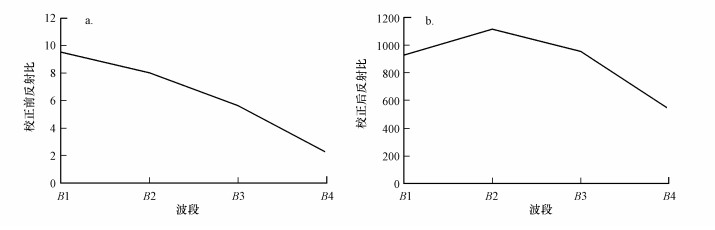 |
| 图 4 水体大气校正前后光谱曲线对比(a.校正前; b.校正后) Fig. 4 Comparison of water spectrum curves before (a) and after (b) atmospheric correction |
采用单波段建立的叶绿素a浓度估算模型往往不能很好地反映影响因子与水质参数之间的关系, 因此, 本文对实测光谱预处理后获得的GF-1 WFV1波段进行组合, 分别与Chla、lg(Chla)进行Pearson相关性分析.结果显示, lg(Chla)与GF-1 WFV1波段及波段比值组合的相关系数比Chla大.波段比值中, B1/B3、B2/B3、B3-B1的相关性较好, 相关系数都高于0.80(表 2).为保证测试样本分布的合理性, 将40份特征因子和叶绿素a浓度数据按递增方式均匀选取10份样本用于模型检验, 剩余30份作为训练样本, 同时选用B1/B3、B2/B3、B3-B1波段组合作为输入因子分别建立多元回归模型、BP神经网络模型和随机森林模型.
| 表 2 GF-1 WFV1波段及组合与lg(Chla)的相关系数 Table 2 Correlation coefficients of GF-1 WFV1 bands and its combination with lg(Chla) |
根据3.1节相关性分析结果, 将输入因子作为多元回归模型的自变量, 建立闽江下游叶绿素a浓度多元回归反演模型, 得到的多元回归模型公式如下:

|
(2) |
式中, B1、B2、B3分别为GF-1 WFV影像的第1、2、3波段.
3.3 BP神经网络BP(Back Propagation)神经网络也称误差逆向传播神经网络, 由Rumelhart和McClelland提出, 是目前所有人工神经网络应用最为广泛的(王磊等, 2016).BP神经网络具有自适应性、高学习能力和强容错能力等特点, 具有偏差和至少一个S型隐含层加上线性输出层的网络, 能够逼近任何有理函数(朱云芳等, 2017).
本文构建一个3层结构的BP神经网络模型, 选择进行过标准化的输入因子作为输入层, 叶绿素a浓度作为输出层, 选取tansig作为激活函数, 训练采用贝叶斯正则化算法的trainbr函数.设置最大训练次数为10000, 训练速率为0.05, 训练误差为1×10-4, 其余参数为默认值.隐含层结点的确定是神经网络模型的关键步骤, 目前尚未有研究给出统一的算法, 通过多次试验确定隐含层的最佳节点数为8.
3.4 随机森林随机森林(Random Forest)是Bagging的一个扩展变体, 在以决策树为基学习器构建Bagging集成的基础上, 进一步在决策树的训练过程中引入了随机属性选择(Cutler et al., 2004).在建模过程中, 随机森林只需输入两个参数, 即决策树的数目NTREE和基于决策树的每个结点的自变量数目MTRY, 并且每个参数对自身变化不敏感(Palczewska et al., 2014), 这一优势有利于叶绿素a浓度的预测.
建模过程可以分为3步:构建输入训练数据集、训练预测模型和叶绿素a浓度预测.首先, 将进行过标准化的输入因子作为随机森林的特征因子参与建模, 训练样本作为训练数据集, 验证样本作为测试数据集;在训练过程中, 根据MTRY= m(m为输入特征数)分别将1、2作为MTRY的备选输入值, 选用评价指标决定系数(R2)和均方误差(MSE)通过网格搜索法确定参数NTREE和MTRY的最优值(NTREE=280, MTRY=1)(图 5), 通过训练数据集训练得到叶绿素a浓度反演模型;最后, 反演获得叶绿素a浓度空间分布, 并使用测试数据集评估模型性能和精度.
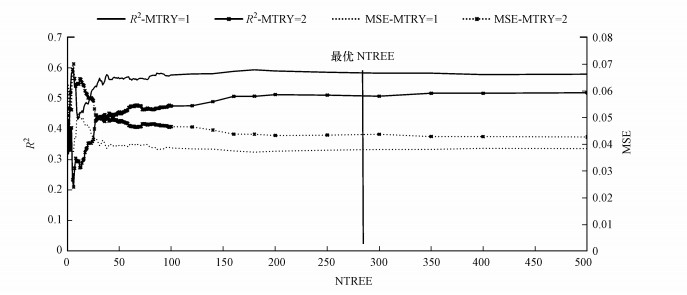 |
| 图 5 参数NTREE和MTRY的最优值 Fig. 5 Optimal values for parameters NTREE and MTRY |
由表 3可知, 随机森林模型的可决系数R2为0.895, 均方根误差RMSE为1.994 mg·m-3, 平均相对误差为11.502%, 是3种模型中RMSE和平均相对误差最小、R2最高的, 其中, 随机森林模型验证样本中相对误差最小值为2.498%, 最大值仅为31.715%;BP神经网络模型相对误差最小值为4.519%, 最大值为40.203%;多元回归模型相对误差最小值为0.572%, 最大值为127.168%.当多元回归模型验证样本点的相对误差较大时, BP神经网络和随机森林模型都能很好地控制这种误差, 使得其相对误差较小.相同的输入特征和训练数据条件下, 多元回归模型的精度最低, 因为该模型只是简单地对数据进行了拟合;BP神经网络模型则利用梯度搜索技术, 经过自适应和容错性等过程, 使实测值与预测值之间的误差最小, 但其样本量过少会影响其精度;而随机森林作为有效的非线性建模方法, 适用于小样本数据, 能在建模过程中进行参数优化, 并且能很好地学习特征波段和叶绿素a浓度之间的关系, 提高模型的预测精度.总体上, 随机森林模型是3种模型中估算闽江下游叶绿素a浓度最优的.
| 表 3 不同模型叶绿素a浓度反演结果对比分析 Table 3 Comparison and analysis of chlorophyll-a concentration inversion results in different models |
基于2017年7月11日GF-1 WFV1影像数据, 根据构建的BP神经网络和随机森林模型反演闽江下游叶绿素a浓度, 结果如图 6所示.从图 6可以看出, 叶绿素a浓度的总体分布都表现为从白沙往入海口方向逐渐增加, 且两种模型估测的叶绿素a浓度分布大致相同.白沙到竹岐段, 叶绿素a浓度范围为0~4 mg·m-3, 这是因为河岸两边大部分是植被, 水体较为清澈并未受污染, 因此, 叶绿素a浓度较低.竹岐到马尾段, 叶绿素a浓度逐渐增加, 这是因为该段进入福州主城区, 工农业生产及人类生活废水中含有大量的氮、磷、钾等营养物质, 这些废水排入到水体当中, 使得水体处于富营养状态(李洪山等, 2002).水中浮游植物特别是藻类等水生生物大量生长繁殖, 而浮游植物和藻类的主要色素就是叶绿素a(Mandalakis et al., 2017).其中, 随机森林模型估算的叶绿素a浓度略高于BP神经网络模型.马尾到入海口, 叶绿素a浓度高于竹岐到马尾段, 这是由于南北港两大支流的汇合所导致.BP神经网络模型估算的叶绿素a浓度在该段区域明显低于随机森林模型.入海口琯头附近, BP神经网络和随机森林模型预测的叶绿素a浓度都呈现出小幅下降趋势, 这是因为在入海口琯头附近有污水处理厂, 使得水中的叶绿素a浓度减少.
 |
| 图 6 不同模型反演叶绿素a浓度 Fig. 6 Different models inversion of chlorophyll-a concentration |
在影像上的白沙、竹岐、马尾、入海口和琯头5个区域, 分别获取对应实测点位上模型预测的叶绿素a和实测叶绿素a浓度, 并对其相对误差和RMSE进行计算, 结果见图 7.由图可知, 随机森林模型的相对误差与RMSE从白沙到琯头大致都是呈上升趋势, BP神经网络模型的趋势则较为不稳定.其中, 随机森林模型在38号、34号和19号实测点的相对误差与RMSE均小于BP神经网络, 在4号和3号点, 结果则相反.因为样本数据量较少, 所以BP神经网络模型的稳定性较差, 但适合于小样本预测的随机森林模型在入海口和琯头附近预测效果较差, 不能很好地估算该区域复杂的叶绿素a浓度变化.
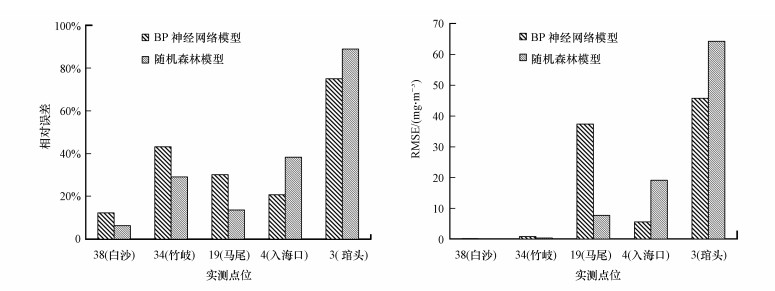 |
| 图 7 不同模型预测值与实测值之间的相对误差与RMSE Fig. 7 The relative error and RMSE between predicted and measured values of different models |
为评估模型遥感反演的精度, 提取野外实测点对应的像元反射率, 获得BP神经网络与随机森林模型遥感估算的叶绿素a浓度, 剔除因影像预处理出现异常值的实测点, 总计36个模型估算的叶绿素a浓度, 将其与实测叶绿素a浓度进行对比分析, 结果如图 8所示.
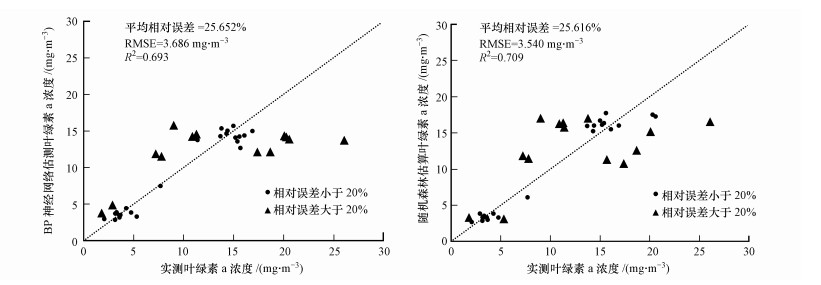 |
| 图 8 叶绿素a遥感反演精度评价 Fig. 8 Evaluation of the accuracy of chlorophyll-a remote sensing inversion |
由图 8可知, 两种模型的反演精度相差较小, 随机森林模型估算的叶绿素a与实测叶绿素a浓度之间的R2为0.709, RMSE为3.540 mg·m-3, 平均相对误差为25.616%;BP神经网络模型的R2为0.693, RMSE为3.686 mg·m-3, 平均相对误差为25.652%.实测叶绿素a在低值范围内, 两种模型都能够较准确地估算出该区的叶绿素a浓度;在叶绿素a浓度中值区, 两种模型估测的叶绿素a浓度值都偏高, 该区域相对误差大于20%的点的悬浮物浓度范围为23~32 mg·L-1, 估算的叶绿素a浓度值偏高与高悬浮物浓度的强散射作用有关;高值区结果相反, 两种模型估测的叶绿素a浓度值都偏低, 相对误差大于20%的点的悬浮物浓度范围为18~24 mg·L-1, 估算的叶绿素a浓度值偏低是因为中悬浮物浓度对离水辐亮度的作用, 导致模型存在低估叶绿素a浓度的趋势(毛志华等, 2006).总体上, 随机森林模型遥感反演的结果精度较好, 进一步说明构建好的随机森林模型在遥感影像上的适用性较好.为验证闽江下游随机森林模型反演叶绿素a浓度的准确性和全面性, 应在研究区域内获得更多时相的实测数据, 验证模型在不同时相上遥感反演的适用性.
5 结论(Conclusions)1) 本文基于2017年7月12—13日闽江下游的实测光谱和叶绿素a浓度同步测量数据, 结合GF-1 WFV遥感影像数据, 对各波段及波段组合与叶绿素a浓度和lg(Chla)进行相关性分析, 结果证明, 波段组合B1/B3、B2/B3、B3-B1与lg(Chla)的相关系数均高于0.8, 可作为多元回归、BP神经网络和随机森林3种模型的输入特征.
2) 对比各模型的相对误差、RMSE及R2, 结果表明, 基于GF-1 WFV影像的随机森林模型反演闽江下游叶绿素a浓度是最优的, BP神经网络与随机森林模型的精度接近, 较多元回归模型的精度高.当多元回归模型验证样本点的相对误差较大时, BP神经网络和随机森林模型都能很好地控制这种误差.基于BP神经网络和随机森林模型, 利用GF-1 WFV1遥感影像进行叶绿素a浓度反演, 结果显示, 两者反演的空间分布规律相似, 闽江下游叶绿素a浓度的空间分布总体都表现为西低东高, 从白沙往入海口方向逐渐增加.
3) 对模型的遥感反演结果进行精度评价, 可知构建好的随机森林模型在遥感影像上的适用性较好.随机森林和BP神经网络模型在估算叶绿素a浓度时, 估算值与实测值之间的误差与悬浮物浓度的作用有一定的关系.遥感反演的精度还与影像的大气校正有关, 精确的大气校正是水色遥感监测的前提, 之后的研究可加入其它大气校正方法作比较, 进一步分析对比不同方法的遥感反演精度.
毕顺, 吕恒, 朱利, 等. 2018. 基于OLCI数据的洱海叶绿素a浓度估算[J]. 湖泊科学, 30(3): 123-124. |
曹红业, 龚涛, 袁成忠, 等. 2016. 基于RBF模型的太湖北部叶绿素a浓度定量遥感反演[J]. 环境工程学报, 10(11): 6499-6504. DOI:10.12030/j.cjee.201506134 |
Chen J, Quan W, Cui T, et al. 2014. Remote sensing of absorption and scattering coefficient using neural network model: Development, validation, and application[J]. Remote Sensing of Environment, 149: 213-226. DOI:10.1016/j.rse.2014.04.013 |
陈瑜丽, 沈芳. 2016. 长江口及邻近海域悬浮颗粒物对叶绿素a遥感反演算法的影响分析[J]. 遥感技术与应用, 31(1): 126-133. |
Cutler A, Cutler D R, Stevens J R. 2004. Random Forests[J]. Machine Learning, 45(1): 157-176. |
Hua S, Li W, Yan X H. 2018. Retrieving temperature anomaly in the global subsurface and deeper ocean from satellite observations[J]. Journal of Geophysical Research Oceans, 123(1): 399-410. DOI:10.1002/2017JC013631 |
IOCCG.2000.Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters[R].Dartmouth, Canada: IOCCG
|
李洪山, 黎松强. 2002. 水体富营养化的生化防治机理—污水深度处理与脱氮除磷[J]. 海洋科学, 26(6): 31-34. DOI:10.3969/j.issn.1000-3096.2002.06.010 |
刘阁.2016.适用于不同光学特征二类水体的叶绿素a浓度遥感估算方法研究[D].南京: 南京师范大学.147 http://cdmd.cnki.com.cn/Article/CDMD-10319-1017280146.htm
|
Mandalakis M, Stravinskait A, Lagaria A, et al. 2017. Ultrasensitive and high-throughput analysis of chlorophyll a in marine phytoplankton extracts using a fluorescence microplate reader[J]. Analytical and Bioanalytical Chemistry, 409(19): 4539-4549. DOI:10.1007/s00216-017-0392-9 |
毛志华, 朱乾坤, 龚芳, 等. 2006. CMODIS资料提取叶绿素a浓度的反演算法研究[J]. 海洋学报:中文版, 28(3): 57-63. |
Morel A Y, Gordon H R. 1980. Report of the working group on water color[J]. Boundary-Layer Meteorology, 18(3): 343-355. DOI:10.1007/BF00122030 |
Palczewska A, Palczewski J, Robinson R M, et al.2014.Interpreting Random Forest Classification Models Using a Feature Contribution Method[C].Proceedings of the 2013 IEEE 14th International Conference on Information Reuse and Integration (IRI).Palma de Mallorca: 112-119
|
宋挺, 周文鳞, 刘军志, 等. 2017. 利用高光谱反演模型评估太湖水体叶绿素a浓度分布[J]. 环境科学学报, 37(3): 888-899. |
唐军武, 田国良, 汪小勇, 等. 2004. 水体光谱测量与分析Ⅰ:水面以上测量法[J]. 遥感学报, 8(1): 37-44. |
王磊, 王汝凉, 曲洪峰, 等. 2016. BP神经网络算法改进及应用[J]. 软件导刊, 15(5): 38-40. |
谢旭, 陈芸芝. 2018. 基于PSO-RBF神经网络模型反演闽江下游水体悬浮物浓度[J]. 遥感技术与应用, 33(5): 900-907. |
张明慧, 苏华, 季博文. 2018. MODIS时序影像的福建近岸叶绿素a浓度反演[J]. 环境科学学报, 38(12): 4831-4839. |
张玉超, 钱新, 钱瑜, 等. 2009. 基于机器学习方法的太湖叶绿素a定量遥感研究[J]. 环境科学, 30(5): 1321-1328. DOI:10.3321/j.issn:0250-3301.2009.05.012 |
周志华. 2016. 机器学习:Machine Learning[M]. 北京: 清华大学出版社.
|
朱云芳, 朱利, 李家国, 等. 2017. 基于GF-1 WFV影像和BP神经网络的太湖叶绿素a反演[J]. 环境科学学报, 37(1): 130-137. |
 2019, Vol. 39
2019, Vol. 39


