2. 东北财经大学博士后科研流动站, 大连 116025
2. Post-Doctoral Mobile Station, Dongbei University of Finance and Economics, Dalian 116025
2017年, 中国碳排放量占全球碳排放量的27%, 居于全球首位.为积极应对全球气候变暖, 中国制定了“2030年实现全国碳排放达峰”目标.而城市是温室气体的主要排放源, 中国70%的碳排放来自城市(杨秀等, 2015).到2030年, 这一比例还将升至80%.抓住城市这个龙头, 也就抓住了控制排放的主体.可以说, 城市达峰排放, 有力支撑了中国乃至全球的绿色低碳发展.如果城市不能实现碳排放达峰, 全国就不可能在2030年前实现碳达峰.因此城市层面的碳达峰是实现中国碳达峰目标的必要条件.目前, 全国已经确定87个低碳试点省市, 其中有72个省市提出了自己的达峰目标.这些试点、超大城市积极探索绿色低碳发展模式及碳排放达峰路径, 在节能、提高能效、发展可再生能源等方面均走在了全国前列.不少城市虽然提出碳达峰目标, 但是还缺少清晰的达峰路线图, 各城市在保证经济发展的同时进行低碳转型需要向北京、上海、广州、深圳、天津和重庆等超大城市进行学习, 因此超大城市的碳达峰研究对国内其他城市的碳达峰有前瞻性启示意义.
学术界在城市碳排放问题研究上取得了一定的成果.日本学者kaya首次提出的kaya恒等式将CO2排放与人类活动联系起来, 由此产生的kaya分解法被广泛用于研究预测碳排放峰值(王金南等, 2010;邓宣凯等, 2014;杨秀等, 2015), 添加了其他相关的影响因素, 用协整方程预测未来CO2排放量(冯宗宪等, 2016), 而且一些研究使用蒙特卡洛模拟方法突破情景分析(叶玉瑶等, 2014)中的静态局限, 动态预测了CO2排放量变动(林伯强等, 2010).传统的环境库兹涅茨(EKC)曲线认为随着经济增长, 碳排放总量会呈倒“U”形.使用EKC模型并加入其它固定效应的扩展模型的学者通过城市碳排放拐点分析计算出了达峰时间(吴立军等, 2016;郑海涛等, 2016).部分已有研究使用评估未来CO2排放的LEAP模型估算了城市或部门的未来CO2排放量(Yu et al., 2015;Lin et al., 2018).IPAT模型(杜强等, 2012)虽有效地揭示环境压力与人类活动的各种驱动因素之间的关系, 但其中驱动因素弹性是相同的, 其随机形式-STIRPAT模型随之被开发并广泛应用.学者们在STIRPAT模型中加入了其他排放因子(王凯等, 2017), 被用于度量城市碳排放和各驱动因素之间的关系(黄蕊等, 2013;彭智敏等, 2018), 进行城市碳达峰预测(张乐勤等, 2013;刘晴川等, 2017;Wu et al., 2018;吴青龙等, 2018), 但其中驱动因素弹性是固定的.已有研究将Hansen(1999)提出的静态面板门限模型(the static panel threshold model)和STIRPAT扩展模型结合, 构成了门限-STIRPAT扩展模型(王泳璇, 2016;Dong et al., 2019).
已有研究在城市碳达峰方面有不少的成果, 但仍有几点不足:①碳排放因子对碳排放的阶段性影响有待明确.已有城市碳排放研究大多是10年以上的数据, 却忽略了城市碳排放因子对碳排放的影响是否存在阶段性变化, 可能会使碳排放研究存在偏差.②在城市碳排放的情景预测方面, 情景类型设定不够全面.已有文献大多使用情景分析法预测峰值, 但情景种类较少, 可能会导致碳达峰情况考虑不全面, 对城市实现碳达峰目标的指导作用较弱.基于已有研究存在的问题, 本研究提出了本文的研究思路:以北京、上海、广州、深圳、天津和重庆这6个超大城市为研究对象, 考虑了STIRPAT模型中常住人口、居民富裕程度和技术水平这3个碳排放驱动因素, 先利用静态面板门限模型根据能源强度的高低划分成几个阶段, 再利用门限-STIRPAT模型确定碳排放量与驱动因素之间的关系, 最后用情景分析确定不同情景下城市碳排放达峰时间和峰值大小.本文的创新点体现在以下几个方面:①本文首次将门限-STIRPAT模型应用于城市层面碳达峰研究, 考察碳排放驱动因素对城市碳排放的阶段性影响, 更加贴切地描述城市的发展对城市碳排放的影响变化.②本文将城市碳排放驱动因素变化率设定为3种强度(高、中和低)并排列组合, 建立27种组合情景进行预测, 为各城市碳达峰研究提供较为全面的情景考虑, 为相关政策制定提供更多思路.
2 模型构建(Model building) 2.1 门限-STIRPAT模型构建传统的STIRPAT模型由IPAT模型发展而来, 公式表示为式(1).
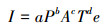
|
(1) |
式中, I、P、A和T分别表示区域的碳排放量、人口、经济发展水平和技术因素;a为模型系数;b、c、d分别为变量P、A、T的指数;e为模型误差项.
其对数形式为式(2):
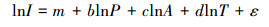
|
(2) |
式中, m=lna, ε=lne.
已有研究大多只研究了各个解释变量与碳排放量之间不变的关系, 而忽略了碳排放量在不同发展阶段和某解释变量并不是一种不变的因果关系, 而是会在某个特定时期该解释变量对碳排放的影响程度会发生改变.本文将STIRPAT模型与面板门限模型结合在一起, 人口和居民富裕程度作为控制变量;参考李国志(2011)认为技术对二氧化碳排放的影响呈阶段性变化特征, 将技术水平作为门限变量, 同时也作为受门限变量影响的解释变量, 构成门限-STIRPAT模型, 进而对城市碳排放量达峰进行预测.在实际应用中, 常以对数形式表示, 因此本文设定门限-STIRPAT模型(假设是单个门限)见式(3).
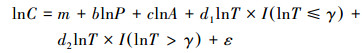
|
(3) |
式中, I(·)为示性函数, 相应条件成立时取1, 不成立时取0;为了与示性函数区分开, 用C表示城市二氧化碳排放量.
2.2 模型变量选择① 被解释变量:城市碳排放量用各地区化石能源消费(终端消费+中间投入)和调入电力产生的二氧化碳排放量表示, 单位为万吨, 用C表示.二氧化碳排放量的核算公式为式(4):
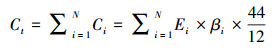
|
(4) |
式中, Ct表示t年消费的所有能源的CO2排放量, Ci表示第i种能源的CO2排放量, βi为该种能源的碳排放系数, Ei为能源消费量.其中, 公式(4)中能源的碳排放系数βi是参考将IPCC2006中的各种能源CO2排放系数根据我国热值调整得到的IPCC收录的各种燃料CO2排放系数表中的数值.
② 解释变量与控制变量:本文选取人口、居民富裕程度和技术水平作为门限-STIRPAT模型的控制变量.其中, 用地区常住人口表示人口(P), 单位为万人;用人均GDP表示居民富裕程度(A), 人均GDP是由地区生产总值除以常住人口得出(2005年不变价), 单位为元;用能源强度(万元生产总值能耗)表示技术水平(T), 单位为kg.选取能源强度为受门限变量影响的解释变量, 构成技术进步视角下的门限-STIRPAT模型.
③ 门限变量:本文选取表示技术水平的能源强度(T)作为门限变量.
3 情景设计及数据来源(Scenario design and data sources) 3.1 情景设计以中国以及各省、市《国民经济与社会发展第十三个五年计划纲要》中的发展目标和“十二五”期间的社会发展现状为基础, 本文设置了人口、人均GDP、能源强度3种因素的3种变化速率(低速率、中速率和高速率), 具体设定见表 1.
| 表 1 各城市CO2排放影响因素的情景参数设定 Table 1 Scenario parameter setting of factors affecting CO2 emissions in various cities |
人口的情景设计.到2020年, 北京、上海和天津的常住人口分别要求控制在2300万人、2500万人和1800万人以内, 广州的常住人口预期达到1550万人, 其他城市的常住人口数并无明确的预期性或约束性指标.将上述人口发展目标、“十二五”期间和2016年的实际人口增量比较, 控制人口的北京、上海和天津将最大值设定为高速, 最小值为中速, 以中高速差值和中低速差值相差不大为依据设定低速;广州的最小值设定为中速、最大值为高速, 深圳“十二五”期间实际人口增量设定为中速, 重庆的最小值为低速, 以±10的变化设定其余增速.由于人口增量设定结合了各城市发展现状和“十三五”规划, 尤其在非首都功能疏解背景下的北京人口增量高速不超过“十二五”期间年均增量, 意味着该设定具有现实可行性.
人均GDP的情景设计.北京市在“十三五”期间GDP预期年均增速6.5%左右, 重庆市GDP预期年均增速9%左右, 广州市预期年均增速7.5%左右, 上海市预期年均增速6.5%左右, 深圳市GDP预期到2020年达到26000亿元、人均GDP达到17.6万元, 天津市GDP预期年均增速8.5%左右.以“十二五”期间人均GDP年均增速为主要基础, 根据2016年增速和“十三五”预期进行必要调整, 北京和上海的人均GDP增速设其为中速, 以±0.5%的变化设定其余增速;重庆、广州和深圳设其为高速, 分别以±2%、±1%和±0.5%的变化设定其余增速;天津在相关基础上结合最严格环保制度新形势下调增速, 设定中高速差值和中低速差值为1%, 这也具有可行性.
能源强度的情景设计.广州市的单位地区生产总值能耗在“十三五”期间计划累计降低19.3%, 其他5个城市则计划累计降低国家制定的目标15%.以各个城市或国家的“十三五”规划和“十二五”期间发展现状为基础, 将其最值设定为能源强度下降率可取的范围, 并以±0.5%的变化来缩小, 得到能源强度变化速率的临界值(只要能源强度下降速率高于低速, 就会出现能够达峰的情景;只要低于高速, 达峰情景数就会减少很多), 设定为能源强度变化速率的最终范围, 中速则取其中间值, 并且这样在实际中容易实现.
为了全面考虑各城市的发展方向、更加谨慎地预测城市碳达峰情况, 本文将人口、人均GDP和能源强度的3种变化率进行排列组合, 总共考虑了27种情景, 按能源强度下降速率分组, 如表 2所示.
| 表 2 27种情景设定说明 Table 2 27 scenario setting instructions |
北京、重庆、上海、天津等4个城市的能源消费数据(实物量)来源于《中国能源统计年鉴》地区能源平衡表, 广州和深圳的能源消费数据通过对应省份的能源消费数据估算得到.城市碳排放量根据《中国能源统计年鉴》中除其他能源以外的原煤、洗精煤、其他洗煤、汽油等各种化石能源的消费量(中间投入和终端消费量的总和)和调入电力的量计算.能源消费总共包括了《中国能源统计年鉴》中除其他能源以外的原煤、洗精煤、其他洗煤、汽油等各种化石能源、热力和电力的消费量(损失量和终端消费量的总和).能源各项系数参考《中国能源统计年鉴》附表和《IPCC国家温室气体排放清单指南2006》中的数据.碳排放量使用我国热值进行调整.人口、人均地区生产总值和间接计算广州和深圳的能源消费量时使用的数据均来自于各地区以及所属省份的统计年鉴数据, 缺失数据采用插值法或者前一年的增长率或增量确定.本文使用的经济数据均以2005年不变价表示.
4 模型检验结果分析(Model test result analysis) 4.1 平稳性检验为了避免伪回归, 需要对面板数据进行平稳性检验.对面板数据分别进行LLC和PP检验, 其检验结果如表 3所示.结果显示, 每个变量的检验统计量均显著, 即模型中的变量均平稳, 可以进行回归分析.
| 表 3 平稳性检验结果 Table 3 Stationarity test result |
能源强度作为模型的门限变量, 需要先进行门限效应检验, 从而确定门限效应是否存在以及门限的个数, 检验结果如表 4所示, 其中F统计量和p值通过Bootstrap方法(通常反复抽样300次)得到.门限变量能源强度在单重门限抽样的p值为0.07, 在10%显著性水平下显著, 故拒绝了线性模型的假设;在双重门限抽样的p值为0.78, 即使在10%显著性水平下也不显著, 所以拒绝了双重门限的假设;在三重门限抽样的p值为0.62, 在10%显著性水平下并不显著, 所以也拒绝了三重门限的假设.因此以能源强度为门限变量的门限-STIRPAT模型对应单重门限模型.
| 表 4 门限效应检验结果 Table 4 Threshold effect test results |
单重门限模型确定之后, 需进一步确定门限-STIRPAT扩展模型中的门限值.门限值和置信区间如表 4所示, 能源强度的门限值为403.43 kg, 即lnT等于6.00.
根据门限效应计算结果, 不同能源强度阶段下的门限-STIRPAT模型可以具体表示为式(5):
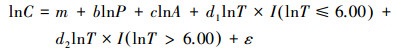
|
(5) |
分析上述结果可推测, 万元能耗处于403.43 kg前后时, 城市碳排放所受的影响有阶段性的变化.
4.3 门限-STIRPAT模型参数估计及分析根据上节对门限值的确定, 样本数据可以分成低技术水平阶段(T>403.43 kg)、高技术水平阶段(T≤403.43 kg)两个阶段.分组之后, 进一步进行差异性分析.用最小二乘法来估计模型参数, 估计结果见表 5.
| 表 5 门限-STIRPAT模型参数估计结果 Table 5 Model parameter estimation results |
单重门限下, 观察对样本的回归结果, 门限-STIRPAT模型的具体形式为式(6):
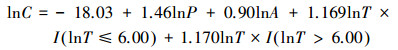
|
(6) |
在技术水平的两个阶段中, 常住人口和人均GDP对碳排放均为正效应且固定不变.常住人口弹性为1.46, 即常住人口数每增长1%, 碳排放量就会增长1.46%;人均GDP弹性为0.90, 即人均GDP每增长1%, 碳排放量就会增长0.90%.虽然在技术水平的不同阶段, 能源强度对碳排放的效应均为正, 但是两阶段的能源强度弹性不同.当能源强度低于403.43 kg时, 碳排放的技术水平弹性为1.169;当能源强度高于403.43 kg时, 弹性为1.170.无论是高能源强度水平还是低能源强度水平, 人口效应最大, 其次是能源强度(技术水平)效应, 最后是人均GDP(居民富裕程度)效应.
能源强度对二氧化碳排放的影响呈阶段性变化特征.由公式(6)可以得到, 能源强度低水平阶段的弹性比高水平阶段的弹性要小, 说明了能源强度越低, 越有利于城市碳排放量的减少, 促进城市碳排放尽快达峰.虽然能源强度效应不如人口效应, 但是分别加上能源强度变化率和人口变化率的影响(城市能源强度变化率是人口变化率的3~6倍), 会使得能源强度弹性和能源强度变化率的综合影响超过人口弹性和人口变化率的共同作用, 从而使碳排放尽快达峰, 这也体现了注重技术进步和开发清洁能源的重要性.
4.4 稳健性检验稳健性检验就是通过改变计量方法或者某些参数时, 进行重复的实验, 来观察实证结果是否发生变化, 如果不发生变化, 说明该模型并不是只适用于文中的样本数据, 证明模型具有稳健性.稳健性检验结果如表 6、表 7所示, 结果显示门限值和参数系数并不发生改变且均能通过显著性检验, 因此, 本文建立的模型具有稳健性.
| 表 6 稳健性检验后的门限效应检验结果 Table 6 Results of the threshold effect test after the robustness test |
| 表 7 稳健性检验后的模型参数估计结果 Table 7 Estimation results of model parameters after robustness test |
《城市达峰指导手册》指出, 城市二氧化碳达峰并不仅仅指某一年二氧化碳排放达到峰值, 只有城市二氧化碳排放出现持续稳定下降, 才意味着城市实现二氧化碳达峰.根据第3节对中国6个城市的情景设定以及第4节的驱动因素分析, 本节预测了北京、上海、广州、深圳、天津和重庆等6个城市在能源强度变化率强度不同时碳排放达峰情况也会明显不同.不同情景下的二氧化碳排放达峰时间和峰值预测如图 1~图 3.
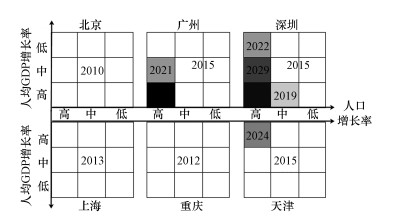 |
| 图 1 高能源强度变化率情景下各城市二氧化碳排放达峰预测 (白色底纹表示到现在已经实现碳达峰, 颜色越深表示碳排放达峰时间越晚, 纯黑色表示在2030年前未实现碳达峰) Fig. 1 Forecast of carbon dioxide emissions peaks in cities under the high energy intensity change rate scenario |
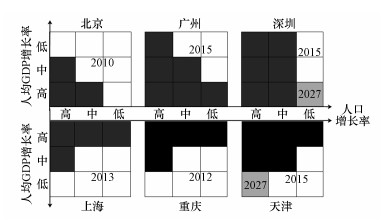 |
| 图 2 能源强度中速率下降下的各城市二氧化碳排放达峰预测 (白色底纹表示到现在已经实现碳达峰, 颜色越深表示碳排放达峰时间越晚, 纯黑色表示在2030年前未实现碳达峰) Fig. 2 Peak prediction of carbon dioxide emissions in cities under the decline of energy intensity |
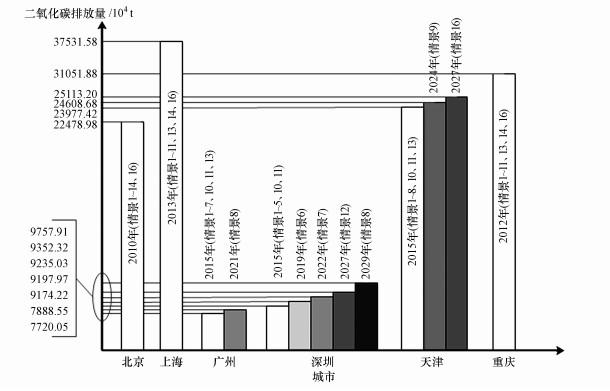 |
| 图 3 北京、上海、广州、深圳、天津和重庆二氧化碳排放峰值及达峰时间 Fig. 3 Peak and peak time of carbon dioxide emissions in Beijing, Shanghai, Guangzhou, Shenzhen, Tianjin and Chongqing |
能源强度以高速率下降下, 北京、重庆和上海均已实现碳排放达峰.北京、重庆和上海的碳排放分别在2010年、2012年和2013年已经达峰, 峰值分别为22478.98×104、31051.88×104和37531.58×104 t.天津碳排放在高能源强度下降情景下均能在2030年前实现达峰:在最宽松的高-高-高情景下会在2024年达峰, 峰值为24608.68×104 t;其余情景下已于2015年达峰, 峰值为23977.42×104 t.除高-高-高情景外, 广州和深圳碳排放在其余情景下均能在2030年前达峰.其中高-中-高情景下的广州碳排放会在2021年达峰, 峰值为7888.55×104 t;其余情景下的广州碳排放在2015年已达峰, 峰值为7720.05×104 t.深圳在高-中-高的情景下的碳排放会在2029年达峰, 峰值为9757.91×104 t;高-低-高情景下的碳排放会在2022年达峰, 峰值为9235.03×104 t;中-高-高情景下的碳排放会在更早的2019年达峰, 峰值为9197.97×104 t;其余情景下的广州碳排放在2015年已达峰, 峰值为9174.22×104 t.
5.1.2 能源强度以中速率下降下的城市碳排放达峰能源强度以中速率下降下, 北京、上海、广州和重庆的碳排放达峰情况基本类似, 深圳和天津的碳排放达峰情况更多样.在能源强度以中速率下降前提下, 北京在低-低/中/高-中、中-低/中-中和高-低-中情景下碳排放已于2010年达峰, 峰值为22478.98×104 t;上海碳排放在低/中/高-低-中和低/中-中-中情景下已于2013年达峰, 峰值为37531.58×104 t;广州碳排放在低-低/中-中和中-低-中情景下已于2015年实现碳排放达峰, 峰值为7720.05×104t;重庆碳排放在低/中/高-低-中和低/中-中-中情景下已于2012年达峰, 峰值为31051.88×104 t;其余情景下的北京、上海、广州和重庆均不能在2030年前实现碳达峰.深圳碳排放在低-低/中-中情景下已于2015年达峰, 峰值为9174.22×104 t;在低-高-中情景下将在2027年达峰, 峰值为9352.32×104 t;其余情景下均未在2030年前达峰.天津碳排放在低-低/中-中和中-低-中情景下已于2015年达峰, 峰值为23977.42×104 t;在高-低-中情景下会在2027年达峰, 峰值为25113.20×104 t;其余情景下均不能在2030年前达峰.
5.1.3 能源强度以低速率下降下的城市碳排放达峰能源强度以低速率下降的前提下, 无论在哪个情景下, 北京、上海、广州、深圳、天津和重庆的碳排放都不能在2030年前实现达峰.因此, 这6个城市要想能够在2030年前达峰, 需要合理制定低碳减排政策, 达到比低能源强度下降率更高的目标.
5.2 各城市碳排放达峰情景及峰值预测北京、上海和重庆的碳排放达峰情况只有1种, 广州、深圳和天津的碳排放达峰情况分别有2种、5种和3种.北京、上海和重庆在高能源强度下降率的全部情景和中能源强度下降率的部分情景下分别已于2010年、2013年和2012年实现碳排放达峰, 而在低能源强度下降率前提的任何情景下都不能实现在2030年前达峰.这意味着北京、上海和重庆的能源强度下降率需要高于低速, 它们才能保证未来的二氧化碳排放量持续降低.广州和深圳在除高-高-高外的高能源强度下降率全部情景和中能源强度下降率的部分情景下均有在2030年前达峰的可能, 但在低能源强度下降率情景下不能实现在2030年前达峰.因为广州和深圳的碳排放量和能源强度本就低于其它四座城市, 低碳减排进程的阻力较大, 所以它们在碳排放方面需要进行全方位管理, 比如加快建设低碳能源体系、着力打造低碳产业体系、健全碳排放权交易机制、加强低碳科技创新、完善低碳基础管理和加强低碳政策落实.天津碳排放在高能源强度下降率的全部情景和中能源强度下降率的部分情景下能够在2030年前实现达峰, 但高-高-高和高-低-中情景下的碳达峰时间从2015年被分别推迟到2024年和2027年, 而在低能源强度下降率前提的任何情景下都不能在2030年前达峰.预测结果表明, 广州、深圳和天津可以根据自身的发展要求来选择合适的碳达峰时间, 制定相应的发展和低碳减排政策.
6 讨论与分析(Discussion and analysis)本文研究6个超大城市, 寻求6个城市碳排放达峰过程中的共性, 研究结果既可以同时对6个城市碳排放达峰提供参考指导, 又能对国内其他城市未来的碳排放管理有前瞻性意义, 而研究方法能对国内其他同类城市的碳排放驱动因素研究有借鉴性意义.通过研究这6个超大城市碳排放特征, 为国内其他城市碳排放研究提供思路, 有效地促进所有城市碳达峰进程, 从而实现全国碳排放达峰目标.从研究方法来看, 本文使用的门限-STIRPAT模型是将STIRPAT模型和门限模型结合起来, 将6城市的面板数据根据能源强度的大小分成合适的几类, 与单一地使用STIRPAT模型研究多城市面板数据相比, 对多个同类城市的碳排放达峰研究有更贴切实际的解释和刻画, 同时验证了能源强度对超大城市碳排放会有阶段性影响.从研究内容来看, 以往使用门限-STIRPAT模型的研究缺少碳排放达峰预测.同时, 以往对城市碳达峰预测时设定的情景较少, 为了能够更全面地预测城市碳排放达峰, 本文设定了27种组合情景.
需要说明的是, 由于数据有限, 本文研究使用的广州和深圳的能源消费统计数据不同于直辖市可以直接得到, 根据广东省的能源消费量间接估计得到, 这可能会对本文研究结果造成一定影响.受到多重共线性等统计问题的影响, 反应碳排放总量相关指标(如能源消费总量、GDP等)无法加入模型当中, 而且对碳排放直接相关的、反应总量相关指标的有限也限制了模型变量的选择.
7 结论(Conclusions)1) 人口、人均GDP和能源强度对城市碳排放的效应均为正, 人口效应最大, 其次是能源强度效应, 人均GDP效应最小.
2) 能源强度对二氧化碳排放的影响呈阶段性变化特征.低于403.43 kg的能源强度水平(万元能耗)对CO2排放的正效应要比能源强度高于404.1960 kg时对CO2排放的正效应小.
3) 6个城市在能源强度变化率强度不同时碳排放达峰的时间也会明显不同.北京、上海和重庆在高能源强度下降率的情景下, 已经达峰;天津、除最宽松的高-高-高情景外的广州和深圳会在2030年前实现达峰.如果能源强度以中速率下降, 6个城市碳排放不能保证一定能在2030年前达峰.如果能源强度以低速率下降, 6个城市均不能在2030年前达峰.
4) 控制人口增长和经济发展的同时, 将重点放在通过技术进步带来的能源强度快速下降是城市碳排放尽快达峰的有效途径.
8 建议(Suggestion)第一, 严格控制人口增速, 能源结构持续优化.能源消费结构优化能有效减少能源消费带来的碳排放量, 并且研究发现人口对城市碳排放的正效应依然是最大的.只要严格控制好人口增速, 提高清洁能源消费比重, 超大城市碳排放目标就能实现.
第二, 注重技术进步, 降低城市的单位GDP能耗.本文研究结果表明高能源强度水平的碳排放正效应要大于低能源强度水平的碳排放正效应.技术的进步, 如引进国内外优秀的技术研究人员、注重清洁能源开发方面的人才培养等, 可以开发出利用效率更高的清洁能源, 在很大程度上降低城市的单位GDP能耗.
第三, 根据各自城市碳达峰目标制定适合本城市的碳达峰政策.由于6个超大城市在不同情景下的达峰情况不同, 相关政府部门可根据本城市设定的达峰目标, 结合情景预测结果, 研究和制定控制碳排放驱动因素变化率的相关政策, 从而完成碳排放达峰目标.
APPC.2017.城市达峰指导手册[OL].2017-04-12, http://www.tanjiaoyi.com/article-21103-1.html
|
邓宣凯, 喻艳华, 刘艳芳. 2014. "十二五"各省区CO2排放控制及减排压力评价[J]. 经济地理, 34(5): 155-161. |
Dong F, Wang Y, Su B, et al. 2019. The process of peak CO2 emissions in developed economies: A perspective of industrialization and urbanization[J]. Resources, Conservation & Recycling, 141: 61-75. |
杜强, 陈乔, 陆宁. 2012. 基于改进IPAT模型的中国未来碳排放预测[J]. 环境科学学报, 32(9): 2294-2302. |
冯宗宪, 王安静. 2016. 中国区域碳峰值测度的思考和研究——基于全国和陕西省数据的分析[J]. 西安交通大学学报(社会科学版), 36(4): 96-104. |
Hansen B E. 1999. Threshold effect in non-dynamic panels: Estimation, testing, and inference[J]. Journal of Econometrics, 93: 345-368. DOI:10.1016/S0304-4076(99)00025-1 |
黄蕊, 王铮. 2013. 基于STIRPAT模型的重庆市能源消费碳排放影响因素研究[J]. 环境科学学报, 33(2): 602-608. |
IPCC.2006. 2006年IPCC国家温室气体清单指南[OL]. 2006-11-23, http://www.ipcc-nggip.iges.or.jp/public/2006gl/chinese/index.html
|
李国志.2011.基于技术进步的中国低碳经济研究[D].南京: 南京航空航天大学 http://cdmd.cnki.com.cn/Article/CDMD-10287-1012033405.htm
|
林伯强, 刘希颖. 2010. 中国城市化阶段的碳排放:影响因素和减排策略[J]. 经济研究, 45(8): 66-78. |
Lin J Y, Kang J F, Khanna N, et al. 2018. Scenario analysis of urban GHG peak and mitigation co-benefits: A case study of Xiamen City, China[J]. Journal of Cleaner Production, 171: 972-983. DOI:10.1016/j.jclepro.2017.10.040 |
刘晴川, 李强, 郑旭煦. 2017. 基于化石能源消耗的重庆市二氧化碳排放峰值预测[J]. 环境科学学报, 37(4): 1582-1593. |
彭智敏, 向念, 夏克郁. 2018. 长江经济带地级城市金融发展与碳排放关系研究[J]. 湖北社会科学, 32(11): 32-38. DOI:10.3969/j.issn.1003-8477.2018.11.006 |
王金南, 蔡博峰, 严刚, 等. 2010. 排放强度承诺下的CO2排放总量控制研究[J]. 中国环境科学, 30(11): 1568-1572. |
王凯, 邵海琴, 周婷婷, 等. 2017. 基于STIRPAT模型的中国旅游业碳排放影响因素分析[J]. 环境科学学报, 37(3): 1185-1192. |
王泳璇.2016.城镇化与碳减排目标背景下能源—碳排放系统建模研究[D].长春: 吉林大学 http://cdmd.cnki.com.cn/Article/CDMD-10183-1016094019.htm
|
Wu C B, Huang G H, Xin B G, et al. 2018. Scenario analysis of carbon emissions′ anti-driving effect on Qingdao′s energy structure adjustment with an optimization model, Part Ⅰ:Carbon emissions peak value prediction[J]. Journal of Cleaner Production, 172: 466-474. DOI:10.1016/j.jclepro.2017.10.216 |
吴立军, 田启波. 2016. 中国碳排放的时间趋势和地区差异研究——基于工业化过程中碳排放演进规律的视角[J]. 山西财经大学学报, 38(1): 25-35. |
吴青龙, 王建明, 郭丕斌. 2018. 开放STIRPAT模型的区域碳排放峰值研究——以能源生产区域山西省为例[J]. 资源科学, 40(5): 1051-1062. |
杨秀, 付琳, 丁丁. 2015. 区域碳排放峰值测算若干问题思考:以北京市为例[J]. 中国人口·资源与环境, 25(10): 39-44. DOI:10.3969/j.issn.1002-2104.2015.10.006 |
叶玉瑶, 苏泳娴, 张虹鸥, 等. 2014. 基于部门结构调整的区域减碳目标情景模拟——以广东省为例[J]. 经济地理, 34(4): 159-165. |
佚名.2010.IPCC收录的各种燃料CO2排放系数[OL].2010-09-30, https://bbs.pinggu.org/thread-871676-1-1.html
|
Yu H, Pan S, Tang B, et al. 2015. Urban energy consumption and CO2 emissions in Beijing: current and future[J]. Energy Efficiency, 8: 527-543. DOI:10.1007/s12053-014-9305-3 |
张乐勤, 陈素平, 王文琴, 等. 2013. 安徽省近15年建设用地变化对碳排放效应测度及趋势预测——基于STIRPAT模型[J]. 环境科学学报, 33(3): 950-958. |
郑海涛, 胡杰, 王文涛. 2016. 中国地级城市碳减排目标实现时间测算[J]. 中国人口·资源与环境, 26(4): 48-54. DOI:10.3969/j.issn.1002-2104.2016.04.007 |
 2019, Vol. 39
2019, Vol. 39


