2. 环境保护部环境规划院, 北京 100012
2. Chinese Academy for Environmental Planning, Ministry of Environmental Protection, Beijing 100012
水环境承载力是指:“一定时期和区域内, 在一定社会经济发展和环境质量保护要求下, 水环境功能可持续发展且不朝恶性方向转变或者发展的条件下, 水环境系统所能支撑的人口、经济、社会可持续发展规模的阈值”(Monte-Luna et al., 2004).对水环境承载力进行评价研究, 可以判断人类活动与水系统功能结构间的协调发展情况, 能为区域社会经济与水环境可持续协调发展的战略规划提供科学依据(曾维华等, 2017).因此, 水环境承载力评价的相关研究对于调节人类自身的社会经济活动, 实现自然-经济-社会的可持续发展具有重要的指导意义和现实意义.
随着环境可持续发展研究的深入, 国内外学者已在水环境承载力评价方面进行了大量探索, 并应用于流域(Wang et al., 2013)、湖泊(Ding et al., 2015)、城市(Venkatesan et al., 2011)和工业(Mao et al., 2012)等各个领域.在水环境承载力评估方面, 常用的方法有灰色关联分析法(Liu, 2013)、多目标优化法(Zhu et al., 2010)、层次分析法(Zhang et al., 2014)、模糊综合评价法(Meng et al., 2009)等.这些评价方法主要通过对评价指标赋权, 以指数形态分辨水环境所处的综合状态, 计算和操作过程相对简单, 可重复性强, 应用较为广泛.在上述较常用的评价方法中, 指标体系的构建和指标权重的确定将直接影响水环境承载力评价结果的可靠性与有效性, 因此, 科学合理地确定指标体系与权重对于水环境承载力的评价研究十分重要.
目前, 在水环境承载力评价体系中, 指标体系的构建往往是遵循科学、合理和适用性的原则, 受主观因素影响较大, 缺乏客观依据(邵强等, 2004).权重的确定方法则主要分为两类(李成等, 2016;刘秋燕等, 2017):一种是由专家根据经验判断各评价指标的相对重要程度, 然后经过综合处理获得指标权重的方法, 如专家调查法、层次分析法等, 这类方法主观性较强, 受人为因素干扰较大.另一种是直接依据各指标数据的特征来确定各评价指标权重的客观方法, 如灰色关联法、熵权法和多元统计法等, 这些方法在一定程度上能够消除主观因素的干扰, 但灰色关联法、熵权法无法反映指标间的相关关系, 不能解决指标间信息重叠的问题;主成分分析法和因子分析法等多元统计法, 通常是假定指标间都是线性关系, 而水环境承载力的指标体系很多情况下是非线性的, 因此, 使用该类方法时也会产生一定的偏差.
结构方程模型(Structural Equation Modeling, SEM)是一种建立、估计和检验因果关系模型的方法.模型中既包含可观测的显在变量, 也可能包含无法直接观测的潜在变量.结构方程模型可以替代多重回归、通径分析、因子分析、协方差分析等方法, 清晰分析单项指标对总体的作用和单项指标间的相互关系, 兼备探索性研究和验证性研究的双重能力, 并具有处理多个因变量、同时估计因子间结构和关系的优点(Jorekog et al., 1993).该模型考虑了误差因素的影响, 弥补了因子分析的缺点, 可以精确估计观察变量和潜在变量之间的关系(刘润润等, 2017), 能够较准确地量化不同指标对水环境承载力的影响关系.因此, 本研究基于SEM结构方程确定水环境承载力评价体系, 并确定权重, 以较好地弥补以往指标体系构建和权重确定方法的不足.
本文以湟水流域小峡桥断面上游为例, 以流域自然汇水边界为主兼顾行政单元, 将研究区划分为16个控制子单元.通过路径分析建立水环境承载力结构方程模型, 并基于结构方程模型潜变量和测变量的选择构建水环境承载力综合评价体系;同时, 基于模型的运行结果, 确定指标权重;进一步应用向量模法对不同控制子单元的水环境承载状态进行综合评价, 从而为湟水流域上下游水系统的持续健康发展提供科学依据.
2 研究方法(Methods) 2.1 研究区概况研究区(图 1)位于青海省东北部, 属高原干旱、半干旱大陆性气候, 多年平均降水量460.5 mm, 地势西北高、东南低.区域内湟水河干、支流呈树枝状水系分布, 药水河、北川河等较大支流在此间汇入, 小峡桥断面是西宁市湟水河干流出境断面.该区域是青海省人口集中、经济发达的集中区域.
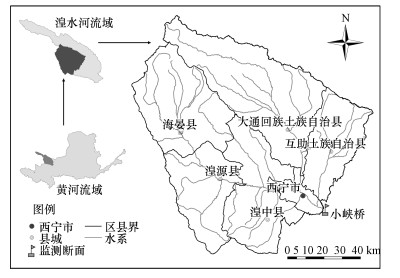 |
| 图 1 研究区地理区位图 Fig. 1 Location of study area |
本研究所涉及的气象、水文数据来源于研究区内各县市的气象站点和水文监测站;水质数据来源于研究区各监测断面的监测数据;污染物排放数据来源于2014年青海省统计年鉴、青海省污染源普查数据、各县市统计年鉴及国民经济社会发展统计资料等.COD和氨氮可用环境容量数据来源于环境保护部环境规划院的研究成果, 其中, COD与氨氮的降解系数借鉴前人研究成果确定(陈龙等, 2016;郭儒等, 2008), COD降解系数为0.25 d-1, 氨氮降解系数为0.2 d-1.土地利用数据为湟水流域小峡桥断面上游水系2014年土地利用数据;遥感影像数据为Landsat TM/OLI遥感影像;进而在ArcGIS软件的支持下, 对各控制单元内土地利用类型的面积进行统计;河流蜿蜒度利用河段长度与河段上下游首尾相连的直线距离之比确定;湿地连通性和聚集度则通过将各个控制单元中的湿地类型转化为栅格数据, 导入到景观格局指数计算软件Fragstats中计算获取.
2.3 结构方程模型的建立结构方程模型凭借优良的多变量分析技巧和处理错综复杂关系的强大能力, 被越来越多的环境领域学者所采用, 并在湖泊及流域水质研究中取得重要进展(颜小品等, 2013), 这为水环境承载力综合评价体系的建立和权重的确定提供了技术支撑.结构方程模型的结构分为测量模型(式(1)~(2))和结构模型(式(3))两部分, 分别是测量方程和结构方程.测量方程以因子分析的方式描述潜变量与测变量之间的关系;结构方程则通过路径关系图来直观地展示潜变量之间的关系.在结构方程模型中, 用潜变量或隐变量表征无法直接测量的现象问题, 用测变量或显变量来表征可直接测量的现象问题(Malaeb et al., 2000;Arhonditsis et al., 2006; ).

|
(1) |
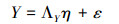
|
(2) |
式中, ξ是外生潜变量;X是ξ的外生测变量;ΛX表示外生测变量与外生潜变量之间的关系;δ是方程残差;η是内生潜变量; Y是η的内生测变量;ΛY表示内生潜变量与内生测变量之间的关系;ε是方程残差.其中, δ与ξ、η及ε之间不存在相关性, ε与η、ξ及δ之间也不存在相关性.

|
(3) |
式中, B表示内生潜变量之间的关系;Γ表示外生潜变量对内生潜变量的影响;ζ是残差项.
2.3.1 结构方程模型路径分析水环境承载状态由水环境承载力和水环境压力共同决定, 容量越大, 压力越小, 则水环境承载力状态越趋于安全, 水环境质量越好.因此, 本研究的指标体系构建从水环境承载力和水环境压力两个角度出发.
① 对于水环境承载力的表征, 主要从产流和水源涵养能力、水质净化能力、上游水质状况3个角度出发.其中, 产流和水源涵养能力即“水量”方面的承载能力, 水质净化能力即“水质”方面的承载能力, 而上游水质状况则强调了水环境的“本底值”大小, 这3个方面较完善地反映了水环境的承载能力.
由大气环流、海陆位置和地形决定的降雨量, 是研究区产流的本底值, 也是影响区域水环境承载力的重要因素.同时, 从土地利用因素对水环境承载力的影响机理方面, 考虑到林地和草地具有蓄含降雨、水源涵养并影响区域产流的能力, 因此, 选择林地面积占比、草地面积占比、水面面积占比和年均降水量表征产流和水源涵养能力.考虑到湿地具有拦截污染物的水质净化能力(郗敏等, 2006), 连通性和聚集度分别是景观对生态流的便利程度及相互分散性的表征(孙贤斌等, 2010;吴际通等, 2014);而蜿蜒度高的河流, 其所具有的植物、微生物资源更为丰富, 有助于提高河流的自净能力(徐彩彩等, 2014).因此, 选择湿地面积占比、湿地连通性、湿地聚集度和河流蜿蜒度表征水质净化能力.
② 从水环境压力上来说, 社会经济活动会给水系统带来巨大压力, 表现为水资源需求与污染物排放.对于水环境压力大小的表征, 本研究从点源污染负荷和面源污染负荷两个角度出发.点源污染主要有工业废水的直接排放, 以及部分城市生活服务等用水直接排放进入水体;面源污染则主要包括农村生产用地中耕地化肥、农药过量使用造成的污染、牲畜养殖等污染及城市不透水面由于降雨径流所形成的污染等.其中, 建设用地和耕地是面源污染过程中主要的土地利用类型(聂发辉, 2008;周婷等, 2009);此外, 农业生产过程中施用化肥(主要是N、P元素的流失)是面源排放量增加的主要因素(钱晓雍等, 2011).因此, 选择不透水面面积占比、耕地面积占比和化肥施用量来表征面源负荷.
综上所述, 考虑到数据的可获得性及土地利用对水环境承载力和压力的影响机理, 确定如图 2所示的影响路径, 以反映不同影响因素与水环境承载状态的关系.
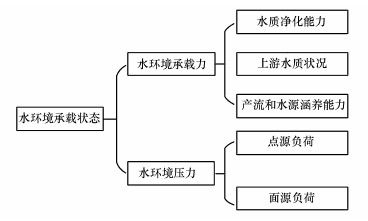 |
| 图 2 结构方程模型构架图 Fig. 2 The structure of structural equation modeling |
从图 2可以看出, 模型架构中的主体变量都不能通过直接测量而得到, 需要用其他指标来具体反映, 这些不可直接测量的变量即为潜变量, 而用以表征潜变量的可直接测量的指标即为测变量.基于科学性、系统性、可靠性和可操作性的原则, 同时考虑到数据的可收集性, 各潜变量对应的表征测变量如表 1所示.
| 表 1 结构方程模型中潜变量与测变量的选择 Table 1 The latent variables and measured variables of the structural equation model (SEM) |
为了获取更多的数据样本量, 在全国控制单元、青海省“十三五”水环境控制单元划分的基础上, 根据湟水河流域地形、水文、水功能区、排污口等实际情况, 以自然水系汇水范围作为陆域划分基准, 将研究区细化为16个控制子单元, 详见图 3.
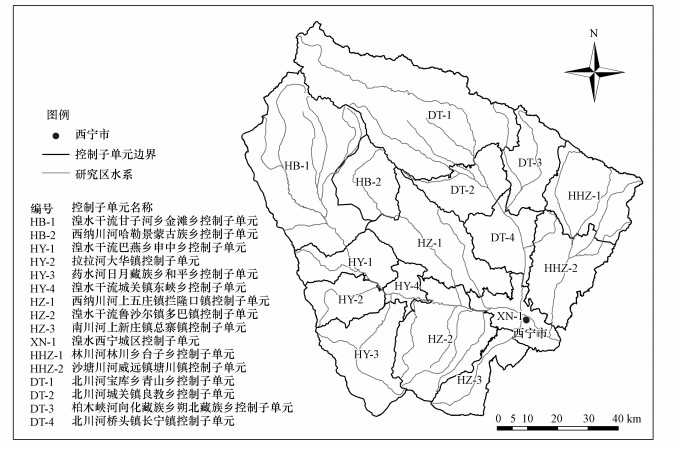 |
| 图 3 控制子单元划分结果 Fig. 3 Divided result of subunits |
在土地利用/景观格局和污染物排放量对水环境承载状态影响路径分析的基础上, 建立面向水环境承载力评价的结构方程模型, 并采用收集的土地利用、水文、水质、气象和污染物排放量数据构成待建结构方程的样本数据组.将原始数据标准化后, 形成SPSS数据格式, 导入AMOS软件中, 运用极大似然法估计(Arhonditsis et al., 2006)进行结构方程模型的量化计算, 以确定模型结构及标准化系数.
2.4 水环境承载力综合评价 2.4.1 综合评价指标体系的构建基于SEM结构方程的路径分析及潜变量和测变量的选择, 构建如表 2所示的水环境承载力综合评价指标体系.
| 表 2 水环境承载力综合评价指标体系 Table 2 An index system for comprehensive evaluation of the water environmental carrying capacity (WECC) |
基于SEM结构方程的计算结果, 确定各变量之间的相关作用系数, 进而计算各层指标的权重, 计算公式如下所示:
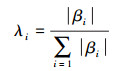
|
(4) |
式中, λi是不同指标相对于总目标的权重, βi是SEM结构方程不同指标层中潜变量与潜变量或测变量与潜变量间的直接相关作用系数.
2.4.3 数据标准化为了消除指标体系中各个指标间量纲的差异, 本文采用极差法对原始数据进行标准化处理, 处理方法如下所示(李磊等, 2014):
发展类指标:
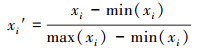
|
(5) |
限制类指标:
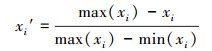
|
(6) |
式中, xi为原始数据;xi′为标准化后的数据;max(xi)和min(xi)分别为原始数据的最大值和最小值.年均降雨量、水面面积占比、河流蜿蜒度等承载力指标为发展类指标;耕地面积占比、化肥施用量、点源负荷排放量等压力指标为限制类指标.发展类指标即正向指标, 其数值越大, 表明水环境承载力越强;限制类指标即负向指标, 数值越小, 表明水环境承载力越强.
2.4.4 计算综合评价指数按照层次分析的思路, 计算出各个指标的权重λi后, 采用“模加和”法求得水环境承载力的综合指数, 计算方法见公式(7)(李美荣等, 2012).
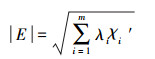
|
(7) |
式中, |E|为水环境承载状态综合指数;λi为第i个元素相对于总目标的权重;xi′为第i个指标标准化后的指标数值.
3 结果与讨论(Results and discussion) 3.1 结构方程模型运行结果分析结构模型能够识别外生潜变量之间可能存在的相关关系及外生变量与内生变量之间的因果关系, 路径系数的大小反映了不同潜变量与水环境质量的相关性(吴明隆, 2010;武文杰等, 2010).经过运行, 结构方程模型的计算结果如图 4所示.为验证模型的有效性, 本文选取常用的绝对指数、相对指数和简约指数对结构方程模型的拟合度进行验证(吴明隆, 2010).模型的绝对指数X2/df和RMSEA的拟合值分别为2.94和0.07, 分别小于标准值3和0.08;GFI的拟合值为0.93, 大于标准值0.9;相对指数NFI和CFI的模拟值分别为0.91和0.93, 均大于标准值0.9;此外, 简约指数PNFI和PCFI的拟合值分别为0.52和0.51, 均大于标准值0.5;各项拟合指数均在拟合标准范围内, 因此, 模型的拟合程度较好, 模型预测可信, 整个测量模型能够较好地解释各个潜变量, 潜变量的总体效度和信度符合要求.
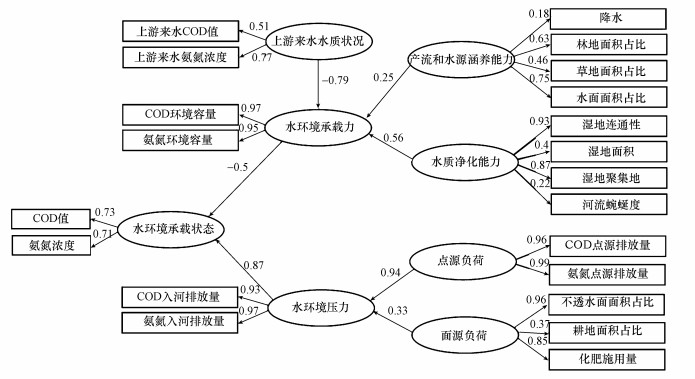 |
| 图 4 结构方程模型的计算结果(矩形框代表测变量, 椭圆框代表潜变量, 单箭头上的数字代表路径系数, +/-表示正相关/负相关) Fig. 4 The calculation results of structural equation modeling |
结果表明, 在湟水流域小峡桥断面上游流域, 水环境承载力和水环境压力与水环境承载状态的相关系数分别为-0.50和0.87, 说明以COD环境容量和氨氮环境容量所表征的承载力与以COD和氨氮浓度所表征的水环境承载状态呈负相关关系, 即水环境承载力越高, 污染物浓度越低, 水质状况越好;以COD入河排放量和氨氮入河排放量所表征的压力与以COD和氨氮浓度所表征的水环境承载状态呈显著正相关关系, 即水环境承载力压力越大, 污染物浓度越高, 水质状况越差.
水环境承载力与上游来水水质显著负相关, 相关系数为-0.79;水环境承载力与水质净化能力显著正相关, 相关系数为0.56;而水资源供给能力与水环境承载力的相关系数仅为0.25.其中, 林地面积占比与水面面积占比与水资源供给能力显著正相关, 相关系数分别为0.63和0.75;湿地连通性和湿地聚集度与水环境水质净化能力显著正相关, 相关系数分别为0.93和0.87.点源负荷与水环境压力显著正相关, 相关系数为0.94;而面源负荷与水环境压力的相关系数仅为0.33;其中, 不透水面面积和化肥施用量与面源负荷显著正相关, 相关系数分别为0.96和0.85.
3.2 权重的计算结果分析基于结构方程模型的计算结果, 利用公式(4)确定各指标权重, 结果见表 3.从表中可以看出, 对水环境承载状态来说, 水环境承载力和压力负荷的权重分别为0.37和0.67, 压力负荷对水环境承载状态的权重远大于水环境承载力, 说明人类活动带来的压力负荷是影响湟水流域小峡桥断面上游水环境质量的主要因素, 其对水环境质量的影响程度大于水环境承载力.对于水环境承载力而言, 上游来水水质对水环境承载力的影响最大, 权重为0.49;水质净化能力次之, 权重为0.35;最后是水资源供给能力, 权重为0.16;这体现了上游水质对水环境承载力影响的重要性, 也从另一方面反映了流域分区精细化管理的重要性.而对于压力负荷而言, 点源负荷和面源负荷对压力负荷的权重分别为0.74和0.26, 点源负荷权重几乎是面源负荷权重的3倍, 说明点源负荷依然是影响湟水流域水环境承载状态的最主要因素之一.
| 表 3 各指标对应权重 Table 3 The weights of each indicators |
对于水资源供给能力来说, 水面面积占比和林地面积占比的权重较大, 分别为0.37和0.31;草地面积占比的权重次之, 为0.23;降水的权重最小, 仅为0.09;说明研究区的林地面积占比、草地面积占比和水面面积占比是提高该区域水资源供给能力的有效指标.湿地连通性和湿地聚集度对水环境承载力的影响较大, 权重分别为0.38和0.36, 其次为湿地面积占比和河流蜿蜒度, 权重分别为0.17和0.09, 说明湿地的连通性和湿地聚集度能够显著的增加研究区的水质净化能力, 因此, 对于湟水流域, 不仅要关注湿地的面积占比, 更要关注湿地的聚集度和连通性.COD点源排放量和氨氮点源排放量对点源负荷的影响相差不大;不透水面面积百分比和化肥施用量是影响面源负荷的重要因素, 权重分别为0.44和0.39;耕地面积百分比次之, 权重仅为0.17.
3.3 水环境承载力综合评价结果及建议根据权重的计算结果, 利用“模加和”法分别计算湟水流域16个控制子单元的水环境承载状态的综合评价指数, 并按照数据从大到小依次划分为好、较好、一般、较差和差5个级别, 具体结果见图 5.从图中可以看出, 湟水流域水环境承载状态呈现出明显的梯度特征, 计算结果与湟水流域的实际情况较为吻合.其中, HB-1、HB-2和DT-1 3个控制子单元均位于研究区主要河流的上游, 水质河段大多为源头水保护区, 隶属于中国易危及地方重点保护鱼类栖息地, 拥有较高的水质本底值;此外, 该区域人口、经济规模最小, 由人为因素造成的压力负荷最小, 故3个控制单元的水环境承载状态最好.建议该部分区域以水源涵养功能和河流廊道生态功能修复为重点, 加强草甸湿地和珍惜濒临危鱼类栖息地保护, 禁止或限制开发, 以保持水环境的承载状态一直处于不超载状态.
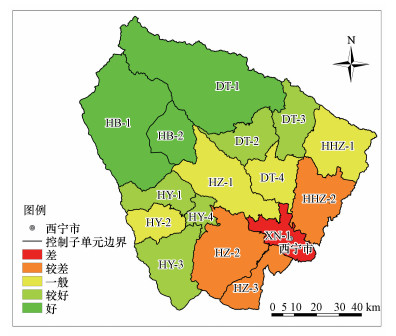 |
| 图 5 水环境承载状态分布图 Fig. 5 The distribution map of the water environmental carrying states |
DT-2、DT-3、HY-1和HY-2 4个控制子单元均位于研究区河流的中上游, 水质的本底值较好, 拥有相对较高的水质净化能力和水资源供给能力, 也属于人口、经济规模较不发达的区域, 农业、工业及生活产生的压力负荷较小, 故也具有相对较好的水环境承载状态.考虑到湟水的海晏至西宁河段为我国濒危、地方重点保护、特有鱼类栖息地, 建议该区以鱼类栖息地规模、功能保护和河流廊道联通性及水流连续性修复为主, 以保障下泄生态流量, 以维持较好的水环境承载状态.
HY-2、HZ-1、HHZ-1和DT-4的水环境承载状态为一般.其中, HY-2、HZ-1和HHZ-1控制子单元内的拉拉河、西纳川河和林川河河段均属于源头和水源地水质, 为高功能水体, 水环境脆弱度高, 拥有较低的实际水环境容量, 且点源和面源负荷处于研究区中等偏下水平, 故呈现出一般的水环境承载状态;北川河中游所在的DT-4控制子单元则处于社会经济较发达区域, 工、农业需水量大且排污较多, 具有较高的压力负荷, 但该区域具有较高的水资源丰裕度, 且高功能水体相对较少, 水系统脆弱度较小, 拥有较大的水环境承载能力, 故该控制单元的水环境承载状态仍为一般.建议该区域以河流基本生态功能维持为重点, 协调开发与保护的关系, 改善水环境质量.
HZ-2、HZ-3、HHZ-2和XN-1主要位于研究区河流的中下游, 均属于人口密集、工业集聚的经济发达区域, 主要的水系包括湟水干流、南川河和北川河等.其中, 湟水干流入河污染物相对集中, 与干流纳污能力分布不匹配, 局部河段入河污染物严重超过其水域的纳污能力;位于XN-1控制子单元的湟水干流、南川河和北川河等西宁城市河段以25%左右的纳污能力承载了全流域约80%的污染负荷, 巨大的压力负荷使湟水西宁河段及其下河段水环境承载状态严重超载.此外, 近年来, 湟水水电站建设密集, 这造成了河流连通性和河道景观破坏, 使河流廊道生态功能严重退化, 进而严重减小了该区的水环境承载能力.因此, HZ-2、HZ-3、HHZ-2和XN-1 4个控制子单元水环境承载状况较差, 且以社会经济最发达、地处湟水流域干流的XN-1控制子单元水环境承载状况最差.建议该区以减排为重点, 通过实施工业点源、农业面源和城市面源综合治理工程及河道生态修复治理专项行动, 减少污染物的入河量, 以降低压力负荷;同时, 在维持生态功能的前提下, 优化土地利用和景观格局, 提高河流自净功能和水源涵养能力, 规范人为开发活动, 禁止不合理开发和开垦.
4 结论(Conclusions)1) SEM结构方程模型能够定量反映土地利用/景观格局及污染物排放因素与水环境承载状态的相关关系.计算结果显示, 以点源负荷和面源负荷表征的水环境压力与水环境承载状态呈显著的负相关关系, 而上游来水水质、水资源供给能力和水质净化能力与水环境承载状态呈显著的正相关关系.其中, 林地面积占比、草地面积占比是影响研究区水资源供给能力的关键因子;湿地连通性和湿地聚集度是影响研究区水质净化能力的主要因素;而面源污染的主要影响因素是耕地面积占比和化肥施用量.
2) SEM结构方程模型的路径分析可为水环境承载力综合评价指标体系的建立提供依据, 其模型运行结果的相关系数能够为权重的确定提供新的方法.研究表明, 压力负荷对水环境承载状态的权重远大于水环境承载力, 且点源负荷权重是面源负荷权重的3倍, 说明尽管我国近年来对环保污染治理进行了一系列的人力、物力、财力投入, 但位处西北地区的湟水流域小峡桥断面上游区域, 在污染治理方面仍处于较低水平, 点源负荷依然是影响湟水流域水环境承载状态的最主要因素之一, 仍需加强该地区域的点源污染控制力度.
3) 水环境承载状态综合评价结果显示, 湟水流域16个控制子单元的水环境承载状态具有明显的梯度特征, 总体来说, 研究区上游区域水环境承载状态较好, 中游区域水环境承载状态一般, 而下游区域水环境承载能力较差.因此, 应针对不同区域的社会、经济、环境和资源差异, 进行分区化精细管理, 因地制宜的制定水污染防治与水资源利用的政策措施.
4) 人口规模扩大和工业快速增长所导致的需水量增加, 以及大量污水排放和农业面源污染是导致湟水流域小峡桥断面上游水体污染的主要原因.因此, 从提高水环境承载力和减小水环境压力的双向调控角度出发, 加强湟水流域水资源管理, 是改善湟水流域水环境质量, 确保流域内经济社会可持续发展, 实现生态环境良性循环的必要途径.
Arhonditsis G B, Stow C A, Steinberg L J, et al. 2006. Exploring ecological patterns with structural equation modeling and Bayesian analysis[J]. Ecological Modeling, 192: 385–409.
DOI:10.1016/j.ecolmodel.2005.07.028
|
陈龙, 曾维华. 2016. 渭河干流关中段非突发性水质超标风险研究[J]. 人民黄河, 2016, 38(2): 80–83.
DOI:10.3969/j.issn.1000-1379.2016.02.021 |
Ding L, Chen K L, Cheng S G, et al. 2015. Water ecological carrying capacity of urban lakes in the context of rapid urbanization:A case study of East Lake in Wuhan[J]. Physics & Chemistry of the Earth Parts A/b/c, s 89-90: 104–113.
|
郭儒, 李宇斌, 富国. 2008. 河流中污染物衰减系数影响因素分析[J]. 气象与环境学报, 2008, 24(1): 56–59.
DOI:10.3969/j.issn.1673-503X.2008.01.014 |
Jorekog K G, Sorbom D.1993.New features in PRELIS 2[R].Chicago: Scientific Software
|
Liu H. 2013. The impact of human behavior on ecological threshold:Positive or negative?-Grey relational analysis of ecological footprint, energy consumption and environmental protection[J]. Energy Policy, 56(5): 711–719.
|
李美荣, 郑钦玉, 刘娟, 等. 2012. 基于AHP法的重庆市水环境承载力研究[J]. 水利科技与经济, 2012, 18(5): 1–6.
DOI:10.3969/j.issn.1006-7175.2012.05.001 |
李磊, 贾磊, 赵晓雪, 等. 2014. 层次分析-熵值定权法在城市水环境承载力评价中的应用[J]. 长江流域资源与环境, 2014, 23(4): 456–460.
DOI:10.11870/cjlyzyyhj201404002 |
李成, 吴谦, 胡满. 2016. 风险综合评价中指标权重确定方法对比研究[J]. 石油工业技术监督, 2016, 32(1): 50–53.
DOI:10.3969/j.issn.1004-1346.2016.01.014 |
刘润润, 薛景丽, 郑新奇. 2012. 结构方程模型在城市研究中的应用述评[J]. 资源开发与市场, 2012, 28(3): 222–226.
DOI:10.3969/j.issn.1005-8141.2012.03.010 |
刘秋艳, 吴新年. 2017. 多要素评价中指标权重的确定方法评述[J]. 知识管理论坛, 2017(6): 500–510.
|
Malaeb Z A, Summers J K, Pugesek B H. 2000. Using structural equation modeling to investigate relationships among ecological variables[J]. Environmental and Ecological Statistics, 7(1): 93–111.
DOI:10.1023/A:1009662930292
|
Meng L, Chen Y, Weihong L I, et al. 2009. Fuzzy comprehensive evaluation model for water resources carrying capacity in Tarim River Basin, Xinjiang, China[J]. Chinese Geographical Science, 19(1): 89–95.
DOI:10.1007/s11769-009-0089-x
|
Mao I F, Chen M R, Wang L, et al. 2012. Method development for determining the malodor source and pollution in industrial park[J]. Science of the Total Environment, 437(20): 270–275.
|
Monte-Luna P D, Brook B W, Zetina-Rejón M J, et al. 2004. The carrying capacity of ecosystems[J]. Global Ecology & Biogeography, 13(6): 485–495.
|
钱晓雍, 沈根祥, 郭春霞, 等. 2011. 基于水环境功能区划的农业面源污染源解析及其空间异质性[J]. 农业工程学报, 2011, 27(2): 103–108.
|
聂发辉.2008.上海城市景观绿地削减地表径流及其污染负荷的可行性研究[D].上海: 同济大学
http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1450957 |
邵强, 李友俊, 田庆旺. 2004. 综合评价指标体系构建方法[J]. 东北石油大学学报, 2004, 28(3): 74–76.
DOI:10.3969/j.issn.2095-4107.2004.03.025 |
孙贤斌, 刘红玉. 2010. 土地利用变化对湿地景观连通性的影响及连通性优化效应——以江苏盐城海滨湿地为例[J]. 自然资源学报, 2010, 25(6): 892–903.
|
Venkatesan A K, Ahmad S, Johnson W, et al. 2011. Systems dynamic model to forecast salinity load to the Colorado River due to urbanization within the Las Vegas Valley[J]. Science of the Total Environment, 409(13): 2616–2625.
DOI:10.1016/j.scitotenv.2011.03.018
|
Wang S, Yang F L, Xu L, et al. 2013. Multi-scale analysis of the water resources carrying capacity of the Liaohe Basin based on ecological footprints[J]. Journal of Cleaner Production, 53(16): 158–166.
|
吴际通, 顾卿先, 喻理飞, 等. 2014. 贵州草海湿地景观格局变化分析[J]. 西南大学学报(自然科学版), 2014, 36(2): 28–35.
|
吴明隆. 2010. 结构方程模型:AMS的操作与应用[M]. 重庆: 重庆大学出版社.
|
武文杰, 刘志林, 张文忠. 2010. 基于结构方程模型的北京居住用地价格影响因素评价[J]. 地理学报, 2010, 65(6): 676–684.
|
郗敏, 刘红玉, 吕宪国. 2006. 流域湿地水质净化功能研究进展[J]. 水科学进展, 2006, 17(4): 566–573.
DOI:10.3321/j.issn:1001-6791.2006.04.022 |
徐彩彩, 张远, 张殷波, 等. 2014. 辽河流域河段蜿蜒度特征分析[J]. 生态科学, 2014, 33(3): 495–501.
|
颜小品, 李玉照, 刘永, 等. 2013. 基于结构方程的农村水环境管理评价研究基于结构方程模型的滇池叶绿素a与关键影响因子关系识别[J]. 北京大学学报(自然科学版), 2013, 49(6): 1031–1039.
|
曾维华, 薛英岚, 贾紫牧. 2017. 水环境承载力评价技术方法体系建设与实证研究[J]. 环境保护, 2017(24): 17–24.
|
Zhu Y, Drake S, Lü H, et al. 2010. Analysis of temporal and spatial differences in eco-environmental carrying capacity related to water in the Haihe River Basins, China[J]. Water Resources Management, 24(6): 1089–1105.
DOI:10.1007/s11269-009-9487-1
|
Zhang Z, Lu W X, Zhao Y, et al. 2014. Development tendency analysis and evaluation of the water ecological carrying capacity in the Siping area of Jilin Province in China based on system dynamics and analytic hierarchy process[J]. Ecological Modelling, 275: 9–21.
DOI:10.1016/j.ecolmodel.2013.11.031
|
周婷, 彭少麟, 任文韬. 2009. 东江河岸缓冲带景观格局变化对水体恢复的影响[J]. 生态学报, 2009, 29(1): 231–239.
DOI:10.3321/j.issn:1000-0933.2009.01.029 |
 2019, Vol. 39
2019, Vol. 39


