大气气溶胶具有影响全球气候和环境的效应, 近年来已成为科学家们广泛研究的一个重要领域(Lohmann et al., 2002; Menon et al., 2002; Nishizawa et al., 2002; Penner et al., 2004).大气气溶胶中的PM2.5(fine particulate matter, 空气动力学直径小于2.5 μm的固体颗粒物), 因其对人类健康(殷永文等, 2011; 杨维等, 2013; 谢元博等, 2014)和大气能见度产生严重的负面影响, 已受到各国政府及研究部门的高度重视(邵龙义等, 2000; 徐建辉等, 2015).自改革开放以来, 京津冀地区一直是中国的政治、经济、文化中心, 同时, 京津冀地区也是全国水资源最短缺, 大气污染、水污染最严重, 资源环境与发展矛盾最为尖锐的地区(杜艳春等, 2017), 其人口密度大、工业集群规模大、能耗大, 使得京津冀地区成为我国空气污染最重的区域, PM2.5污染已成为当地人民群众的“心肺之患”, 是京津冀地区首要污染物(Liang et al., 2007).国家发改委、原环保部发布的《京津冀协同发展生态环境保护规划》明确提出到2020年PM2.5浓度比2013年下降40%左右.获得高精度、全覆盖的PM2.5时空分布状况, 是制定减缓PM2.5区域联动有效措施的前提和基础.
传统PM2.5的监测方法有滤膜称重法、光散射法(朱一川等, 2003)和微量振荡天平法(张予燕等, 2006), 虽然这些方法可以得到具体某地的较高精度的监测结果, 但是对于监测点以外的广大区域无法进行监测并且监测成本高昂, 形成监测盲区, 不利于大范围的PM2.5时空分布监测.霾的形成主要是以人类活动排放到大气环境中的地面颗粒物为主, 大气颗粒物浓度与气溶胶光学厚度密切相关, 目前基于气溶胶光学厚度与气象数据构建AOD-PM2.5估算模型在国内外已成为研究热点, 现有研究构建的模型主要有比例因子法、基于物理机理的半经验公式法和统计模型法3种方法(Ma et al., 2016).基于卫星遥感AOD数据反演地面PM2.5浓度的比例因子法, 优点是不需要监测站点数据也能获知其PM2.5污染状况, 但也只是针对长期的平均浓度, 对于日、月和季节等短期的估算精度不太理想(Liang et al., 2007; Lang et al., 2017; Chen et al., 2018); 基于物理机理的半经验公式法反演效果要略优于比例因子法, 但其公式中的一些参数不易获取, 限制了该方法的推广; 统计模型法相较于比例因子法和半经验公式法, 估算精度更高、灵活性更强, 因此得到了广泛应用, 不足之处是需要大量实测数据进行模型构建和结果验证(Ma et al., 2016).估算结果的空间分辨率与精度的提高是目前大气遥感学者致力于解决的科学问题之一.NASA发布的AOD产品有3种, 分别为空间分辨率1°的3级产品、10 km和3 km的2级产品、1 km的1级产品.气象数据目前可获取到的为0.25°×0.3125°的气象网格数据与中国气象数据共享服务网(http://data.cma.cn/)提供的气象观测站点数据.气象观测站点的数据在插值处理时误差具有不可控制性, 以此方法构建的模型, 估算效果不理想.而网格气象数据由于分辨率较粗, 在研究中小尺度环境问题时, 其空间分辨率难以满足模型要求, 目前的处理方法是将气象网格数据重采样为10 km或3 km, 但重采样过程中的误差将直接影响估算结果, 抑制模型精度的提高.
地理加权回归模型(Geographically Weighted Regression, GWR)由于其可以解释地理预测因子的空间变异性和非平稳性(Rob et al, 2013; 汉瑞英等, 2016), 逐渐被应用于污染物浓度空间分布预测研究中, 并取得了较好的效果.汉瑞英等(2016)利用GWR模型模拟了杭州市PM2.5质量浓度的空间分布.卢亚灵等(2014)利用GWR模拟了2010年中国地级城市SO2年均质量浓度.Zhang等(2016)利用GWR模型和增强型植被指数模拟了中国大陆PM2.5质量浓度的空间分布.空间降尺度方法目前被广泛用来解决降水、地表温度和土壤湿度等遥感产品空间分辨率不足的问题.本文为解决AOD-PM2.5模型构建过程中的数据空间分辨率不匹配问题, 构建模型时, 在地理加权回归模型的基础上引入了空间降尺度方法.本文采用GWR空间降尺度方法, 以京津冀地区为案例区, 以月为单位估算了2017年京津冀地区的PM2.5时空分布, 经验证, 精度较高, 不但解决了模型构建过程中的空间分辨率不匹配的问题, 而且提高了模型估算的精度.
2 数据与方法(Data and methods) 2.1 遥感数据来源与预处理 2.1.1 MODIS AOD数据AOD数据来源于NASA搭载在Aqua卫星上的MODIS传感器上的遥感影像产品, Optical_Depth_Land_And_Ocean数据集(MODIS/Aqua Aerosol 5-Min L2 Swath 3 km V006)数据获取自https://ladsweb.modaps.eosdis.nasa.gov/search/order网站.该数据具有多光谱、宽覆盖和时间分辨率高等特点, 被广泛用于大气气溶胶监测.产品空间分辨率为3 km, 波长为550 nm, 采用暗像元算法反演.通过ENVI/IDL语言编程和HDF4函数库对数据集进行批量重投影、镶嵌、裁剪等处理.采用平均值合成法, 从日产品最终得到月尺度的AOD数据.篇幅所限, 图 1仅显示了研究区2017年1月份的AOD空间分布图.
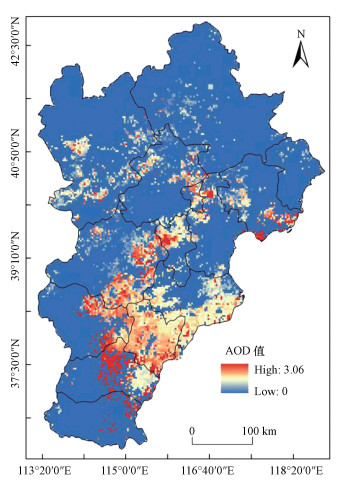 |
| 图 1 京津冀地区2017年1月的AOD空间分布 Fig. 1 The spatial distribution of AOD in January 2017 |
气象数据来源于第5版的戈尔德地球观测系统的网格化气象数据产品(http://rain.ucis.dal.ca/ctm/), 该气象数据产品也是GEOS-Chem全球CTM模型的气象输入数据.采用IDL语言批量提取该网格数据与Aqua/MODIS卫星过境时刻的气象数据, 包括大气边界层高度(PBLH)和平均相对湿度(RH), 其空间分辨率为0.25°(纬度)×0.3125°(经度).Koelemeijer等(2006)和Guan等(2014)发现对AOD进行垂直和湿度订正可以显著提高PM2.5估算精度, 马宗伟等(2015)和张世乔等(2017)在构建模型时加入了风速、降水和气压等气象数据构建模型, 但精度提高有限.本文尝试在减少数据量的同时构建更优的AOD-PM2.5模型.图 2为京津冀区域PBLH(a)和RH(b)空间分布图.
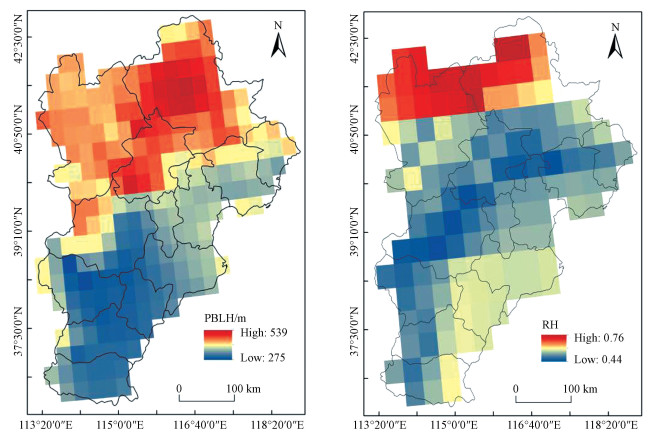 |
| 图 2 京津冀区域PBLH(a)和RH(b)空间分布 Fig. 2 Spatial distribution of PBLH(a) and RH(b) in Beijing-Tianjin-Hebei region |
PM2.5质量浓度数据来源于国家生态环境部(http://www.zhb.gov.cn/)公布的实时空气质量报告, 统计时间为2017年1月1日—2017年12月31日.选取研究区内及其周边地区共130个环境监测站点进行模型构建, 此外, 采用随机抽样法选取了研究区内16个环境监测站点(不含在模型构建的130个站点内)的数据进行模型验证, 并对个别缺测数据进行剔除处理.图 3为获取的环境监测站点的样本点(a)和验证点(b)空间分布示意图.
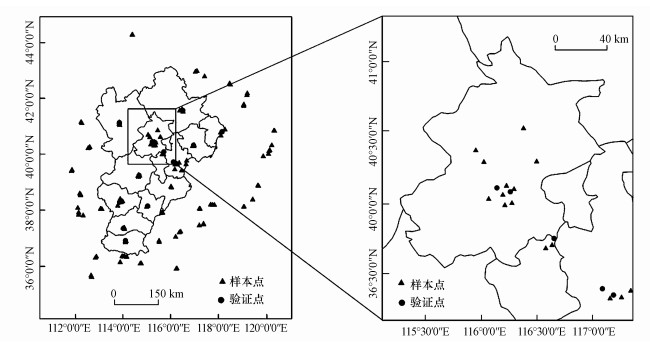 |
| 图 3 样本点(a)和验证点(b)空间分布示意图 Fig. 3 Spatial distribution of sample points(a) and verifying points(b) |
GWR是一种空间分析技术, 被广泛应用于地理学及涉及空间模式分析的相关学科.GWR通过建立空间范围内每个点处的局部回归方程, 来探索研究对象在某一尺度下的空间变化及相关驱动因素(胡艳兴等, 2015).由于它考虑到了空间对象的局部效应, 更具优势.因此, 以GWR为基础来构建AOD-PM2.5模型, 并引进空间降尺度思想对该模型进行改进, 得到可估算PM2.5的地理加权回归空间降尺度模型.在GWR模型建模时选取高斯函数作为核函数, 生成连续变化的权重矩阵, 核函数类型设置为调整型(Adaptive), 相较于固定型(Fixed)更为灵活, 适应于站点分布不均的京津冀地区, 并采用交叉验证(Cross Validation)的方法确定最优带宽(Ma et al., 2016).篇幅所限, GWR的计算公式详见参考文献(胡艳兴等, 2015).
2.2.2 空间降尺度空间降尺度是将大尺度、低分辨率的信息转化为小尺度、高分辨率信息的一种方法, 降尺度的提出是建立在美国国家气象局天气预报的全球气候模式基础上, 由于该气候模型在预估未来全球气候变化时, 存在输出的空间分辨率较低(通常为300 km)、缺少详细的区域气候信息等缺点(尤加俊等, 2015), 因此, 学者们提出了降尺度方法, 该方法很好地解决了这一问题, 并广泛应用于气候研究领域.近年来, 降尺度方法被广泛用来解决降水、地表温度和土壤湿度等遥感数据的空间分辨率不足问题(嵇涛等; 2015等; 李净等, 2015; 尤加俊等, 2015), 但在污染物遥感估算和空间分布方面的研究案例尚不多见.PM2.5估算的模型构建中, 输入的栅格数据空间分辨率不同, 图 1为空间分辨率3 km的AOD数据, 图 2a和图 2b分别为空间分辨率为0.25°的PBLH和RH数据, 因分辨率低, 在与图 1相同的比例下已能看到格网.前人(Guo et al., 2013; Ma et al., 2016)在用遥感数据估算PM2.5时, 多以重采样法统一数据的空间分辨率, 将PBLH和RH重采样至3 km, 这种方法对原数据造成了破坏, 影响了模型反演的精度.为解决这一问题, 本文在构建AOD-PM2.5模型时引入空间降尺度方法, 大大提高了估算的精度.地理加权回归空间降尺度模型的构建过程如下:
将两种不同空间分辨率的遥感数据分为相对的高分辨率数据(HR)和低分辨率数据(LR), 其中HR包括空间分辨率3 km的大气气溶胶产品(AODHR), 双线性内插重采样后的3 km的大气边界层高度(PBLHHR)和相对湿度(RHHR)数据.LR包括空间分辨率0.25°×0.3125°的大气边界层高度(PBLHLR)和相对湿度(RHLR), 以及最邻近内插重采样后的低空间分辨率气溶胶光学厚度(AODLR)数据.利用公式(1)对监测站点k处的数据进行模型训练, 以求得该研究区内各模型输入数据的系数, 再对已知系数和相应的栅格数据进行求解.AOD、PBLH、RH与PM2.5之间在月均尺度上存在如下的最优关系:
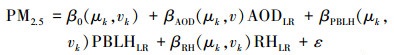
|
(1) |
式中, PM2.5代表环境监测站点的实测值, (μk, Vk)用来表示地面环境监测站点k的空间坐标, AODLR、PBLHLR、RHLR分别代表k处的模型输入参量, β0、βAOD、βPBLH和βRH分别是各模型输入数据需要求解的系数, ε是随机误差.
由k处低空间分辨率为0.25°的AODLR、PBLHLR、RHLR数据和求解出的各数据对应的系数β0、βAOD、βPBLH和βRH, 计算得到月均PM2.5的预测值PLR.
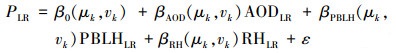
|
(2) |
式中, PLR代表低空间分辨率的PM2.5月均预测值(μg·m-3), AODLR是由空间分辨率3 km的AOD重采样至0.25°的低空间分辨率数据, 其它符号代表含义同式(1).
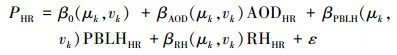
|
(3) |
式中, PHR代表高空间分辨率的PM2.5预测值, PBLHHR和RHHR是由低空间分辨率0.25°的PBLHLR和RHLR采用双线性内插法重采样至3 km的高空间分辨率的数据.
再计算得到0.25°分辨率下预测值(PLR)与PM2.5实测数据之间的月均尺度的残差(ΔPM2.5LR):
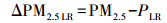
|
(4) |
对0.25°栅格中心点残差值插值得到高分辨率的月均尺度的残差值(ΔPM2.5HR), 空间分辨率为3 km, 这里采用常用的反距离权重IDW插值、样条函数插值、自然邻近插值3种插值方法.
最后, 将高空间分辨率的残差(ΔPM2.5HR)和预测的高空间分辨率PM2.5值相加, 得到最终该模型预测的3 km × 3 km栅格的PM2.5月均质量浓度PPM2.5:
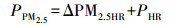
|
(5) |
本文选取研究区及周边地区的130个空气监测站点数据和大气遥感气溶胶数据构建其与PM2.5的回归模型(式(1)), 得到逐月的最优系数.依据最优系数估算低分辨率的PM2.5空间分布(式(2)), 并进一步提取与站点相对应的PM2.5估算值, 将其与站点实测值做差值(式(4)), 得到低分辨率的PM2.5残差, 对低分辨率的残差选取3种最常用的插值方法进行插值, 分别为反距离加权插值、样条插值和最邻近插值, 再分别加上高分辨率的PM2.5预测值, 最终得到降尺度后的PM2.5质量浓度及其空间分布.技术路线如图 4所示.
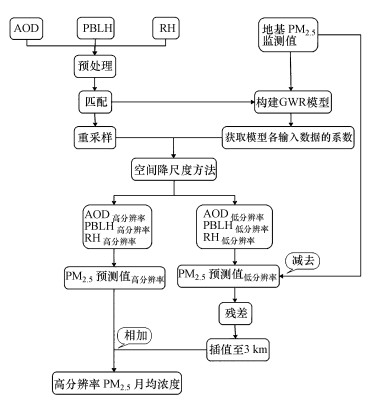 |
| 图 4 GWR空间降尺度技术路线 Fig. 4 Technical flow chart of GWR spatial downscaling |
为全面客观地评价本文构建的GWR空间降尺度方法的估算精度, 采用预测值和地面观测值之间的决定系数(R2)、平均预测误差(Mean Prediction Error, MPE)、均方根预测误差(Root Mean Squared Prediction Error, RMSE)、相对预测误差(Relative Prediction Error, RPE)等指标评价该模型.具体含义和计算方法如下:
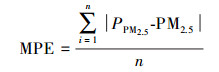
|
(6) |
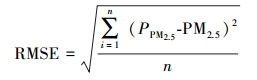
|
(7) |
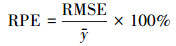
|
(8) |
式中, n为建模数据集记录总数; y为建模样本集的PM2.5浓度均值, 其它符号含义同上.
2.3 稳定性分析采用变异系数来计算2017年1—12月逐月每个栅格PM2.5的稳定性, 从而揭示PM2.5的年内变化特征.变异系数是一种量度数据分布的分散程度之标准, 用其来评估PM2.5在时间序列上的稳定性(叶辉等, 2012), 计算式为:
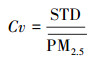
|
(9) |
式中, Cv为变异系数, STD为标准偏差, 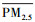
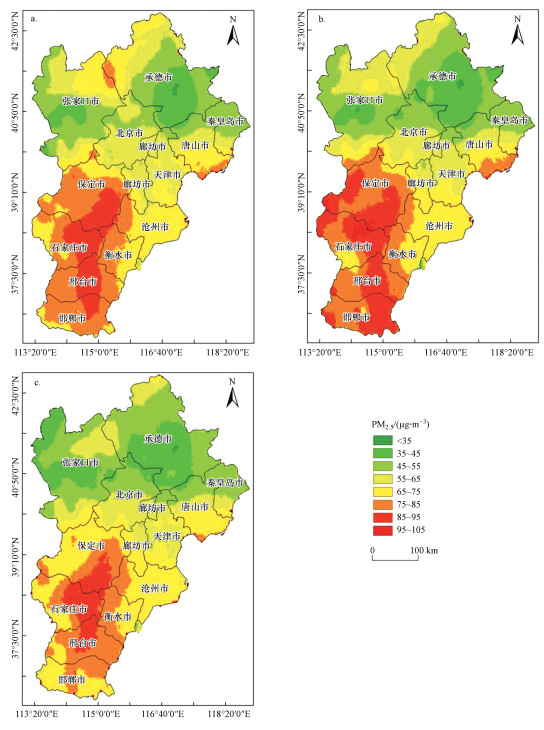
GWR降尺度方法对残差值的处理方法共选取了3种不同的方法, 基于3种不同残差插值方法修正后的PM2.5浓度空间分布如图 5所示.图 5是由2017年1—12月估算的月尺度PM2.5质量浓度求均值得到的PM2.5质量浓度年平均空间分布.图 5a为基于IDW残差插值修正后的估算结果, 图 5b为基于薄盘样条函数残差插值修正后的估算结果, 图 5c为基于自然邻近法残差插值修正后的估算结果.从图 5可以看出, 不同残差插值方法下的地理加权回归模型空间降尺度方法估算的PM2.5结果大体上保持一致, 只在京津冀南部和北部地区的分布略有差异.其中, 图 5a的模拟结果显示, 在北部有不显著的IDW插值后的圆环状痕迹; 图 5b的模拟结果空间上在南部区域的PM2.5高值区相比于其他两种残差插值修正后的PM2.5高值区域范围更大, 浓度更高; 图 5c的模拟结果则显示, 空间上在南部区域的PM2.5质量浓度高值区集中分布在中部, 其两翼浓度较低.
 |
| 图 5 不同残差插值方法修正后的2017年均PM2.5遥感估算空间分布 Fig. 5 Estimation of spatial distribution of modified PM2.5 using different residual interpolation methods |
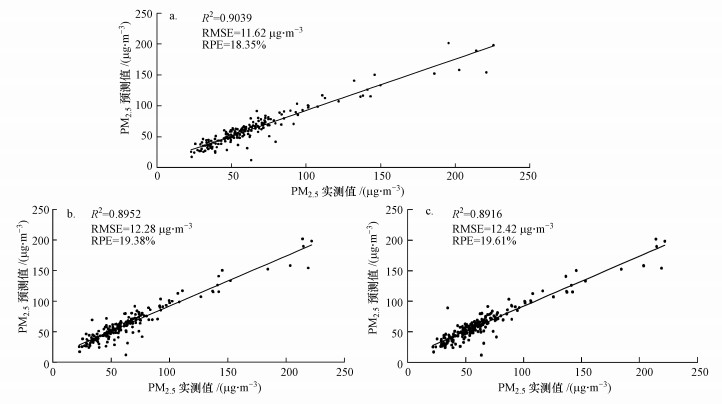
本次研究将146个环境监测站点分为相互独立的样本点和验证点两部分.在京津冀及周边地区130个空气质量监测站点作为样本点来进行AOD-PM2.5模型的构建, 以及遥感数据拟合系数的训练.为精确评价估算结果的精度, 选取验证站点时考虑了站点的代表性与空间分布的均匀性, 在研究区内共选取了均匀分布的16个站点作为验证数据.利用预留的16个地面空气监测站点逐月监测数据, 经剔除个别缺测站点数据后, 2017年共获得185组有效数据.通过对模型预测的PM2.5值和地基环境监测站点的PM2.5进行匹配, 计算出r、R2、MPE、RMSE和RPE, 以便对比基于3种不同残差插值的地理加权回归空间降尺度方法的建模效果.图 6a、图 6b、图 6c分别为基于自然邻近残差修正后、基于IDW残差修正后和基于薄盘样条函数修正后的模型估算的PM2.5值与地基监测站点的PM2.5值的拟合散点图.图 6显示, 模型估算的PM2.5预测值和地面观测值有极强的一致性, 估算精度很高, 通过了95%的置信水平检验, 基于IDW、薄盘样条函数和自然邻近3种不同残差插值方法下的调整后R2分别为0.895、0.8916和0.903.
 |
| 图 6 3种不同残差插值修正后模型预测和地面监测的PM2.5质量浓度相关性散点图 Fig. 6 Scatter plots of PM2.5 mass concentration correlation for model prediction and ground monitoring after interpolation with different residuals |
经对比3种残差处理模型后发现, 在GWR空间降尺度过程中对残差的处理, 选取自然邻近残差修正后的模拟效果最优(图 6a), 通过95%的置信水平下, 其r=0.951, R2=0.904, 调整后R2=0.903, MPE=7.307 μg·m-3, RMSE=11.62 μg·m-3, RPE=18.35%, 说明该模型能客观估算京津冀地区2017年PM2.5质量浓度.其次是基于反距离加权残差插值的GWR空间降尺度方法(图 6b), 通过95%的置信水平下, r=0.946, R2=0.895, 调整后R2=0.895, MPE=7.79 μg·m-3, RMSE=12.28 μg·m-3, RPE=19.38%;最后是基于薄盘样条函数残差插值修正后的GWR空间降尺度方法(图 6c), 通过95%的置信水平下, r=0.944, R2=0.892, 调整后R2=0.891, MPE=7.91 μg·m-3, RMSE=12.42 μg·m-3, RPE=19.61%.
为评估该模型估算的PM2.5质量浓度结果, 用京津冀地区空气质量监测站点与估算结果进行比对(用来验证的12个月份共185个验证数据), 对比分析结果如图 7所示, 从图 7中可看到, 各时间节点上, 遥感预测值与地面监测结果保持较高的一致性.然而, 由于AOD原数据产品在1月份的缺失值较多, 对模型模拟精度造成了干扰, 加之1月份为全年PM2.5质量浓度的最高月, 使得出现了高值被高估的现象, 这一现象也是AOD-PM2.5模型估算中最容易出现的问题之一(贾松林等, 2014; 李荣等, 2015).
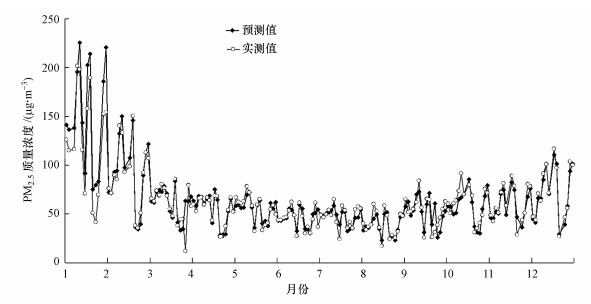 |
| 图 7 遥感估算与地面观测PM2.5质量浓度对比 Fig. 7 Comparison of PM2.5 mass concentration between remote sensing with ground observation |
将本文估算的结果与国内相关学者采用其它模型模拟PM2.5空间分布的精度验证结果进行比较(表 1), 也发现本文模拟的精度较高, 说明利用GWR降尺度方法可以很好地模拟京津冀地区PM2.5的空间分布格局.
| 表 1 中国学者代表性的PM2.5-AOD统计模型和验证结果 Table 1 Typical PM2.5-AOD statistical model and verification results of Chinese scholars |
经过对模型的训练和精度验证, 发现本文改良后的GWR空间降尺度方法具有3方面优势:①该模型考虑了地理位置在空间上的变化, 可以消除空间变异的影响, 在尺度上相较于众多AOD-PM2.5模型中具有更强的适用性; ②基于前人高级统计模型的基础, 加入空间降尺度思想, 解决了模型输入的不同数据源的数据空间分辨率不匹配问题; ③通过残差插值修正估算的结果, 显著提高了模型估算的精度.
3.3 PM2.5空间分布 3.3.1 总体分布格局经验证, 基于自然邻近残差插值修正后的PM2.5模拟结果最优.从图 5c可知, 2017年均PM2.5呈现出南高北低的空间分布特征.PM2.5质量浓度呈现非常显著的“纬度地带性”:PM2.5质量浓度低(<55 μg·m-3)的区域几乎全部分布在40°N以北的区域, 包括承德市、张家口市、秦皇岛市, 以及唐山市和北京市的北部区域.PM2.5质量浓度很高(<80 μg·m-3)的区域则全部集中在39°N以南的地区, 尤其以保定市南部、石家庄市东部和邢台市大部区域最高.较高污染区主要分布在唐山市南部、保定市北部、廊坊市西南部、天津市南部、沧州市大部、衡水市东部、邯郸市西部和东南部、石家庄市西部等区域.PM2.5南部高值区又可分为中部极高污染区与两翼较高污染区.京津冀地区南北PM2.5污染格局形成的主要原因是由于不同的自然地理环境与人文社会经济环境差异所致, 该区域北部的地形单元以山地丘陵为主, 人口密度小, 经济支柱产业为旅游业, 污染物排放较少且位于冬季风的上风向, 在冬季风作用下, 有利于大气污染物的稀释扩散, 因而大气环境质量优良.相反, 冀中南地区在京津产业转型时承接了其大部分的耗能产业, 在拉动经济发展的同时也造成了大气环境的污染.值得注意的是, PM2.5质量浓度南北高低值区域界线与市级行政界线具有一定的一致性.
3.3.2 稳定性分析大气移动性较强, 稳定程度较为复杂, 变异系数可基于像元准确地表征PM2.5的稳定性程度.由图 8可知, PM2.5在2017年内的稳定程度与PM2.5质量浓度空间分布具有反向性, 即PM2.5质量浓度高的区域稳定性弱, 年内的波动程度剧烈, 而PM2.5质量浓度低的区域稳定性高, 年内变化程度微弱.稳定性弱的区域主要分布在河北的保定、石家庄等工业区域, 该区域受产业类型影响, 大气污染物排放能力强; 人口众多, 社会经济活动活跃, 对大气环境的胁迫性强; 在风速、湿度等天气因素的影响下变化幅度较大, 因此PM2.5稳定性弱, 对人类健康的影响具有强危险性和难预测性.这说明PM2.5浓度高的区域也恰好是最不稳定的区域.京津冀地区北部的区域以第一产业为主, 大气污染物排放较少, 加之人口稀少, 对大气环境的胁迫性较弱, 因此PM2.5稳定性强.
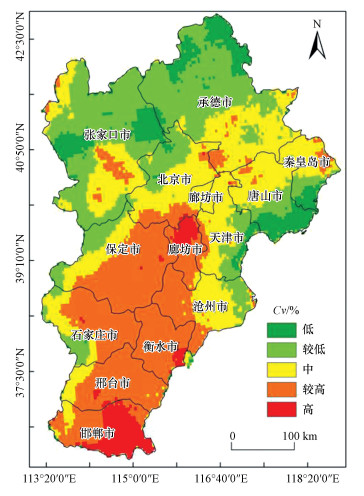 |
| 图 8 PM2.5空气质量稳定程度 Fig. 8 Air quality stability of PM2.5 |
PM2.5的直接来源可分为自然源和人为源(张文等, 2016).2017年京津冀地区年均PM2.5空间分布呈现出南高北低, 南繁北简的态势.PM2.5质量浓度的南北高低值区域界线与保定市和沧州市的市级界线具有较高的一致性, 保定市和沧州市以南的区域为PM2.5高值区, 以北为PM2.5的低值区, PM2.5南部高值区又可分为中部高污染区与两翼较高污染区.京津冀地区南北PM2.5污染差异形成的主要原因是由于不同的自然地理环境与人文环境, 该区域北部的地形单元以山地丘陵为主、人口密度小、经济支柱产业为旅游业, 污染物排放较少且位于冬季风的上风向, 在冬季风作用下, 有利于大气污染物的稀释扩散, 因而大气环境质量优良.2017年均PM2.5南部高值区形成的原因主要以人类活动为主, 该区域毗邻京津, 在京津产业转型时承接了其大部分的耗能产业, 在拉动经济发展的同时也造成了大气环境的污染.目前, 京津冀地区PM2.5浓度高, 导致霾大量产生的原因, 一是直接燃煤产生的原始结构的PM2.5, 二是再生性PM2.5, 即由氮氧化物、硫化物、挥发性有机物等物质在一定的湿度和光的作用下产生的亚硫酸盐、硫酸盐、亚硝酸盐、硝酸盐等颗粒性物质, 加之京津等大城市周边汽车保有量较大, 汽车排放的挥发性有机物等物质的增加致使再生性PM2.5增多.减排措施上, 针对不同规模的直接燃煤采用不同的方式实施改造, 车用燃料采用无氧燃料转变为含氧燃料、电并存发展, 城市居民生活采用管道燃气和电并存, 农村居民生产生活采用电和醇并存, 工业、商业、餐饮业、企事业等用能单位采用电、燃气和醇并存发展.PM2.5质量浓度南北高低值区域界线与市级行政界线具有一致性的实际则提示, 区域差别化的能源结构和产业结构的选择及调整, 将直接影响PM2.5浓度和空气质量优劣.
目前, PM2.5的遥感估算多以10 km的AOD产品为基础, 建立AOD-PM2.5模型, 用空间分辨率更高的3 km的AOD产品为基础构建AOD-PM2.5模型的研究极少, 这是因为3 km的AOD数据处理起来相较于10 km的AOD数据更困难.10 km分辨率的AOD数据有暗目标算法、深蓝算法和暗目标-深蓝融合算法3种产品, 像元缺失较少, 而3 km的AOD数据只有暗像元一种算法, 在高亮地表像元缺失较多, 在一定程度上会影响PM2.5的估算.气象格网数据的空间分辨率为0.25°, 前人基于10 km的AOD建模过程中采用了重采样的方式进行处理, 但是对于3 km的AOD建模, 对于PBLH和RH格网数据进行重采样必然是不可行的, 因此, 在建模中解决不同的数据空间分辨率不匹配这一问题, 显得迫在眉睫.被估算的10 km的PM2.5其空间分辨率难以满足小尺度研究, 本研究估算的3 km的PM2.5在中小尺度上更具有优势.
影响区域PM2.5质量浓度的因素众多, 本文只选取了PBLH和RH, 是基于以下考虑.①前人(Guo et al., 2014)研究发现PBLH和RH的订正可以提高夏季PM2.5与AOD的相关关系.②用尽量少的模型输入数据, 提高估算精度, 减少工作量, 凸显GWR降尺度方法的优势.通过将本研究的结果和精度与前人研究结果相对比, 本文模拟的京津冀地区的PM2.5质量浓度与吴健生等(2017)的结果相近, 对同一区域的研究, 本研究提出的模型能更好地模拟PM2.5空气质量浓度, 相关系数R2提高了20%, 误差控制(RMSE和RPE)降低了约10%.不同学者研究结果有所不同, 主要原因:①研究的时间序列不同; ②数据产品不同; ③数据源空间分辨率不同.后续研究可以尝试使用WRF模拟的大气相对湿度、风速、边界层高度等气象因子, 对气溶胶光学厚度AOD分别进行订正, 以提高AOD与近地面PM2.5间的相关性, 并优选反演模型研究PM2.5的空间分布特征.
5 结论(Conclusion)基于MODIS 3 km气溶胶产品、GEOS-5 FP 0.25°×0.3125°的气象网格数据和PM2.5地基实测数据, 提出了GWR空间降尺度方法, 并估算了2017年1—12月京津冀地区的PM2.5月均质量浓度, 且分析了京津冀地区月尺度上的PM2.5稳定性.结果表明本研究构建的GWR降尺度方法较好地解决了AOD-PM2.5模型构建过程中众多输入数据空间分辨率不匹配的问题.基于GWR空间降尺度方法中残差的处理, IDW、样条函数和自然邻近3种残差修正后的方法均具有理想的效果.经验证, GWR降尺度方法提高了PM2.5估算的精度, 具有较显著的优势.对于降尺度过程中残差的插值处理, 共选取大气数据常用的3种插值方法, 经交叉验证, 结果显示基于反距离残差插值后的模型精度R2=0.895, 样条残差插值后的模型精度R2=0.891, 邻近残差插值后的模型精度R2=0.903, 因此, 基于自然邻近残差插值的GWR降尺度方法为最优.
致谢: 王晓磊为本研究收集和整理了PM2.5环境监测站点数据, 特此致谢.
Chen G, Li S, Knibbs L D, et al. 2018. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information[J]. Science of the Total Environment, 636: 52–60.
DOI:10.1016/j.scitotenv.2018.04.251
|
陈辉, 厉青, 张玉环, 等. 2016. 基于地理加权模型的我国冬季PM2.5遥感估算方法研究[J]. 环境科学学报, 2016, 36(6): 2142–2151.
|
杜艳春, 葛察忠, 何理, 等. 2017. 京津冀传统产业绿色转型升级的瓶颈与政策建议[J]. 中国人口资源与环境, 2017(S2): 107–110.
|
Guan D, Su X, Zhang Q, et al. 2014. The socioeconomic drivers of China's primary PM2.5 emissions[J]. Environmental Research Letters, 9(2): 024010.
DOI:10.1088/1748-9326/9/2/024010
|
郭建平, 吴业荣, 张小曳, 等. 2013. BP网络框架下MODIS气溶胶光学厚度产品估算中国东部PM2.5[J]. 环境科学, 2013, 34(3): 817–825.
|
Guo Y, Feng N, Christopher S A, et al. 2014. Satellite remote sensing of fine particulate matter (PM2.5) air quality over Beijing using MODIS[J]. International Journal of Remote Sensing, 35(17): 6522–6544.
DOI:10.1080/01431161.2014.958245
|
汉瑞英, 陈健, 王彬. 2016. 利用LUR模型模拟杭州市PM2.5质量浓度空间分布[J]. 环境科学学报, 2016, 36(9): 3379–3385.
|
郝静, 孙成, 郭兴宇, 等. 2018. 京津冀内陆平原区PM2.5浓度时空变化定量模拟[J]. 环境科学, 2018, 39(4): 1455–1464.
|
胡艳兴, 潘竟虎, 王怡睿. 2015. 基于ESDA-GWR的1997-2012年中国省域能源消费碳排放时空演变特征[J]. 环境科学学报, 2015, 35(6): 1896–1906.
|
黄旭, 郭云霞, 刘剑斌, 等. 2017. 柳州大气PM2.5中糖类物质的分布特征与指示意义[J]. 中国环境科学, 2017, 37(3): 838–843.
|
嵇涛, 刘睿, 杨华, 等. 2015. 多源遥感数据的降水空间降尺度研究——以川渝地区为例[J]. 地球信息科学学报, 2015, 17(1): 108–117.
|
贾松林, 苏林, 陶金花, 等. 2014. 卫星遥感监测近地表细颗粒物多元回归方法研究[J]. 中国环境科学, 2014, 34(3): 565–573.
|
Koelemeijer R, Homan C, Matthijsen J. 2006. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe[J]. Atmospheric Environment, 40(27): 5304–5315.
DOI:10.1016/j.atmosenv.2006.04.044
|
Lang J, Zhang Y, Zhou Y, et al. 2017. Trends of PM2.5 and chemical composition in Beijing, 2000-2015[J]. Aerosol & Air Quality Research, 17(2): 412–425.
|
李净, 张晓. 2015. TRMM降水数据的空间降尺度方法研究[J]. 地理科学, 2015, 35(9): 1164–1169.
|
李荣. 2015.中国典型地区PM2.5时空分布估算建模方法与应用研究[D].北京: 中国科学院大学
|
Liang F, Xiao Q, Wang Y, et al. 2017. MAIAC-based long-term spatiotemporal trends of PM2.5 in Beijing, China[J]. Science of the Total Environment, 616-617: 1589–1598.
|
Liang F, Meng G, Xiao Q, et al. 2017. Evaluation of a data fusion approach to estimate daily PM2.5 levels in North China[J]. Environmental Research, 158: 54–60.
DOI:10.1016/j.envres.2017.06.001
|
Lohmann U, Lesins G. 2002. Stronger Constraints on the Anthropogenic Indirect Aerosol Effect[J]. Science, 298(5595): 1012–1015.
DOI:10.1126/science.1075405
|
卢亚灵, 蒋洪强, 黄季夏, 等. 2014. 基于GWR的中国地级城市SO2年均质量浓度模拟[J]. 生态环境学报, 2014, 23(8): 1305–1310.
DOI:10.3969/j.issn.1674-5906.2014.08.009 |
马宗伟. 2015.基于卫星遥感的我国PM2.5时空分布研究[D].南京: 南京大学
|
Ma Z W, Hu X F, Sayer A M, et al. 2016. Satellite-based spatiotemporal trends in PM2.5 concentrations:China, 2004-2013[J]. Environ Health Perspect, 124(2): 184–192.
DOI:10.1289/ehp.1409481
|
Menon S, Hansen J, Nazarenko L, et al. 2002. Climate effects of black carbon aerosols in China and India[J]. Science, 297(5590): 2250–2253.
DOI:10.1126/science.1075159
|
Nishizawa T, Asano S, Uchiyama A, et al. 2004. Seasonal variation of aerosol direct radiative forcing and optical properties estimated from ground-based solar radiation measurements[J]. Journal of the Atmospheric Sciences, 61(1): 57–72.
|
Penner J E, Dong X, Chen Y. 2004. Observational evidence of a change in radiative forcing due to the indirect aerosol effect[J]. Nature, 427(6971): 231–234.
DOI:10.1038/nature02234
|
Rob B, Gerard H, Danielle V, et al. 2013. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe-The ESCAPE project[J]. Atmospheric Environment, 72(2): 10–23.
|
邵龙义, 时宗波, 黄勤. 2000. 都市大气环境中可吸入颗粒物的研究[J]. 环境保护, 2000(1): 24–26.
|
吴健生, 王茜, 李嘉诚, 等. 2017. PM2.5浓度空间分异模拟模型对比:以京津冀地区为例[J]. 环境科学, 2017, 38(6): 2191–2201.
|
谢元博, 陈娟, 李巍. 2014. 雾霾重污染期间北京居民对高浓度PM2.5持续暴露的健康风险及其损害价值评估[J]. 环境科学, 2014, 35(1): 1–8.
|
徐建辉, 江洪. 2015. 长江三角洲PM2.5质量浓度遥感估算与时空分布特征[J]. 环境科学, 2015, 36(9): 3119–3127.
|
杨维, 赵文吉, 宫兆宁, 等. 2013. 北京城区可吸入颗粒物分布与呼吸系统疾病相关分析[J]. 环境科学, 2013, 34(1): 237–243.
|
叶辉, 王军邦, 黄玫, 等. 2012. 青藏高原植被降水利用效率的空间格局及其对降水和气温的响应[J]. 植物生态学报, 2012, 36(12): 1237–1247.
|
殷永文, 程金平, 段玉森, 等. 2011. 上海市霾期间PM2.5、PM10污染与呼吸科、儿呼吸科门诊人数的相关分析[J]. 环境科学, 2011, 32(7): 1894–1898.
|
尤加俊, 安如. 2015. 基于CCI和MODIS数据的淮河流域地表土壤湿度降尺度方法研究[J]. 测绘与空间地理信息, 2015, 38(2): 30–34.
DOI:10.3969/j.issn.1672-5867.2015.02.010 |
张世乔, 江洪, 王祎鑫, 等. 2017. 京津唐地区PM2.5遥感估算与区域传输[J]. 遥感信息, 2017, 32(4): 11–23.
DOI:10.3969/j.issn.1000-3177.2017.04.003 |
Zhang T, Gong W, Wang W, et al. 2016. Ground level PM2.5 estimates over China using satellite-based Geographically Weighted Regression (GWR) models are improved by including NO2, and Enhanced Vegetation Index (EVI)[J]. International Journal of Environmental Research and Public Health, 13(12): E1215.
DOI:10.3390/ijerph13121215
|
张文, 潘竟虎. 2016. 2013年大范围雾霾期间京津冀PM2.5质量浓度遥感估算及时空变化的经验正交函数分析[J]. 兰州大学学报(自然科学版), 2016, 52(3): 350–356.
|
张予燕. 2006. β射线法与振荡天平法测定环境中PM10的对比分析[J]. 仪器仪表与分析监测, 2006(1): 45–46.
DOI:10.3969/j.issn.1002-3720.2006.01.020 |
朱一川, 张晶, 周文刚, 等. 2003. LD-3C型微电脑激光粉尘仪及其质量浓度转换系数K值的测定[J]. 中国环境卫生, 2003(1): 103–107.
|
 2019, Vol. 39
2019, Vol. 39


