2. 杭州市环境保护科学研究院, 杭州 310014
2. Hangzhou Institute of Environment Sciences, Hangzhou 310014
近年来, 随着城市化进程的快速发展和机动车保有量的急剧增加, 长三角地区环境空气污染特征发生了显著的变化, 特别是在夏季, 臭氧(O3)已逐渐成为空气污染的首要污染物.近地面O3的主要来源之一是氮氧化物(NOx)和挥发性有机物(VOCs)在紫外线作用下产生的二次污染(叶贤满等, 2015; 严仁嫦等, 2018).其中的氮氧化物不仅会产生光化学污染, 而且还会对人体的呼吸系统、神经系统等造成一定的危害, 增加过敏、支气管炎等疾病的发病率(Hsu et al., 2001; Khreis et al., 2017).在城市环境中, NOx主要来源于移动源和工业源排放, 根据杭州本地污染源调查发现(杨强等, 2017), 移动源排放的氮氧化物占总量的69.2%, 其中, 机动车尾气排放占移动源排放的65.9%, 机动车尾气排放已成为城市NOx的重要来源, 对其污染排放的控制是改善城市空气质量的优选目标之一, 而精准预测NOx浓度变化则可以为管控提供相应的数据支撑, 因此, 对NOx浓度进行准确预测非常重要.
针对城市区域空气污染物浓度预测的模型有CALINE4模型(Dhyani et al., 2016)、时间序列模型(陈亚玲等, 2013; 苗蕾等, 2016)、贝叶斯时空模型(朱亚杰等, 2016)等.随着人工智能的发展, 越来越多的学者开始利用智能算法对空气污染物浓度进行预测.王黎明等(2017)利用距离相关系数筛选预报因子, 再利用支持向量机回归方法对PM2.5浓度进行逐日滚动预报, 获得了良好的预测效果, 相关系数达到0.76.孙宝磊等(2016)利用BP人工神经网络对SO2、NO2、CO等6种大气污染物建立了日均浓度预测模型, 将前1 d所有污染物浓度数据和前5 d某种污染物数据作为预报输入, 对某一种污染物浓度进行预报, 获得了较好的预报效果, R2多大于0.6.Grivas等(2006)结合人工神经网络和遗传算法对雅典4个监测站点的PM10小时浓度进行了预测, 发现该模型与多个线性回归模型相比, 预测性能更加优越, R2在0.5~0.67之间, 而线性回归模型的R2仅在0.29~0.35之间.这些预测方法的精度还达不到环保工作精准化管理的要求, 特别是在特殊情况下(如排放严格管控的杭州G20会议期间)预测精度不高, 因此, 需要寻找新方法进一步提升预测精度、拓宽使用范围.
决策树算法常用于分类预测及规则提取, 在医疗分析、灾害预警等领域均有很好的应用(赵建华等, 2006;Tehrany et al., 2013;姜宛贝等, 2016), 受到这些应用研究的启发, 在研究空气环境中NOx浓度预测时, 可探索用决策树算法以进一步提升预测精度、拓宽使用范围.基于此, 本研究以污染物数据、气象数据和交通流量数据为基础, 利用决策树中的CART回归树算法, 以实现NOx(主要考虑NO与NO2之和)浓度的预测, 并建立支持向量机模型和BP神经网络模型与之进行对比, 分析CART回归树预测模型的预测性能, 为NOx浓度预测提供多模型参考.
2 方法(Methods) 2.1 CART回归树决策树算法是从一组无序的实例中推理出自上而下的树状分类规则, 利用树的结构对数据进行分类, 它代表着对象属性与对象值之间的一种映射关系, 树的每个结点代表某个对象, 其中每个分叉路径则代表该对象可能的属性值, 每个叶结点则是对应根结点根据各个属性分类到的对象的值.决策树算法通常包括3个步骤:特征选取、决策树生成和决策树修剪(张秀英等, 2008; 张棪等, 2016).
分类与回归树CART(classification and regression tress)算法是是一种广泛应于分类和回归的决策树算法, 其内部是一种二叉树结构, 在每个节点利用最优划分依据将数据划分至两个不同的子集, 通过不断迭代, 将数据划分至更均匀的子集中, 直至满足停止条件.CART决策树分为分类树与回归树, 分类树通过一个对象的特征来预测该对象所属的类别, 而回归树则是根据对象的信息预测对象的属性, 并以数值表示.本研究结合影响NOx浓度变化的因素与CART回归树的特点, 实现对NOx浓度的预测.
2.2 数据来源及数据预处理 2.2.1 数据来源研究区域地处杭州市延安路中心商业区.研究使用的数据包含两类:路边空气质量监测站(以下简称“路边站”)的环保数据和电子警察抓拍识别数据.其中, 路边站的环保数据涵盖2016年6月1日—9月20日污染物数据(包含PM2.5、PM10、NO2、CO、NO、O3浓度数据)和气象数据(包含风向、风速、温度、湿度), 数据来源为杭州市环境监测中心站, 数据更新频率为1次·min-1;电子警察抓拍识别数据涵盖2016年6月1日—9月20日之间经过该抓拍点位时车辆的相关信息, 包括抓拍时刻、抓拍点位名称、道路编号、车牌、车牌类型等信息, 研究仅利用抓拍时刻与车牌信息计算出该点位的车流量, 数据来源于杭州市交通数据, 数据更新频率为1次·min-1.路边站与抓拍点位位置如图 1所示, 经过该路边站的车流主要有由北向南和由南向北两路车流, 路边站距抓拍点位1约20 m, 距抓拍点位2约500 m, 距体育场路延安路交叉口约170 m.通过抓拍点位1获取由北向南的车流量, 抓拍点位2获取由南向北的车流量.
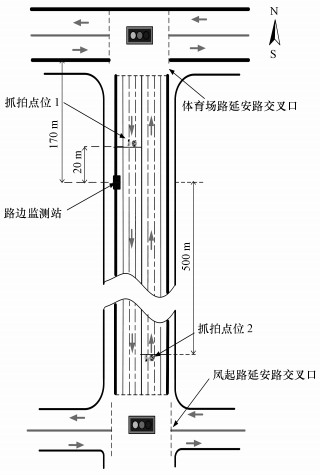 |
| 图 1 数据位置示意图 Fig. 1 Data location diagram |
数据质量对后续算法的预测起着重要的作用, 因而需对数据进行预处理, 以减少对后续算法运行的影响.环保数据异常主要有两种, 其一:突发的外界环境变化导致某些监测设备未能及时响应, 从而产生突发异常数据, 如下雨时, PM10浓度数据偶尔会跳跃至零点, 甚至负数, 此类异常数据持续时间较短, 直接予以剔除.第二种异常数据产生的原因是监测设备的临时维护, 维护时该设备所监测项目将会出现较长时间段的零值, 此类异常数据持续时间较长, 若直接对其予以剔除将对原始数据序列造成较大损坏, 故利用特定算法对此类异常数据进行修复处理.本文采用K最邻近(K-Nearest Neighbor, KNN)算法对此类较长时间的异常数据进行填充修复.图 2展示了部分PM10原始数据, 从图中可以清晰看到原始PM10数据中存在的两种异常情况.
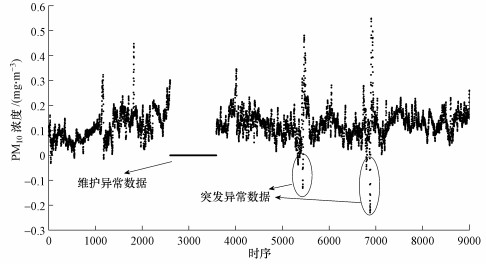 |
| 图 2 PM10部分异常数据 Fig. 2 Partial exception data of PM10 |
KNN算法是基于实例学习的非参数估计方法, KNN算法认为系统内各因素的内在联系均蕴含于历史数据中, 缺失值可通过历史数据库中与估计值的特征向量最相似的K个数据进行加权估计得到(王翔等, 2015).以上述PM10浓度数据因设备维护而产生的数据异常为例进行数据修复, 异常时段的PM10浓度作为需要估计的估计值, 以此时数据样本中其它数据(除PM10以外的其它环保数据)作为特征向量, 在历史数据库中寻找K个与特征向量距离最近的历史特征向量, 从而估计出异常时段的PM10浓度, 其表达式如下:
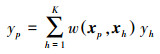
|
(1) |
式中, yp为p时段需要估计的估计值;xp为p时段估计值的特征向量;w(xp, xh)为根据特征向量xp与xh之间的距离所计算得到的权重;yh为搜索到的历史值;K取5.
数据预处理主要步骤描述如下:①剔除小于零的无意义数据;②设定阈值Ts=10 min, 对数据进行遍历, 若数据出现连续为零的时长≤Ts, 则认为该数据是因突发原因导致的, 予以剔除, 反之, 认为该数据是因设备维护导致的, 对这部分数据应用KNN算法进行数据修复;③对抓拍数据进行数据处理, 将抓拍时刻与车牌信息提取后, 进行统计, 得出每分钟经过的车流量;④对处理后的环保数据集和抓拍数据集进行整合, 以时间为基准合并两个数据集.
以图 2所示的部分PM10浓度数据为例, 对其进行数据预处理后结果如图 3所示, 可以看出, 经过数据预处理后, 异常数据已基本处理完成, 数据质量得到明显提升.
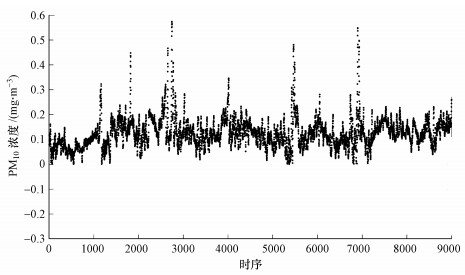 |
| 图 3 预处理后的PM10数据 Fig. 3 Pre-processed data of PM10 |
在城市商业区, 机动车是NOx的主要来源, 车流量的变化将直接影响着NOx浓度的高低.在训练集数据中随机抽取连续7 d(168 h)的车流量数据与NOx浓度数据, 绘制NOx浓度与车流量关系图.如图 4所示, 左侧纵坐标表示NOx浓度值, 右侧纵坐标表示车流量, 实线表示NOx浓度变化, 虚线表示车流量变化.从图中可以发现, 在每日4:00后, 随着城市生活的开始, 车流量迅速增加, 随后NOx浓度随之开始攀升.并且, 车流量在每日8:00左右达到第一个波峰之前, NOx浓度的第一个波峰已经到来.20:00之后, 车流量开始减少, 随后NOx浓度开始降低, 且20:00之后NOx浓度波谷的到来要早于车流量波谷.8:00—20:00, 车流量相对平稳, 而NOx浓度的变化则不尽相同, 因为除了车流量之外, 大气环境中其它因素同样影响着NOx浓度的变化.即车流量与NOx浓度在早晚高峰时, 虽然在时间上不同步, 但仍存在着相似的变化趋势, 故选取车流量作为预测目标NOx浓度的特征之一.
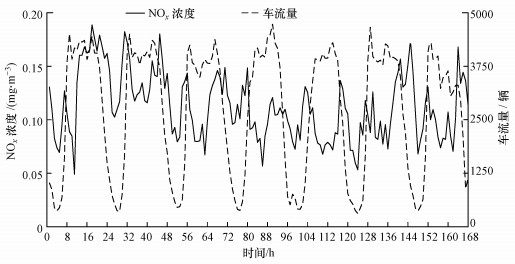 |
| 图 4 NOx浓度与车流量关系图 Fig. 4 The relationship between NOx concentration and vehicle flow |
利用Pearson相关性分析法研究了NOx浓度与风向、风速、温度、湿度之间的相关性, 结果如图 5所示.由图 5a、5b可知, 风向、风速与NOx浓度呈负相关, 且相关系数在气象因素中为较大的两个, 可见风是影响NOx浓度消散的重要因素.从图 5c、5d可以发现, 温度与湿度均对NOx有一定的影响, 温度与NOx浓度呈负相关, 而湿度与NOx浓度则呈现正相关, 这与其他研究结果吻合(宋从波等, 2016; 徐鹏等, 2016).因此, 本文选取这4个气象因素作为预测目标NOx的特征.
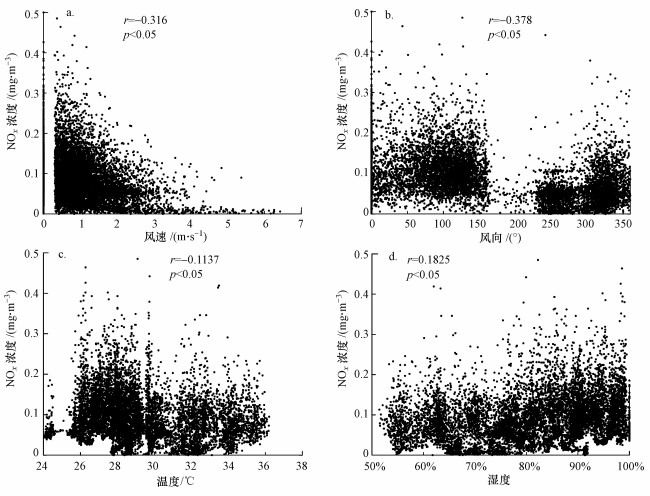 |
| 图 5 NOx浓度与气象因素的散点图(a.风速, b.风向, c.温度, d.湿度) Fig. 5 Scatter plot of NOx concentration and meteorological factors |
其它污染物与NOx浓度也有显著相关性, 图 6为CO、O3、PM2.5、PM10与NOx的Pearson相关性分析结果.由图可知, CO浓度与NOx浓度相关系数最高, 主要是由于研究区域CO和NOx的主要来源都为机动车尾气;O3浓度与NOx浓度呈显著负相关, 这是因为NOx是O3形成的重要前体物之一, 在大气环境中经过一系列的化学反应会转化成O3;PM2.5和PM10浓度与NOx浓度均呈正相关, 但相关系数较小, 这可能与PM2.5和PM10的贡献来源复杂有关, 既来自道路扬尘, 又来自机动车尾气等.
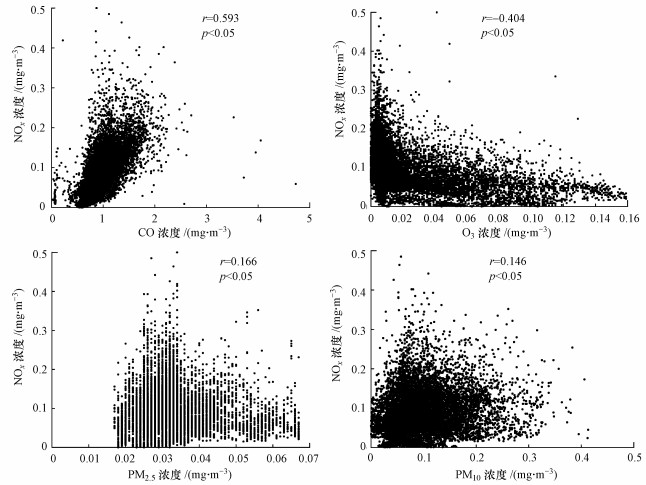 |
| 图 6 NOx浓度与其它污染物的散点图(a.CO, b.O3, c.PM2.5, d. PM10) Fig. 6 Scatter plots of NOx concentrations and other pollutants |
综上, NOx浓度与上述众多因素之间均线性相关, 但相关系数均不大, 这是因为NOx随着机动车尾气排放至大气环境中后, 环境中各因素对氮氧化物的扩散及转化的影响是一个复杂的非线性过程, 利用简单的线性预测手段对NOx浓度进行预测较为困难, 故提出以CART决策树算法为基础的机器学习方法对NOx浓度进行预测.
2.4 CART回归树构建CART回归树构建过程如下:
1) 特征选取:选取前文所述各个影响因素为特征向量.
2) CART回归树的生成:从根结点开始, 将所有训练数据放在根结点, 通过选择最佳特征, 在每个结点上进行布尔判断, 判断为真的划归为左子树, 其余的划归为右子树, 即递归地二分每个特征, 将训练数据集划分为有限个子集.
子集的划分可以描述为:对于输入变量x和输出变量y, 当选择第j个特征向量x(j)和它的取值s作为划分特征和划分点时, 定义两个子集:
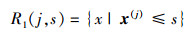
|
(2) |
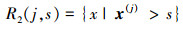
|
(3) |
式中, R1(j, s)表示第以第j个特征向量的取值s划分的左子树, R2(j, s)表示第以第j个特征向量的取值s划分的右子树.最佳划分变量j和最佳划分点s即求:
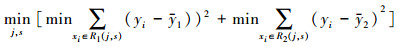
|
(4) |
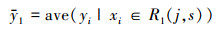
|
(5) |
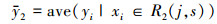
|
(6) |
式中, yi表示输入变量xi对应的输出变量, xi∈R1(j, s)表示在第j个特征向量的取值s划分下, 属于左子树的输入变量.通过遍历所有输入变量, 找到最佳划分变量j和最佳划分点s并构成一对(j, s), 然后依次将集合划分至两个子集.重复上述划分过程, 直至满足停止条件.
3) 回归树的剪枝:为避免生成的回归树出现过拟合现象, 需对树的生长进行一定限制, 以获得模型更好的泛化能力, 采用预剪枝方法, 经过交叉验证后得到, 设置最小划分所需样本数为6, 即某结点的样本数少于6, 则不会再进行划分.
2.5 NOx浓度预测模型选用预报时间车流量、当前时间其它污染物浓度及预报时间气象条件作为模型输入, 以获得预报时间NOx的浓度值(图 7).已有历史数据更新频率为1次·min-1, 但考虑实际应用中无法获得分钟级别的预报数据, 结合杭州市实际情况, 将历史数据进行统一处理, 转化为更新频率为1次/30 min, 以30 min级别的数据作为模型输入(模型输入数据的时间频率不是固定的, 可根据实际情况进行改变).而对于空气污染物预报常用的预报时间间隔为1 h, 故将模型输出按所处时间段进行平均, 转化为小时值输出, 预测模型结构如图 7所示.模型实际应用时可立足于环保监管部门, 通过数据接口获取城区各监测站点的监测数据, 同步接入气象预报和交通流量预报数据, 运行模型后, 得到预测结果, 并在后续的监测中不断优化模型, 实现NOx浓度的精准预测, 为后续管控机动车尾气污染提供相应支撑.本文采用2016年6月1日—8月24日的监测站数据和车流量数据, 将前80%的数据划分为训练集, 后20%的数据划分为测试集.
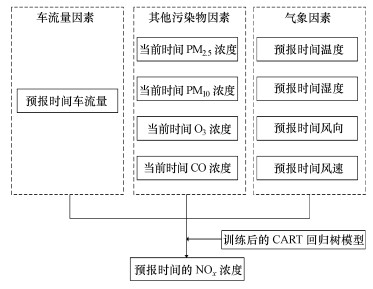 |
| 图 7 基于CART回归树算法的NOx浓度预测模型(预报时间为当天时间的后一天) Fig. 7 Prediction model of NOx concentration based on decision tree algorithm |
为准确评判模型的预测性能, 选取平均绝对误差(Mean Absolute Error, MAE)、均方误差(Mean Square Error, MSE)及可决系数R2作为模型性能的评价指标, 三者表达式如下:
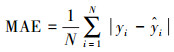
|
(7) |
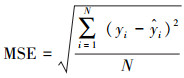
|
(8) |
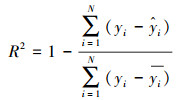
|
(9) |
式中, yi为实际NOx浓度值, 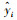
为检验CART回归树算法的预测性能, 本文将之与BP神经网络和支持向量机进行对比.因利用机器学习算法预测空气中NOx浓度的例子较少, 故参考预测PM2.5浓度的文献, 建立BP神经网络模型(王敏等, 2013)和支持向量机模型(谢永华等, 2015)进行实例对比, 3个模型的训练集与测试集数据均一致.为了解3个模型的预测值与实际值的偏离程度, 以各个模型的残差值(实际值与预测值的差)进行对比.
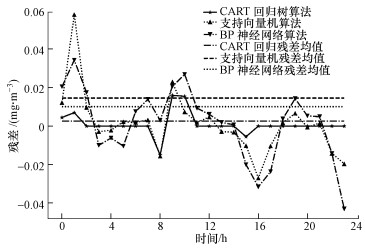
以测试集中随机抽取一天的残差图和全部测试集(16 d)的残差图分析3个模型的准确性与稳定性.由图 8可以发现, CART回归树算法的预测残差值始终在零点附近波动, 波动范围较小, 而支持向量机和BP神经网络的预测残差值则波动较大, 从3条残差均值线可直观地看出3个模型的预测残差大小.结合图 9全部测试集的预测残差图发现, 相比于另两种算法, CART回归树算法的预测精度在随机的一天和全部测试集中均更高.
 |
| 图 8 24 h预测残差对比 Fig. 8 Comparison of predicted residuals for 24 hours |
 |
| 图 9 全部测试集的预测残差对比 Fig. 9 Forecast residuals comparison for all test sets |
为准确的量化、评价3种模型的预测性能, 以3.1节中所列的3个评价指标对预测结果进行评价分析, 根据3个评价指标的公式计算出的评价结果如表 1所示.从表 1可以看出, CART回归树算法预测结果中各项评价指标均优于支持向量机和BP神经网络.CART回归树算法的MAE值最小说明其预测偏离程度最低, MSE值最低说明其预测的平均误差可靠程度最高.CART回归树算法的R2达到了0.9252, 比BP神经网络和支持向量机分别高13%和21%, 说明CART回归树算法的预测值与实际值的拟合程度较好, 预测更准.综上所述, 在相同的数据训练下, CART回归树算法的预测性能比支持向量机和BP神经网络的预测性能更好.
| 表 1 3种预测方法预测性能评价对比 Table 1 Comparison of three prediction methods for predicting performance evaluation |
对城市空气污染物而言, 城市活动与大气环境因素共同影响着其形成与扩散, 特殊活动期间, 为保障活动期间的空气质量, 会采取相应的临时管控措施, 所以特殊活动期间污染物相应的影响因素会发生较大变化, 预测模型在特殊活动期间能否保持较高的预测精度也是模型一个重要的考察指标.
2016年9月4日—5日G20峰会于杭州召开, 政府部门采取了多项措施保障会议期间的空气质量, 根据《G20峰会浙江省环境保障工作方案》要求, 会议保障阶段为8月24日—9月6日, 保障时期分3个阶段实施递进式管控措施(赵军平等, 2017), 保障期间NOx相应的影响因素发生了较大变化.为验证该NOx预测模型在此期间是否仍具有较好的预测精度, 以会议期间的相关数据对模型进行进一步验证.
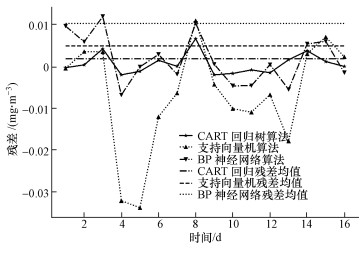
设定当前时间为9月3日, 预报次日NOx的小时值浓度, 将相应数据输入模型后得到次日全天NOx浓度小时值, 同时利用支持向量机和BP神经网络预测NOx浓度小时值, 得到3个模型的预测残差图, 并从上节测试集中随机抽取一天进行对比, 结果如图 10所示.
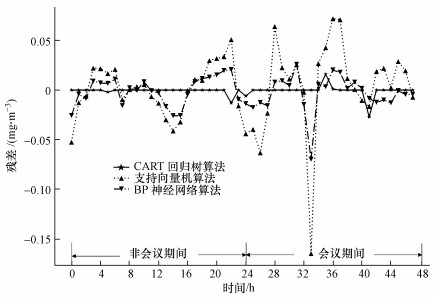 |
| 图 10 会议期间与非会议期间预测残差对比 Fig. 10 Predictive residual comparison between meetings and non meetings |
图 10中前24 h为测试集中随机选取的一天, 后24 h为9月4日当天, 纵坐标为残差值.从图中可以发现, CART回归树算法模型不仅在非会议期间预测性能比另两种模型要好, 在会议期间, CART回归树算法模型同样具有良好的预测精度, 残差波动最小.而支持向量机算法模型与BP神经网络模型在会议期间的预测性能则远不及非会议期间, 两者在会议期间当天8:00前后的预测出现较大偏差, 远超过非会议期间的平均水平.可见在G20会议期间, 因临时管控措施的实施, 期间的NOx影响因素出现较大变化, 支持向量机模型和BP神经网络模型不能够适应此类输入条件变化较大的情况, 而CART回归树模型在此类情况下仍具有较好的预测效果, 其预测值MSE值为3.2708×10-5, MAE值为3.1208×10-3, R2为0.9153, 与非会议期间的预测性能相差不大.
4 结论(Conclusions)1) 本文构建了数据预处理方法, 对异常数据进行剔除与修复, 有效地提升了样本数据质量.
2) 对影响NOx浓度的相关因素进行分析, 结果发现, 气象因素中的风向和风速是影响NOx消散的主要因素, 相关系数分别达到-0.3780和-0.3164;其它污染物因素中CO浓度与NOx浓度相关系数最大, 达到0.5926, 其次为O3浓度, 相关系数为-0.4037.
3) 本文提出了基于CART回归树算法的NOx浓度预测模型, 经实例验证, 与BP神经网络预测模型和支持向量机预测模型相比, CART回归树预测模型的预测性能优于另外两种模型, R2分别提升了13%和21%.
4) 利用G20峰会期间的实验数据, 验证了CART回归树预测方法较BP神经网络和支持向量机在特殊活动期间仍具有较好的预测水平, 可以适应不同条件下的预测需求.
陈亚玲, 赵志杰. 2013. 基于小波变换与传统时间序列模型的臭氧浓度多步预测[J]. 环境科学学报, 2013, 33(2): 339–345.
|
Dhyani R, Sharma N, Maity A K. 2017. Prediction of PM2.5 along urban highway corridor under mixed traffic conditions using CALINE4 model[J]. Journal of Environmental Management, 198: 24–32.
|
Grivas G, Chalouakou A. 2006. Artificial neural network models for prediction of PM10 hourly concentrations, in the Greater Area of Athens, Greece[J]. Atmospheric Environment, 40(7): 1216–1229.
DOI:10.1016/j.atmosenv.2005.10.036
|
Khreis H, Kelly C, Tate J, et al. 2017. Exposure to traffic-related air pollution and risk of development of childhood asthma:a systematic review and meta-analysis[J]. Environment international, 100: 1–31.
DOI:10.1016/j.envint.2016.11.012
|
Hsu Y, Tsai J, Chen H, et al. 2001. Tunnel study of on-road vehicle emissions and the photochemical potential in Taiwan[J]. Chemosphere, 42(3): 227–234.
DOI:10.1016/S0045-6535(00)00074-6
|
姜宛贝, 孙强强, 曲葳, 等. 2016. 基于多季相光谱混合分解和决策树的干旱区土地利用分类[J]. 农业工程学报, 2016, 32(19): 1–7.
DOI:10.11975/j.issn.1002-6819.2016.19.001 |
苗蕾, 廖晓农, 王迎春. 2016. 基于长时间序列的北京PM2.5浓度日变化及气象条件影响分析[J]. 环境科学, 2016, 37(8): 2836–2846.
|
Dhyani R, Sharma N, Maity A K. 2017. Prediction of PM2.5 along urban highway corridor under mixed traffic conditions using CALINE4 model[J]. Journal of Environmental Management, 198: 24–32.
|
宋从波, 李瑞芃, 何建军, 等. 2016. 河北廊坊市区大气中NO、NO2、和O3污染特征研究[J]. 中国环境科学, 2016, 36(10): 2903–2912.
DOI:10.3969/j.issn.1000-6923.2016.10.004 |
孙宝磊, 孙暠, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 2017, 37(5): 1864–1871.
|
Tehrany M S, Pradhan B, Jebur M N. 2013. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS[J]. Journal of Hydrology, 504: 69–79.
DOI:10.1016/j.jhydrol.2013.09.034
|
王黎明, 吴香华, 赵天良, 等. 2017. 基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案[J]. 环境科学学报, 2017, 37(4): 1268–1276.
|
王翔, 陈小鸿, 杨祥妹. 2015. 基于K最邻近算法的高速公路短时行程时间预测[J]. 中国公路学报, 2015, 28(1): 102–112.
DOI:10.3969/j.issn.1001-7372.2015.01.014 |
王敏, 邹滨, 郭宇, 等. 2013. 基于BP人工神经网络的城市PM2.5浓度空间预测[J]. 环境污染与防治, 2013, 35(9): 63–66, 70.
DOI:10.3969/j.issn.1001-3865.2013.09.013 |
徐鹏, 郝庆菊, 吉东生, 等. 2016. 重庆市北碚大气中PM2.5、NOx、SO2和O3浓度变化特征研究[J]. 环境科学学报, 2016, 36(5): 1539–1547.
|
谢永华, 张鸣敏, 杨乐, 等. 2015. 基于支持向量机回归的城市PM2.5浓度预测[J]. 计算机工程与设计, 2015, 36(11): 3106–3111.
|
杨强, 黄成, 卢滨, 等. 2017. 基于本地污染源调查的杭州市大气污染物排放清单研究[J]. 环境科学学报, 2017, 37(9): 3240–3254.
|
严仁嫦, 叶辉, 林旭, 等. 2018. 杭州市臭氧污染特征及影响因素分析[J]. 环境科学学报, 2018, 38(3): 1128–1136.
|
叶贤满, 徐旭, 洪盛茂, 等. 2015. 杭州市大气污染物排放清单及特征[J]. 中国环境监测, 2015, 31(2): 5–11.
DOI:10.3969/j.issn.1002-6002.2015.02.002 |
张秀英, 孙棋, 王柯, 等. 2008. 基于决策树的突然Zn含量预测[J]. 环境科学, 2008, 29(12): 3508–3512.
DOI:10.3321/j.issn:0250-3301.2008.12.036 |
张棪, 曹健. 2016. 面向大数据分析的决策树算法[J]. 计算机科学, 2016, 43(6A): 374–379.
DOI:10.11896/j.issn.1002-137X.2016.6A.089 |
赵建华, 陈汉林, 杨树锋. 2006. 滑坡灾害危险性评价模型比较[J]. 自然灾害学报, 2006, 15(1): 128–134.
DOI:10.3969/j.issn.1004-4574.2006.01.021 |
赵军平, 罗玲, 郑亦佳, 等. 2017. G20峰会期间杭州地区空气质量特征及气象条件分析[J]. 环境科学学报, 2017, 37(10): 3885–3893.
|
朱亚杰, 李琦, 侯俊雄, 等. 2016. 运用贝叶斯方法的PM2.5浓度时空建模与预测[J]. 测绘科学, 2016, 41(2): 44–48.
|
 2019, Vol. 39
2019, Vol. 39


