环境科学学报  2019, Vol. 39 Issue (6): 2053-2070
引用本文
李祚泳, 汪嘉杨, 徐源蔚. 2019. 规范变换与误差修正结合的环境系统的前向网络和投影寻踪预测模型[J]. 环境科学学报, 39(6): 2053-2070.
Li Z Y, Wang J Y, Xu Y W. 2019. Forward network and projection pursuit for environmental system prediction based on combination of standard transformation and error correction[J]. Acta Scientiae Circumstantiae, 39(6): 2053-2070.
规范变换与误差修正结合的环境系统的前向网络和投影寻踪预测模型    [PDF全文]
李祚泳 , 汪嘉杨 , 徐源蔚     
成都信息工程大学 资源环境学院, 成都 610225
收稿日期: 2018-04-15; 修回日期: 2018-08-15; 录用日期: 2018-08-15
基金项目: 国家自然科学基金（No.51679155）
作者简介: 李祚泳(1944—),男,教授,E-mail: lizuoyong@cuit.edu.cn
通讯作者（责任作者）: 李祚泳
摘要: 为了建立适用于环境系统的结构简洁、形式统一、程序规范、应用普适的神经网络和投影寻踪回归预测模型，针对传统的神经网络和投影寻踪回归用于多因子、大样本预测建模，存在模型结构复杂、学习效率低的局限，提出设置环境系统预测量及其影响因子参照值和规范变换式的原则和方法，使规范变换后的影响因子皆"等效"于同一个规范影响因子，从而将多因子的的预测建模简化为等效规范因子的预测建模，使模型结构得到极大地简化，提高了学习效率；此外，为了提高预测模型的预测精度，还提出了对预测样本的模型输出值的误差修正公式.在对环境系统的预测量及其影响因子进行规范变换的基础上，将m个规范影响因子的每个建模样本组成m个"等效"训练样本，应用免疫进化算法优化模型参数，分别建立适用于环境系统的2个或3个规范影响因子的前向神经网络和投影寻踪回归两类预测模型；并依据误差理论，对误差修正公式修正后的模型预测精度的提高进行了严格的数学论证.将基于规范变换与相似样本误差修正相结合的两类预测模型，用于某市5个点位的SO2浓度预测，并与6种传统预测模型和方法的预测结果进行了比较.结果表明：对同一个预测样本，同类模型的两种不同结构的的预测值及其相对误差都几乎完全相同或彼此相差甚小；此外，两种不同结构的两类预测模型用于5个样本预测，其相对误差绝对值的平均值分别为2.59%、2.67%；2.18%、2.62%，均远小于传统BP神经网络模型的25.72%、传统PPR模型的14.20%、传统SVR模型的22.13%、模糊识别模型的21.57%、组合算子模型的18.36%和多元回归模型的25.31%；而两类模型预测的最大的相对误差绝对值分别为4.11%和3.57%，更加远远小于传统的6种预测模型的37.18%、56.07%、27.40%、32.14%、38.38%和60.26%.实例分析结果证实了误差修正公式对提高模型预测精度具有切实可行性.基于规范变换与误差修正相结合的前向神经网络和投影寻踪回归两类预测模型不仅避免了"维数灾难"，提高了学习效率和模型的预测精确度，而且具有简洁、普适、规范、统一和稳定的特点，对其他预测建模也有借鉴作用.
关键词: 环境系统     规范变换     预测模型     前向神经网络     投影寻踪回归    
Forward network and projection pursuit for environmental system prediction based on combination of standard transformation and error correction
LI Zuoyong , WANG Jiayang, XU Yuanwei    
College of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225
Received 15 April 2018; received in revised from 15 August 2018; accepted 15 August 2018
Abstract: The purpose of this study was to establish prediction models of neural network and projection pursuit regression for environmental system, which have the charactertctics of simple structure, unified form, standardized procedures and universal application. The predictive models of traditional neural network and projection pursuit regression, which are used in multi-factor and large sample numbers, have limits of complex model structure, low learning efficiency. Therefore, the design principles and methods of reference values and the standard transformation formula used predicting variable and its influencing factors were proposed. The normalized influence factors were equivalent to the same normative influence factor. Thus, the predictive modeling of multiple factors is simplified as the predictive modeling of the "equivalent" norm factor, which greatly simplifies the model structure and improves the learning efficiency. In addition, in order to improve the prediction accuracy of the prediction model, the error correction formula for the model output value of the prediction sample was also proposed. On the basis of standard transformations for the predictive variable and its influencing factors of environment system, each modeling sample with m canonical influence factors were formed m "equivalent" training samples. Then, the immune evolutionary algorithm was used to optimize the model parameters, two different structures of prediction models of forward neural network and projection pursuit regression for environment system prediction were built:the case of 2-2-1 structure, which was used to any 2 normative impact factors and the case of 3-2-1 structure was, which was used to any 3 normative impact factors. Furthermore, based on the error theory, a rigorous mathematical demonstration was made for the improvement of the prediction accuracy of the model by the error correction formula. Two kinds of prediction models based on standard transformation and similar sample error correction were applied to predict the SO2 concentration of 5 spots in a city. Results were compared with the prediction results of six traditional prediction models and methods. The results show that for the same forecast sample, the predicted values and relative errors of two different structures of the same model (forward neural networks or projection pursuit regression) were almost identical or very small. In addition, two kinds of prediction models with two different structures were used for the prediction of 5 samples, and the means of relative error absolute values were 2.59%, 2.67% and 2.18%, 2.62%, respectively. They were far less than the results of 22.13%, 25.72%, 14.20%, 21.57%, 18.36% and 25.31% of the prediction models of traditional BP neural network(BP), traditional projection pursuit regression(PPR), traditional support vector machine(SVM), fuzzy recognition, combination operator and multiple regression respectively. The maximum relative error absolute values of samples of the two prediction models were 4.11% and 3.57%, respectively. They were smaller than the results of 56.07%, 27.40%, 37.18%, 32.14%, 38.38% and 60.26% of six traditional forecasting models. The example analysis results confirm that the error correction formula is feasible for improving the prediction accuracy of the model. Two prediction models of forward neural network and projection pursuit regression based on the combination of standard transformation and error correction can avoid the "dimension disaster", improve the learning efficiency and model prediction accuracy. They have the characteristics of simplicity, universality, standardization, unity and stability. They can also be used for reference in other forecasting models.
Keywords: environmental system     canonical transformation     prediction model     forward neural network     projection pursuit regression    
1 引言(Introduction)

长期以来, 人们经过认真思索, 达成共识：即人类不仅要重视环境的现状, 更应关注环境的未来.为此, 国内外学者提出了许多用于环境系统预测的模型和方法, 如多元线性回归分析(Comrie, 2013; 黄思等, 2015)、分段线性的最近邻表示算法(王保良等, 2016)、非线性灰色伯努利算法(NGBM)(Chen, 2008)、Fuzzy分析((Chen et al., 2005)、灰色分析(肖鸣等, 2017)、灰色马尔柯夫趋势分析(邹志红等, 2009)、时序分析(Diaz Robles et al., 2008)、小波分析(Lange et al., 2007.)、集对分析(金菊良等, 2009)、可变集分析(Chen et al., 2013)等确定性或不确定性分析预测模型, 以及投影寻踪回归(projection pursuit regression, PPR)(Qi et al., 2008)、多种神经网络(neural network, NN) (Grivas et al., 2006; Ghose et al., 2010; Paschalidou et al., 2011; 杨云等, 2016; 孙宝磊等, 2017)和支持向量机(support vector machines, SVM)(Ortiz Garcia et al., 2010; 笪英云等, 2015; Park et al., 2015; Moazami et al., 2016; Shaban et al., 2016)等智能优化预测模型.在多种预测模型中, 最常用的是神经网络、投影寻踪回归和回归支持向量机等预测模型.

传统的回归支持向量机(support vector regression, SVR)预测模型在防止过拟合、克服局部极值及不受高维、非线性和小样本数的限制等方面具有明显优势(Noori et al., 2012), 但对多因子、大样本数的预测问题, 不仅模型结构和计算的复杂性迅速增大, 而且收敛速度慢、求解精度低, 尤其不能建立适用于不同样本数和因子数的普适、规范和统一的模型(李祚泳等, 2018).为此, 笔者提出将规范变换与相似样本误差修正法相结合的回归支持向量机预测模型, 简化了SVR预测模型的结构, 提高了模型学习效率和模型求解精度(李祚泳等, 2018).传统的神经网络和投影寻踪回归预测模型虽然各有其优点, 但对多因子、大样本数的预测建模, 皆存在学习效率低、泛化能力差、求解精度低、模型结构复杂和计算难度皆较大等问题(Wang et al, 2004), 即存在“维数灾难”.传统的神经网络和投影寻踪回归预测模型同样不能建立适用于不同样本数和因子数的形式统一、结构普适、程序规范的预测模型, 从而使它们的应用受到极大的限制.传统的预测模型还普遍存在模型的稳定性较差和预测精度不高.

与将规范变换和相似样本误差修正法相结合用于回归支持向量机预测建模类似, 若对环境系统预测变量及其影响因子进行规范变换, 使规范变换后的所有影响因子皆“等效”于同一个规范影响因子, 将多因子的高维复杂预测建模问题简化为仅是对等效规范因子的简单低维预测建模问题; 此外, 用相似样本的误差修正法对预测样本的模型输出进行误差修正, 以提高两种预测模型对样本(尤其是过拟合样本和异常样本)的预测精度.二者结合用于某市SO2预测的效果检验表明：模型不仅避免了“维数灾难”, 提高了学习效率和预测精度, 而且编程和计算比传统的PPR、BP网络和NV-SVR预测模型都简便.对5个样本预测的相对误差绝对值的平均值和最大的相对误差绝对值都远小于传统的PPR、BP网络、SVR、模糊识别、参数化组合算子、多元回归预测模型的预测结果, 对提高过拟合样本和异常样本的预测效果尤其显著.

2 预测量及其影响因子的规范变换(Canonical transformations of predictive variables and their influencing factors)

传统的预测模型的预测变量及其影响因子通常采用的归一化或标准化变换皆是各自独立的线性变换, 因而变换前、后影响因子的个数及数据变化特性皆不会发生改变.若对预测变量及其影响因子采用如式(1)和式(2)所示的规范变换(李祚泳等, 2018), 此规范变换要求变换后的样本预测变量及各影响因子的最小规范值x′jm(或yjm′)和最大规范值xjM′(或yjM′)分别被限定在[0.15, 0.30]和[0.40, 0.55]较小范围内, 并能使规范变换后的不同影响因子规范值皆呈近似相同的变化规律.因而该变换的特点是：变换后用规范值表示的各因子之间不再彼此独立, 而有相互关联.因此, 规范变换后的所有影响因子可视为“等效”于同一个规范影响因子, 从而将多因子的高维复杂预测建模问题简化为仅是对“等效”规范因子的简单2维或3维的预测建模问题, 使传统的预测模型结构得到极大简化.因子“等效”的含义是指规范变换后的所有因子的规范值(数据)不仅分布规律、变化特性呈近似正态分布, 而且它们的分布参数(数学期望和方差)差异很小, 十分接近.因而, 用规范值表示的每个因子对预测变量的影响大小近似相同, 即完全“等效”.

(1)
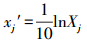
(2)

式中, cj为因子或预测变量实际值; cj0为设置的因子或预测变量的参照值; cjb为设定的因子或预测变量的阈值; Xj和xj′分别为因子或预测变量的变换值和规范值; k代表全体样本个数; nj为如式(3)所示的因子或预测变量的幂指数.式(1)右边1~4行适用于正向类因子或预测变量的变换; 5~8行适用于逆向类因子或预测变量的变换.

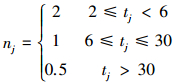
(3)

式中, tj为因子或预测量实际值的最大值与最小值之比值, 如式(4)所示.

(4)

变换式(1)中的参数cjb、nj和cj0的确定过程如下：

第一步, 确定因子j是否需要设置cjb.有以下两种情况的正向、逆向因子, 需要设置cjb：1)原始数据中有cj≤ 0的因子, 其目的是使所有样本的该因子值全变为正值, 即有cj-cjb>0 (对正向型因子)或cjb-cj>0 (对逆向型因子); 2)用式(4)右边第1行的判定条件计算得到的tj < 2的因子, 其目的是使再用式(4)右边第2行的判定条件计算得到该因子的tj>2.对cjb取值的限制条件为：对正向型因子, cjb < min{cj}; 对逆向型因子, cjb > max{cj}.

第二步, 确定nj：由式(4)计算出tj, 再根据式(3)确定nj的取值.

第三步, 确定因子的cj0：首先, 在[0.15, 0.30]区间中值的邻域内, 随意设置因子最小规范值x′jm(比如令x′jm= 0.20), 将第二步已确定的nj及设置的x′jm和min{cj}(或还有cjb)代入式(1)和(2)中, 进行逆运算, 求解出cj0; 再将求得的cj0、nj和max{cj}(或还有cjb)值代入式(1)和(2)中, 计算得到最大规范值x′jM.若x′jM在[0.40, 0.55]内, 则cj0即为确定的参照值; 否则, 需对cj0作微调, 再重复上述过程, 直到最小规范值x′jm和最大规范值x′jM能分别在被限定的较小范围内即可.现举例说明如下：

例1某市1994—2000各年住户用气普及率(cj)的调查统计数据为：56.17、52.10、46.40、49.20、53.02、55.20、59.14.

1) 确定该因子是否需要设置cjb：由于该因子tj= 59.14/ 46.40=1.27 < 2, 故需要设置cjb.又因该因子与该市空气清洁指数成正相关(正向型因子), 因此, 变换式(1)应设计为：

Xj= ((cj-cjb)/ cj0)nj, 而且应有cjb < 46.40.若设cjb= 40.

2) 确定nj：在cjb= 40情况下, 最大值和最小值分别变为59.14-40=19.14和46.4-40=6.4, 从而tj= 19.14/ 6.40=2.99>2, 由式(3)右边第1个判别条件确定nj=2;

3) 确定cj0：在(0.15, 0.30)内, 若设置与因子最小数据(cjm=46.40)相应的最小规范值为x′jm= 0.20, 则将cjm=46.40、cjb= 40、nj=2和x′jm= 0.20代入规范变换式(1)和(2)中进行逆运算, 计算得到cj0=2.35.

4) 验证当cj0=2.35时, 与因子最大数据(cjM=59.14)相应的最大规范值为x′jM是否在限制范围内：将cjM=59.14、cjb= 40、nj=2和cj0=2.35代入规范变换式(1)和(2)中进行运算, 计算得到最大规范值为xjM′= 0.4195, 因为0.40 < 0.4195 < 0.55, 故设置cj0=2.35是合理、可行的.

3 基于规范变换的两种预测模型(Two prediction models based on canonical transformation) 3.1 规范变换的前向神经网络预测模型

为使规范变换的前向神经网络(forward neural network of normalized value, NV-FNN)模型的功能更强大和加速收敛, 采用双极性sigmoid函数作为隐层节点的激活函数; 此外, 为使模型结构既简化, 又能保持较强的非线性映射能力, 采用对隐节点输出的线性求和计算.满足此两个条件的NV-FNN预测模型如式(5)所示(李祚泳等, 2015).

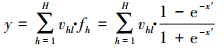
(5)

式中, y为样本的模型输出; H为隐层节点数目; fh为样本在隐节点h的输出; vhl为隐节点h与输出节点l的连接权值, 通常取l=1, 故l可略去; x′为样本的输入矢量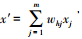, 其中, whj为输入节点j与隐节点h的连接权值, xji′为由式(1)和式(2)计算得到样本i的影响因子j的规范值, 亦即NV-FNN模型的输入; m为影响因子数目, 也是输入节点数目.

由于规范变换后的m个因子完全“等效”, 因此, 只需构建两种最简结构的2-2-1(2个输入节点、2个隐节点和1个输出节点)或3-2-1(3个输入节点、2个隐节点和1个输出节点)的前向网络预测模型的表示式, 如式(6)和式(7)所示.由于式(6)和式(7)对所有m个“等效”规范因子皆适用, 因而, 此2种最简结构的预测模型不仅克服了“维数灾难”, 而且具有普适性、规范性和统一性.

(6)
(7)

式中, vh(h=1, 2)和whj(h=1, 2; j=1, 2, 3)皆为需要用优化算法(比如免疫进化算法)优化确定的网络连接权值.

3.2 规范变换的投影寻踪回归预测模型的矩阵表示

投影寻踪是一种依据“审视数据——计算机模拟——预报”探索性数据分析的预测建模思想(EDA)和计算技术.投影寻踪回归(projection pursuit regression, PPR)实质是用N个岭函数Gm(Zm)的“和”去逼近回归函数, 其特点是：它无论对线性还是非线性、正态还是偏态、独立还是相关、低维还是高维分布数据皆适用.规范变换的投影寻踪回归(projection pursuit regression of normalized value, NV-PPR)分析模型也是用N个岭函数Gm(Zm)的“和”去逼近回归函数y, 它可写成如式(8)所示的参数矩阵乘积表示式(李祚泳等, 2007).

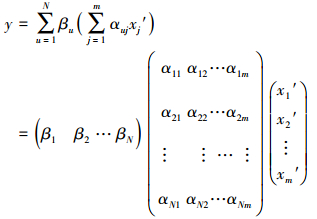
(8)

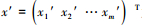
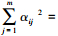
式中, 为m维自变量(即因子)规范值组成的列矩阵(列向量)(m行1列); “T”表示矩阵转置; α是由N个m维投影方向矢量构成的矩阵(N行m列), 它的每一行是m维投影方向矢量组成的行矩阵(行向量), 需满足1; Guα·x′为第u个岭函数(u=1, 2, …, N), 它就是α矩阵的第u行与m个自变量(因子)组成的列矩阵x′的乘积表示式; ;βu为第u个岭函数的权重系数; N为岭函数的个数, 它为等于或大于2的正整数.岭函数的“个数”类似于前向神经网络(FNN)或者BP神经网络模型隐层(中间层)的隐节点的“个数”.因此, N个岭函数的和也就是由N行m列的矩阵α与m行1列的列矩阵x′的乘积矩阵.由于岭函数的个数N需随样本的影响因子数目的增加而增加, 因而当因子较多时, 需要优化的参数矩阵元随N的增加而激剧增长, 即出现通常所说的“维数灾难”.这也许就是传统的PPR多因子预测模型不仅编程复杂、学习效率低、收敛速度慢, 而且预测精度往往不高的原因之一.传统的PPR预测模型岭函数的个数N采用尝试法(试奏法)或用优化方法确定; 而基于因子规范变换的PPR预测模型由于任意多个因子皆用一个等效规范因子替代, 因子数目极大减少, 故只需构造N=2个岭函数就足够了, 不需要用其他方法确定, 从而使NV-PPR预测模型不仅编程简单、学习效率高, 而且预测精度也高, 避免了“维数灾难”.

与NV-FNN预测建模完全类似, 只需分别构建适用于2个规范因子的具有2个岭函数和1个输出变量的2-2-1结构的NV-PPR(2)模型, 和3个规范因子的具有2个岭函数和1个输出变量的3-2-1结构的NV-PPR(3)模型, 如式(9)和式(10)所示; 化简二式, 分别得式(11)和式(12).式(9)~式(12)的预测模型也不仅克服了“维数灾难”, 而且也具有普适性、规范性和统一性.

(9)
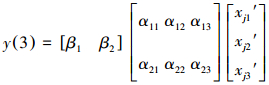
(10)
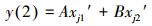
(11)
(12)

式中, A= β1α11+β2α21  B= β1α12+β2α22  C=β1α13+β2α23

式中, xjj′′的第一个字母下标j代表的就是式(8)中的下标j(j=1, 2, …, m); 而第二个数字下标j′ (j′=1, 2, 3)则表示：对由m个规范因子构成的每个建模(或检测)样本, 若将其m个规范因子按序排列, 并首尾相连.当第一个字母下标j代表的因子取定后, 从它开始依顺序取连续3个因子规范值, 记为x′j1、x′j2、x′j3.对NV-PPR(2)模型, 以它们中的相邻2个因子组合成1个训练样本; 对NV-PPR(3)模型, 以它们中的相邻3个因子组合成1个训练(或检测)样本.但无论是NV-PPR(2)模型或NV-PPR(3)模型, 每个建模样本都要依顺序构造出m个训练(或检测)样本, 而全部n个建模样本共构造出m×n个训练(或检测)样本.βu(u =1, 2)和αuj(u=1, 2;j=1, 2, 3)分别为需要用优化算法优化确定的岭函数的权重系数和投影方向单位矢量的各个分量.

3.3 预测模型的优化目标函数式

为了优化NV-FNN和NV-PPR预测模型中的参数vh(h=1, 2)、whj(h=1, 2;j=1, 2, 3)和βu(u=1, 2)、αuj(u=1, 2;j=1, 2, 3), 设计如式(13)所示的优化目标函数式(李祚泳, 2018).

(13)

式中, yij为由NV-FNN模型式(6)、式(7)或NV-PPR模型(9)、式(10)计算得到的第i(i=1, 2, …, n)个建模样本组成的第j个训练样本的模型输出值.对有m个规范因子的n个样本的预测建模而言, 由于每个建模样本需要组成的训练样本数与因子数都同是m个, 因此, 训练样本数亦可用j(j=1, 2, …, m)表示, 而n个建模样本共组成m×n个训练样本.yi′为建模样本i组成的任意一个训练样本的模型期望输出值.第i个建模样本组成的m个训练样本的模型期望输出值皆相同, 即为该样本预测量yi的规范值yi′.

3.4 预测样本模型输出的误差修正式

为使预测样本尤其是过拟合样本和异常预测样本(或检测样本)的预测(或检测)值更接近实际值, 多数情况下, 需对预测(或检测)样本的模型输出值进行误差修正.此处提出的误差修正的基本思想为：依据相似原因产生相似结果的原则, 从建模样本集中, 找出与预测(或检测)样本的模型计算输出值最接近的一个或多个模型计算输出值相似的样本, 并认为这些相似样本的模型计算输出值及拟合相对误差应分别与该预测(或检测)样本的模型计算输出值和估计相对误差成比例, 因而满足如式(14)所示的比例基本定理公式, 从而计算得到预测样本的模型输出值yx′的估计相对误差rx′, 再由估计相对误差rx′计算预测样本修正后的模型输出值yxx′, 如式(15)所示(李祚泳等, 2018).

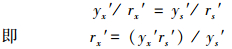
(14)
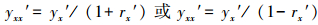
(15)

式中, yx′和yxx′分别为预测(或检测)样本修正前和修正后的模型计算输出值; rx′为计算得到预测(或检测)样本模型输出的估计相对误差的绝对值; ys′和rs′分别为在建模样本集中, 与预测(或检测)样本的模型输出值yx′最接近的一个或多个相似样本的模型拟合输出值及拟合相对误差的绝对值.

对模型计算输出值误差修正公式(15)的两种情况的采用说明如下：由于预测(或检测)样本的模型计算输出值yx′与相似样本的模型计算输出值ys′很接近, 而相似样本的模型计算输出的理想(目标)值应为该相似样本的实际值ys的规范值ys0′, 因此, 通常情况下, 依据它们之间的相互大小关系来选用：1)若yx′~ys′, 且yx′> ys0′和ys′> ys0′, 则因yx′和ys′都大于理想值ys0′, 故需用公式yxx′= yx′/ (1+ rx′)修正, 使修正后的预测样本模型输出值yxr′减小; 2)若yx′~ys′, 且yx′ < ys0′和ys′ < ys0′, 则因yx′和ys′都小于理想值ys0′, 故应用公式yxx′= yx′/ (1- rx′)修正, 使修正后的预测样本模型输出值yxx′增大.3)若yx′~ys′~ ys0′, 且rs′很小(比如rs′ < 0.5%), 若只有此一个相似样本, 表示三者差异很小, 误差可以忽略不计, 可不作误差修正; 当有多个相似样本, 而其他相似样本的误差rs′又不可忽略时, 此相似样本的rs′虽然很小, 则需兼顾其他相似样本的误差修正情况, 选择其中一个公式修正.4)若yx′~ys′, 且rs′较大(比如rs′>15%), 说明此相似样本可能是“过拟合”样本或异常样本, 当只有此一个相似样本：若用式yxx′= yx′/ (1- rx′)计算出的yxx′较大, 比如yxx′>0.55(上限值), 而用式yxx′= yx′/ (1+ rx′)计算出的yxx′值在[0.20, 0.45]范围内, 则用后者公式修正; 反之, 若用式yxx′= yx′/ (1+ rx′)计算出的yxx′较小, 比如低于yxx′ < 0.20(下限值), 而用式yxx′= yx′/ (1- rx′)计算出的yxx′值在[0.30, 0.55]范围内, 则用后者公式修正; 当还有其他相似样本, 则也需兼顾其他相似样本的误差修正情况, 选择其中一个公式修正.5)有多个相似样本时, 一般是将他们修正后的输出值的均值作为最终的输出修正值.

3.5 两种预测模型的建模实现过程

两种预测建模的具体实现过程如下：

① 依据规范变换式的设计原则和方法, 设置预测变量及其影响因子的规范变换式(1)和(2), 并计算出因子和预测变量的规范值;

② 分别将因子和预测变量的规范值代入两种模型的公式(6)、(7)或式(9)、(10)和目标函数式(13), 应用优化方法对公式中的参数进行优化;

③ 用优化好的公式, 计算两种模型的建模样本的模型拟合输出值及其拟合相对误差绝对值和检测(预测)样本的模型输出值;

④ 为提高预测样本尤其是过拟合样本和异常预测样本的预测精度, 用相似样本误差修正公式(式(14)和(15))对预测样本模型输出值进行误差修正;

⑤ 最后由修正后的预测样本的模型输出值, 用规范变换式的逆运算, 计算出样本预测值.

4 预测模型的检验(The test of prediction model)

预测模型的检验包括对模型的可靠性检验和对模型的精确度检验.

4.1 预测模型的可靠性分析

由于任何预测模型都是构筑在若干模型参数基础上的, 这些参数又是依据模型影响因子及其预测变量的输入、输出数据来确定的.而获得的输入、输出数据具有的误差必然导致预测模型的参数估计存在一定的不确定性, 这些参数的不确定性对模型预测结果的可靠性和稳定性当然会有一定的影响.其影响程度即是模型的可靠性, 它可以通过模型的输出对于输入的响应程度(即灵敏度)分析来确定(郑彤等, 2003).依据系统灵敏度定义, 预测模型输出y的相对误差Δy/y和影响因子的相对误差Δcj/cj之间具有如式(16)所示的关系式.

(16)

式中, Sy为NV-FNN和NV-PPR模型的输出y对影响因子cj的灵敏度.

① NV-FNN预测模型的可靠性分析

若变换式(1)中的逆向影响因子的nj用负数表示, 则式(1)可统一用正向影响因子形式表示.将式(1)代入式(2), 得

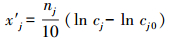
(17)

求上式x′j对cj的微分, 得

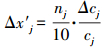
(18)

上式两边同除以x′j, 得

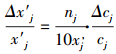
(19)

由双极性函数的输出式

(20)

可得

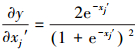
(21)
(22)

比较式(16)和式(22), 可得NV-FNN模型的输出y对影响因子cj的灵敏度为：

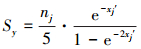
(23)

② NV-PPR预测模型的可靠性分析

完全类似, 两种结构的NV-PPR预测模型输出式(11)和(12)可统一表示为式(24).

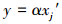
(24)

由式(1)、式(2)和式(24), 可得

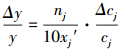
(25)

比较式(16)和式(25), 得

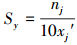
(26)

变换式(1)中的nj只取nj=±2、±1、±0.5.由于用式(1)和(2)计算得到的各因子和预测变量的最小规范值的下限为0.15, 最大规范值的上限为0.55.因此, 任何因子的其余规范值必然满足0.55>xj′>0.15.由式(23)和式(26)可知：当且仅当nj=±2和0.2>xj′>0.15时, 才会出现计算得到的NV-FNN和NV-PPR模型的灵敏度Sy >1, ;其余情况, 皆满足Sy ≤1, 即低灵敏度模型.若因子实际值的相对误差为Δcj/cj, 由式(16)知, (Δy/y)≤(Δcj/cj).可见, NV-FNN和NV-PPR模型计算得到的输出值y的相对误差Δy/y一般不被放大, 反而被缩小.因此, NV-FNN和NV-PPR预测模型的输出是稳定、可靠的.

由式(16)知：每个影响因子的不确定性相对误差Δcj/cj会导致模型预测值y的相对误差Δyj/yj(j =1, 2, …, m), 又依据误差传播理论, m个因子具有的相对误差Δcj/cj(j=1, 2, …, m)导致预测模型输出y总的相对误差Δy/y应为各因子导致的相对误差Δyj/yj(j =1, 2, …, m)绝对值之和, 如式(27)所示.

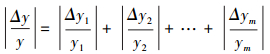
(27)

可见, 当影响因子m较多时, 传统的FNN和PPR预测模型由于模型结构复杂, 需要优化确定的参数多, 其不确定性对模型预测结果的影响也就很大, 因而预测精度低、误差大也就是必然; 而基于规范变换的NV-FNN、NV-PPR预测模型, 由于所有m个规范影响因子等效于一个规范影响因子, 模型结构简化, 优化的参数大大减少, 减少了模型预测的相对误差, 将模型结构对预测精度的影响降低到最小程度, 提高了模型的预测精度.比如, 若每个影响因子的相对误差Δcj/cj都相同, 则m个规范影响因子的规范变换的预测模型输出的相对误差Δy/y仅为传统的FNN和PPR预测模型输出的相对误差的1/m.

4.2 预测模型的精确度F值统计检验

精确度是指模型的计算结果与实际数据之间的吻合程度.常用的模型的精确度F值统计检验通过比较两组数据的方差, 以确定他们的精密度是否有显著性差异, F统计量计算式如式(28)所示.

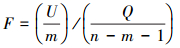
(28)

式中, U和Q分别为样本的回归平方和及残差平方和; m为影响因子数, n为样本数.选择显著水平α=0.005~0.10, 查阅F分布表中自由度n1=m, n2=n-m-1时的临界值F0.005~0.10.若由式(28)计算出的F>F0.005~0.10, 则模型精度得到验证.

4.3 预测模型精确度的理论分析 4.3.1 误差修正公式对模型输出的相对误差的影响

以式(15)的第1个误差修正公式为例, 分析其对预测样本模型输出精度的影响.将式(14)代入式(15)的第1个公式, 得

(29)

定义：预测样本X与其相似的样本S之间的相似度(亦可称相似比)为

(30)

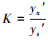
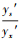
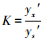
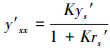
若yx′ < ys′, 则; 若yx′>ys′, 则K=.因此K∈[0, 1], 对相似样本而言, 通常K∈[0.90, 1]内.若yx′ < ys′, 将代入式(29), 化简得

(31)

在K为一定值情况下, 将式(31)中的y′xx对rs′微分得

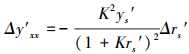
(32)

将式(32)分别除以式(31)的两边, 化简得

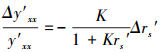
(33)

因为

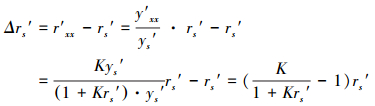
(34)

式(34)代入式(33), 化简得

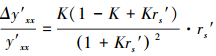
(35)

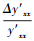
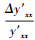
式中, 为用误差修正公式修正后的预测样本模型输出计算值(估计)的相对误差, 简记为r′xx= .为了叙述方便, 以下简称“修正后的样本模型输出的相对误差”.

从式(35)可见, 修正后的样本模型输出的相对误差r′xx仅由相似样本的模型输出的拟合相对误差rs′和预测样本与相似样本之间的相似度K唯一确定.由式(35)计算得到有不同相似度K和不同相似样本的相对误差rs′情况下, 修正后的样本模型输出的相对误差(绝对值)如表 1所示.

表 1 不同K和不同rs′情况下修正后的预测样本模型输出的相对误差 Table 1 Relative errors of modified prediction model output under different K and different rs′ conditions

对式(35)的相对误差r′xx讨论如下：

1) 当预测样本与相似样本完全相似时, K=1, 式(35)简化为：

(36)

2) 式(35)右边rs′前的表示式可改写为：

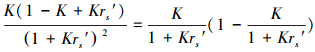
(37)

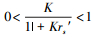
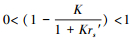
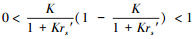
式中, 第1个因子满足; 第2个因子亦满足.因而它们的乘积亦满足, 因此,一定有r′xx<rs′

结论：用误差公式修正后的预测样本模型输出的相对误差一定会小于未用误差公式修正的相似样本的模型输出的相对误差.

3) r′xx随rs′的变化

在相似比K为某一定值情况下, 将式(35)中的r′xx对rs′求偏导数, 并化简得

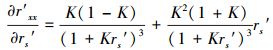
(38)

由于0 < K≤1, 因此, 式(38)右边总满足大于0, 故r′xx是rs′的增函数, 即r′xx随rs′的增大而增大.但随着rs′的增大, 其导数值逐渐变小, 即r′xx增大的速度逐渐减慢; 反之亦然.这同表 1中K为某一定值时的r′xx随rs′的变化规律完全一致.

4) r′xx随K的变化

类似, 在rs′为某一定值情况下, 将式(35)中的r′xx对K求偏导数, 并化简得

(39)

式中, 分子随K增大而减少; 分母随K增大而增大, 因此r′xx是K的减函数, 即修正后的样本模型输出的相对误差r′xx随相似度K的增大而逐渐减小, 反之亦然.这同表 1中当rs′为某一定值时, r′xx随K的变化规律也是完全一致的.

4.3.2 误差修正后的样本模型预测值的相对误差及预测精度分析

对式(1)和式(2)进行逆变换, 得到如式(40)所示的指数变换式.

(40)

式中, cj和x′j的意义同式(1)和式(2);a=cjo, b=.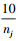

设不用误差公式修正和采用误差公式修正后的预测样本模型输出计算值分别为yx′和y′xx, 将它们分别代入式(40), 得

(41)
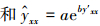
(42)

式中, x和xx分别为不用误差公式修正和用误差修正公式修正后, 计算得到的样本实际预测值.

将式(41)和式(42)的x和xx分别对yx′和y′xx求微分, 可得

(43)
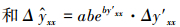
(44)

将式(43)和式(44)两边分别除以式(41)和式(42)两边, 得

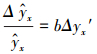
(45)
(46)

由yx′=Kys′, 得Δyx′=KΔys′, 又因Δys′=rs′ys′, 因而有

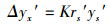
(47)

将式(47)代入式(45), 得

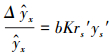
(48)

将式(34)代入式(32)化简, 得

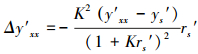
(49)

将式(49)代入式(46), 并取绝对值(为运算简称, 省去绝对值符号, 以下同), 得

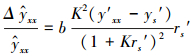
(50)

式(50)的物理意义为：用误差修正公式修正后的样本模型输出值y′xx代入逆规范变换式(42), 计算得到的预测样本实际预测值xx的相对误差与相似样本的模型输出值ys′及其拟合相对误差rs′、相似度K和修正后的样本模型输出值y′xx之间的关系式.

对式(50)讨论如下：

记, 则式(50)还可化为：

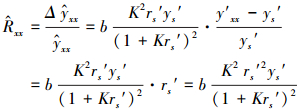
(51)

式中, 因为yx′~ys′, 故yxx′~ys0′.因此, (yxx′~ys′)/ys′可近似用rs′ =(ys0′~ys′)/ys′替代.

1) 当K为某一定值时, 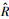xx随rs′的变化

将式(51)中的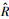xx对rs′求偏导数, 并化简, 得

(52)

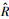
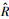
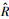
因式(52)右边恒大于0, 故xx是rs′的增函数, 即修正后计算得到的预测样本的实际预测值的相对误差xx随相似样本模型输出计算值的相对误差rs′的增大而增大, 但因导数值随rs′的增大而逐渐减小; 因此, xx的增大量逐渐变小, 反之亦然.

2) 当rs′为某一定值时, 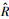xx随K的变化

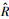
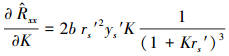
将式(51)中的xx对相似度K求偏导数, 并化简, 得

(53)

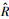
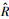
由于式(53)右边恒大于0, 因此, xx亦是K的增函数, 即修正后计算得到的预测样本实际预测值的相对误差xx亦随相似度K的增大而增大.同样, 因导数值随K的增大而逐渐减小, 因而其增大量亦逐渐变小; 反之亦然.

3) 用误差修正公式修正和不用误差修正公式修正计算得到的两种实际预测值的相对误差的大小比较

用式(50)的两边除以式(48)两边, 化简得

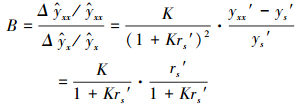
(54)

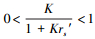
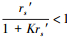
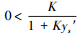
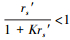
由式(54)计算得到有不同相似度K和不同相似样本的相对误差rs′情况下, 两种相对误差的比值B(或B-1)如表 2所示.因为和0 < , 故它们的乘积亦满足·, 即两种相对误差的比值0 < B < 1.

表 2 不同K和不同rs′情况下修正和未作修正的样本的两种预测值的相对误差的比值(B=Rxx/Rx and B-1) Table 2 The ratio of the two relative errors of the actual predicted values of the corrected and not revised prediction samples under different K and different rs′conditions. (B=Rxx/Rx and B-1)

结论：用误差修正公式修正后的预测样本的模型输出值计算得到的样本实际预测值的相对误差, 一定小于未用误差公式修正的模型输出值计算得到的实际预测值的相对误差, 即.

对式(54)讨论如下：

a. K为某一定值时, 两种实际预测值的相对误差比值B随rs′的变化

将式(54)中的B对rs′求偏导数, 化简得

(55)

通常情况下, 0 < K≤1, 0 < rs′ < 1, 其乘积0 < Krs′ < 1, 故式(55)右边大于0, 因此, B是rs′的增函数, 即B随rs′的增大而增大(而其逆B-1则表示修正后的预测精度比不修正的预测精度高的倍数); 反之亦然.同样, 随着rs′的增加, 式(55)右边的导数值减小, 即随着rs′的增大, 2种相对误差的比值B的增加值逐渐减小.

b.当rs′为某一定值时, B随K的变化

将式(54)中的B对K求偏导数, 化简得

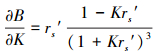
(56)

式(56)与式(55)完全类同, 因其右边大于0, 故B是K的增函数(自然B-1是K的减函数), 即B随K的增大而增大, 但随着K增大, B的增大量逐渐减小.B(或B-1)随rs′和K的变化规律与表 2中的变化规律完全一致.但由于表 2中的rs′的变化范围Δrs′=0.01~1.00, 远大于K值的变化范围ΔK=0.90~1.00.因此, 在rs′为一定值情况下, 不同K值时的比值B(或B-1)差异很小; 在rs′为较大值时, 不同K值时的B(或B-1)几乎完全相同, 见表 2.

结论：修正后的预测样本的实际预测值的相对误差与未作修正的预测样本的实际预测值的相对误差的比值B随相似样本的相似度K和相似样本的相对误差rs′的增大而增大, 而其模型预测精度比不修正的模型预测精度提高的倍数B-1则随K和rs′的增大而逐渐减小, 但B(或B-1)随K的变化远不及随rs′的变化大; 反之亦然.

5 NV-FNN和NV-PPR模型用于某城市SO2浓度预测(Predictions of SO2 concentration in a city based on NV-FNN and NV-PPR models) 5.1 SO2及其影响因子的参照值和规范变换式的设置

某城市SO2浓度值(cy)及其工业耗煤(c1)、人口密度(c2)、交通密度(c3)、饮食服务点(c4)4个影响因子的实际数据, 如表 3所示(刘永等.2004).传统的多种预测模型和方法对此实例预测的效果均不理想, 相对误差较大.依据变换式(1)设计原则及cj0和nj的选择方法, 设置如式(57)所示的变换式, 由式(57)和式(2)计算出各影响因子的规范值xi′及SO2的规范值yi′, 皆如表 3所示.

(57)

式中, c1、c2、c3、、c4和cy的参照值cj0分别设置为：0.00008、0.0004、0.01、0.05和0.00002.

5.2 预测模型训练样本的组成

由于规范变换后的m个因子完全“等效”, 因此, 将规范变换后各个建模样本的第1个、第2个规范因子组成预测模型(NV-FNN或NV-PPR)的第1个训练样本; 再将第2个、第3个规范因子组成预测模型的第2个训练样本; 依次递推, 直至将第m个和第1个规范因子组成预测模型的第m个训练样本.完全类似, 将各建模样本的第1个、第2个、第3个规范因子组成预测模型的第1个训练样本; 再将第2个、第3个、第4个规范因子组成预测模型的第2个训练样本, 依次递推, 直至将第m个、第1个和第2个规范因子组成预测模型的第m个训练样本.两种情况皆是由每个建模样本组成m个训练样本, n个建模样本共组成m×n个训练样本, 分别用于训练NV-FNN和NV-PPR各自的两种简单结构的预测模型.

表 3 某城市SO2浓度的实际值和规范值以及4个影响因子的实际数据和规范值 Table 3 The actual values and standard values of SO2 concentration and 4 influencing factors respectively in a city
5.3 某城市SO2的NV-FNN模型的计算输出

选取样本序号1~25的数据作为建模样本, 样本序号26*~30*的数据作为模型检测样本.分别由表 3中的各建模样本的4个影响因子规范值xi′与相应的SO2规范值yi′, 按上述训练样本的组成法构成4个训练样本, 并将建模样本1~25组成的100个训练样本规范值分别带入NV-FNN(2)(式(6))和NV-FNN(3)(式(7))模型, 用免疫进化算法(倪长健等, 2003).对连接权值whi和vh反复迭代优化.该算法的优点是：不仅可有效避免不成熟收敛, 以更高的精度和较快的速度逼近全局最优解, 而且算法原理简单, 编程简便.当优化目标函数式(13)分别满足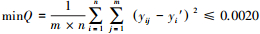和时, 停止迭代, 得到优化好的NV-FNN(2)和NV-FNN(3)模型的权值矩阵whj和vh (h=1, 2; j=1, 2)或whj和vh (h=1, 2; j=1, 2, 3).从而得到NV-FNN(2)和NV-FNN(3)模型的输出式, 分别如式(58)和(59)所示.

(58)
(59)

由式(58)和式(59)计算得到NV-FNN两种结构的建模样本1~25的模型拟合输出值及其拟合相对误差绝对值、检测(预测)样本26*~30*的模型计算输出值, 见表 4.

表 4 某城市SO2两种预测模型输出值及其相对误差绝对值 Table 4 The output values and relative error absolute values of the two class prediction models of SO2 in a city
5.4 某城市SO2的NV-PPR模型的计算输出

与基于NV-FNN预测模型完全类似, 将建模样本1~25组成的100个训练样本规范值分别带入NV-PPR(2)(式(9))和NV-PPR(3)(式(10))模型, 用免疫进化算法对参数矩阵α和β反复迭代优化, 当优化目标函数式(13)分别满足minQ= 和minQ=时, 停止迭代, 分别得到优化好的NV-PPR(2)和NV-PPR(3)模型的参数矩阵元αuj和βu(u=1, 2;j=1, 2或j=1, 2, 3), 从而得到NV-PPR(2)和NV-PPR(3)模型的输出式, 分别如式(60)和(61)所示.

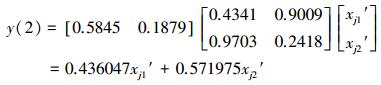
(60)
(61)

由式(60)和式(61)计算得到NV-PPR两种结构模型的建模样本1~25的拟合输出值及其拟合相对误差绝对值、检测样本26*~30*的模型计算输出值, 见表 4.

5.5 两种预测模型的精度检验

由式(28)计算出NV-FNN和NV-PPR两类预测模型的两种不同结构的F统计值分别为F(7.55)、F(7.31)和F(8.03)、F(8.09).模型的F值均大于F0.01(4.18), 表明模型精度检验合格, 预测结果具有可信度.

5.6 预测样本模型输出的误差修正及修正后的SO2浓度预测值

从表 4可知, 与26*号检测样本的NV-FNN和NV-PPR两种模型输出相似的皆为23号建模样本; 与27*号检测样本的NV-FNN两种结构模型输出相似的为12号与19号2个建模样本, 而与27*号检测样本的NV-PPR两种结模型输出相似的为12、14、16、19号4个建模样本; 与28*号检测样本的NV-FNN和NV-PPR两种模型输出相似的皆为12、13、14、16号4个建模样本; 与29*号检测样本的NV-FNN和NV-PPR两种模型输出相似的皆为12号和16号2个建模样本; 与30*号检测样本的NV-FNN和NV-PPR两种模型输出相似的皆为12、16、19、25号4个建模样本, 用式(14)和式(15)进行误差修正后的5个检测样本SO2的NV-FNN和NV-PPR两种模型的两种不同结构预测输出值Yx′, 如表 5所示.再由式(2)和式(57)的逆运算, 计算出两种模型的两种不同结构对5个检测样本的SO2浓度预测值cyi, 亦见表 5.

表 5 5个检测样本的两类预测模型的误差修正后的模型输出值和SO2浓度预测值 Table 5 The model′s output values after error correction and the predictive values of SO2 concentration of two class prediction models for 5 detection samples
5.7 预测结果的分析与比较 5.7.1 多种预测模型的实际预测值的相对误差及比较

5个检测样本的实际预测值与真实(测定)值之间的相对误差Rxz(绝对值)及其平均值和最大相对误差(绝对值)如表 6所示.为了比较, 表 6中亦分别列出了用笔者提出的NV-SVR模型(李祚泳等, 2018)对该5个检测样本的预测的相对误差绝对值及其平均值和最大相对误差绝对值.此外, 表 6中还列出用传统的SVR模型和多个文献中用BP网络(刘永等, 2004)、PPR(彭荔红等, 2002)、模糊识别(熊德琪等, 1993)、组合算子(姜庆华, 2006)及多元回归(姜庆华, 2006)等传统的模型与方法, 对该5个检测样本预测的相对误差绝对值Rxc及其平均值和最大相对误差绝对值.从表 5和表 6可见, 对同一个检测样本, 不仅基于规范变换的同类模型的两种不同结构的预测值及其相对误差几乎完全相同, 而且基于规范变换的3类不同预测模型的预测值及其相对误差也几乎完全相同或彼此相差甚小, 表明模型不但预测精度高, 而且结果稳定; 对多个样本预测的相对误差平均值及最大相对误差也有类似的结果.从表 6还可见, NV-FNN、NV-PPR和NV-SVR 3类预测模型对5个检测样本预测的相对误差绝对值的平均值和最大相对误差绝对值都远小于6种传统模型的预测结果.

表 6 5个检测样本的多种预测模型的预测相对误差的绝对值及其平均值和最大值 Table 6 The relative error absolute values and their average values and the maximal values of multiple prediction models for 5 detection samples
5.7.2 作误差修正和不作误差修正的预测值的理论(估计)相对误差与实际相对误差比较

对每个预测样本, 由误差修正公式修正后的模型输出值yxx′、相似样本的相似度K及相似样本的模型输出值ys′和拟合相对误差rs′, 用式(48)和式(50), 计算得到规范变换的3类预测模型对5个预测样本的用误差修正和不用误差修正的SO2预测值的理论计算(估计)相对误差Rxx和Rx, 如表 7所示.其中, Rx是排除掉相似的异常样本后, 计算得到的相似样本的理论预测相对误差值的均值.表 7中还分别列出未进行误差修正的模型的预测相对误差(Rx)和传统的6种模型的预测相对误差(Rxc)与误差修正的模型预测值的实际相对误差(Rxz)的倍数比.比较表 6和表 7可见：5个预测样本的3类模型预测值的实际相对误差Rxz与用误差修正的理论计算(估计)相对误差Rxx皆非常接近; 而其预测精度比未进行误差修正的理论计算的预测精度提高了数倍到数十倍不等, 见表 7中Rx/Rxz; 与用传统的6种预测模型和方法的预测相对误差Rxc相比, 除30*样本的SVR(3)模型外, 其预测精度也比用传统的6种预测模型和方法的预测精度提高了数倍到数十倍, 亦见表 7中Rxc/Rxz.从而证实了4.3.2节误差修正公式修正后的预测模型的预测精度分析及比较一节中的理论分析和公式推导结果(尤其是式(48)和式(50))的正确性和合理性.从表 7还可以得出：误差修正后的预测值的实际相对误差Rxz与未进行误差修正的预测相对误差Rx相比：当Rx>50%时, Rxz多数会比Rx缩小15-30倍, 即模型预测精度会提高15~30倍不等, 平均提高约25倍; 当20% < Rx≤ 50%时, Rxz多数会缩小10~15倍, 即模型预测精度会提高10~15倍不等, 平均提高约12倍; 当0% < Rx≤20%时, Rxz多数会缩小4~10倍, 即模型预测精度会提高4~10倍不等, 平均提高约5~6倍.由于Rx是预测模型的“外延性(泛化性能)”或“过拟合”的度量指标.可见, 不论模型的“外延性”优劣或“过拟合”程度如何, 用误差修正公式修正后的样本预测值的实际相对误差值Rxz大小相差不大, 多数都能控制在Rxz < 5%范围内, 很少有例外, 即误差修正后的模型的“外延性”变好, “过拟合”程度减弱, 见表 6.因此, 对“外延性”和“过拟合”不同的样本, 用误差修正公式修正后的的预测结果都十分精准、稳定、可靠.基于规范变换与误差修正的两种不同结构的3类预测模型与6种传统的预测模型对5个预测样本预测值的相对误差处于不同误差区间的百分比, 如表 8所示.从表 8可见：前者的相对误差在5%以内占97%, 所有相对误差都在10%以内; 后者的相对误差在5%以内仅占7%, 相对误差在10%以内仅占20%;相对误差在20%以内也只占50%, 而相对误差>20%的却占了50%.

表 7 误差修正模型的Rxz分别与未误差修正模型的Rx和6种传统模型的Rxc的比较 Table 7 Comparisons of Rxz with Rx of non-error correction model and Rxc of six traditional models

表 8 3类误差修正预测模型的Rxz和6种传统预测模型的Rxc处于不同区间所占百分比 Table 8 The percentages of Rxz of three kinds of error correction prediction models and Rxc of 6 traditional prediction models in different intervals
6 模型的分析与比较(Analysis and comparisons of the model) 6.1 样本数量的有限性和样本质量对模型预测精度的影响

虽然从理论上讲, 只要有代表性的训练样本数足够多, 则智能预测模型(如BP、RBF、FNN、PPR、SVR等)都能以任意精度逼近任意函数.不过, 实际问题的样本数总是有限的(即不完备性), 而且, 在有限样本中, 往往还存在若干质量差的样本或异常样本.基于统计理论的学习、模拟来发掘样本共同特性建立的智能预测模型对具有普遍规律的多数样本是适用的和有效的, 但对于质量差的样本或具有特殊规律的异常样本, 则无论是模型的拟合误差还是预测误差都会很大.此外, 某些情况下, 即使模型对训练样本的拟合精度高, 但对于在训练样本集中没有相同或相似样本的那些预测样本, 则预测误差也会很大, 这就是通常所说的“过拟合”.还有, 若模型优化采用的某些优化算法本身存在的局限, 使收敛过程陷入了局部极值, 得不到全局最优, 出现了“欠拟合”, 则模型的拟合和预测误差都会很大.这种由样本的不完备性和样本质量差导致模型预测精度低, 传统预测模型和方法是无法避免的.虽然这些影响因素在NV-FNN、NV-PPR和NV-SVR模型中也同样存在, 但通过采用相似样本误差修正法, 对预测(或检测)样本的模型计算输出值进行修正后, 再计算出预测样本的实际预测值, 可有效消除或至少削弱这些因素对模型预测精度的影响, 此种修正法对提高“过拟合”样本和异常样本的预测精度尤为显著.

6.2 使用的数学方法存在的局限性对模型预测精度的影响

一个理想而又实用的预测模型需满足预测模型结构的复杂性与实际问题的复杂性相匹配.因此, 对训练样本数有限, 而因子数目较多的复杂预测问题, 传统的预测模型通常采用主分量分析法、相关分析法或逐步回归法来减少因子个数(Jubas, 2008), 达到简化模型结构和提高学习效率的目的.但无论用何种方法, 不仅复杂, 而且皆会丢失建模样本部分信息, 致使模型失真, 导致模型预测结果大多精度不高和不同样本的预测的误差差异大(外延性和稳定性差).而基于规范变换的NV-FNN、NV-PPR和NV-SVR预测模型, 仅采用对因子数据进行规范变换的降维处理, 既简化了模型结构, 提高了模型的学习效率; 又因为样本的全部信息都充分得到利用, 无任何信息丢失, 使建立的模型更接近真实, 提高了模型的可靠性和稳定性.

6.3 基于规范变换的预测模型与传统的预测模型的比较

基于规范变换的3种预测模型与传统的3种预测模型的性能比较见表 9.

表 9 规范变换的3种预测模型与传统的3种预测模型的性能比较 Table 9 The performance comparisons between the three prediction models of normal transformation and the traditional three prediction models
7 结论(Conclusions)

1) 对预测变量及其影响因子进行规范变换使预测模型的结构变得简化, 普适、规范和统一, 不仅减小了模型结构的复杂性对预测精度的影响, 而且极大地提高了模型的学习效率和稳定性.

2) 用相似样本的误差修正法对预测样本的模型输出进行误差修正, 可有效消除或削弱样本数量的有限性、样本质量的差异性和算法的局限性等因素对模型预测精度的影响, 能极大地提高模型对预测样本(尤其是“过拟合”样本和异常样本)的预测精度.

3) 规范变换和相似样本的误差修正法相结合用于FNN和PPR预测建模的思想和方法同样可用于BP网络、RBF神经网络、概率神经网络、模糊神经网络、小波神经网络、多元线性回归及灰色GM等传统的预测模型结构的简化和预测效果的改善.

致谢(Acknowledgements): 感谢四川师范大学伍绍贵副教授(博士)对修改英文摘要提供的协助
参考文献
Chen S Y, Ji H L. 2005. Fuzzy optimization neural network approach for ice forecast in the Inner Mongolia reach of the Yellow River[J]. Hydrological Sciences Journal, 50(2): 319–329. DOI:10.1623/hysj.50.2.319.61793
Chen C I. 2008. Application of the novel nonlinear grey Bernoulli model for forecasting unemployment rate[J]. Chaos, Solitons & Fractals, 37(1): 278–287.
Chen S Y, Xue Z C, Li M. 2013. Variable sets principle and method for flood classification[J]. Science China Technological Sciences, 56(9): 2343–2348. DOI:10.1007/s11431-013-5304-4
Comrie A C. 2013. Comparing neural networks and regression models for ozone forecasting[J]. Journal of the Air & Water Mangement Association, 47(6): 653–663.
Diaz Robles L A, Ortega J C, Fu J S, et al. 2008. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco Chile[J]. Atmospheric Environment, 42(35): 8331–8340. DOI:10.1016/j.atmosenv.2008.07.020
笪英云, 汪晓东, 赵永刚, 等. 2015. 基于关联向量机回归的水值预测模型[J]. 环境科学学报, 2015, 35(11): 3730–3735.
Grivas G, Chaloulakon A. 2006. Artificial neural network models for prediction of PM10 hourly concentrations, in the Greater Area of Athens, Greece[J]. Atmospheric Environment, 40(7): 1216–1229. DOI:10.1016/j.atmosenv.2005.10.036
Ghose D K, Panda S S. 2010. Prediction of water table depth in western region, Orissa using BPNN and RBFN neural networks[J]. Journal of Hydrology, 39(4): 296–304.
黄思, 唐晓, 徐文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(1): 56–64.
Jubas I, Makra L, Toth B. 2008. Forecasting of traffic origin NO and NO2 concentrations by support vector machines and neural networks using principal component analysis[J]. Simulation Modelling Prictice and Theory, 16(9): 1488–1502. DOI:10.1016/j.simpat.2008.08.006
姜庆华. 2006. 大气污染预测的参数化组合算子方法[J]. 山东大学学报(理学版), 2006, 41(4): 76–79. DOI:10.3969/j.issn.1671-9352.2006.04.020
金菊良, 魏一鸣, 王文圣. 2009. 基于集对分析的水资源相似预测模型[J]. 水力发电学报, 2009, 28(1): 72–77.
Lange I A, Steel E A. 2007. Using wavelet analysis to detect changes in water temperature regimes at multiples scales:Effects of multi-purpose dams in the Willamette River basin[J]. River Research and Application, 23(4): 351–359. DOI:10.1002/(ISSN)1535-1467
李祚泳, 汪嘉杨, 金相灿, 等. 2007. 基于进化算法的湖泊富营养化投影寻踪回归预测模型[J]. 四川大学学报(工程科学版), 2007, 39(2): 1–8. DOI:10.3969/j.issn.1009-3087.2007.02.001
李祚泳, 徐源蔚, 汪嘉杨, 等. 2015. 基于前向神经网络的广义环境系统评价普适模型[J]. 环境科学学报, 2015, 35(9): 2996–3005.
李祚泳, 汪嘉杨, 徐源蔚. 2018. 基于规范变换与误差修正的回归支持向量机的环境系统预测[J]. 环境科学学报, 2018, 38(3): 1235–1244.
刘永, 郭怀成. 2004. 城市大气污染物浓度预测方法研究[J]. 安全与环境学报, 2004, 4(4): 59–62.
Moazami S, Noori R, Amiri B J, et al. 2016. Reliable prediction of carbon monoxide using development support vector machine[J]. Atmospheric Pollution Research, 7(3): 412–418. DOI:10.1016/j.apr.2015.10.022
Noori R, Barbassi A, Ashrafi K, et al. 2012. Active and online prediction of BOD5 in river systems using reduced-order support vector machine[J]. Environmental Earth Sciences, 67(1): 141–149. DOI:10.1007/s12665-011-1487-9
倪长健, 丁晶, 李祚泳. 2003. 免疫进化算法[J]. 西南交通大学学报, 2003, 38(1): 87–91. DOI:10.3969/j.issn.0258-2724.2003.01.020
Ortiz Garcia E G, Salcedo Sanz S, Perez Bellido A M, et al. 2010. Predic of hourly O3 concentrations using support vector regression algorithms[J]. Atmospheric Environment, 44(35): 4481–4488. DOI:10.1016/j.atmosenv.2010.07.024
Park Y, Cho K H, Park J, et al. 2015. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservois, Korea[J]. Science of the Total Environment, 502: 31–41. DOI:10.1016/j.scitotenv.2014.09.005
Paschalidou A K, Karakitsios S, Kleanthous S, et al. 2011. Forecasting hourly PM10 concentration in Cyprus through artificial neural networks and multiple regression models implications to local environmental management[J]. Environmental Science and Pollution Research, 18(2): 316–327. DOI:10.1007/s11356-010-0375-2
彭荔红, 李祚泳, 郑文教, 等. 2002. 环境污染的投影寻踪回归预测模型[J]. 厦门大学学报(自然科学版), 2002, 41(1): 79–83. DOI:10.3321/j.issn:0438-0479.2002.01.018
Qi X N, Liu Z G, Li D D. 2008. Prediction of the performation of a shower cooling tower based on projection pursuit regression[J]. Application Thermal Engineering, 28(10): 1031–1038.
Shaban K B, Kadri A, Rezk E, et al. 2016. Urban air pollution monitoring system with forecasting models[J]. IEEE Sensors Journal, 16(8): 2598–2606. DOI:10.1109/JSEN.2016.2514378
孙宝磊, 孙蒿, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 2017, 37(5): 1864–1871.
Wang X G, Tang Z, Tamura H, et al. 2004. An improved bad - propagation algorithm to avoid the local minima problem[J]. Neuro Computing, 56(1): 455–460.
王保良, 范昊, 冀海峰, 等. 2016. 基于分段线性表示的最近邻的水质预测方法[J]. 环境工程学报, 2016, 10(2): 1005–1009.
肖鸣, 李卫明, 刘德富, 等. 2017. 基于多重优化灰色模型的三峡库区香溪河支流回水区水华变化趋势预测研究[J]. 环境科学学报, 2017, 37(3): 1153–1161.
熊德琪, 陈守煜. 1993. 城市大气污染物浓度预测模糊识别理论与模型[J]. 环境科学学报, 1993, 13(4): 482–490.
杨云, 付彦丽. 2016. 关于空气中PM2.5质量浓度预测研究[J]. 计算机仿真, 2016, 33(3): 413–418. DOI:10.3969/j.issn.1006-9348.2016.03.092
邹志红, 王乐娟. 2009. 湖泊富营养化趋势的灰色马尔柯夫预测[J]. 环境科学学报, 2009, 29(2): 427–432. DOI:10.3321/j.issn:0253-2468.2009.02.029
郑彤, 陈春云编. 2003. 环境系统数学模型[M]. 北京: 化学工业出版社: 31.