自然界和人类社会都是不断发展和变化的, 为了人类能更好地生存和发展, 我们不仅要了解环境的过去和现状, 还要能预见环境的未来.因此, 人们提出了多种可用于环境系统预测的机理性模型和非机理性模型.非机理性预测模型因不涉及较复杂的产生机理、相对简单、应用方便而常被采用.非机理性预测模型主要有基于概率统计原理的多元线性回归(Giorgio et al., 2006; 黄思等, 2015)、分段线性分析(Chen et al., 2013)、时序分析(Diaz Robles et al., 2008; Thoe et al., 2012)、门限回归(廖杰等, 2006)、最近邻估计(蒋尚明等, 2013; 王保良等, 2016)等各种环境统计预测模型;有基于模糊分析(Chen et al., 2005)、灰色分析(Chen 2008; 代伟等, 2016)、集对分析(徐源蔚等, 2015)等不确定性分析的环境预测模型;还有基于神经网络(Palani et al., 2008; Paschalidou et al., 2011; Gazzaz et al., 2012; Li et al., 2014; 张旭东等, 2016; 孙宝磊等, 2017)、投影寻踪(PP)(Xiaoni et al., 2008; 崔东文等, 2016)和支持向量机(SVR)(Liu et al., 2013; Moazami et al., 2016; Shaban et al., 2016)等环境系统智能预测模型或改进的智能预测模型(笪英云等, 2015;秦喜文等, 2016).
上述传统的预测模型各有其特点, 但其共同不足之处是:①当影响因子较多而又复杂(比如数据非线性、非正态、波动大)情况下, 不仅模型结构设计复杂, 计算工作量大, 计算效率低, 收敛速度慢;而且因为需要优化的参数多, 在参数优化调试过程中, 需要兼顾具有不同特性的众多因子, 以满足不同预测模型制定的目标函数式的精度要求.因此, 不论是智能预测模型, 还是统计预测模型, 即使训练时间长, 模型也很难达到指定的精度要求.②虽然从理论上讲, 只要有代表性的训练样本数足够多, 模型结构又与问题相匹配, 多数预测模型(比如智能预测模型)都能以任意精度逼近任意函数.不过, 对于实际问题, 样本数总是有限的, 而且代表性也是不完全的.因此, 对高维、非线性预测问题, 传统预测模型的预测效果也难以满足实际需要.为此, 传统的预测模型只能的选择是:要么增加训练样本个数, 以满足模型的复杂结构;要么减少因子个数, 以简化模型结构.对于实际问题, 增加训练样本个数往往是不现实的;为了简化预测模型结构, 传统的统计预测建模或采用主分量分析法提取少数几个主成分作为预测建模的因子(Sousa et al., 2007; 李嵩等, 2015), 或用相关系数法剔除不重要的因子(田静毅等, 2015), 或用相似性准则选择对预测变量有显著作用的因子(Liu et al., 2015).但无论用何种减少因子个数的方法来简化模型结构, 皆会丢失样本部分信息, 致使模型部分失真.这也许就是传统的预测模型预测结果大多不理想(精度不高)和对不同样本(尤其对异常样本)预测的误差差异很大(稳定性差)的原因之一.因此, 为了建立收敛速度较快, 而又有较高预测精度的预测模型, 不仅需要在不损失样本信息的情况下简化模型结构, 而且还必须消除或削弱因样本数有限(不完备)和样本的代表性不全而对模型预测精度的影响.
从实用角度出发, 一元线性回归预测模型应是最简单的预测模型, 但传统的一元线性回归(ULR)预测模型只适用于单因子线性问题预测, 不能用于多因子、非线性问题预测.不过, 文献(李祚泳等, 2019)依据误差理论, 推导得出:不论变量的原始数据具有何种分布特征及呈现什么样变化规律, 总可以借助于一个有可调参数的幂函数变换式和对数变换式组成的规范变换式, 将其规范化、降维化和线性化, 若再结合预测样本模型输出的误差修正公式, 就能大幅提高模型预测精度, 与采用预测模型的具体形式无关.因此, 将基于规范变换与误差修正结合用于一元线性回归(Univariate Linear Regression of normalized variable, NV-ULR)预测模型也应该是适合的.这样的模型不仅能简化模型结构, 而且还能极大地提高模型的预测精度.
2 预测变量及其影响因子的规范变换式(Standard transformation formula of predictive variables and their influencing factors)对多个影响因子的预测建模, 虽然不同因子的量纲、单位、数值大小和变化特性(线性或非线性、正态或非正态、独立或相关、正向或逆向)不尽相同, 但正如文献(李祚泳等, 2018)所指出的:若构建如式(1)所示的正幂函数变换式(幂指数b>0)和式(2)所示的对数变换式相结合的规范变化式, 对环境系统预测变量及其各影响因子的原始数据进行规范变换.由于满足一定变换要求的正幂函数变换式(1)能使所有样本各因子变换后的幂函数数据特性和变化规律大体协调一致, 数值大小差异减小;再通过式(2)对各因子的幂函数值进行对数变换, 对数变换不仅能使变换后的样本的不同因子规范值差异进一步减小, 而且对数变换还可将幂函数值线性化.为了使规范后的各因子可以视作一个“等效”线性规范因子, 规范变换还需满足变换后的预测变量及各因子的最小规范值xjm′(或yjm′)和最大规范值xjM′(或yjM′)分别被限定在各自的较小区间内.两个区间各自的限定范围和两个区间之间的间隔距离都不能太大或太小.若太大, 将规范变换后的所有因子视为同一个“等效”规范因子就不能成立;若太小, 某些情况下又可能使有的因子参照值cj0的选取和调试变得困难.此外, 考虑到这两个区间限定范围及两个区间之间的间隔距离最好分别与基于规范变换的评价模型的最低一级评价标准和最高一级评价标准的指标规范值区间范围相一致, 最终选择[0.10, 0.24]和[0.40, 0.55]分别作为最小规范值和最大规范值的限定区间.可见, 规范变换的目的为:借助规范变换, 将任意数据分布的高维、非线性复杂预测建模问题转化为对“等效”规范因子的简单一元线性回归的预测建模问题, 从而极大的简化模型结构, 使计算变得十分简单.

|
(1) |
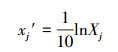
|
(2) |
式中, cj为因子或预测变量实际值;cj0为设置的因子或预测变量的参照值;cjb为设定的因子或预测变量的阈值;Xj和xj′分别为因子或预测变量的变换值和规范值;k代表全体样本个数;nj为如式(3)所示的因子或预测变量的幂指数.式(1)右边1~4行适用于正向类因子或预测变量的变换;5~8行适用于逆向类因子或预测变量的变换.

|
(3) |
式中, tj为因子或预测量实际值的最大值与最小值之比值, 具体如式(4)所示.式(1)~(4)中的参数cjb、nj、cj0和tj的确定过程详见文献(李祚泳等, 2019).

|
(4) |
为使预测样本尤其是异常预测样本(或检测样本)的预测(或检测)值更接近实际值, 多数情况下需用式(5)和式(6)所示的误差修正计算公式, 对预测(或检测)样本的模型输出值进行误差修正, 然后将修正后的预测样本的模型输出值再代入规范变换式(1)和(2), 进行逆运算, 计算出样本实际预测值.

|
(5) |

|
(6) |
式中, yx′和yxx′分别为预测(或检测)样本修正前和修正后的模型计算输出值;rx′为计算得到预测(或检测)样本模型输出的估计相对误差的绝对值;ys′和rs′分别为在建模样本集中, 与预测(或检测)样本的模型输出值yx′最接近的一个或多个相似样本的模型拟合输出值及拟合相对误差的绝对值.误差修正的基本思想和误差修正公式的具体使用说明详见文献(李祚泳等, 2019).
4 NV-ULR预测模型的建模理论依据及建模过程(Theoretical basis and modeling process of NV-ULR prediction mdel)依据误差理论, 对基于因子规范变换与误差修正公式相结合的任何类型的预测模型的预测精度, 用数学分析方法从定量角度获得的结果表明:其模型预测精度比不用误差修正公式修正的模型预测精度或传统的预测模型的预测精度皆能提高数倍到数十倍不等, 与采用预测模型的具体形式无关.其严格的数学推导、论证过程和结果详见文献(李祚泳等, 2019).因此, 这一结论无疑对基于规范变换降维与误差修正相结合的一元线性回归预测模型也是成立的.NV-ULR模型的预测建模过程如图 1所示.
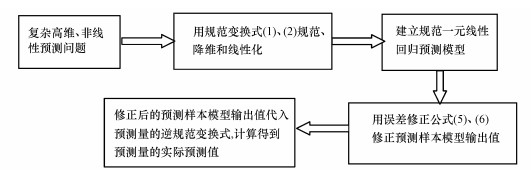 |
| 图 1 NV-ULR模型的预测建模过程示意图 Fig. 1 A schematic diagram of the predictive modeling process of the NV-ULR model |
结合环境系统的3个实例, 说明规范变换与误差修正相结合, 分别用于多因子和时序变量的一元线性回归预测的实现过程.
5.1 某市SO2浓度的一元线性回归预测模型 5.1.1 SO2及其影响因子的参照值和规范变换式的设置某城市SO2浓度(Cy)及其工业耗煤(C1)、人口密度(C2)、交通密度(C3)、饮食服务点(C4)4个影响因子的监测数据如表 1所示(刘永等, 2004).传统的多种预测模型和方法对此实例预测结果的相对误差皆较大.为了与多种传统的预测模型和方法的预测结果相比较, 本文采用规范变换降维与误差修正相结合建立一元线性回归预测模型.依据cj0和nj的设计原则和方法及变换式(1), 设置如式(7)所示的变换式, 由式(7)和式(2)计算出各影响因子的规范值xi′及SO2的规范值yi′, 具体如表 1所示.
| 表 1 某城市SO2浓度及4个影响因子的监测数据和规范值 Table 1 The monitoring data and standard values of SO2 concentration and 4 influencing factors in a city |

|
(7) |
式中, 因子C1、C2、C3、C4和SO2 (Cy)的参照值cj0分别设置为0.8 t·km-2、4人·km-2、0.5辆·km-2、0.05个· km-2和0.00002 mg·m-3.
5.1.2 SO2浓度规范值的一元线性回归预测模型选取表 1中序号1~25的数据作为建模样本, 序号26*~30*的数据作为模型检验样本.由于规范变换后的4个因子皆等效于同一个规范因子, 因而具有这4个因子、n个样本的预测建模可简化为只对一个等效规范因子、N=m×n个样本的一元线性回归预测模型, 用最小二乘法优化建立的一元线性回归预测模型具体为:
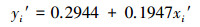
|
(8) |
分别将表 1中各样本的4个影响因子规范值xi1′、xi2′、xi3′和xi4′代入式(8)计算, 并求平均, 得到前25个SO2建模样本(序号1~25)的一元线性回归模型拟合输出值yi′及拟合相对误差绝对值ri′, 具体如表 2所示;类似, 计算得到后5个SO2预测(检测)样本(序号26*~30*)的一元线性回归模型预测输出值yx′, 具体见表 2.
| 表 2 某市SO2浓度规范值的一元线性回归预测模型的输出值及拟合相对误差 Table 2 Output values and fitting relative error of univariate linear regression prediction model for SO2 concentration standard value in a city |
由表 2可知, 与序号26*的样本模型输出相似的建模样本有序号8、10、23和24共4个建模样本;与序号27*的样本模型输出相似的有序号7、12和16共3个建模样本;与序号28*的样本模型输出相似的有序号12、13和16共3个建模样本;与序号29*的样本模型输出相似的有序号7、12和16共3个建模样本;与序号30*的样本模型输出相似的有序号7、13和16共3个建模样本.用式(5)和式(6)修正后5个SO2预测样本(26*~30*)的一元线性回归模型预测输出值yx′分别为0.3618、0.3842、0.4110、0.4136和0.4249.再由式(2)和式(7)的逆运算式cy=cj0e20y′x, 计算得到5个预测样本的SO2浓度预测值cy分别为0.0278、0.044、0.074、0.0783和0.098 mg·m-3.5个预测样本的SO2浓度的一元线性回归模型预测值的相对误差绝对值及其平均值和最大值如表 3所示.表 3中还列出研究者(李祚泳等, 2018; 2019)用基于规范变换与误差修正相结合的NV-FNN、NV-PPR、NV-SVR 3种预测模型及其他文献用传统的BP网络(刘永等, 2004)、PPR(彭荔红等, 2002)、模糊识别(熊德琪等, 1993)、组合算子(姜庆华, 2006)及多元回归(姜庆华, 2006)等多种模型对后5个预测样本预测结果的相对误差绝对值的平均值和最大的相对误差绝对值.从表 3可以看出, 基于规范变换的一元线性回归模型(NV-ULR)对5个预测样本预测结果的相对误差绝对值的平均值和最大的相对误差绝对值均远小于传统的5种预测模型预测的相应相对误差, 也略小于基于规范变换的两种不同结构的3种预测模型的相应误差.
| 表 3 多种预测模型预测的5个检测样本的相对误差绝对值及其平均值和最大值 Table 3 Absolute relative error values, mean value and maximum value of five detection samples predicted by multiple prediction models |
1981—1999年南昌市城市降水酸度pH(Cy)及其SO2(C1)、NOx(C2)、TSP(C3)、降尘(C4)4个影响因子的监测数据(cy, cj)如表 4所示(汤丽妮等, 2003).依据cj0、cb和nj的设计原则和方法及变换式(1), 设置如式(9)所示的变换式, 由式(9)和式(2)计算出各影响因子的规范值xij′及降水酸度pH的规范值yi′(表 4).
| 表 4 南昌市的降水酸度及其影响因子的监测数据和规范值(1981—1999年) Table 4 Monitoring data and standard values of precipitation acidity and its influencing factors in Nanchang (1981—1999) |

|
(9) |
式中, C1、C2、C3、C4和Cy的参照值cj0分别设置为0.32、0.2、1.5、2.5 mg·m-3和0.03;Cy的阈值cb为4.
5.2.2 降水酸度pH规范值的一元线性回归预测模型选取1981—1995年的数据作为建模样本, 1996—1999年的数据作为模型检验样本.预测建模过程与实例1的SO2浓度的一元回归预测建模过程完全类似, 从而建立基于降水酸度pH规范值的一元线性回归预测模型为:
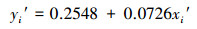
|
(10) |
分别将表 4中各样本的4个影响因子规范值xi1′、xi2′、xi3′和xi4′代入式(10)计算, 并求平均, 得到前15个样本(1981—1995年) pH的一元线性回归模型拟合输出规范值yi′及拟合相对误差绝对值ri′(表 5);类似, 计算得到后4个预测样本(序号1996*—1999*年)pH的一元线性回归模型预测输出规范值yx′(表 5).
| 表 5 南昌市pH规范值的一元线性回归预测模型的输出值及拟合相对误差 Table 5 Output values and fitting relative error of univariate linear regression prediction model of pH norm value in Nanchang City |
由表 5可见, 与1996*年样本模型输出相似的有1992和1993年2个建模样本;与1997*年样本模型输出相似的只有1992年1个建模样本;与1998*年样本模型输出相似的有1986、1987年2个建模样本;与1999*年样本模型输出相似的有1986年1个建模样本.用式(5)和式(6)修正后4个预测样本的pH规范值的一元线性回归模型预测输出值yx′分别为0.2915、0.2773、0.2935和0.3038;再由式(2)和式(9)的逆运算式cy=cb+cj0e10y′x, 计算出4个预测样本的pH的一元线性回归模型预测值cy分别为4.56、4.48、4.57、4.63. 4个预测样本的pH的一元线性回归模型预测值的相对误差绝对值rx及相对误差绝对值的平均值和最大值见表 6.表 6中还列出研究者(李祚泳等, 2018; 2019)用基于规范变换与误差修正相结合的NV-FNN、NV-PPR、NV-SVR模型, 以及其他文献用基于集对分析的相似预测模型(徐源蔚等, 2015)、传统的时序Holt′S模型、多元线性回归模型、BP网络模型(毛端谦等, 2001)和GA-BP网络模型(汤丽妮等, 2003)等多种模型对4个预测样本pH预测值的相对误差绝对值及其平均值和最大值.从表 6可以看出, NV-ULR模型对4个预测样本预测结果的相对误差绝对值的平均值和最大的相对误差绝对值均小于其他5种传统的预测模型的相应误差, 而与基于规范变换的两种不同结构的3种预测模型的相应误差十分接近.
| 表 6 多种预测模型预测的4个检测样本的相对误差绝对值及其平均值和最大值 Table 6 Absolute relative error values, mean value and maximum value of four detection samples predicted by multiple prediction models |
伦河孝感段2008年8月—2011年12月每2个月采集1次数据,共21个月的CODMn时间序列数据如表 7第2列所示(崔雪梅, 2013).依据cj0、cb和nj的设计原则和方法, 设置如式(11)所示的变换式, 由式(11)和式(2)计算出CODMn时间序列的规范值xi′如表 7第3列所示.取t时刻前的最近邻时刻数k=3, 则从第4个样本(第4周)开始, 由每个样本的前3个最近邻样本的规范值构成的时间序列如表 7第4~6列所示.
| 表 7 2008年8月—2011年12月伦河孝感段的CODMn监测数据ct及其规范值xt′ Table 7 CODMn monitoring data ct and its standard values xt′in Xiaogan section of Lun River (2008-8—2011-12) |

|
(11) |
式中, 参照值cj0= 0.5 mg·L-1.
5.3.2 CODMn时序规范值的一元线性回归预测模型分别选取表 7中第4~18个样本和第19*~21*个样本的时间序列数据xt′作为建模样本和预测样本.建立CODMn的规范值的一元线性回归预测模型(NV-ULR), 具体如式(12)所示.
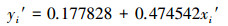
|
(12) |
分别将表 7中样本的3个影响因子规范值xt-1′、xt-2′和xt-3′代入式(12)计算, 并求平均, 得到前15个样本(序号4~18)的CODMn的一元线性回归模型拟合输出规范值yi′及拟合相对误差绝对值ri′(表 8);类似, 计算得到后3个预测样本(序号19*~21*)的CODMn的一元线性回归模型输出规范值yx′(表 8).
| 表 8 伦河孝感段CODMn规范值的一元线性回归预测模型的输出值及拟合相对误差 Table 8 Output values and fitting relative error of univariate linear regression prediction model for CODMn concentration standard value in Xiaogan section of Lun River |
由表 8可知, 与19*号样本模型输出相似的只有18号1个建模样本, 用式(5)和式(6)修正后19*号预测样本的CODMn的一元线性回归模型预测输出值yx′为0.3416;而20*号和21*号预测样本都没有相似样本, 因此, 模型预测输出值yx′不用修正, 即分别为0.3404和0.3394.再由式(2)和式(11)逆运算式cy=cj0e5y′x, 计算得到3个预测样本的CODMn的一元线性回归模型预测值cy分别为2.76、2.74和2.73 mg·L-1.3个预测样本的CODMn的NV-ULR模型预测值的相对误差绝对值rx及相对误差绝对值的平均值和最大值见表 9.表 9中还列出研究者(李祚泳等, 2018; 2019)用NV-FNN、NV-PPR、NV-SVR等模型和文献(崔雪梅等, 2013)用GA-LM-BP模型对3个预测样本的CODMn预测值的相对误差绝对值及其平均值和最大值.从表 9可以看出, NV-ULR模型对3个预测样本预测结果的相对误差绝对值的平均值和最大的相对误差绝对值均远小于GA-LM-BP网络预测模型的相应误差, 也略小于基于规范变换的两种不同结构的3种预测模型的相应误差.
| 表 9 3个检测样本的多种预测模型的相对误差绝对值及其平均值和最大值 Table 9 Absolute relative error values, mean value and maximum value of three detection samples predicted by multiple prediction models |
NV-ULR与NV-FNN、NV-PPR及NV-SVR 4种预测模型用于同一个预测问题, 只要都依据同一个规范变换式变换, 并用相似样本误差修正公式修正后的4种预测模型, 无论是对单个样本预测的相对误差绝对值, 还是对多个样本预测的相对误差绝对值的平均值或最大值都相差甚小, 而且预测值都与实际值十分接近, 很少有例外(表 3、6和9), 表明4种预测模型均是稳定、可靠的.因此, 对一个实际问题, 采用4种预测模型中的任意一种预测均是有效、可行的.不过若为了增加预测结果可靠性, 可同时采用几种模型预测, 以便相互印证.而NV-ULR预测模型比其他3种预测模型更简便, 因而更具有实用性.
6.2 NV-ULR预测模型与传统的预测模型的比较NV-ULR首先通过选择和调整幂函数变换式(1)中的参数(幂指数nj和参照值cj0, 有时还有阈值cb), 在将逆向因子转化为正向因子的同时, 用nj=2的拉伸变换, 使数据波动性小的变量(包括影响因子变量cj和预测变量cy)的波动性增强;用nj=0.5的压缩变换, 使波动性大的变量的波动性减弱;而用nj=1的线性变换使变量的特性保持不变;可见, 变换式(1)使变量之间的波动性差异变小, 趋于一致.因此, 变换式(1)能将具有任意分布特征和复杂变化规律的预测变量及其各影响因子的数据, 映射(转换)为分布特征和变化规律大体相似和协调一致的正幂函数表示形式, 从而具有普适、规范性;其次, 再用对数变换式(2)将变量线性化, 而且要求线性化后变量的最小规范值和最大规范值分别被限定在一个较小范围内, 使因子变量之间的差异进一步减小.因此, 借助幂函数变换式(1)的规范化和对数变换式(2)的线性化, 使规范变换后的每个影响因子皆可视为“等效”于某一个线性规范因子, 将预测变量受m个因子影响的复杂问题, 转化为预测变量仅受1个“等效”线性规范因子的m次影响的一元问题, m个因子的n个样本的复杂建模问题也就转化为只需1个“等效”线性规范因子的m×n个样本的简单一元线性回归建模问题, 极大地减少了因子数目(将m维降为1维), 达到预测模型结构简化的目的;传统的数据变换式(比如极差归一化和均值-方差标准化)各因子之间是彼此独立无关的变换, 变换后不同因子的数据分布特性和变化规律也不会相同, 因此, 变换后的各因子不能用一个“等效”因子代替, 也就不能简化模型结构.这正是规范变换与传统数据变换的区别所在.
线性化是解决非线性、高维复杂问题的一种常用手段.不过, 将非线性问题线性化, 一定程度上削弱了原数据的波动性, 增强了平滑性.因此, 在用对数变换式(2)进行线性变换后, 虽然可以用简单的一元线性回归建模, 但确实会使原数据的波动性减弱, 因而在低维空间建立的一元线性回归模型不可能精确反映原高维空间数据的非线性变化特性.因此, 若直接用一元线性回归模型计算得到的预测样本的模型输出值, 代入预测量的逆规范变换式进行运算, 得到的预测样本实际预测值与样本真实值可能相差较大.为提高预测精确度, 依据相似原因产生相似结果的原理, 本文提出:先将计算得到的预测样本的模型输出值与最接近的建模拟合样本的模型输出值进行比较, 并用一个相似样本的误差修正公式, 对预测样本的模型输出值修正后, 再代入预测量的规范变换式进行逆运算.这样使得原空间非线性复杂数据的波动性又得到恢复和重现, 从而可以得到与预测样本真实值非常接近的样本预测值, 提高了模型的预测稳定性和预测精确度.对高维、非线性问题, 传统的预测模型结构复杂, 计算量大, 预测的稳定性和准确度差.为了提高预测精确度, 常采用对拟合样本的残差(拟合误差)再建模, 用优化得到的残差模型参数来修正原预测模型参数, 以提高模型的拟合精度和预测精度.但往往事与愿违, 因为这很可能由“欠拟合”转为出现“过拟合”.传统的一元线性回归预测模型(ULR)只能用于单个影响因子的线性问题预测, 而NV-ULR预测模型则对单因子、多因子、线性、非线性和时序问题都同样适用.这又是本文预测模型与传统预测模型的显著不同之处.
本方法的优势在于不管样本空间是高维还是低维, 不论样本变量之间是简单的线性关系或是复杂的非线性关系, 也不论样本变量的变化规律是趋势性或波动性、平稳或剧烈、快变或缓变, 通过选择适当的参数nj、cj0和cb, 都可以用幂函数和对数函数结合的规范变换式进行映射变换, 使其规范化、降维化、线性化.如果原始数据本身就是线性的, 则取nj=1, 用式(1)变换后仍是线性的, 若原始数据是非线性的, 则取nj=2或nj=0.5, 用式(1)变换后非线性程度弱化, 变得近似线性.因此规范变换具有普适性.
6.3 NV-ULR模型对异常样本的预测若预测样本是“异常”样本(指与正常样本的影响因子值相同或相近而预测量值差异很大的样本, 类似遥感图象识别中的“同谱异物”), 但在训练样本集中, 不仅没有与该输出相似的“异常”拟合样本(指拟合误差很大), 而且也没有任何非相似的“异常”拟合样本, 则因不能用误差修正公式对该异常预测样本模型输出值进行误差修正, 而使预测结果误差较大;但若训练样本集中, 有与该“异常”预测样本模型输出值相似的“异常”拟合样本, 或者虽然没有与该“异常”预测样本模型输出值相似的“异常”拟合样本, 但存在非相似的“异常”拟合样本, 则皆可用相似的‘异常“拟合样本(或非相似的”异常“拟合样本)的误差进行误差修正, 往往还是可以得到较好的预测结果.
7 结论(Conclusions)1) 理论分析和对多个学科、领域众多实例验证表明, 只要将规范变换和相似样本误差修正法相结合用于任何预测模型, 其稳定性和预测精度都会获得极大的提高, 与具体采用何种预测模型无关.
2) 对任意多因子、非线性复杂的预测建模或时间序列的预测建模, 只要将规范变换与误差修正法相结合, 都可以简化为简单的一元线性回归预测模型, 使任何预测模型变得普适、规范、统一和极大的简化, 而且还能大幅度提高模型的预测精度, 具有实用性.
3) 规范变换与误差修正相结合的一元线性回归预测建模思想和方法具有普适性, 因而对其他学科、领域的预测问题也同样适用.
致谢(Acknowledgements): 感谢四川师范大学伍绍贵副教授(博士)对修改英文摘要提供的协助.
Chen C I. 2008. Application of the novel nonlinear grey Bernoulli model for forecasting unemployment rate[J]. Chaos, Solitons & Fractals, 37(1): 278–287.
|
Chen S Y, Ji H L. 2005. Fuzzy optimization neural network approach for ice forecast in the Inner Mongolia reach of the Yellow River[J]. Hydrological Sciences Journal, 50(2): 319–329.
DOI:10.1623/hysj.50.2.319.61793
|
Chen S Y, Xue Z C, Li M. 2013. Variable sets principle and method for flood classification[J]. Science China Technological Sciences, 56(9): 2343–2348.
DOI:10.1007/s11431-013-5304-4
|
崔东文, 金波. 2016. 鸟群算法-投影寻踪回归模型在多元变量年径流预测中的应用[J]. 人民珠江, 2016, 37(11): 26–30.
DOI:10.3969/j.issn.1001-9235.2016.11.006 |
崔雪梅. 2013. 基于灰色GA-LM-BP模型的CODMn预测[J]. 水利水电科技进展, 2013, 33(5): 38–41.
|
Diaz Robles L A, Ortega J C, Fu J S, et al. 2008. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco Chile[J]. Atmospheric Environment, 42(35): 8331–8340.
DOI:10.1016/j.atmosenv.2008.07.020
|
笪英云, 汪晓东, 赵永刚, 等. 2015. 基于关联向量机回归的水质预测模型[J]. 环境科学学报, 2015, 35(11): 3730–3735.
|
代伟, 李克国, 曲东. 2016. 等维灰色递补动态模型在秦皇岛市大气污染预测中的应用[J]. 安徽农业科学, 2016, 39(18): 11026–11027.
|
Gazzaz N M, Yusoff M K, Aris A Z, et al. 2012. Artificial neural network modeling of the water quality index for Kinta River (Malaysis) using water quality variables as predictors[J]. Marine Pollution Bulletin, 64(11): 2409–2420.
DOI:10.1016/j.marpolbul.2012.08.005
|
Giorgio E M, Giovanna R M. 2006. A mixed model-assisted regression estimator that uses variables employed at the design stage[J]. Statistical Methods and Applications, 15(2): 139–149.
DOI:10.1007/s10260-006-0006-8
|
黄思, 唐晓, 徐文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 2015, 35(21): 56–64.
|
蒋尚明, 金菊良, 袁先江, 等. 2013. 基于近邻估计的年径流预测动态联系数回归模型[J]. 水利水电技术, 2013, 44(7): 5–9.
DOI:10.3969/j.issn.1000-0860.2013.07.002 |
姜庆华. 2006. 大气污染预测的参数化组合算子方法[J]. 山东大学学报(理学版), 2006, 41(4): 76–79.
DOI:10.3969/j.issn.1671-9352.2006.04.020 |
Li P H, Li Y G, Xiong Q Y, et al. 2014. Application of a hybrid quantized Elman neural network in short-term load forecasting[J]. International Journal of Electrical Power & Energy Systems, 55: 749–759.
|
Liu S Y, Tai H J, Ding Q S, et al. 2013. A hybrid approach of support vector regression with genetic algorithm optimization for aquaculture water quality prediction[J]. Mathematical and Computer Modeling, 58(4/3): 458–465.
|
Liu Y H, Zhu Q, Yao D, et al. 2015. Forecasting urban air quality via a back-propagation neural network and a selection sample rule[J]. Atmosphere, 6(7): 891–907.
DOI:10.3390/atmos6070891
|
廖杰, 王文圣, 李跃清, 等. 2006. 支持向量机及其在径流预测中的应用[J]. 四川大学学报(工程科学版), 2006, 38(6): 24–28.
DOI:10.3969/j.issn.1009-3087.2006.06.005 |
刘永, 郭怀成. 2004. 城市大气污染物浓度预测方法研究[J]. 安全与环境学报, 2004, 4(4): 59–62.
|
李祚泳, 汪嘉杨, 徐源蔚. 2018. 基于规范变换与误差修正的回归支持向量机的环境系统预测[J]. 环境科学学报, 2018, 38(3): 1235–1244.
|
李祚泳, 汪嘉杨, 徐源蔚. 2019. 规范变换与误差修正结合的环境系统的前向网络和投影寻踪预测模型[J]. 环境科学学报, 2019, 39(6): 2053–2070.
|
李嵩, 王翼, 张丹闯, 等. 2015. 大气PM2.5污染指数预测优化模型仿真分析[J]. 计算机仿真, 2015, 32(12): 400–407.
DOI:10.3969/j.issn.1006-9348.2015.12.086 |
Moazami S, Noori R, Amiri B J, et al. 2016. Reliable prediction of carbon monoxide using development support vector machine[J]. Atmospheric Pollution Research, 7(3): 412–418.
DOI:10.1016/j.apr.2015.10.022
|
毛端谦, 刘春燕, 廖富强. 2001. BP神经网络在降水酸度预测中的应用[J]. 环境与开发, 2001, 16(3): 35–36.
|
Palani S, Liong S Y, Tkalich P. 2008. An ANN application for water quality forecasting[J]. Marine Pollution Bulletin, 56(9): 1586–1597.
DOI:10.1016/j.marpolbul.2008.05.021
|
Paschalidou A K, Karakitsios S, Kleanthous S, et al. 2011. Forecasting hourly PM10 concentration in Cyprus through artificial neural networks and multiple regression models implications to local environmental management[J]. Environmental Science and Pollution Research, 18(2): 316–327.
DOI:10.1007/s11356-010-0375-2
|
彭荔红, 李祚泳, 郑文教, 等. 2002. 环境污染的投影寻踪回归预测模型[J]. 厦门大学学报(自然科学版), 2002, 41(1): 79–83.
DOI:10.3321/j.issn:0438-0479.2002.01.018 |
Qi X N, Liu Z G, Li D D. 2008. Prediction of the preformation of a shower cooling tower based on projection pursuit regression[J]. Application Thermal Engineering, 28(10): 1031–1038.
|
秦喜文, 刘媛媛, 王新民, 等. 2016. 基于整体经验模态分解和支持向量机回归的北京市PM2.5预测[J]. 吉林大学学报(地球科学版), 2016, 46(2): 563–568.
|
Shaban K B, Kadri A, Rezk E, et al. 2016. Urban air pollution monitoring system with forecasting models[J]. IEEE Sensors Journal, 16(8): 2598–2606.
DOI:10.1109/JSEN.2016.2514378
|
Sousa S I V, Martins F G, Alvim Ferraz M C M, et al. 2007. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations[J]. Environmental Modelling & Software, 22(1): 97–103.
|
孙宝磊, 孙蒿, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 2017, 37(5): 1864–1871.
|
汤丽妮, 李祚泳. 2003. 基于遗传算法的人工神经网络在降水酸度预测中的应用[J]. 重庆环境科学, 2003, 25(9): 59–61.
DOI:10.3969/j.issn.1674-2842.2003.09.019 |
Thoe W, Wong S H C, Choo K W, et al. 2012. Daily prediction of marine beach water quality in Hong Kong[J]. Journal of Hydro-environment Research, 6(3): 164–180.
DOI:10.1016/j.jher.2012.05.003
|
田静毅, 范泽宣, 孙丽华. 2015. 基于BP神经网络的空气质量预测与分析[J]. 辽宁科技大学学报, 2015, 38(2): 131–136.
|
王保良, 范昊, 冀海峰, 等. 2016. 基于分段线性表示的最近邻的水质预测方法[J]. 环境工程学报, 2016, 10(2): 1005–1009.
|
熊德琪, 陈守煜. 1993. 城市大气污染物浓度预测模糊识别理论与模型[J]. 环境科学学报, 1993, 13(4): 482–490.
|
徐源蔚, 李祚泳, 汪嘉杨. 2015. 基于集对分析的降水酸度及水质相似预测模型研究[J]. 环境污染与防治, 2015, 37(2): 59–62, 88.
|
张旭东, 高茂亭. 2016. 基于IGA-BP网络的水质预测方法[J]. 环境工程学报, 2016, 10(3): 1566–1571.
|
 2019, Vol. 39
2019, Vol. 39


