自改革开放以来, 伴随着我国经济的高速发展, 生态环境日趋恶化.中国并不是第一个陷入工业文明导致环境困境的国家, 20世纪30—60年代, 因区域工业化快速发展而导致的八大环境公害事件中(世界八大环境公害事件包含1930年12月的比利时马斯河谷烟雾事件、1931年的日本富山"痛痛病"事件、1943年开始的美国洛杉矶光化学烟雾事件、1948年10月的美国多诺拉烟雾事件、1952年12月的英国伦敦烟雾事件、1950年日本熊本县水俣病事件、1959年日本四日市哮喘病事件及1968年3月日本爱知县的米糠油事件), 受灾国家包括比利时、美国、英国及日本.经济增长与环境退化之间的潜在冲突是可持续发展的辩论核心, 为了有效治理污染问题, 国务院在1983年将环境保护确立为基本国策, 更于2013年9月制定了《大气污染防治行动计划》(即《大气十条》), 提出包含减少污染物排放、优化产业结构与能源结构、提高科技创新能力、建立区域协作机制等治理计划.建设生态文明是实现可持续发展的内在要求, 如何在环境维护与经济建设之间取得平衡更是目前中国所面临的重要课题.因此, 考察环境库兹涅茨曲线(environmental Kuznets curve)将是中国实现可持续发展的重要途径之一.
在环境库兹涅茨曲线的实证研究方面, 研究人员大多选取人均地区生产总值作为经济发展指标, 随着环境恶化指标、研究所关心的地域层级及使用的模型方法不同, 所呈现的环境库兹涅茨曲线形状也因此不同.运用中国数据的相关研究约始于1999年, 张晓(1999)利用非线性回归模型分析了中国大气污染物与人均地区生产总值之间的环境库兹涅茨曲线.近年来, 李健等(2019)以空气质量未达二级的天数为空气污染指标, 研究了京津冀的区域环境库兹涅茨曲线, 发现在此指标下环境库兹涅茨曲线为倒N形; 张昭利等(2012)使用30个省、直辖市、自治区的二氧化硫浓度数据研究发现, 二氧化硫浓度与经济增长的关系为倒N形.同样是使用省直辖市、自治区的数据, 范丹(2014)、Hao等(2016)及Kang等(2016)基于空间动态面板数据分析了人均二氧化碳排放与经济增长的关联, 考虑了不同的模型及空间权重, 结果都发现基于人均二氧化碳排放的环境库兹涅茨曲线基本满足倒U形关系, 空间效应明显, 并且考虑了空间效应后拐点会更高.
近年来, 在众多空气污染物中, 又以可入肺颗粒物(PM2.5)引起社会大众与政府部门的高度重视.因为具有粒径小的特性, PM2.5能够通过气管, 进入细支气管与肺泡, 甚至可以通过肺泡毛细血管进入血管, 进而损害人体的呼吸系统及心血管系统(Pope et al., 2002;Peters, 2005).PM2.5是空气动力学直径小于或等于2.5 μm的颗粒物的统称, 其构成和来源较二氧化碳、氮氧化物等单一污染物更为复杂, 其成分来源有两种, 分别是自然源与人为源, 且以人为源为主, 包括道路扬尘、工业粉尘、化石燃料的燃烧等.另外, PM2.5也可因生成过程的不同分为两种类型:1由自然界、人类活动或污染源直接产生的, 称为一次排放; 2由大气中的气态物质, 如二氧化硫、氮氧化物、有机挥发物(VOC)等经过物理化学反应生成的, 称为二次生成.由于二次生成反应的缘故, PM2.5的污染水平很难直接从污染源的排放量推算出来, 必须通过源解析才能得到污染的来源及贡献量.2018年, 北京市环境保护局针对PM2.5来源解析的研究表明, 北京市该年PM2.5的主要来源中, 本地排放占2/3, 其中, 移动源(机动车)、扬尘源(如建筑施工及道路扬尘)及工业排放分别占本地排放的45%、16%及12%(北京市环境保护局于2018年5月14日发布的新闻稿请见http://sthjj.beijing.gov.cn/bjhrb/xxgk/jgzn/jgsz/jjgjgszjzz/xcjyc/xwfb/832588/index.html).上述特征表明, PM2.5不是单一的污染物, 而是一种综合性的环境污染指标.目前, 中国经济发展所依赖的高能耗生产方式及其所依赖的能源结构, 在污染排放的约束下将面临巨大挑战.
关于PM2.5的研究, 早期着重于污染浓度与气象条件的关系, 然后才开始研究污染的成分及来源.Lyu等(2016)对1997—2012年中国污染的成因进行了分析, 结果表明, 总颗粒物排放的变化归因于初级颗粒物、二氧化硫及氮氧化物排放的变化, 而经济增长效应和能源强度效应则是影响这一时期大气污染物排放变化的两个关键驱动因素.在PM2.5与经济发展的研究中, 多以线性模型分析空气污染与工业活动、能源效率、产业结构、交通运输等经济变量的相关性(孙建如等, 2015; 王珍等, 2018).在非线性模型的研究中, 马丽梅等(2014)利用2001—2010年的省级数据分析雾霾的溢出效应, 得到中国当时尚未存在倒U形的环境库兹涅茨曲线的结论, 并且说明了区域间联防联控的重要性; Hao等(2016)运用空间模型研究了2013年73城市PM2.5污染水平的影响因素, 发现存在倒U形环境库兹涅茨曲线; 同时, 邵帅等(2016)利用空间动态面板数据研究省级反演的PM2.5水平, 分别考虑地理矩阵和经济矩阵, 把污染回归到空间项及经济变量上, 发现在1998—2012年, PM2.5的库兹涅茨曲线为U形, 即倒N形的左半边; 王立平等(2010)基于省级环境库兹涅茨曲线的研究发现, 地理空间权重矩阵的系数比经济空间权重矩阵的系数更为显著, 即中国环境污染主要原因在地理上有溢出效应.
基于此, 本文以PM2.5浓度作为环境恶化的指标, 以人均生产总值作为地区经济发展指标, 使用各产业生产值度量各产业的经济规模, 探讨环境质量与地区经济发展程度的关联.在目前运用实际PM2.5污染数据的研究中, 尚未有学者使用同时控制空气污染时滞性与空间溢出效应的模型设定, 因此, 本文基于大气污染物的物理特性, 使用动态空间滞后模型, 对经济增长和大气污染的关系进行估计.另外, 基于中国战略发展与政策所需, 并考虑西部地区的特殊性, 本文将中国分成两大区块, 进行分地区的环境库兹涅茨曲线分析.最后本文对二氧化硫排放量和氮氧化物排放量的环境库兹涅茨曲线进行探讨.
2 数据与方法(Data and method)本文采用中国气象局网站实时发布的PM2.5数据(2013—2017年)、中国统计局公布的二氧化硫排放数据(2004—2017年)和氮氧化物排放数据(2011—2017年)及中国统计年鉴中的经济数据进行分析.
在方法上, 本文采用空间计量模型中的动态空间面板模型对污染数据进行研究.空间计量模型使用空间权重矩阵描述地区之间或个体之间的互动关系, 在面板数据的空间计量模型中, 研究人员可以借由考虑个体效应及时间效应来控制不随个体变化的因素及不随时间变化的因素.由于加入了因变量的空间滞后项, 导致模型产生内生解释变量问题, 使得最小二乘法的系数估计值是有偏的, 因此, 需要使用其他的估计方法以完善估计量的统计性质.其中, 动态空间面板数据模型的估计方法中, Yu等(2008)提供了偏误校正的极大似然估计量, 但需满足条件"当样本中的个体维度(N)和时间维度(T)都趋向于无穷大", 换言之, "当T趋向于无穷大时, 相对N来说T不能太小"; 广义矩估计方法主要是在Arellano等(1991)及Blundell等(1998)的基础上进行扩展, 主要有Elhorst(2010b)提出的最优广义矩估计及Lee等(2014)的有效广义矩估计, Parent等(2010)则给出了马尔科夫链蒙特卡罗的系数估计方法.由于本文所使用的数据的时间维度小于个体维度, 不适合使用极大似然估计, 因此, 本研究的分析采用广义矩估计方法.
在不同变量的空间效应上, 被解释变量的空间效应和解释变量的空间效应通常比误差项之间的空间效应更为重要:当忽略前者时, 剩余参数估计量的估计会失去一致性, 而当忽略后者时, 剩余参数估计量的估计只会失去有效性.因此, 本文使用动态空间滞后模型刻画空气污染物的空间传播特性与时间滞后性质.给定区域i, 包含固定效应的一阶动态空间滞后模型可以写为:
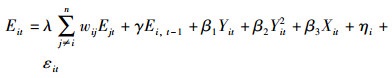
|
(1) |
式中, E为度量污染水平的指标, 本文中一共考虑了PM2.5浓度水平(μg·m-3)、二氧化硫排放量(103t)及氮氧化物(NOx)排放量(103t), Y为人均地区生产总值(GDPPC, 万元), X为各产业地区生产总值(亿元), 下标i与j表示地区, t表示时刻, t-1表示t时刻的前一时刻, 就是时间上的滞后项.在参数部分, λ用来度量空气污染的地理溢出效应, γ用来度量空气污染的时间滞后效应, β用来度量解释变量对空气污染水平的影响, ηi与εit分别为个体效应与扰动项.
本文考虑了3种空间权重矩阵.首先, 空间权重矩阵Wg采用相邻空间矩阵, 该矩阵主对角线上的元素为0, 当区域i与区域j相邻时, 元素wij为1, 不相邻时为0.在实证分析时, 可以通过行标准化的处理使区域i的空间滞后项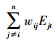
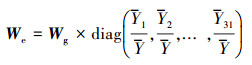
|
(2) |
式中, 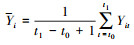
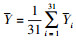
使用动态空间滞后面板模型分析中国省级库兹涅茨曲线得到表 1, 全国水平的模型表示见下:
| 表 1 PM2.5空气质量与人均地区生产总值的拟合结果 Table 1 Estimation results between PM2.5 and GDP per capita |
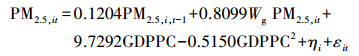
|
(3) |
此结果与本文预期相符:PM2.5的时间滞后项在5%水平下显著为正, 说明PM2.5水平与上期水平正相关, 在其他因素不变的情况下, 过去污染越高的地区现在污染水平也会较高, 平均而言, 某一年PM2.5的污染水平提高1 μg·m-3会致使该地区下一年的污染水平上升0.1204 μg·m-3; PM2.5空间滞后项在0.1%水平下显著为正, 说明空气污染在地理空间上有溢出效应, 临近地区的空气质量较差者, 本地的空气质量也较差, 一般来说, 一地的邻近地区平均PM2.5污染水平提高1 μg·m-3会导致该地污染浓度升高0.8099 μg·m-3.此结果进一步表示在空气质量的治理上应采取区块治理, 如果只有本地的污染排放下降, 也可能受临近地区的影响而导致其努力成果在空气质量的提升上表现有限; 人均地区生产总值的一次和二次回归系数在5%水平下均显著, 并且一次系数为正, 二次系数为负, 判断环境库兹涅茨曲线的形状为倒U形, 并利用一阶导数为零的特性求得拐点处的人均地区生产总值为94458.25元, 如图 1所示.由于人均地区生产总值的系数在3次方模型中不显著, 因此, 判断在不含其他控制变量的情况下, 空气污染与人均地区生产总值的环境库兹涅茨曲线为二次形式.
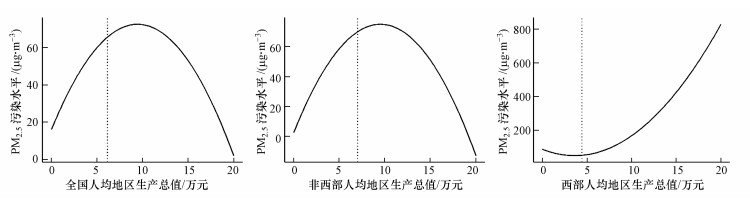 |
| 图 1 PM2.5空气质量与人均地区生产总值的拟合曲线(图中虚线为数据最后一年的各省人均地区生产总值均值, 下同) Fig. 1 Estimation curves between PM2.5 and GDP per capita |
接着, 本文将"西部大开发"所涵盖的区域, 共计10个省级行政区划分为西部地区, 其余省级行政区为非西部地区(将我国划分为东部、中部、西部3个地区的时间始于1986年, 由全国人大六届四次会议通过的"七五"计划正式公布.目前, 西部地区包括的省级行政区共12个, 分别是四川、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆、广西、内蒙古.国务院于2000年正式成立西部地区开发领导小组, 确定西部大开发的目的是"把东部沿海地区的剩余经济发展能力, 用以提高西部地区的经济和社会发展水平、巩固国防".因本文数据范围不包含西藏自治区, 且考虑到直辖市的特殊性, 此处将重庆市列入非西部地区, 故西部地区共有10个省级行政单位, 非西部地区有20个).本文针对两种分区皆拟合了二次模型与三次模型, 结果人均地区生产总值的3次方系数均不显著, 因此, 确定空气污染与人均地区生产总值的关系为二次形式.
表 1第3列为非西部地区的回归拟合结果, 模型表示见式(4).从回归结果可以看出, 空气污染的空间滞后项系数为正, 并且在0.1%水平下显著, 说明空气质量确实会受临近地区的空气污染程度影响; 另外, 在5%水平下, 人均地区生产总值的一次系数为正、二次系数为负, 呈现倒U形的环境库兹涅茨曲线.利用一阶导数为零的特性求得拐点处的人均地区生产总值为95186.96元, 此数值相较全国整体的拐点要低, 说明非西部地区对于到达污染峰值所需的经济要求相对较低.
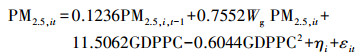
|
(4) |
西部地区的拟合结果则见表 1第4列, 模型表示见式(5).可以发现其结果与第3列非西部地区的结果大相径庭:尽管空气污染的空间溢出性依然存在, 并且在0.1%水平下为正, 但人均地区生产总值的系数都不显著, 退化回一个不含控制变量的纯空间自回归过程.在只考虑人均地区生产总值的情况下, 西部地区的空气污染主要受临近区域的扩散影响, 而与本地的人均地区生产总值相对无关.
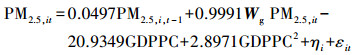
|
(5) |
由于工业产业生产与空气污染相关, 产出越高, 所需投入的要素越多, 对资源的需求因而提高, 并且在技术提升有限、产业尚未转型的时期, 作为副产品所排放的污染也会随之增加.本文将各产业产量纳入回归模型作为控制变量, 所得到的全国估计结果如表 2所示.表 2的回归模型拟合结果说明, 在加入各产业产量后, 污染的时间滞后项、空间滞后项及人均地区生产总值系数显著结果均与表 1一致, 拐点位于99097.15元.而在各产业产量方面, 则有第一产业产量与空气污染水平在0.5%水平下负相关的结果.与前述的分析过程相同, 本文亦进行基于人均地区生产总值三次方的模型分析, 以得到更为严谨的模型拟合结果, 发现人均地区生产总值三次方系数并不显著, 由此确认PM2.5的环境库兹涅茨曲线在加入各产业产量后仍为二次形式.
| 表 2 加入各产业产量的拟合结果 Table 2 Estimation results with production output |
表 2第3列显示了非西部地区加入各产业产量的模型拟合结果, 其中, 空气污染的时间滞后项系数在5%水平下为正, 空间溢出效应在0.1%水平下为正, 表示空气质量会受上期空气质量及邻近区域空气质量的影响.人均地区生产总值的一次项系数在5%水平下显著为正, 二次项系数在5%水平下显著为负, 由图 2可知, 该结果表现出倒U形的库兹涅茨曲线, 拐点位于人均地区生产总值为98043.85元的位置, 略低于全国水平拐点位置, 而各产业产量对于PM2.5浓度均没有显著影响.
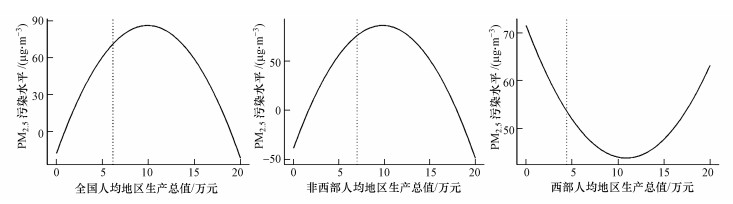 |
| 图 2 加入各产业产量的拟合曲线 Fig. 2 Estimation curves with production output |
西部地区加入各产业产量的模型拟合结果见表 2第4列, 空气污染的空间滞后项系数在0.1%水平下为正, 一次产业产量在5%水平下显著为负, 说明西部地区的空气质量水平主要受临近地区的污染扩散及当地第一产业生产活动影响, 当地农业生产活动越发达, 空气污染浓度越低.原因可能在于空气质量过差会致使第一产业产量减少(杨泳冰等, 2016; 丁振峰, 2018), 西部地区的第一产业占比又比较高(西部地区第一产业占比为12.47%, 非西部地区为7.32%), 因此, 第一产业经济规模较高的西部省份, 空气质量一般也较好.
综上所述, 由于中国西部地区经济产业发展结构的特殊性, 使其环境库兹涅茨曲线的特征与其他省级行政区不同.在非西部地区, 空气污染存在时间滞后性、空间溢出效应, 环境库兹涅茨曲线是倒U形的, 并且各产业产量对空气污染没有显著的影响.而在西部地区, 空气污染依然存在空间溢出效应, 并且第一产业的产量对空气质量有显著影响, 然而人均地区生产总值与空气质量之间并不存在显著的趋势.
3.3 加入经济权重的库兹涅茨曲线分析为了考虑地区之间可能有不对称的影响, 本文又在相邻矩阵基础上增加了各省的地区生产总值权重, 认为经济发展较高的邻省对本省污染的影响可能比较剧烈, 因此, 给予经济发展相对好的邻省比较高的权重.使用空间权重矩阵We进行分析的模型拟合结果见表 3, 由拟合结果刻画的环境库兹涅茨曲线见图 3.
| 表 3 加入经济权重的拟合结果 Table 3 Estimation results with economic weights |
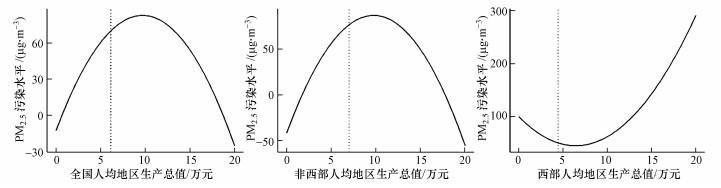 |
| 图 3 加入经济权重的拟合曲线 Fig. 3 Estimation curves with economic weights |
表 3第1列为中国整体在原空间矩阵上经过经济加权后的拟合结果, 可以发现与表 2结论一致:估计结果依然具有显著的时间滞后项及空间滞后项, 在5%显著水平下, 人均地区生产总值的系数呈现一次为正、二次为负, 表现为拐点位于96901.16元处的倒U形环境库兹涅茨曲线.
类似的, 依照西部大开发政策涵盖的范围将中国分为西部10省与非西部20省, 其中, 非西部地区使用经济加权空间矩阵的拟合结果如表 3第3列所示, 其结论亦没有因空间权重矩阵的调整而有所变化:时间滞后项与空间滞后项均显著地影响空气污染水平; 在5%显著水平下, 环境库兹涅茨曲线呈现倒U形, 拐点位于97423.71元, 并且各产业产量对于PM2.5浓度都没有显著影响, 与表 2结论一致.非西部地区的模型拟合结果见表 3第4列, 与表 2结论类似, 只有空间滞后项于0.1%水平下显著, 说明西部地区的空气质量水平主要受临近地区的污染扩散影响, 而尚未出现显著的环境库兹涅茨曲线.
综上所述, 本文使用地区生产总值调整后的空间权重矩阵进行模型拟合, 所得到的分析结论与原结论一致, 说明本文结论对于空间权重矩阵并不敏感, 不会因为空间权重矩阵的调整导致结果迥异, 因而具有稳健性.
3.4 使用污染传输矩阵权重的库兹涅茨曲线分析为了更细致地刻画各省之间PM2.5的空间传播机制, 本文进而使用薛文博等(2014;2018)的污染传输矩阵作为空间权重矩阵.由于该传输矩阵是基于CAMx空气质量模型的颗粒物来源追踪技术对PM2.5的跨区域输送进行模拟, 因此比简单的相邻矩阵更加精确.利用此污染传输矩阵作为空间权重矩阵, 得到表 4的模型拟合结果与图 4的环境库兹涅茨拟合曲线.
| 表 4 使用污染传输矩阵的拟合结果 Table 4 Estimation results using pollution transport matrix |
 |
| 图 4 使用污染传输矩阵的拟合曲线 Fig. 4 Estimation curves using pollution transport matrix |
表 4展示了污染传输矩阵权重Wt的拟合结果, 其中, 第2列与第3列是全国水平与非西部地区的回归拟合结果.在全国水平与非西部地区的结果中, PM2.5污染的时间滞后项与空间滞后项都显著为正, 人均地区生产总值的一次项系数显著为正、平方项系数显著为负, 拐点分别位于103635.84元及99562.64元, 呈现倒U型的环境库兹涅茨曲线, 非西部地区的拐点位置略低于全国平均水平的拐点位置, 并且各产业产量对于污染水平都没有显著影西部地区的拐点位置略低于全国平均水平的拐点位置, 并且各产业产量对于污染水平都没有显著影响.由表 4第4列发现, 西部地区的PM2.5污染水平主要受到临近地区的污染扩散及第一产业产量影响, 与全国水平及非西部地区的机制有所不同.
综上所述, 本文为了更细致地刻画各省之间PM2.5污染相互影响的机理, 使用污染传输矩阵作为空间权重矩阵进行模型拟合, 所得到的分析结论与原结论一致, 再次表明本文结论具有稳健性.
4 其他大气污染物的环境库兹涅茨曲线估计结果(Estimation results of environmental Kuznets curve for other air pollutants)由于PM2.5数据的时间跨度较短, 本文一并考虑了其他大气污染指标进行研究, 包括二氧化硫排放量和氮氧化物排放量.其中, 二氧化硫排放量的数据跨度是2004—2017年, 氮氧化物排放量的数据跨度是2011—2017年, 排放数据皆源于中国统计局.
4.1 二氧化硫排放量的环境库兹涅茨曲线分析表 5与图 5显示了二氧化硫排放量的环境库兹涅茨曲线估计结果, 在全国水平及非西部地区的结果都是时间与空间滞后系数显著, 第三产业产量系数显著为负, 并且人均地区生产总值的一次项系数显著为正、二次项系数不显著, 环境库兹涅茨曲线处于上升阶段.西部地区的估计结果也呈现时间与空间滞后系数显著, 并且人均地区生产总值的一次项系数显著为正、二次项系数显著为负, 出现倒U形的结构.
| 表 5 二氧化硫加入经济权重的拟合结果 Table 5 Estimation results with economic weights for SO2 |
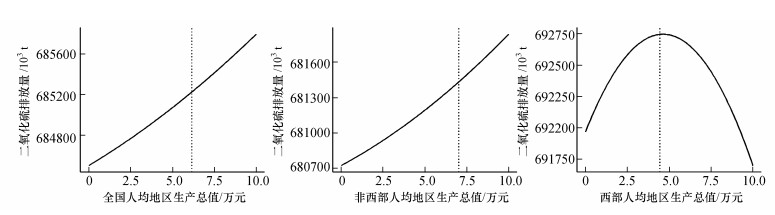 |
| 图 5 二氧化硫加入经济权重的拟合曲线 Fig. 5 Estimation curves with economic weights for SO2 |
表 6为氮氧化物排放量的环境库兹涅茨曲线估计结果, 在全国水平及非西部地区的结果都是时间与空间滞后系数显著, 第一产业产量系数显著为负, 并且人均地区生产总值的一次项系数显著为正、二次项系数不显著, 由图 6发现环境库兹涅茨曲线还在上升阶段.西部地区的氮氧化物排放量估计结果只有时间滞后项与空间滞后项的系数显著为正.
| 表 6 氮氧化物加入经济权重的拟合结果 Table 6 Estimation results with economic weights for NOx |
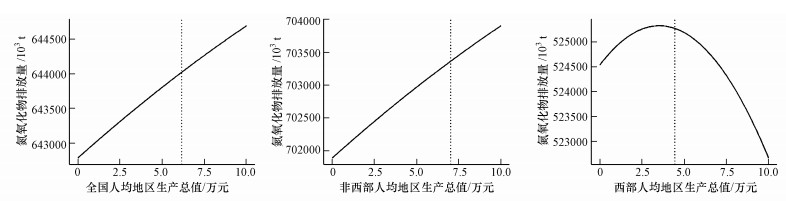 |
| 图 6 氮氧化物加入经济权重的拟合曲线 Fig. 6 Estimation curves with economic weights for NOx |
综上所述, 尽管不同大气污染物排放量的环境库兹涅茨曲线在同时控制时间滞后及空间滞后的模型下呈现不同的形状, 但它们的时空滞后项系数都是显著的, 说明在研究空气污染时, 使用同时控制时间滞后项及空间溢出效应的模型设定能够更精确地刻画污染物的特性.
5 结论(Conclusions)本文基于中国30个省份2013—2017年的面板数据, 实证分析了PM2.5的环境库兹涅茨曲线的存在性及空间溢出性, 结果发现, 总体上中国的PM2.5污染水平依照经济发展程度呈现先恶化后改善的模式, 同时中国整体的PM2.5污染具有显著的空间溢出性.
6 建议(Suggestions)根据研究结论, 本文提出以下政策建议:首先, 由于PM2.5污染存在极为显著的空间溢出性, 说明当一个区域以环境超载的方式来发展经济时, 除造成本地的污染问题外, 还会影响到邻近地区的环境质量, 所以在治理环境时, 必须注重区域之间的合作, 否则将拉低治理成效.因此, 亟需地方政府间充分沟通协调, 以制定区域联合环境管理的规范和违约的应对机制, 如污染补偿机制、利益协调机制等, 并且通过共享环境信息以加强联合执法与监督的力度; 再者, 促进跨区域的环境合作, 以形成空气污染控制的有效治理模式.
其次, 由于区域间的经济发展与污染结构不同, 在区域协同治理的同时也需要考虑地区的独特性, 针对不同区域制定不同的排放目标及治理措施, 贯彻因地制宜的治理策略, 例如:加强西部地区与非西部地区的节能减排技术交流, 调整区域发展目标以避免西部各省因过度追求生产而成为高污染、高能耗产业转移的阵地等, 这样才能从根本上取得经济发展与环境保护的平衡, 实现可持续发展, 建设生态文明美好家园.
Aderson H R, Ponce de Leon A, Bland J M, et al. 1996. Air pollution and daily mortality in London:1987-1992[J]. British Medical Journal, 312(7032): 665-669. DOI:10.1136/bmj.312.7032.665 |
Andreoni J, Levinson A. 2001. The simple analytics of the environmental Kuznets curve[J]. Journal of Public Economics, 80(2): 269-286. DOI:10.1016/S0047-2727(00)00110-9 |
Anselin L. 1988. Spatial Econometrics:Methods and Models[M]. Netherlands: Springer.
|
Arellano M, Bond S. 1991. Some tests of specification for panel data:Monte Carlo evidence and an application to employment equations[J]. Review of Economic Studies, 58: 277-297. DOI:10.2307/2297968 |
Baltagi B H. 2005. Econometric Analysis of Panel Data(3rd Edition)[M]. Chichester, West Sussex: John Wiley.
|
Bayer P, Keohane N, Timmins C. 2009. Migration and hedonic valuation:The case of air quality[J]. Journal of Environmental Economics and Management, 58(1): 1-14. |
Blundell R, Bond S. 1998. Initial conditions and moment restrictions in dynamic panel data model[J]. Journal of Econometrics, 87(1): 115-143. |
Bond A S. 1991. Some tests of specification for panel data:Monte Carlo evidence and an application to employment equations[J]. The Review of Economic Studies, 58(2): 277-297. |
Byrne M M. 1997. Is growth a dirty word? Pollution, abatement and endogenous growth[J]. Journal of Development Economics, 54(2): 261-284. DOI:10.1016/S0304-3878(97)00043-6 |
丁振峰, 张良, 徐翔. 2018. 空气污染对我国粮食安全的冲击-以冬小麦为例[J]. 生态经济, 34(5): 183-188. |
Elhorst J P. 2010. Dynamic panels with endogenous interaction effects when t is small[J]. Regional Science and Urban Economics, 40(5): 272-282. DOI:10.1016/j.regsciurbeco.2010.03.003 |
范丹. 2014. 中国二氧化碳EKC曲线扩展模型的空间计量分析[J]. 宏观经济研究, (5): 83-91. |
Fang C, Liu H, Li G, et al. 2015. Estimating the impact of urbanization on air quality in China using spatial regression models[J]. Sustainability(Switzerland), 7(11): 15570-15592. |
Farzin Y H, Bond C A. 2006. Democracy and environmental quality[J]. Journal of Development Economics, 81(1): 213-235. DOI:10.1016/j.jdeveco.2005.04.003 |
Georgiev E, Mihaylov E. 2015. Economic growth and the environment:reassessing the environmental Kuznets Curve for air pollution emissions in OECD countries[J]. Letters in Spatial and Resource Sciences, 8(1): 29-47. DOI:10.1007/s12076-014-0114-2 |
Grossman G M, Krueger A B. 1991. Environmental impacts of a North American Free Trade Agreement[J]. Social Science Electronic Publishing, 8(2): 223-250. |
Hao Y, Liu Y. 2016. The influential factors of urban PM2.5 concentrations in China:A spatial econometric analysis[J]. Journal of Cleaner Production, 112: 1443-1453. DOI:10.1016/j.jclepro.2015.05.005 |
Hao Y, Liu Y, Weng J, et al. 2016. Does the environmental Kuznets curve for coal consumption in China exist? New evidence from spatial econometric analysis[J]. Energy, 114: 1214-1223. DOI:10.1016/j.energy.2016.08.075 |
Kang Y Q, Zhao T, Yang Y Y. 2016. Environmental Kuznets curve for CO2 emissions in China:a spatial panel data approach[J]. Ecological Indicators, 63: 231-239. DOI:10.1016/j.ecolind.2015.12.011 |
Kelejian H H, Prucha I R. 1998. A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances[J]. The Journal of Real Estate Finance and Economics, 17(1): 99-121. DOI:10.1023/A:1007707430416 |
Lee L F. 2004. Asymptotic distributions of quasi-maximum likelihood estimators for spatial econometric models[J]. Econometrica, 72(6): 1899-1925. DOI:10.1111/j.1468-0262.2004.00558.x |
Lee L F. 2007. GMM and 2SLS estimation of mixed regressive, spatial autoregressive models[J]. Journal of Econometrics, 137(2): 489-514. |
Lee L F, Yu J. 2010. Estimation of spatial autoregressive panel data models with fixed effects[J]. Journal of Econometrics, 154(2): 165-185. |
Lee L F, Yu J. 2014. Efficient GMM estimation of spatial dynamic panel data models with fixed effects[J]. Journal of Econometrics, 180(2): 174-197. |
Lesage J P. 1997. Bayesian estimation of spatial autoregressive models[J]. International Regional Science Review, 20(1/2): 113-129. |
李鹏. 2014. 环境库茨涅茨倒U形曲线在西部地区的现实考证-基于空间面板数据的研究[J]. 经济研究参考, (57): 39-44. DOI:10.3969/j.issn.2095-3151.2014.57.004 |
李龚. 2016. 基于PM2.5指标的中国环境库兹涅茨曲线估计[J]. 统计与决策, (23): 21-25. |
李健, 靳泽凡, 苑清敏. 2019. 京津冀空气质量环境库兹涅茨曲线及影响因素-基于2006-2017年面板数据的分析[J]. 生态经济, 35(2): 197-201+218. |
刘伯龙, 袁晓玲, 张占军. 2015. 城镇化推进对雾霾污染的影响-基于中国省级动态面板数据的经验分析[J]. 城市发展研究, 22(9): 23-27+80. DOI:10.3969/j.issn.1006-3862.2015.09.004 |
卢晓彤, 卢忠宝, 宋德勇. 2012. 基于阈值面板模型的我国环境库兹涅茨曲线假说再检验[J]. 管理学报, 9(11): 1689-1696. DOI:10.3969/j.issn.1672-884X.2012.11.017 |
Lyu W, Li Y, Guan D, et al. 2016. Driving forces of Chinese primary air pollution emissions:an index decomposition analysis[J]. Journal of Cleaner Production, 133(Complete): 136-144. |
马丽梅, 张晓. 2014. A spatial econometric approach to studying regional air pollution in China[J]. China Economist, 9(4): 42-56. |
Ord K. 1975. Estimation methods for models of spatial interaction[J]. Journal of the American Statistical Association, 70(349): 120-126. DOI:10.1080/01621459.1975.10480272 |
Ordás Criado C, Valente S, Stengos T. 2011. Growth and pollution convergence:Theory and evidence[J]. Journal of Environmental Economics and Management, 62(2): 199-214. |
Parent O, Lesage J P. 2010. A spatial dynamic panel model with random effects applied to commuting times[J]. Transportation Research Part B:Methodological, 44(5): 633-645. DOI:10.1016/j.trb.2010.01.004 |
Peters A. 2005. Particulate matter and heart disease:Evidence from epidemiological studies[J]. Toxicology and Applied Pharmacology, 207(2 Suppl.): 477-482. |
Pope C, Burnett R, Thun M, et al. 2002. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution[J]. Journal of the American Medical Association, 287: 1132-1141. DOI:10.1001/jama.287.9.1132 |
邵帅, 李欣, 曹建华, 等. 2016. 中国雾霾污染治理的经济政策选择-基于空间溢出效应的视角[J]. 经济研究, 51(9): 73-88. |
孙建如, 钟韵. 2015. 我国大城市PM2.5影响因素的经济分析-基于市级面板数据的实证研究[J]. 生态经济, 31(3): 62-65+77. DOI:10.3969/j.issn.1671-4407.2015.03.013 |
王立平, 管杰, 张纪东. 2010. 中国环境污染与经济增长:基于空间动态面板数据模型的实证分析[J]. 地理科学, 30(6): 818-825. |
Wang S, Wang Z, Zhou C, et al. 2017. The characteristics and drivers of fine particulate matter(PM2.5) distribution in China[J]. Journal of Cleaner Production, 142: 1800-1809. DOI:10.1016/j.jclepro.2016.11.104 |
王珍, 宋晓霞. 2018. PM2.5影响因素实证分析-基于省级面板数据[J]. 价值工程, 37(24): 273-276. |
薛文博, 付飞, 王金南, 等. 2014. 中国PM2.5跨区域传输特征数值模拟研究[J]. 中国环境科学, 34(6): 1361-1368. |
薛文博, 雷宇, 许艳玲. 2018. 2000-2016年气象条件变化对全国PM2.5污染影响数据集[M]. 北京: 中国环境出版社.
|
杨泳冰, 易福金, 胡浩. 2016. 农业环境对粮食生产收益的新挑战-以近地面臭氧污染下的冬小麦种植为例[J]. 中国农村经济, (9): 72-82. |
Yu J, de Jong R, Lee L. 2008. Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large[J]. Journal of Econometrics, 146(1): 118-134. |
张晓. 1999. 中国环境政策的总体评价[J]. 中国社会科学, (3): 88-99. |
张昭利, 任荣明, 朱晓明. 2012. 我国环境库兹涅兹曲线的再检验[J]. 当代经济科学, 34(5): 23-30+124. |
朱冉, 赵梦真, 薛俊波. 2018. 产业转移、经济增长和环境污染-来自环境库兹涅茨曲线的启示[J]. 生态经济, 34(7): 68-73. |
 2020, Vol. 40
2020, Vol. 40


