2. 东北农业大学 水利与土木工程学院, 哈尔滨 150030;
3. 哈尔滨学院 信息工程学院, 哈尔滨 150086;
4. 黑龙江省农业科学院 农村能源与环保研究所, 哈尔滨 150086
2. School of Conservancy&Civil Engineering, Northeast Agricultural University, Harbin 150030;
3. School of Information Engineering, Harbin University, Harbin 150086;
4. Rural Energy&Environmental Protection Institute, Heilongjiang Academy of Agricultural Sciences, Harbin 150086
近年来, 伴随着河流水污染事件的相继发生, 国内外学者逐渐重视对河流水污染预警溯源方面的研究(史斌等, 2017;姜继平等, 2017b).从水环境污染的监管治理角度出发, 河流水污染溯源分析是河流水环境监管和保护工作的重要任务之一.一方面, 如果采用人工走访, 环保监管工作效率低下, 加上监管人员水平不齐, 对污染偷排、暗管排放难以确认, 对环境监察监管形成巨大挑战.另一方面, 污染企业众多, 污染特征识别不清, 导致不能及时获取有效的河流水污染源头信息(李彩鹦, 2013).因此, 在水污染发生后, 研究如何快速、准确重构河流水污染排放历史, 找出污染源的位置、掌握其污染强度、获知污染事件发生的初始条件及边界条件等问题, 对于保证河流水污染快速准确的应急响应、提高水环境风险防范能力及水污染应急管理水平具有非常重大的现实意义.
水污染溯源通常包括定性的源解析(Source apportionment)和定量的源反演(Source inversion)两类.其中, 污染源反演主要是利用定量的溯源手段获取河流污染物的来源, 同时复原、重构河流污染物与潜在风险源之间联系的过程(周慧平等, 2014).水污染溯源方法起源于大气污染的溯源研究, 由于地下水环境更加稳定, 污染源反演方法已经广泛应用于地下水中并且取得了良好的效果(杨一帆和张凯山, 2013;白玉堃等, 2019;张双圣等, 2019).随着经济的发展, 河流水污染事件频发, 河流水污染源反演技术也逐渐受到了广泛的关注, 常见方法包括输出系数法(陈源华等, 2011;Chen等, 2011)、多元统计方法(Shrestha和Kazama, 2007;Varol和Sen, 2009)、概率模拟方法(Neupauer和Wilson, 2001)以及优化求解方法(Mahar和Datta, 2001)等.Chen等(2011)开发了基于一维污染物迁移模型和相关系数优化法的污染反演方法, 并基于示踪剂实验进行了不确定性分析研究, 在实际工程中有一定的应用价值;谢婷婷等(2019)采用多元回归方法构建了叶绿素a浓度反演模型以评价水体的富营养化程度.基于输出系数法、多元统计的水污染源反演方法简单易行, 但是对污染物排放历史的重构精度还难以保证.程伟平和廖锡健(2011)提出了一种反向概率密度方法识别地表水污染源;Zhang和Huang(2017)利用反向概率方法识别地表水污染源的排放时间和排放地点, 并通过假想案例验证方法的可行性;姜继平等(2017a)采用贝叶斯方法实现了对河流水污染的定量溯源研究.基于概率模拟的水污染源反演方法需要依靠大量的先验信息对模型参数进行概率估计, 然而对于河流水污染事件的先验信息往往很难及时获取.Datta等(2008)结合非线性优化方法和污染物迁移模型, 提出了一种基于污染源反演的动态监测网络设计方法, 结果表明通过监测网络数据的动态反馈功能, 能够有效地提高污染源反演的效率;辛小康等(2014)结合遗传算法和数学分析方法, 利用控制方程的适应度值, 实现河流污染源项参数的反演和识别;王军强(2018)以一维水质扩散模型为基础, 构建了以人工智能算法为核心的河流突发污染源项识别框架, 实现对突发水污染的定量溯源反演分析.基于优化求解的水污染源反演方法, 根据河流水质模型和监测数据, 反向拟合受纳水体的污染负荷或浓度, 从而识别污染源位置、排放时间和排放量等排放历史信息, 该类方法计算效率高且运行相对稳定(Jha和Datta, 2013;刘洁等, 2020).由于环境系统固有的复杂性与不确定性, 大多数优化求解算法对于单参数的污染源反演问题求解效果较好, 多参数的联合求解精度还有待提高.与大多数优化求解方法相比, 遗传算法, 作为启发式优化算法, 通过模仿自然环境中的生物遗传和进化现象优化求解河流水污染排放历史, 对于解决非线性复杂问题具有很好的适用性(Liu et al., 2017).
因此, 本研究利用美国特拉基河示踪剂实验获得的河流水污染应急监测数据, 结合多种群遗传算法和自适应遗传算法, 提出改进遗传算法(Improved Genetic Algorithm, IGA), 对河流水污染排放历史(排放地点、排放时间、排放量)进行重构, 实现河流水污染定量源反演分析, 旨在为河流水污染精准溯源与治理提供科学的技术支撑.
2 研究区域与数据(Study area and data) 2.1 研究区概况特拉基河起源于美国加利福尼亚州的太浩湖, 流经特拉基镇、里诺市和斯帕克斯市, 最终注入内华达州的金字塔湖, 河流全长约为195 km, 流域面积约为7925 km2(Condon et al., 2015).特拉基河作为内陆河, 为流域城镇居民提供必要的生活饮用水.因此, 特拉基河的水污染问题将直接影响着流域居民的生产生活和用水安全.
2.2 示踪剂实验与应急监测数据美国地质勘探局分别在2006年和2007年对特拉基河进行了3次示踪剂实验, 将罗丹明染料注入到河流3个不同流量(4.05至75.32 m3·s-1)的地点.其中, 2007年5月22日22:30将0.82 kg罗丹明染料注入到特拉基河上游1号监测断面, 下游的2~6号监测断面分别对河流中罗丹明染料浓度进行监测, 流量变化范围为4.05~18.04 m3·s-1, 为低流量情景1.2006年6月29日06:05将1.30 kg罗丹明染料注入到特拉基河中游5号监测断面, 下游的6~8号监测断面分别对河流中罗丹明染料浓度进行监测, 流量变化范围为64.00~58.90 m3·s-1, 为高流量情景2.2006年6月27日07:01将0.46 kg罗丹明染料注入到特拉基河下游9号监测断面, 下游的10~12号监测断面分别对河流中罗丹明染料浓度进行监测, 流量变化范围为36.16~43.61 m3·s-1, 为中流量情景3.美国地质勘探局通过对特拉基河高、中、低不同流量的3个河段进行示踪剂实验, 研究特拉基河不同河段的污染物迁移转化的特性.本研究根据示踪剂实验所收集的罗丹明染料浓度的监测数据(Crompton, 2008), 以特拉基河为研究对象, 开展河流瞬时点源污染的定量源反演研究, 识别罗丹明染料的投放地点、投放时间以及投加量, 进而重构特拉基河3次不同流量情景下的示踪剂排放历史, 验证基于改进遗传算法IGA的河流水污染源反演方法的可靠性与稳定性.具体示踪剂实验监测断面布设情况, 如表 1所示.
| 表 1 特拉基河示踪剂实验监测断面布设情况 Table 1 The layout of monitoring site in Truckee River for river tracer experiments |
根据特拉基河的特征, 本研究将针对一维河流瞬时点源污染, 采用一维对流弥散方程模拟地表河流中污染物的运输和迁移过程, 公式如下(Ding et al., 2017):
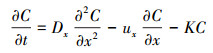
|
(1) |
式中, C代表t时刻地表河流x处污染物浓度(mg·L-1);t代表时间(min);ux代表污染物在河水流动方向x上的输移速度(m·min-1);Dx代表污染物在河水流动方向x上的弥散系数(m2·min-1);K代表污染物降解系数(min-1);ux·∂C/∂x代表Δt时间段内污染物在河水流动方向x上的浓度变化;Dx·∂2C/∂x2代表湍流扩散所引起的污染物在河水流动方向x上的浓度变化.初始条件和边界条件如下(Gao et al., 2016):
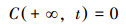
|
(2) |
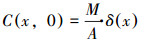
|
(3) |
式中, M代表污染物在时间t0=0时刻进入河流的总质量(kg), A代表河流的断面面积(m2), 其中, A=Q/u.δ(x)为狄拉克函数, 当x=0时, δ(x)=1;当x≠0时, δ(x)=0.因此, 一维地表水瞬时点源排放模型的解析解如下(Zeng et al., 2018):

|
(4) |
结合公式(4), 污染物源反演方法利用已知的河道水力特征(河流断面流量Q、河流断面平均速度u、河流离散系数D和污染物降解系数K)(姜继平等, 2017b)和下游监测断面的污染物浓度监测数据, 反向拟合受纳水体的污染负荷或浓度, 重构并识别污染源历史排放相关参数, 包括污染物排放位置x0, 污染物排放时间t0以及污染物排放总量M.通过最小化污染物浓度监测值与水质模型模拟值的差的平方和来构建优化模型.优化模型如下:
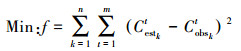
|
(5) |
式中, n代表监测断面的数量;m代表监测时刻的数量;Ctestk代表第k个监测断面在第t个监测时刻的污染物模拟值;Ctobsk代表第k个监测断面在第t个监测时刻的污染物监测值.通过最小化河水中污染物浓度的模拟值与监测值之间的误差, 重构并识别污染源历史排放相关参数.
3.2 改进遗传算法IGA传统遗传算法通过随机生成单个种群进行搜索求解, 具有收敛速度快、鲁棒性高等特点.但是存在局部搜索效率较低, 容易出现早熟收敛的问题.多种群遗传算法可以同时随机生成多个子种群, 分别按照不同的进化策略和遗传算子在相同的搜索空间中并行进行搜索求解.通过将总体中的最优个体传播到其他子种群中实现不同子种群个体之间的相互交流和协同进化(杨斌等, 2019).自适应遗传算法则可以动态调整交叉和变异概率, 使得个体能够自适应搜索空间的特点(Srinivas et al., 1994).因此, 本研究将多种群遗传算法和自适应遗传算法相结合, 提出改进遗传算法IGA, 在保证最优个体稳定进化的同时, 增加各个子种群的多样性, 提高算法的局部搜索能力, 进而有效避免单个种群在进化过程中出现的早熟收敛现象.具体遗传操作如下:
3.2.1 适应度函数本研究污染物浓度的模拟值Cest可由一维河流水质模型计算得到.污染物浓度的观测值Cobs可由下游的各个监测断面测量得到.通过最小化污染物浓度监测值与水质模型模拟值的差的平方和来构建优化模型.因此, 多种群遗传算法的适应度函数见公式(5).
3.2.2 选择操作本研究采用轮盘法, 根据适应度函数值从每一代种群中选择优势个体.同时, 为了避免适应度高的个体在轮盘法选择过程中被淘汰, 采用最优个体保存策略, 将一定比例(精英率Best)的最优个体直接复制到下一代中, 本研究精英率Best设为0.1.
3.2.3 交叉和变异操作为了提高遗传算法性能, 减少种群进化过程中陷入局部收敛的可能性, 本研究采用自适应交叉概率Pcro和变异概率Pmut, 以提高改进遗传算法的局部搜索能力, 具体计算公式参考陈闯等(2019).根据经验, 本研究将交叉概率取值设定在0.7和0.9之间, 变异概率取值设定在0.001和0.01之间(陈闯等, 2019).
3.2.4 移民操作在种群进化过程中, 移民操作通过选择子种群中适应度最高的个体, 并将其传播到其他子种群中来实现各个子种群之间信息的交换.通过移民操作可以加快优良个体在总体中的传播速度, 优化改进遗传算法的收敛速度, 进而提高最优解的计算精度.通过多次试算, 本研究执行移民操作的判断准则为当3个子种群中的最优个体的适应度值连续10代保持不变时, 执行移民操作.本研究迭代计算的终止的收敛准则为当种群进化到第200代的时候, 算法即可终止.
3.3 计算流程改进遗传算法IGA的算法流程, 如图 1所示.基本计算步骤如下:
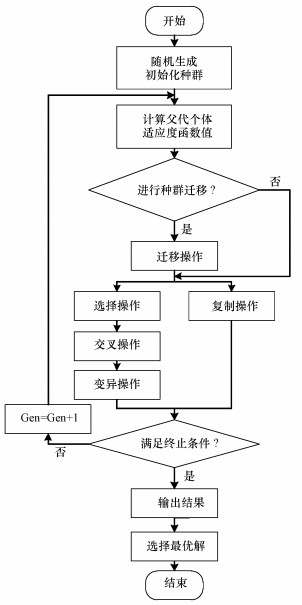 |
| 图 1 改进遗传算法流程示意图 Fig. 1 Flow chart of the IGA |
(1) 随机初始化种群, 确定子种群的数量P和子种群的规模N;
(2) 进入迭代进化过程:
a) 根据适应度函数计算当前环境下各个子种群中父代个体的适应度函数值;
b) 比较各个种群内所有个体的适应度值, 取前10%的个体作为精英个体, 直接复制为下一子代个体;
c) 对每个子种群剩余个体分别执行选择、交叉和变异操作, 得到各个子种群的子代个体.将产生相同数目的精英个体和进化个体共同组合为新一代子种群;
d) 计算各个新一代子种群中个体的适应度函数值, 若其中3个子种群中的最优个体适应度函数值没有发生变化的进化代数达到10代, 则将当前的最优个体传播到其他的子种群中;
e) 重复步骤(a)~(d), 直到算法达到收敛准则;
(3) 当满足终止条件时, 记录各个子种群的输出结果, 并在各个子种群的输出结果中选择最优解.
不同的种群个体规模、交叉率、变异率、复制率和种群进化代数等对目标函数、计算时间、算法收敛性有较大的影响.本研究通过多次试算, 优化筛选改进遗传算法的初始化参数, 以提高算法的收敛性和准确性.选取最优算法相关参数设置如下:初始化子种群数量P=10, 子种群个体规模N=100, 最大迭代次数T=200, 精英率Best=0.1.
4 结果与讨论(Results and discussion)本研究将改进遗传算法IGA应用于美国特拉基河的示踪剂实验中, 结合一维对流扩散方程模拟污染物运输迁移特征, 对高、中、低流量3个不同情景下的示踪剂排放历史, 包括初始污染物排放位置x0、污染物排放时间t0、污染物排放总量M进行定量源反演分析, 验证IGA算法在实际河流水污染源反演分析中的可靠性和稳定性, 为实现河流水污染精准溯源与治理提供可靠保障.
4.1 改进遗传算法进化结果分析本研究根据美国特拉基河的高、中、低流量3次示踪剂实验监测结果, 采用IGA算法对初始污染物排放位置x0、污染物排放时间t0、污染物排放总量M进行优化求解.根据美国特拉基河的高、中、低流量3次示踪剂实验监测结果, 得到IGA算法的种群进化过程如图 2所示.由图 2可知, 高、中、低流量3种情景下, IGA算法均在种群进化至155~160代时, 目标函数值达到最优值, 且整体保持一定的稳定性.由于IGA算法中子种群之间的移民操作, 整体进化曲线呈阶梯式下降的特点逐渐收敛, 且无震荡的趋势.在低流量条件下的示踪剂实验(情景1)中, 适应度函数值比较大, 这是由于低流量示踪剂实验监测站点较多, 监测数据充足, 适应度函数为整个系统观测值与预测值的离差平方和, 是系统总的误差的积累.而情景2和情景3的监测站点较少, 对应的监测数据较少, 因此, 系统总的误差积累相对较小, 适应度函数值比较小.综上所述, IGA收敛速度相对较快, 针对不同情境下的示踪剂实验反演分析, 算法运行相对稳定, 可以保证初始污染物排放位置x0、污染物排放时间t0和污染物排放总量M, 3个参数优化计算的稳定性.
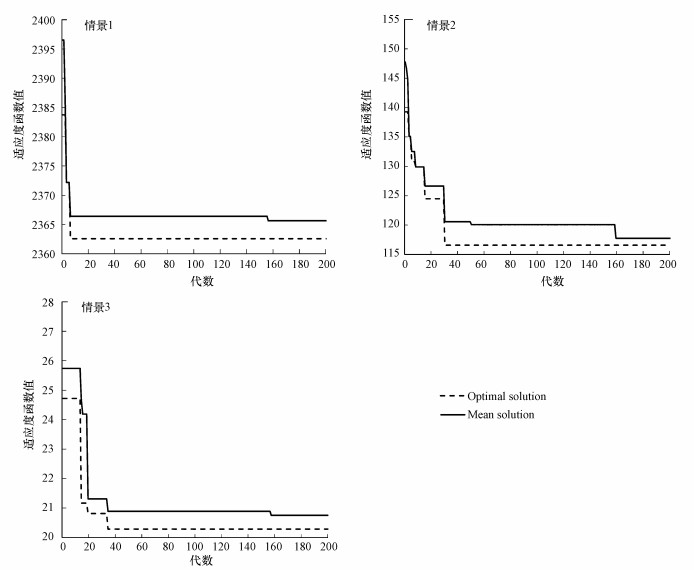 |
| 图 2 IGA算法进化曲线 Fig. 2 Evolution curve by IGA algorithm |
根据美国特拉基河的高、中、低流量3次示踪剂实验监测结果, 针对3次示踪剂实验分别运行IGA算法50次, 选择5组较优结果, 以减少计算误差.高、中、低流量示踪剂实验下, 示踪剂的定量反演分析结果, 如表 2所示.结果表明, 情景1低流量下的示踪剂排放地点距监测站点2上游约为[9704.36, 10064.64] m, 排放时间约为2007年5月23日12:00之前的[89.29, 91.47] min, 排放量约为[0.79, 0.84] kg.示踪剂排放历史(排放地点、排放时间、排放量)的反演分析结果的相对误差分别为1.24%、0.85%、2.30%.情景2高流量下的示踪剂排放地点距监测站点6上游约为[7503.62, 8046.36] m, 排放时间约为2006年6月29日12:00之后的[363.40, 368.83] min, 排放量约为[1.24, 1.29] kg.示踪剂排放历史(排放地点、排放时间、排放量)的反演分析结果的相对误差分别为2.42%、0.66%、2.14%.情景3中流量下的示踪剂排放地点距监测站点10上游约为[7400.76, 7774.07] m, 排放时间约为2006年6月27日12:00之后的[413.68, 422.34] min, 排放量约为[0.45, 0.47] kg.示踪剂排放历史(排放地点、排放时间、排放量)的反演分析结果的相对误差分别为2.13%、0.48%、2.02%.其中, 排放时间t0的反演分析结果好于排放地点x0和排放量M.情景3的示踪剂排放历史的重构和识别要好于情景1和情景2, 这是由于情景1和情景2中的监测数据较多, 算法很难寻找到一个最优解可以同时保证每个模拟值和监测值的差最小.因此, 在河流水污染定量源反演的过程中, 应急监测网络的优化布设, 包括应急监测断面和污染物监测频率的设定, 均影响着水污染排放历史重构的准确性.综上所示, IGA算法在实际河流水污染源反演分析中具有一定的准确性和可靠性.对高、中、低不同流量下的3次示踪剂实验均可以较好地识别、重构示踪剂排放历史.对于实际河流水污染源反演误差均在可接受范围内.
| 表 2 示踪剂实验污染源定量反演分析结果 Table 2 Pollution source inversion results for the trace experiments |
本研究采用改进遗传算法IGA对河流水污染排放历史进行定量反演分析, 并将该方法应用于美国特拉基河的示踪剂实验中, 以验证IGA算法的可靠性与稳定性, 从而实现河流水污染定量源反演分析, 为河流水污染精准溯源与治理提供科学的技术支撑.
1) 结合多种群遗传算法和自适应遗传算法, 构建了基于IGA算法的河流水污染定量反演方法, 对河流水污染排放历史(排放量、排放时间、排放地点)进行重构, 实现河流水污染的定量源反演分析.
2) 以美国特拉基河示踪剂实验为基础, 验证了基于IGA算法的河流水污染源反演方法的可靠性和稳定性.结果表明:IGA算法在实际河流水污染源反演分析中具有一定的可靠性和稳定性.低流量下的示踪剂排放历史(排放地点、排放时间、排放量)反演分析结果的相对误差分别为1.24%、0.85%、2.30%.高流量下的反演分析结果的相对误差分别为2.42%、0.66%、2.14%.中流量下的反演分析结果的相对误差分别为2.13%、0.48%、2.02%.对高、中、低不同流量下的3次示踪剂实验均可以较好地重构和识别示踪剂排放历史.对于实际河流水污染源反演分析的误差均在可接受范围内.
3) 在河流水污染定量源反演的过程中, 应急监测断面布置和污染物监测频率的设定, 均会影响水污染排放历史重构的准确性.因此, 为了提高河流水污染定量源反演分析的准确性, 未来将重点围绕应急监测网络的优化布设方法进行研究.
白玉堃, 卢文喜, 李久辉. 2019. 卡尔曼滤波方法在地下水污染源反演中的应用[J]. 中国环境科学, 39(8): 3450-3456. |
Chen Y H, Peng W, Jiang J P, et al. 2011. Contaminant point source identification of rivers chemical spills based on correlation coefficients optimization method[J]. China Environmental Science, 31(11): 1802-1807. |
Condon L E, Gangopadhyay S, Pruitt T. 2015. Climate change and non-stationary flood risk for the upper Truckee River basin[J]. Hydrology and Earth System Sciences, 19(1): 159-175. DOI:10.5194/hess-19-159-2015 |
Crompton E J. 2008. Traveltime Data for the Truckee River between Tahoe City, California, and Vista, Nevada, 2006 and 2007[R]. U.S. Geological Survey
|
陈闯, Chellali R, 邢尹. 2019. 改进遗传算法优化BP神经网络的语音情感识别[J]. 计算机应用研究, 36(02): 344-346. |
陈媛华, 王鹏, 姜继平, 等. 2011. 基于相关系数优化法的河流突发污染源项识别[J]. 中国环境科学, 31(11): 1802-1807. |
程伟平, 廖锡健. 2011. 基于逆向概率密度函数的一维污染源排放重构[J]. 水动力学研究与进展, 26(4): 460-469. |
Datta B, Chakrabarty D, Dhar A. 2008. Optimal Dynamic Monitoring Network Designand Identification of Unknown Groundwater Pollution Sources[J]. Water Resources Management, 23(10): 2031-2049. |
Ding X W, Wang S Y, Jiang G H, et al. 2017. A simulation program on change trend of pollutant concentration under water pollution accidents and its application in Heshangshan drinking water source area[J]. Journal of Cleaner Production, 167: 326-336. DOI:10.1016/j.jclepro.2017.08.094 |
Gao J, Zeng L J, Wu L, et al. 2016. Solution for sudden contamination transport through air duct system:Under a puff release[J]. Building and Environment, 100: 19-27. DOI:10.1016/j.buildenv.2016.01.024 |
Jha M, Datta B. 2013. Three-dimensional groundwater contamination source identification using adaptive simulated annealing[J]. Journal of Hydrologic Engineering, 18(3): 307-317. DOI:10.1061/(ASCE)HE.1943-5584.0000624 |
姜继平, 董芙嘉, 刘仁涛, 等. 2017a. 基于河流示踪实验的Bayes污染溯源:算法参数、影响因素及频率法对比[J]. 中国环境科学, 37(10): 3813-3825. DOI:10.3969/j.issn.1000-6923.2017.10.025 |
姜继平, 王鹏, 刘洁, 等. 2017b. 突发水污染预警应急响应研究与实践的方法学辨析[J]. 环境科学学报, 37(9): 3621-3628. |
Liu J, Guo L, Jiang J P, et al. 2017. Emergency material allocation and scheduling for the application to chemical contingency spills under multiple scenarios[J]. Environmental Science and Pollution Research, 24(1): 956-968. DOI:10.1007/s11356-016-7811-x |
刘洁, 陈昊辉, 张丰帆, 等. 2020. 基于改进遗传算法的河流水质模型多参数识别[J]. 东北农业大学学报, 51(1): 73-82. |
李彩鹦. 2013.污水化学指纹数据库的构建及其在水污染溯源中的应用[D].北京: 北京化工大学. 1-2 10.7666/d.Y2392966
|
Mahar P S, Datta B. 2001. Optimal identification of ground-water pollution sources and parameter identification[J]. Journal of Water Resources Planning Management, 127: 20-29. DOI:10.1061/(ASCE)0733-9496(2001)127:1(20) |
Neupauer R M, Wilson J L. 2001. Adjoint-derived location and travel time probabilities for a multi-dimensional groundwater system[J]. Water Resources Research, 37: 1657-1668. DOI:10.1029/2000WR900388 |
Shrestha S, Kazama F. 2007. Assessment of surface water quality using multivariate statistical techniques:a case study of the Fuji river basin, Japan[J]. Environmental Modelling & Software, 22(4): 464-475. |
Srinivas M, Patnaik L M. 1994. Adaptive probabilities of crossover and mutation in Genetic Algorithms[J]. IEEE transactions on systems, man and cybernetics, 24(4): 656-667. DOI:10.1109/21.286385 |
史斌, 姜继平, 王鹏. 2017. 基于高频在线水质监测数据异常预警的突发污染预警[J]. 中国环境科学, 37(11): 4394-4400. |
Varol M, Sen B. 2009. Assessment of surface water quality using multivariate statistical techniques:a case study of Behrimaz Stream, Turkey[J]. Environmental Monitoring and Assessment, 159(1/4): 543-553. |
王军强. 2018.阿什河流域突发环境事件应急决策支持系统研究[D].哈尔滨: 哈尔滨工业大学. 33-39 http://cdmd.cnki.com.cn/Article/CDMD-10213-1018894508.htm
|
谢婷婷, 陈芸芝, 卢文芳, 等. 2019. 面向GF-1 WFV数据的闽江下游叶绿素a反演模型研究[J]. 环境科学学报, 39(12): 4276-4283. |
辛小康, 韩小波, 李建, 等. 2014. 基于遗传算法的水污染事故污染源识别模型[J]. 水电能源科学, 7: 52-55. |
杨斌, 陈振宇, 阮文骏, 等. 2019. 基于多种群协同进化遗传算法的智能小区需求响应调度策略[J]. 电力需求侧管理, 21(02): 16-20. |
杨一帆, 张凯山. 2013. 突发型大气污染源位置识别反演问题的数值模拟[J]. 环境科学学报, 33(9): 2388-2394. |
Zeng L J, Du B W, Zhang R Y, et al. 2018. Probability-based inverse characterization of the instantaneous pollutant source within a ventilation system[J]. Building and Environment, 143: 378-389. DOI:10.1016/j.buildenv.2018.07.036 |
Zhang X, Huang M. 2017. Ensemble-based release estimation for accidental river pollution with known source position[J]. Journal of Hazardous Materials, 333: 99-108. DOI:10.1016/j.jhazmat.2017.03.028 |
张双圣, 强静, 刘汉湖, 等. 2019. 基于贝叶斯公式的地下水污染源识别[J]. 中国环境科学, 39(4): 1568-1578. |
周慧平, 高燕, 尹爱经. 2014. 水污染源解析技术与应用研究进展[J]. 环境保护科学, (6): 19-24. |
 2020, Vol. 40
2020, Vol. 40


