2. 哈尔滨工业大学城市水资源与水环境国家重点实验室, 哈尔滨 150090;
3. 中国建筑第二工程局有限公司, 北京 100000
2. State Key Laboratory of Urban Water Resource and Environment, Harbin Institute of Technology, Harbin 150090;
3. China Construction Second Engineering Bureau Ltd., Beijing 100000
伴随着城市化发展进程的日益加快, 城市不透水地面比率增加, 下垫面渗透能力降低, 自然系统调蓄能力减弱(Nguyen et al., 2019; Jiang et al., 2018).自然排水系统的改变导致暴雨径流量、峰值流量、污染物排放量的大幅增加, 进而导致受纳水体水质严重恶化(Eckart et al., 2017;贺文彦等, 2018).海绵城市作为新一代城市雨洪管理技术, 能够统筹发挥人工干预和自然系统的功能, 通过“渗、滞、蓄、净、用、排”功能, 从源头上实现径流削减与污染物控制, 保障城市的水安全与水环境(俞孔坚等, 2015;车伍等, 2015).
为精准有效地实现城市雨水的管理管控, 国内外学者采用SWMM、MIKE URBAN和InfoWorks CS等水文模型对各类海绵城市源头减排措施进行模拟评价(Garrido-Baserba et al., 2020;马冰然等, 2019; Askarizadeh et al., 2015).目前针对源头减排设施组合方案的模拟评价已开展了大量研究, 主要集中在组合设施与单一设施的雨水控制效果对比(王运涛等, 2020)、既有设计方案中组合设施的水文水质效益评价(朱寒松等, 2019)及组合设施的成本效益分析(高曼等, 2019)等方面, 而对源头减排设施组合方案定量化设计研究少有报道(Baek et al., 2015; Men et al., 2020).同时, 海绵城市建设作为一项综合性生态工程, 应从成本、水文、水质等多方面进行综合决策与效果评价(Saadatpour et al., 2020; Raei et al., 2019;陶涛等, 2019), 目前鲜见结合优化算法的海绵城市规划与评价研究.随着海绵城市技术体系与评价标准日趋完善(杨正等, 2020), 开展如何选择源头减排设施的类型与面积、如何判定研究区海绵城市规划效果的综合性研究尤为迫切.
本研究综合海绵城市建设成本、雨水径流控制率和污染物削减率, 构建NSGA-II多目标优化算法, 结合层次分析法实现海绵城市优化方案的综合评价, 同时基于全年降雨和多种暴雨场景, 利用SWMM模型对海绵城市规划效果进行全面评估, 为海绵城市的优化设计与合理布局提供参考.
2 材料与方法(Materials and methods) 2.1 研究区概况A中心城区(研究区)位于江西省中东部, 规划用地面积2655.0 km2, 地处长江三角洲、珠江三角洲, 位于抚河中游, 属亚热带湿润气候区, 年平均降水量1856 mm, 最大降雨量年2308.8 mm, 最少年降雨量1133.6 mm.雨量分布不均匀, 其中4—6月占全年降水量的48%, 1—3月占22%, 7—9月占19%, 10—12月占11%.年平均无霜期258 d, 年平均日照时数为1725.6 h, 年平均风速1.4 m·s-1, 多年平均蒸发量为1443.2 mm.土壤主要类型以红壤为主, 土壤的渗透性较好, 滞水现象不严重.
根据研究区地势与用地布局规划, 研究区规划共划分6个雨水排水分区:城北一区排水分区、城北二区排水分区、城中一区排水分区、城中二区排水分区、城西排水分区和城东排水分区, 以下简称为城北一区、城北二区、城中一区、城中二区、城西区和城东区.研究区雨水排水分区如图 1所示.
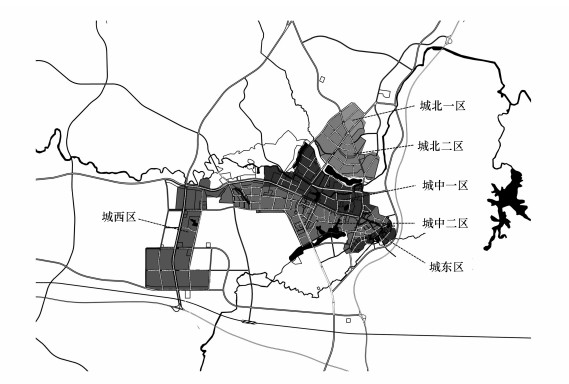 |
| 图 1 研究区雨水排水分区 Fig. 1 Stormwater drainage zoning plan |
基于快速分类的非支配遗传算法(NSGA-Ⅱ算法)是Deb等在NSGA的基础上提出的一种多目标优化算法(Deb et al., 2002).近年来, NSGA-II作为目前最流行的主流多目标遗传算法之一, 已被成功地应用到许多工程领域(刘冬梅等, 2016).
基于NSGA-II多目标遗传算法, 以源头减排设施建设费用、研究区雨水综合径流系数和源头减排设施污染物综合去除率为目标函数, 以年径流总量控制率最低目标和源头减排设施建设最大面积作为边界条件, 通过模型迭代进化得到最优化帕累托解集, 实现海绵城市源头减排设施的规划设计.
2.2.2 目标函数海绵城市源头减排设施系统布局的目标函数综合考虑了建设费用、雨水径流控制效果和径流污染物控制效果, 计算如公式(1)~(4)所示:
(1) 源头减排设施建设费用
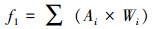
|
(1) |
式中:i为第i种源头减排设施;Ai为第i种源头减排设施建设面积(m2);Wi为第i种源头减排设施建设单价(元· m2).
(2) 研究区雨水综合径流系数

|
(2) |
式中:Ci为第i种源头减排设施捕获比;ψi为第i种源头减排设施径流系数;ψ′为研究区建成区综合径流系数;S0为研究区新建/改造区面积(m2);S1为研究区建成区面积(m2);S为研究区总面积(m2).
(3) 源头减排设施污染物综合去除率
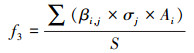
|
(3) |
式中:βi, j为第i种源头减排设施对第j种污染物的去除率;
σj为第j中污染物的污染物综合权重.
(4) 多目标优化总目标函数
以源头减排设施建设费用最小化、研究区雨水综合径流系数最小化、源头减排设施污染物综合去除率最大化为优化目标, 联合公式(1)、(2)、(3), 得到总目标函数:
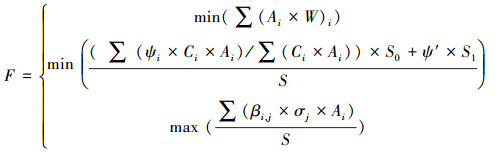
|
(4) |
结合研究区实际现状与水质需求, 选择绿色屋顶、透水铺装、下凹绿地、生物滞留池、植草沟和雨水花园6种源头减排设施(许萍等, 2016;符锐等, 2014), 选择COD、氨氮、总磷和悬浮物四种主要污染物作为评价对象, 本研究各类设施的基础参数见表 1.
| 表 1 源头减排设施基础参数 Table 1 Basic parameters of source emission reduction facilities |
为更加准确地获得海绵城市源头减排设施的面积分布, 结合研究区土地利用规划与海绵城市建设需求, 在多目标优化模型以源头减排设施建设面积和雨水年综合径流系数为约束条件:
(1) 源头减排设施建设面积
各类源头减排设施面积Ai应小于其建设上限, 并且源头减排设施径流控制面积之和应不低于新建/改建区总面积的80%, 即
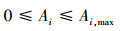
|
(5) |
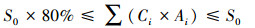
|
(6) |
式中:Ai, max为第i种源头减排设施设面积上限.
根据研究区的土地利用规划与城市建设现状, 对应的源头减排设施建设面积范围见表 2.
| 表 2 各类源头减排设施可设置的面积范围 Table 2 The area range of source emission reduction facilities |
(2) 雨水年综合径流系数
研究区地处《海绵城市建设技术指南——低影响开发雨水系统构建》划分的Ⅳ类区域, 其年径流总量控制率应处于70%~85%之间, 为保证源头减排设施的雨水径流控制效果达到年径流总量控制率的控制要求, 雨水年综合径流系数应低于0.3, 即
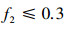
|
(7) |
多目标优化模型计算得到的帕累托最优解集往往含有若干最优解(Liu et al., 2014), 因此, 需要结合研究区实际条件与需求迫切程度进行多指标综合评价.层次分析法能够根据总评价目标进行连续型分解, 得出各层评级目标, 依据最下层指标计算综合评分指数, 确定最优化方案(郭金玉等, 2008).本文以源头减排设施建设费用、研究区雨水综合径流系数和源头减排设施污染物综合去除率为最低因素层, 通过专家问卷调查汇总结果进行各因素的重要性排序, 构建判断矩阵得出各因素权重系数, 根据权重系数及归一化处理结果, 计算帕累托最优解集中各方案的综合评分指数, 确定最优化海绵城市建设方案.
2.3 SWMM模型构建 2.3.1 排水系统概化结合研究区的地形地势、土地利用规划、建筑分布、管网走向、行政边界以及雨水排水管网的排水分区现状, 共计划分236个子汇水区域.根据研究区管网规划完成模型雨水排水管网网络概化, 研究区共计划分1734个管段、1763个检查井、31个排放口和5个泵站, 研究区SWMM模型概化结果见图 2.
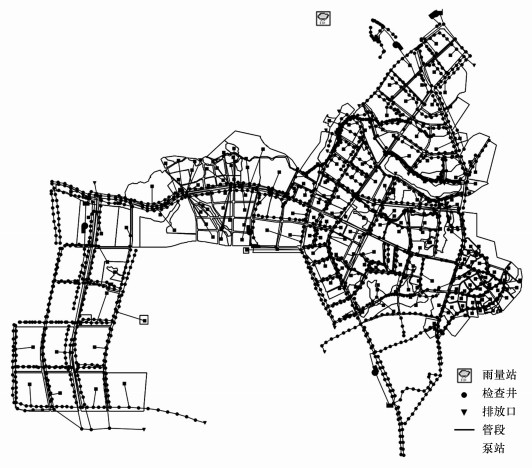 |
| 图 2 研究区SWMM模型概化图 Fig. 2 Generalization diagram of SWMM model in study area |
为对研究区海绵城市源头减排设施的雨水径流量、污染物量控制效果进行准确全面的分析, 采用不同重现期降雨和2019年实际年降雨两种降雨的边界条件进行模拟计算.其中2019年研究区全年共产生降雨79场, 累计降雨天数148 d, 累计降雨量1816 mm, 降雨时间序列如图 3a所示.
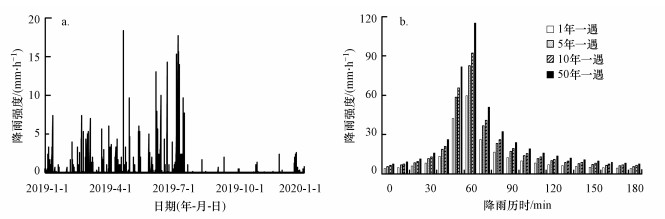 |
| 图 3 降雨强度图(a) 2019年实际降雨强度, (b)各重现期降雨强度 Fig. 3 Rainfall time series graph (a) Actual rainfall in 2019, (b)Rainfall in different return recurrence periods |
重现期降雨数据参考按照研究区最新的暴雨强度公式进行重现期雨量计算.暴雨强度公式:
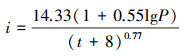
|
(8) |
式中:i 为设计暴雨强度(mm·min-1);t为降雨历时(min);P为暴雨重现期(年).
本文参考研究区暴雨强度公式, 采用芝加哥雨型, 设置雨峰系数为0.3分别代入P = 1、5、10和50(年), t = 180 min, 计算统计得到各重现期条件下暴雨强度-时间序列曲线, 如图 3b所示.其中P =1、5、10和50(年)时, 降雨总量分别为45.96、63.63、71.23和88.90 mm.
2.3.3 模型基础参数设置研究区SWMM模型采用Horton下渗模型、动力波方程管网汇流模型、指数函数污染物累积模型和指数污染物冲刷模型4种水文、水力和水质模型.通过SWMM用户手册查阅和文献调研, 确定模型主要参数设置(赵冬泉等, 2011), 具体参数设置见表 3.
| 表 3 SWMM模型主要参数设置 Table 3 SWMM model main parameter settings |
SWMM模型中源头减排设施的参数包括表层和内层结构参数, 其中表层参数包括蓄水深度、植物体积覆盖率、表面粗糙系数、表面坡度等, 内层参数包括土壤层厚度、蓄水层厚度、导水率、孔隙比、堵塞因子等(侯精明等, 2019).源头减排设施主要模型参数见表 4, 其余模型设置参数由文献调研和SWMM用户手册获得(何爽等, 2013;胡爱兵等, 2015).
| 表 4 源头减排设施主要模型参数设置 Table 4 Main parameter settings of source emission reduction facilities |
通过NSGA-II算法进行多目标优化求解, 得到包含200组源头减排设施建设方案的帕累托最优解集, 模型计算结果见图 4, 其中每个最优解都包含大量信息, 包括6种源头减排设施的建设面积、总建设成本、年综合径流系数及综合污染物控制率.分析多目标优化结果可知, 方案中雨水径流系数的减小与污染物综合去除率的提高伴随着源头减排建设成本的显著增加.根据研究区实际现状与需求, 建设成本控制优先级最高, 雨水径流控制次之, 径流污染物控制最低.
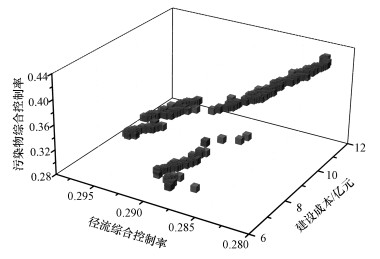 |
| 图 4 多目标优化帕累托解集 Fig. 4 Multi-objective optimization Pareto solution set |
采用层次分析法对200组源头减排设施建方案进行综合评价, 根据判断矩阵计算得, 源头减排总建设成本、年综合径流系数及综合污染物控制率指标的权重系数分别为0.637、0.258和0.105.根据指标权重系数及方案归一化处理结果, 对总评价目标进行综合评价, 计算综合评分指数, 得到综合建设成本、雨水径流控制能力及污染物控制率三项指标的最优方案.根据研究区土地利用规划, 综合海绵城市规划目标与指标, 对于规划新建区与改造区进行海绵城市设计, 将源头减排设施最优方案分配到各排水分区及各子汇水区, 得出最终的建设方案.各源头减排设施布置情况的模型示意见图 5.
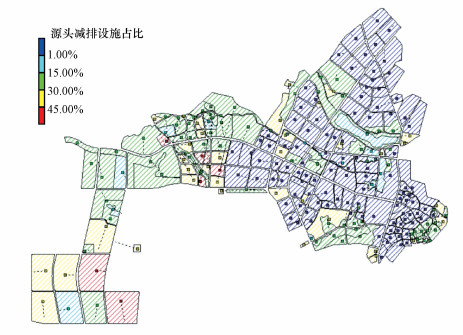 |
| 图 5 最优方案模型示意图 Fig. 5 The schematic diagram of the optimal solution model |
根据2019年实际降雨情况, 模拟分析得到海绵建设和非海绵建设的两种情景下降雨径流的变化, 分析海绵城市源头减排建设前后全年降雨分配情况(图 6), 相较于非海绵建设, 海绵城市建设后雨水蒸发量、下渗量分别由8.5%和46.9%提高至11.6%和58.4%, 总径流量由44.6%降低到29.9%, 相应的年径流总量控制率由55.4%提高至70.1%, 满足海绵城市建设标准.从长历时降雨的角度分析, 海绵设施在每场降雨中都相应地起到了控制径流的作用, 实现全年总径流的削减.
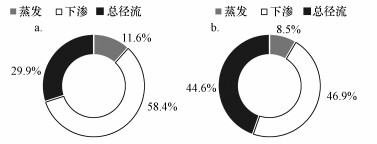 |
| 图 6 2019年全年降雨分配情况(a)海绵建设, (b)非海绵建设 Fig. 6 Annual rainfall distribution of 2019 (a) Sponge City Construction, (b) Non-sponge city construction |
根据暴雨强度公式, 设计重现期分别为1年、5年、10年和50年四场短历时暴雨事件, 统计分析模型模拟结果, 得到四种重现期短历时暴雨事件下研究区的降雨-总径流过程曲线(图 7).模拟结果显示, 随着暴雨强度的增大, 研究区峰值流量大幅增加.相对于非海绵建设, 海绵建设能有效削减汇水区径流峰值流量, 且峰值流量的削减效果随降雨强度增加而减小, 在1年一遇、5年一遇、10年一遇和50年一遇的降雨条件下, 研究区径流峰值削减率分别达到了46.6%、44.9%、44.1%和41.2%.
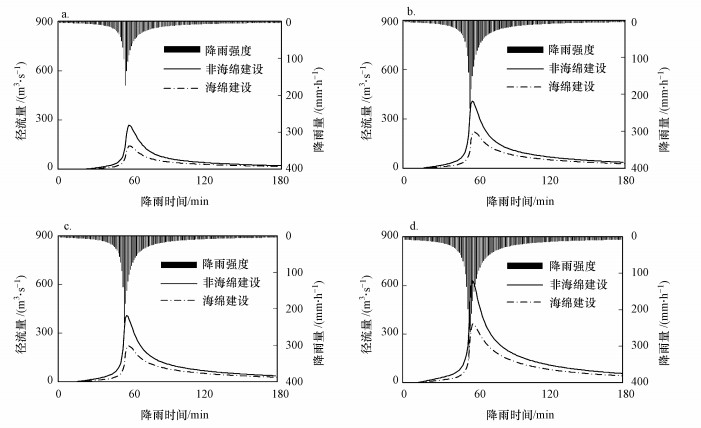 |
| 图 7 不同重现期降雨强度下总径流变化曲线(a) 1年一遇, (b) 5年一遇, (c) 10年一遇, (d) 50年一遇 Fig. 7 Curve of total runoff under different rainfall intensity in different recurrence period (a) R1, (b) R5, (c) R10, and (d) R50 |
在四场短历时暴雨条件下, 分析统计海绵城市建设前后雨水排放口雨水径流量变化.以源头减排设施建设区的排放口为例进行雨水溢流量统计分析(图 8), 在暴雨强度较小时, 源头减排设施能够充分发挥其“渗”、“滞”、“蓄”功能, 对暴雨径流有效削减, 大幅延后峰值出现时间;随着暴雨强度逐渐加大, 源头减排设施对于短历时暴雨径流峰值的削减能力逐渐减弱, 径流峰值延后时间逐渐缩短.在1年一遇、5年一遇、10年一遇和50年一遇的降雨条件下, 排放口径流峰值流量分别降低71.6%、43.1%、35.1%和28.5%, 径流峰值出现时间延后42、29、24和15 min.
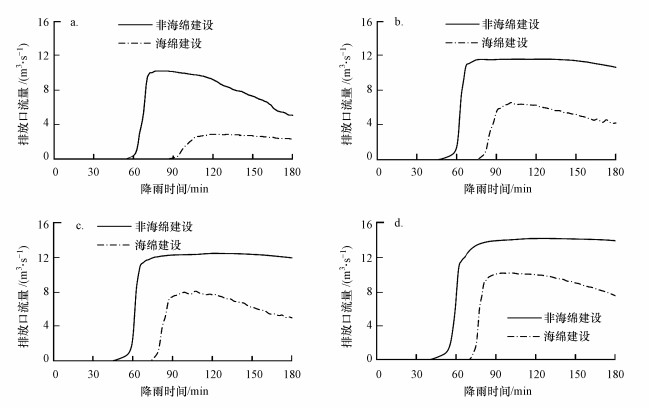 |
| 图 8 不同重现期降雨强度下排放口雨水排放量(a) 1年一遇, (b) 5年一遇, (c) 10年一遇, (d) 50年一遇 Fig. 8 Rainwater discharge of discharge outlet under different rainfall intensity in different recurrence period (a) R1, (b) R5, (c) R10, and (d) R50 |
在2019年全年实际降雨的条件下, 分析两种建设情景下的雨水径流污染物总量, 结果如表 5所示.研究区布设源头减排设施后对雨水径流污染总量削减显著, 全年降雨事件中研究区内总的COD污染物累积削减量23.57 t, 削减率达到32.6%, NH3-N污染物累积削减量3.74 t, 削减率达到37.5%, TP污染物累积削减量0.75 t, 削减率达到34.7%, SS污染物累积削减量421.20 t, 削减率45.9%.结合各子汇水区面积, 分析海绵建设和非海绵建设条件下各子汇水区单位面积污染物贡献量(图 9), 布设源头减排设施的区域, 雨水径流污染物均得到较大程度的削减, 其中, 海绵建设区域的COD、NH3-N、TP和SS污染物削减率分别达到72.2%、69.7%、73.0%和71.3%.
| 表 5 2019年海绵建设前后雨水径流污染物总量 Table 5 Total rainwater runoff pollutants of 2019 |
 |
| 图 9 各汇水区单位面积污染物贡献量(a)海绵建设, (b)非海绵建设 Fig. 9 Contribution of pollutants per unit area in the catchment area (a) Sponge City Construction, (b) Non-sponge city construction |
1) 综合海绵城市源头减排设施建设成本、雨水径流量和污染物控制效率三项关键指标, 提出基于雨水综合径流系数、污染物综合去除率的NSGA-II多目标优化算法, 结合层次分析综合评价方法, 实现目标控制条件下的海绵城市最优化方案设计.
2) 以A中心城区为实际案例, 结合多目标优化-综合分析方法, 提出基于现状条件与规划目标的海绵城市源头减排设施建设方案.建立SWMM排水管网-海绵城市模型, 对研究区海绵城市规划效果进行雨水径流量及径流污染控制的综合分析评价.
3) 海绵城市建设后, 研究区全年雨水下渗量显著增加、蒸发量小幅增加、径流量大幅削减, 雨水年径流总量控制率达到70.1%, 满足研究区海绵城市建设标准.
4) 海绵城市建设能够有效削减雨水径流峰值流量, 在多种设计暴雨场景下, 研究区径流峰值削减率均高于40%, 峰值流量的削减效果随降雨强度增加而减小.对于雨水排放口, 源头减排设施能够充分发挥“渗”、“滞”、“蓄”功能, 削减排放口峰值流量, 大幅延后峰值出现时间, 降低城市内涝风险.
5) 海绵城市建设对雨水面源污染有较好的削减效果, 布设源头减排设施后, 研究区各类雨水径流污染总量显著削减, 其中SS削减效果最佳, 累积削减量421.2 t, 削减率45.9%.此外, 布设源头减排设施的区域, 径流污染物得到更大程度的削减.削减率达70%左右.
Askarizadeh A, Rippy M A, Fletcher T D, et al. 2015. From Rain Tanks to Catchments:Use of Low-Impact Development To Address Hydrologic Symptoms of the Urban Stream Syndrome[J]. Environmental Science & Technology, 49(19): 11264-11280. |
Baek S, Choi D, Jung J, et al. 2015. Optimizing low impact development (LID) for stormwater runoff treatment in urban area, Korea:Experimental and modeling approach[J]. Water Research, 86: 122-131. DOI:10.1016/j.watres.2015.08.038 |
车伍, 赵杨, 李俊奇, 等. 2015. 海绵城市建设指南解读之基本概念与综合目标[J]. 中国给水排水, 31(8): 1-5. |
Deb K, Member A, Ie ee, et al. 2002. A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 6(2): 182-197. DOI:10.1109/4235.996017 |
Eckart K, Mcphee Z, Bolisetti T. 2017. Performance and implementation of low impact development-A review[J]. Science of The Total Environment, 607-608: 413-432. DOI:10.1016/j.scitotenv.2017.06.254 |
符锐, 罗龙洪, 刘俊, 等. 2014. SWMM模型中的低影响开发模块在排水防涝系统中的应用[J]. 水电能源科学, 32(9): 71-74. |
高曼, 池勇志, 赵建海, 等. 2019. 基于边际效益分析的LID设施组合比例研究[J]. 中国给水排水, 35(9): 127-132, 138. |
Garrido-Baserba M, Corominas L, Cortés U, et al. 2020. The Fourth-Revolution in the Water Sector Encounters the Digital Revolution[J]. Environmental Science & Technology, 54(8): 4698-4705. |
郭金玉, 张忠彬, 孙庆云. 2008. 层次分析法的研究与应用[J]. 中国安全科学学报, 18(5): 148-153. |
何爽, 刘俊, 朱嘉祺. 2013. 基于SWMM模型的低影响开发模式雨洪控制利用效果模拟与评估[J]. 水电能源科学, 31(12): 42-45. |
贺文彦, 谢文霞, 赵敏华, 等. 2018. 海绵城市试点区域内面源污染发生过程及其对水体污染负荷贡献评估[J]. 环境科学学报, 38(4): 1586-1597. |
侯精明, 李东来, 王小军, 等. 2019. 建筑小区尺度下LID措施前期条件对径流调控效果影响模拟[J]. 水科学进展, 30(1): 45-55. |
胡爱兵, 任心欣, 丁年, 等. 2015. 基于SWMM的深圳市某区域LID设施布局与优化[J]. 中国给水排水, 31(21): 96-100. |
Jiang Y, Zevenbergen C, Ma Y. 2018. Urban pluvial flooding and stormwater management:A contemporary review of China's challenges and "sponge cities" strategy[J]. Environmental Science & Policy, 80: 132-143. |
刘冬梅, 张弛, 李敏, 等. 2016. 基于多目标优化模型的雨水管网改建[J]. 南水北调与水利科技, 14(3): 183-187, 193. |
Liu H, Gu F, Zhang Q. 2014. Decomposition of a Multiobjective Optimization Problem Into a Number of Simple Multiobjective Subproblems[J]. IEEE Transactions on Evolutionary Computation, 18(3): 450-455. DOI:10.1109/TEVC.2013.2281533 |
马冰然, 曾逸凡, 曾维华, 等. 2019. 气候变化背景下城市应对极端降水的适应性方案研究——以西宁海绵城市试点区为例[J]. 环境科学学报, 39(4): 1361-1370. |
Men H, Lu H, Jiang W, et al. 2020. Mathematical Optimization Method of Low-Impact Development Layout in the Sponge City[J]. Mathematical Problems in Engineering, 2020: 1-17. |
Nguyen T T, Ngo H H, Guo W, et al. 2019. Implementation of a specific urban water management-Sponge City[J]. Science of The Total Environment, 652: 147-162. DOI:10.1016/j.scitotenv.2018.10.168 |
Raei E, Reza Alizadeh M, Reza Nikoo M, et al. 2019. Multi-objective decision-making for green infrastructure planning (LID-BMPs) in urban storm water management under uncertainty[J]. Journal of Hydrology, 579: 124091. DOI:10.1016/j.jhydrol.2019.124091 |
Saadatpour M, Delkhosh F, Afshar A, et al. 2020. Developing a simulation-optimization approach to allocate low impact development practices for managing hydrological alterations in urban watershed[J]. Sustainable Cities and Society, 61: 102334. DOI:10.1016/j.scs.2020.102334 |
陶涛, 肖涛, 王林森, 等. 2019. 海绵城市低影响开发设施多目标优化设计[J]. 同济大学学报(自然科学版), 47(1): 92-96. |
王运涛, 王昊, 王猛, 等. 2020. 基于SWMM的LID改造措施模拟与评估研究[J]. 水资源研究, 9(01): 22-32. |
许萍, 何俊超, 任心欣, 等. 2016. 基于SWMM模型的城市道路LID设施设计参数优化研究[J]. 水电能源科学, 34(2): 21-25. |
杨正, 李俊奇, 王文亮, 等. 2020. 对低影响开发与海绵城市的再认识[J]. 环境工程, 38(4): 10-15, 38. |
俞孔坚, 李迪华, 袁弘, 等. 2015. "海绵城市"理论与实践[J]. 城市规划, 6(39): 26-36. |
赵冬泉, 董鲁燕, 王浩正, 等. 2011. 降雨径流连续模拟参数全局灵敏性分析[J]. 环境科学学报, 31(4): 717-723. |
朱寒松, 董增川, 曲兆松, 等. 2019. 基于SWMM模型的城市工业园区低影响开发效果模拟与评估[J]. 水资源保护, 35(2): 32-36. |
 2020, Vol. 40
2020, Vol. 40


