2019年, 北京市大气污染综合治理取得阶段性进展, 大气环境中PM2.5年均浓度为42 μg·m-3, 创有监测纪录以来新低, 但仍超出国家标准20%;PM10年均浓度为68 μg·m-3, 首次达到国家标准, 但二者仍是北京市出现雾霾天气的主要原因(周涛等, 2012).随着人们的环保意识逐渐加强, 空气质量问题受到了前所未有的重视, 有效快速地模拟出现阶段北京市空气质量状况分布, 可以为下一步的大气环境影响评价、规划、管理和决策等提供依据.
针对大气污染物的时空模拟, 有学者利用遥感反演(赵笑然等, 2017;郝静等, 2018)和模型预测, 如深度学习模型(Pak et al., 2020)、大气数值模拟(孙兆彬等, 2012)、扩散模型(Ciocǎnea et al., 2013)和土地利用回归(Land Use Regression, LUR)模型(Wu et al., 2015;许刚等, 2016;Xu et al., 2019)等方法, 得到了研究区域内污染物的空间分布及变化规律.目前相较其他的模型预测方法, LUR模型可以从影响机制方面解释大气污染物的浓度空间分布, 并且性能通常优于或等于其他的统计方法(如克里金法和离散模型), 已经成为模拟城市尺度大气污染物浓度时空分异最常用的方法之一(Gerard et al., 2008;李杰等, 2017).目前国内已经有学者将LUR模型应用于不同城市的污染物浓度模拟(吴健生等;2015;许刚等, 2016).
有研究表明, 绿色植被对大气环境中的可吸入颗粒物有沉降和消除作用(王嫣然等, 2016).已有的LUR模型中, 尚未有人使用时效性高且获取便捷的植被覆盖度数据.因此, 本文从城市下垫面的异质性出发, 不仅选择了土地覆盖、气象数据(风速、温度、降水等), 还提取了植被覆盖度数据作为自变量, 将PM2.5和PM10浓度作为因变量, 建模方法采用常用的多元线性逐步回归, 并对其进行精度评价和预测, 为北京市大气污染治理提供数据基础及科学依据.
2 数据与方法(Data and methods) 2.1 数据来源与预处理为了获得更加精确的土地覆盖和植被覆盖度数据, 下载了地球探测者网(https://earthexplorer.usgs.gov/) 2019年1—12月(除云雾较多的4月)的Sentinel-2、Landsat8共61景以覆盖整个北京市.Sentinel-2和Landsat8过境时间为北京时间11:00左右, 适合提取植被等地物信息.对影像进行辐射校正等预处理工作, 得到北京市2019年逐月的地表反射率数据.表 1为影像的参数.
| 表 1 影像参数和行列号 Table 1 Parameters and row and column numbers of remote sensing images used in this paper |
对每期影像数据进行镶嵌和裁剪, 并计算其年平均植被覆盖度.植被覆盖度(Vegetation Coverage, VC)的计算使用归一化植被指数NDVI近似估算, 计算公式为在像元二分模型的基础上研究的模型(李苗苗等, 2003):
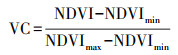
|
(1) |
式中, NDVImin和NDVImax的值分别对应研究区累积概率分布在5%和95%的NDVI值.根据植被覆盖度分类标准, 将得到的VC值进行重分类, 大于0.6为高覆盖, 0.3~0.6为中覆盖, 0.1~0.3为低覆盖, 小于0.1为无覆盖区域.
2019年1—12月北京市PM2.5和PM10逐小时浓度数据, 来自北京市环境保护监测中心网站(http://www.bjmemc.com.cn).北京市共有35个空气质量监测站点, 但植物园监测站点全年数据缺失, 故本文选取剩余34个站点的测量值, 汇总得到各个站点的年均值.34个监测站点按照监测职能分为城区环境评价点11个、郊区环境评价点10个, 对照点及区域点7个以及交通污染监控点5个.其分布状况如图 1所示.
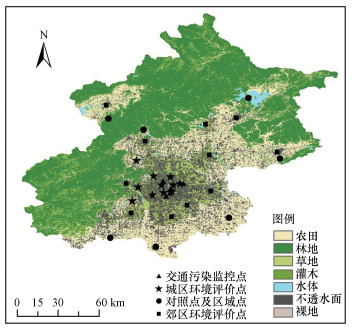 |
| 图 1 北京市土地覆盖和空气质量监测站点分布情况 Fig. 1 Land cover and the distribution of air quality monitoring sites in Beijing |
研究所用到的北京市的土地覆盖数据, 来自清华大学宫鹏教授团队基于Sentinel-2影像绘制的2017年全球土地覆盖数据产品(Gong et al., 2017), 空间分辨率为10 m.基于北京市土地覆盖的具体情况, 将北京市土地覆盖分为:农田、林地、草地、灌木、水体、不透水面、裸地共7类, 并结合2019年的遥感影像, 对研究区土地覆盖类型的变更之处作出修改.
年均风速、温度和降水数据来自中国气象科学数据中心, 用到北京市(18个)及周边(河北15个、天津3个)共36个站点的气象数据, 时间跨度为2019年1月1日—12月31日, 去除其中的缺失值和异常值之后, 求三者的年平均.选择克里金插值的方法, 对34个空气质量监测站点的年均值进行插值模拟.
2.2 研究方法LUR建模的理论依据, 是大气污染物的空间分布与土地利用等地理空间要素存在相关性, 利用地面检测数据和监测点一定范围内地理空间要素构建回归方程, 进而将回归关系推演至未监测地区, 模拟出污染物空间分布.城市范围内监测站点应选取20~80个(Xavier et al., 2012;de Hoogh et al., 2013).步骤为:提取预测变量、建立多元逐步回归模型、模型验证和回归映射.
2.2.1 提取预测变量为了获得与PM2.5和PM10相关性最强的空间尺度, 本文参考了(Henderson et al., 2007;Ross et al., 2012;Wang et al., 2012)的缓冲区设置, 对34个环境空气质量评价站点建立半径为5、3、2、1、0.5、0.3和0.1 km共7个尺度的缓冲区.用缓冲区的矢量文件对年平均植被覆盖度和土地覆盖的栅格数据进行裁剪, 并利用Arcgis的空间分析功能, 得到34个监测站点周围7个尺度缓冲区内的高、中、低3种植被覆盖度和7种土地覆盖类型的面积, 得到自变量70个(7×7+3×7).由于风速、温度和降水数据均以监测点所在位置的插值数据来表示, 所以不对其进行缓冲区分析.综上, 共计准备自变量73个.根据初步经验(Beelen et al., 2013), 将各变量对PM2.5和PM10的影响做出先验假设(表 2).
| 表 2 模型变量系数符号假定 Table 2 Symbol assumption of the variables coefficient |
采用皮尔森相关系数(Pearson correlation coefficient)将每个自变量与PM2.5和PM10的年均浓度进行双变量相关分析, 见式(2).
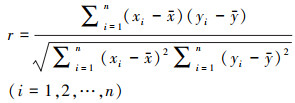
|
(2) |
式中, n为样本量, xi和yi为n个数据的观测值, x和y为n个数据的平均值, 相关系数r的取值范围为(-1, 1), 即|r|越接近1, 则表明x和y的相关程度越高.一般情况下, |r|≥0.8时, 可视为高度相关, 0.5≤|r| < 0.8时, 可视为中度相关;0.3≤|r| < 0.5时, 可视为低度相关;|r| < 0.3时, 说明两个变量之间线性相关性极弱, 可视为非线性相关.
2.2.2 构建模型为了减少属于同一类别的变量之间共线的可能性和保证模型参数的可解释性, 本文参考(Henderson et al., 2007;Wu et al., 2014)的模型构建方法, 先剔除变量与PM2.5和PM10的正负相关性与先验假定不一致的变量;然后筛选出每个子类别中与PM2.5和PM10相关性最高的变量(如5 km范围内林地的面积), 剔除同类因子中与其显著相关(r>0.6)的子变量(如3 km范围内林地的面积);最后将剩余变量代入Stepwise线性回归中, 得到多元线性回归方程, 即研究区的PM2.5和PM10的LUR模型, 形式如下:

|
(3) |
式中, c为污染物预测浓度, αi为待定系数, Xi为自变量, 与每个站点周围的预测变量有关, ε为随机变量.
2.2.3 模型验证与回归映射LUR模型的检验方法主要有Houldout Validation(Wang et al., 2007)、K折交叉验证(Eric et al., 2007)和留一交叉验证(Leave-One-Out Cross Validation, LOOCV) (Gerard et al., 2007).本文由于监测站点数量的限制, 采用留一交叉验证的方法对模型精度进行评估, 即将34个站点分为实验集(33个)和验证集(1个)两部分, 建立LUR模型, 计算出剩余一个样本的模型估计值, 并于该样本点实际的PM2.5和PM10浓度进行比较, 此过程重复34次, 得到研究区LUR模型的模拟精度和均方根误差(LOO-RMSE)即为检验模型好坏的程度的结果.
得到最终的LUR模型后, 利用回归方程对非监测点位的污染物浓度进行模拟, 此过程称为回归映射(Regression Mapping)(Kingham et al., 2000), 该方法比空间插值能更好地从机理上模拟污染物的空间分异.为了预测北京市PM2.5和PM10浓度空间分布, 本文建立了1 km×1 km的规则格点(共14356个), 为每个格点计算回归方程中各预测变量的数值, 代入回归方程得到每个格点的PM2.5和PM10的浓度值, 再将格点的浓度值赋值给格网, 得到研究区PM2.5和PM10浓度的空间分布.
3 结果与分析(Results and analysis) 3.1 PM2.5和PM10浓度统计根据34个监测站点2019年1月1日—12月31日的日均PM2.5浓度数据, 计算其年内变化趋势(图 2)和各个站点年均浓度分布(图 3).
 |
| 图 2 2019年PM2.5和PM10月均浓度值变化 Fig. 2 Changing trend of monthly PM2.5 and PM10 concentration in 2019 |
 |
| 图 3 各监测站点(按方位排列) PM2.5和PM10年均浓度 Fig. 3 Annual average concentration of PM2.5 and PM10 at each monitoring site (arranged by directions) |
经计算可知, 2019年北京市年平均PM2.5浓度42 μg·m-3, 仍超出国家标准20%, PM10年平均浓度为68 μg·m-3, 首次达到国家环境空气质量二级标准.图 2显示, PM2.5的浓度在1月份最高, 达到57 μg·m-3, 随后逐渐呈波动下降的趋势, 在8月份达到最小值, 为23 μg·m-3, 整体规律为秋冬高、春夏低, 波动较为明显;PM10的浓度在1月、4月和11月分别达到85、94和80 μg·m-3 3次峰值, 8月份达到最低值37 μg·m-3, 整体变化规律为冬季和春季较高, 夏季较低, 秋季逐渐上升, 随季节更替波动幅度很大.
图 3中, 横坐标为北京市空气质量监测站点, 从市区(四环内)向远郊按方位排列.可以看出, PM2.5和PM10的浓度在市区较一致, 向西(门头沟)、西北(八达岭)、东偏北(平谷)、东北(密云水库)方向逐渐降低, 向西南(琉璃河)、南(榆垡)、东南(永乐店)方向逐渐升高.PM2.5浓度的最小值出现在西北方向, 定陵附近, 最大值出现在南方, 榆垡附近;PM10浓度的最小值出现在东北方向, 密云水库附近, 最大值出现在西南方向, 琉璃河附近.
3.2 双变量相关分析本研究利用双变量相关分析功能, 带入73个影响因子与各监测站点的年均PM2.5和PM10值, 得到相关系数, 由于预测变量太多, 这里只列出满足t检验的变量.
表 3显示, 与PM2.5浓度相关性大于0.6的, 是0.3 km和0.1 km范围内低植被覆盖的面积和年均风速.与PM10浓度相关性大于0.6的, 是3 km中覆盖的面积和年均风速.从表 4和表 5可以看出, 每个子类别中, 与PM2.5相关性最高的是2 km范围内的耕地面积、5 km范围内的林地面积、1 km范围内水体面积、0.1 km范围内不透水面的面积、0.1 km内低覆盖面积、1 km内中覆盖的面积, 以及每个监测站点的年均风速、温度和降水量.每个子类别中与量PM10相关性最高的是5 km范围内林地面积、2 km范围内水体面积、0.1 km范围内不透水面的面积、0.1 km低覆盖面积、3 km中覆盖面积以及年均风速、温度和降水量.
| 表 3 预测变量与污染物浓度的相关性 Table 3 Correlation between prediction variables and pollutant concentration |
| 表 4 每个子类中与PM2.5相关性最强的变量 Table 4 Variable most strongly associate with PM2.5 in each subclass |
| 表 5 每个子类中与PM10相关性最强的变量 Table 5 Variable most strongly associate with PM10 in each subclass |
深入挖掘不同尺度的对比分析发现:①以PM2.5为例, 当模型系数符号先验假定为负, 即抑制PM2.5浓度的变量(如林地和水体的面积), 林地的对其的抑制能力随着空间尺度增加而增强;水体的抑制力为随空间尺度增加先增强后减弱(注:可能因为北京地区大面积的水体只有密云水库一处, 故此规律不符合常理, 但水体变量并未进入两个回归模型中, 故不做过多探讨). ②当模型系数符号先验假定为正, 即使PM2.5浓度增加的变量(如不透水面和低植被覆盖的面积), 规律则为随着空间范围缩小而影响力增强.
根据模型设置, 剔除与模型先验假设不一致的变量和各子类别中与最高变量的相关性大于0.6的变量, 结果如表 6、表 7所示.
| 表 6 PM2.5模型算法剔除的变量 Table 6 Variables excluded by PM2.5 model |
| 表 7 PM10模型算法剔除的变量 Table 7 Variables excluded by PM10 model |
经过相关分析, 剩余的自变量代入多元线性逐步回归中, 得到PM2.5和PM10的土地利用回归模型, 该模型逐渐向方程中加入变量并剔除不相关的变量, 直到对模型R2的贡献小于1%.模型结果如表 8和表 9所示.
| 表 8 PM2.5逐步多元线性回归结果 Table 8 The results of PM2.5 stepwise multiple linear regression |
| 表 9 PM10逐步多元线性回归结果 Table 9 The results of PM10 stepwise multiple linear regression |
由表 8可知, 研究区PM2.5的LUR模型为(CPM2.5表示PM2.5的浓度):

|
(4) |
由表 9可知, 研究区PM10的LUR模型为(CPM10表示PM10的浓度):

|
(5) |
由表 8和表 9可知, 气象要素是制约污染物在大气中稀释、扩散、迁移和转化的重要因素(李小飞等, 2012).在控制其他因素不变的情况下, 年均风速的增加或减少对PM2.5和PM10的浓度的影响最大, 这是因为风速可以控制污染物的水平分布, 在一定范围内, 风速矢量上升的过程也是污染物浓度下降的过程(周天雄等, 2017).式(4)(5)中, 年均风速每增加0.1个单位, PM2.5和PM10的浓度分别减少10.29和4.29个单位, 风速越大, 越有利于颗粒物的扩散.在式(4)中, 温度是影响PM2.5浓度的又一重要因素, 大气污染物在垂直方向上的扩散主要取决于气温的垂直分布(陈添等, 2006;杨勇杰等, 2006), 随着地表温度升高, 在热力对流的作用下, 土壤扬尘和工业废气、汽车尾气等更容易在空气中扩散, 导致PM2.5浓度增加(蒋雷敏等, 2014).此外, 一定范围内的中等植被覆盖、耕地和不透水面的面积、年均降水量也进入了回归方程中, 共同增加了模型的精度.在式(5)中, 3 km范围内中等植被覆盖的面积也作为预测变量进入了模型中.
综上, 北京市PM2.5和PM10的浓度受全年天气系统的影响居主要地位.但是值得注意的是, 植被覆盖度这一因素不仅进入了上述两个方程, 且影响力都强于其他土地利用类型.对比遥感影像发现, 中等植被覆盖的区域在城区和平原中, 主要是较为密集的草坪、道路两旁的绿化带、行道树、施工裸地中高比例苫盖的部分、居民区人工绿化部分等;在郊区和山地中, 主要是低矮的作物和田间道路等, 这些区域是人类主要活动和干预最剧烈的地方, 水土保持能力较差, 易起扬尘, 导致局部PM2.5和PM10含量增多, 空气质量下降.
3.4 模型验证从表 8和表 9中得知, 两个回归方程F检验方差分析的显著性水平均小于0.01, 说明方程高度显著, 即进入方程的预测变量和污染物浓度之间的线性关系是非常密切的.从调整R2来看, 两个模型所能解释因变量的百分比分别为82.9%和67.7%, 模型的拟合程度较好.
LUR模型的留一交叉验证散点图(图 4).
 |
| 图 4 监测值-预测值散点图(a.PM2.5, b.PM10) Fig. 4 Scatter diagram of monitoring value and predicted value(a.PM2.5, b.PM10) |
图 4显示, 整体上, LUR模型的模拟精度达到0.8452(PM2.5)、0.6626(PM10).对于模型的留一交叉检验(Leave-One-Out Cross Validation, LOOCV), PM2.5和PM10模型的均方根误差(LOO-RMSE)分别为5.61 μg·m-3和7.66 μg·m-3;相对误差分别为4.46%和6.12%.
将本文两模型的修正R2、相对误差和均方根误差等因素与国内外类似研究相对比, 如表 10所示.与相同研究区结果对比表明, 模型的解释精度高、相对误差和留一交叉验证的均方根误差较小;与不同研究区的研究结果相比, 解释精度相当, 但模型变量获取简单, 效率高.本研究中PM2.5模型的调整R2、均方根误差和相对误差在已有研究中表现较好, 但PM10模型的调整R2较低, 均方根误差偏大, 这可能是由于北京市空气质量监测站点分布不均匀, 分布于市中心交通密集区的监测点较密集, 而远郊和山区的监测站点少, 导致的PM10浓度预测存在偏差.对比相同研究区的(Wu et al., 2014;许刚等, 2016)的PM2.5模型研究结果, 本研究的各项指标均有了提高, 这是由于PM2.5浓度在逐年下降, 北京市迁出、关停污染企业、机动车能源结构调整等措施取得的阶段性进展.
| 表 10 土地利用回归模型结果对比 Table 10 Comparison of Land Use Regression model results |
在研究区生成1 km×1 km规则格网和格点, 利用回归方程(4)和(5), 为每一格点计算LUR模型中预测变量的数值, 再将格点的数值赋给对应的格网, 最终得到生成北京市2019年PM2.5和PM10的浓度分布(图 5).
 |
| 图 5 PM2.5和PM10浓度空间分布图(a.PM2.5, b.PM10) Fig. 5 Spatial distribution of PM2.5 and PM10 concentration(a.PM2.5, b.PM10) |
图 5显示, PM2.5和PM10的浓度呈现显著的空间异质性, PM2.5和PM10在西北部山区浓度较低, 高浓度分布区域集中于南偏东的城区和平原地区, 并且有逐渐增加趋势.PM2.5和PM10在平原内部浓度分布不均匀, 其高浓度富集区不仅集中于主城区, 周边郊区尤其是南部的浓度甚至还要高于主城区.产生这个现象的原因可能与地形、气象因素和PM2.5的区域传输有关(Zhang et al., 2013), 也与下垫面不同的植被覆盖度和土地利用类型有一定关系, 在中低植被覆盖区域, 人类活动剧烈, 机动车的行驶、施工裸地的中低苫盖率以及扬尘等都会增加PM2.5和PM10的浓度.
4 讨论(Discussion)由于监测站点数目的限制, 模型只选取了34个监测站点的样本数据, Hoek等(2008)指出, 已有土地利用回归模型的研究中监测站点数的范围为20~100个, 而较为理想的站点个数为40~80个.相比较已有的研究, 本文选取的站点数略少, 这一定程度上限制了模型的精度.此外, 本文无法精确模拟出PM2.5和PM10的日际和季节变化特征, 这可能是由于本文顾及模拟的时效性, 未引入2019年的统计年鉴(尚未出版)中的社会经济数据作为模型变量.而且, 对预测变量求年平均, 能更好地中和其误差, 故本文的模型更适合用于模拟污染物年平均浓度的空间分布.在未来的研究中, 可通过进一步挖掘更为合适的预测变量以及引入时间虚拟变量和时段组合(Dons et al., 2013)的方法来模拟北京市大气污染物的时空分异特征.
5 结论(Conclusions)1) 2019年北京市PM10年平均浓度68 μg·m-3首次达标, PM2.5年平均浓度42 μg·m-3, 仍超出国家标准20%.PM2.5浓度的最小值出现在西北方向, 最大值出现在南方, 年内变化规律为秋冬高、春夏低, 波动较为明显.PM10浓度的最小值出现在东北方向, 最大值出现在西南方, 年内变化规律为冬季和春季较高, 夏季较低, 秋季逐渐上升, 随季节更替波动幅度很大.
2) PM2.5的LUR模型包含的自变量有年均风速、年均温度、1 km范围内中等植被覆盖、2 km范围内耕地和0.1 km范围内不透水面的面积以及年均降水量;PM10模型包含的自变量有年均风速、和3km范围内中等植被覆盖的面积.从调整R2可知, 两个模型所能解释因变量的百分比分别为82.9%和67.7%.
3) 当模型系数符号先验假定为负, 即抑制PM2.5浓度的变量(如林地的面积), 抑制能力随着空间尺度增加而抑制能力增强;当模型系数符号先验假定为正, 即促进PM2.5浓度的变量(如不透水面和低植被覆盖的面积), 促进能力随着空间范围缩小而促进作用增强.
4) 植被覆盖度这一因素不仅进入了两个方程, 且影响力都强于其他土地利用类型.植被覆盖度的数据时效性高, 相比于社会经济数据而言更容易获得, 且成本低廉, 故在以后的PM2.5和PM10的浓度预测中, 可以引入研究区植被覆盖度的数据.
5) PM2.5和PM10的浓度空间分布整体呈现出“西北低, 东南高”的特点, 但在平原内部, 其浓度分布不均匀, 这与气象因素和下垫面的植被覆盖有关.在中低植被覆盖区域, 人类活动剧烈, 机动车的行驶、施工裸地中低苫盖率以及扬尘等都会增加PM2.5和PM10的浓度.
Basagaña X, Rivera M, Aguilera I, et al. 2012. Effect of the number of measurement sites on land use regression models in estimating local air pollution[J]. Atmospheric Environment, 54: 634-642. |
Beelen R, Hoek G, Vienneau D, et al. 2013. Development of NO2 and NOx land use regression models for estimating air pollution exposure in 36 study areas in Europe-the ESCAPE project[J]. Atmospheric Environment, 73: 10-23. |
陈添. 2006. 气象条件对北京市空气质量的影响[J]. 环境保护, 5(10): 46-49. |
Ciocǎnea A, Dragomirescu A. 2013. Modular ventilation with twin air curtains for reducing dispersed pollution[J]. Tunnelling and Underground Space Technology, 37: 180-198. |
de Hoogh K, Wang M, Adam M, et al. 2013. Development of land use regression models for particle composition in twenty study areas in Europe[J]. Environmental Science & Technology, 47(11): 5778-5786. |
Dons E, Van Poppel M, Kochan B, et al. 2013. Modeling temporal and spatial variability of traffic-related air pollution:Hourly land use regression models for black carbon[J]. Atmospheric Environment, 74: 237-246. DOI:10.1016/j.atmosenv.2013.03.050 |
郝静, 孙成, 郭兴宇, 等. 2018. 京津冀内陆平原区PM2.5浓度时空变化定量模拟[J]. 环境科学, 39(4): 1455-1465. |
Henderson S B, Beckerman B, Jerrett M, et al. 2007. Application of land use regression to estimate long-term concentrations of traffic-related nitrogen oxides and fine particulate matter[J]. Environmental Science & Technology, 41(7): 2422-2428. |
Hoek G, Beelen R, De Hoogh K, et al. 2008. A review of land-use regression models to assess spatial variation of outdoor air pollution[J]. Atmospheric Environment, 42(33): 7561-7578. |
蒋雷敏, 李佶. 2014. 天气因数对PM2.5浓度的影响[J]. 科技视界, (29): 125-125. |
Kingham S, Briggs D, Elliott P, et al. 2000. Spatial variations in the concentrations of traffic-related pollutants in indoor and outdoor air in Huddersfield, England[J]. Atmospheric Environment, 34(6): 905-916. DOI:10.1016/S1352-2310(99)00321-0 |
Lee M, Brauer M, Wong P, et al. 2017. Land use regression modelling of air pollution in high density high rise cities:A case study in Hong Kong[J]. Science of the Total Environment, 592: 306-315. DOI:10.1016/j.scitotenv.2017.03.094 |
李杰. 2017.基于LUR模型的武汉市空气质量时空特征分析及模拟[D].武汉: 华中师范大学
|
李苗苗. 2003.植被覆盖度的遥感估算方法研究[D].北京: 中国科学院研究生院(遥感应用研究所)
|
李小飞, 张明军, 王圣杰, 等. 2012. 中国空气污染指数变化特征及影响因素分析[J]. 环境科学, 33(6): 1936-1943. |
Novotny E V, Bechle M J, Millet D B, et al. 2011. National satellite-based land-use regression:NO2 in the United States[J]. Environmental Science & Technology, 45(10): 4407-4414. |
Pak U, Ma J, Ryu U, et al. 2020. Deep learning-based PM2.5 prediction considering the spatiotemporal correlations:A case study of Beijing, China[J]. Science of the Total Environment, 699: 133561. |
潘竟虎, 张文, 李俊峰, 等. 2014. 中国大范围雾霾期间主要城市空气污染物分布特征[J]. 生态学杂志, 33(12): 3423-3431. |
Ross Z, Jerrett M, Ito K, et al. 2007. A land use regression for predicting fine particulate matter concentrations in the New York City region[J]. Atmospheric Environment, 41(11): 2255-2269. DOI:10.1016/j.atmosenv.2006.11.012 |
孙兆彬, 安兴琴, 陶燕, 等. 2012. 基于GIS和大气数值模拟技术评估PM10的人群暴露水平[J]. 中国环境科学, 32(10): 1753-1757. |
Wang M, Beelen R, Bellander T, et al. 2014. Performance of multi-city land use regression models for nitrogen dioxide and fine particles[J]. Environmental Health Perspectives, 122(8): 843-849. DOI:10.1289/ehp.1307271 |
王嫣然, 张学霞, 赵静瑶, 等. 2016. 2013-2014年北京地区PM2.5时空分布规律及其与植被覆盖度关系的研究[J]. 生态环境学报, 25(1): 103-111. |
Wu J, Li J, Peng J, et al. 2015. Applying land use regression model to estimate spatial variation of PM2.5 in Beijing, China[J]. Environmental Science and Pollution Research, 22(9): 7045-7061. DOI:10.1007/s11356-014-3893-5 |
吴健生, 廖星, 彭建, 等. 2015. 重庆市PM2.5浓度空间分异模拟及影响因子[J]. 环境科学, 36(3): 759-767. |
许刚, 焦利民, 肖丰涛, 等. 2016. 土地利用回归模型模拟京津冀PM2.5浓度空间分布[J]. 干旱区资源与环境, 30(10): 116-120. |
Xu H, Bechle M J, Wang M, et al. 2019. National PM2.5 and NO2 exposure models for China based on land use regression, satellite measurements, and universal kriging[J]. Science of the Total Environment, 655: 423-433. DOI:10.1016/j.scitotenv.2018.11.125 |
杨勇杰, 谈建国, 郑有飞, 等. 2006. 上海市近15a大气稳定度和混合层厚度的研究[J]. 气象科学, (5): 536-541. |
Zhang A, Qi Q, Jiang L, et al. 2013. Population exposure to PM2.5 in the urban area of Beijing[J]. PloS one, 8(5): 63486. |
赵笑然, 石汉青, 杨平吕, 等. 2017. NPP卫星VIIRS微光资料反演夜间PM2.5质量浓度[J]. 遥感学报, 21(2): 291-299. |
周涛, 汝小龙. 2012. 北京市雾霾天气成因及治理措施研究[J]. 华北电力大学学报(社会科学版), (2): 12-16. |
周天雄, 王国强, 匡汉祎, 等. 2017. 常州市PM2.5与风向风速关系分析[J]. 农业与技术, 37(9): 140-141. |
 2020, Vol. 40
2020, Vol. 40


