2. 南京大学大气科学学院, 南京 210023;
3. 重庆市气象台, 重庆 401147;
4. 重庆市环境科学研究院, 重庆 401147
2. School of Atmospheric Sciences, Nanjing University, Nanjing 210023;
3. Chongqing Meteorological Observatory, Chongqing 401147;
4. Chongqing Institute of Environmental Science, Chongqing 401147
生态文明建设、公众健康保障及城市交通运行等对大气环境提出了更多、更高的要求, 当前人们对健康环境的需求也越来越迫切(Xie et al., 2016a;2016b;2017;Zhao et al., 2018).近年来, 颗粒物成为我国许多城市和地区的首要污染物, 较高的颗粒物浓度会危害人类健康, 降低能见度, 并对公众的生命和财产安全造成威胁(Cai et al., 2018;Zhan et al., 2019), 因此, 开展准确的空气质量预报工作十分必要.过去依据经验和统计的预报方法在理论和时效性等方面无法满足现今的需求, 近年来气象模式和大气化学模式相结合的数值预报系统研究迅速发展, 并以其完善的理论基础、模式设计、定时定量、高分辨率时效性等优势成为区域空气质量预报的发展趋势.目前, 由美国环保署开发并推荐的第三代空气质量模式, 其核心为CMAQ模式, 经过数十年的发展, 融入了许多当前大气化学和物理领域的最新研究成果.国内外的科研与应用成果表明, CMAQ模式对多种污染物的时空分布及变化趋势具有较强的预报能力, 以其多尺度、灵活性等优点, 成为国内外区域和城市空气质量预报中应用最为广泛的模拟系统之一, 并用于管控效果评估决策和污染传输沉降分析研究, 取得了较好的效果(唐孝炎等, 2006;王茜等, 2015;程兴宏等, 2016;吴钲等, 2018).
目前, 由于多种原因, 如排放源清单的不确定性较大, 模式的物理、化学机制极为复杂, 以及物理过程参数化仍需不断完善等, 导致空气质量模式对于主要污染物的预报误差较大, 因此, 需要对模式预报结果进行客观订正, 以提高预报结果的准确性(程兴宏等, 2016;汤静等, 2019).近年来, 对于空气质量预报模式的订正也取得了长足的发展, 例如, 针对应用普遍的CMAQ模式, 国内诸多研究分别采用多元线性逐步回归、PCA-kNN、偏最小二乘回归、多层递阶等一系列方法对模式结果进行了订正, 发现订正后的结果可以明显降低污染源不确定性造成的模式模拟误差(王茜等, 2015;杨关盈等, 2017;吕梦瑶等, 2018;张岳军等, 2018;李颖若等, 2019).上述研究通过引入历史实测和预报数据对模式预报结果进行修订是可行的.此后, 又有学者引入气象条件并研究其对大气污染物传输、扩散和转化的影响, 结果显示, 风速、气温、相对湿度等气象因子与污染物浓度存在显著相关性, 因此, 又有部分学者尝试引入动力-统计订正模型, 并取得了一定的订正效果.机器学习方法可以有效地捕捉大气成分变化中隐藏的非线性特征, 通过处理海量数据, 更客观、灵活地构建模型, 从而在预报中表现出良好的性能, 但在目前的空气质量预报相关文献中却应用较少(孙全德等, 2019;门晓磊等, 2019).
成渝地区位于我国西南部, 涵盖了四川省东部的大部分城市和重庆市, 是我国人口最集中且周边地势起伏最大的城市群区域.该区域汽车保有量大, 工业发达, 加之近年来地区经济发展迅速, 导致污染物排放量大.区域地形是盆地, 四面环山, 地形闭塞, 年平均风速较小, 不利于污染物的输送扩散, 且盆地内江河纵横, 水汽充沛, 常年处于高湿条件下, 容易形成污染和低能见度天气.目前, 成渝地区已成为我国四大大气污染事件高发地之一(Cai et al., 2016;Zhao et al., 2018).过去, 成渝地区空气污染的主要类型为SO2和PM10, 随着相关治理措施的实施, 当前的污染类型主要表现为细颗粒物污染(Tian et al., 2017;Wang et al., 2018).因此, 开展该区域高分辨率空气质量数值预报的研究十分必要.重庆市气象局基于现有的数值天气预报系统(SSRAFS)开展了本地化的环境气象数值预报系统建设, 引入CMAQ模式进行本地化研究, 为污染天气的预报提供了良好的技术支撑和一定的参考价值.
基于此, 本文采用机器学习方法(Lasso回归、随机森林回归和深度学习RNN-LSTM), 对WRF-CMAQ模式预报PM2.5浓度进行订正.根据区域地理和气候特征, 参考文献方法(Zhao et al., 2018)将成渝地区22个城市和自治州划分为4个区域(图 1和表 1), 基于机器学习算法自适应地获得这4个区域相关要素的特征参数, 并进行相关特征要素的选择, 然后以选择的特征集进行机器学习的建模, 对成渝地区PM2.5浓度数值预报结果进行订正, 并通过统计检验和分级检验比较各种订正方法的修正效果.
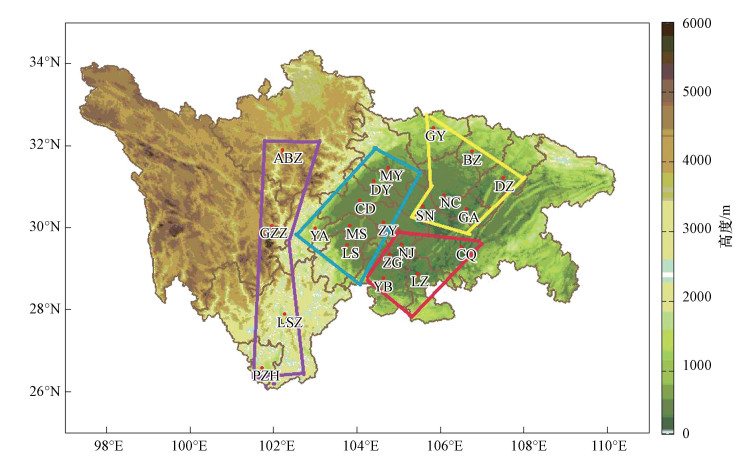 |
| 图 1 成渝地区主要城市及区域划分 Fig. 1 Main cities and four sub-regions in Chengyu region |
| 表 1 成渝地区区域划分 Table 1 Four sub-regions in Chengyu region |
本文使用基于空气质量预报系统WRF-CMAQ的重庆市气象局高分辨率数值预报系统.模式每日8:00起报, 预报未来72 h的污染物浓度, 本文取模式次日0:00—24:00预报值进行相关订正研究, 通过插值得到成渝地区22个大气成分城市监测站点的PM2.5逐时浓度.本研究所使用模式的基本设置如表 2所示.
| 表 2 WRF-CMAQ模式基本设置 Table 2 Key parameters in WRF-CMAQ model |
本文采用2018年污染物实测资料作为标记(机器学习算法中的真值).成渝地区22个城市监测点逐时观测的PM2.5、PM10、O3、SO2、NO2、O3浓度数据来自中国环境监测总站(http://106.37.208.233:20035/).同时期逐小时的地面气象观测资料来自距离22个城市环境监测点最近的自动气象站, 包括气压、温度、露点温度、相对湿度、风向、风速.
提取2018年1月、4月、7月和10月重庆市气象局高分辨率数值预报系统3 km分辨率每日8:00起报的相关气象要素场, 取次日0:00—24:00预报值, 通过临近插值法得到22个大气成分城市监测站点的相关气象和地理要素, 即查找距离站点最近的格点值插值为站点值, 作为机器学习算法的输入, 以此来构建机器学习PM2.5浓度订正模型, 其中, 1月、4月、7月和10月分别代表冬、春、夏和秋季.初步选取的相关气象和地理要素包括地形高度、地表气压、2 m温度、2 m相对湿度、2 m露点温度、10 m纬向风、10 m经向风、850 hPa高度温度、850 hPa垂直速度、700 hPa垂直速度、850 hPa位势涡度、700 hPa位势涡度、850 hPa纬向风、700 hPa纬向风、850 hPa经向风、700 hPa经向风、边界层高度、降水量, 另外参考相关文献, 还引入了前日PM2.5、PM10、SO2、NO2、O3观测浓度, 以及前日气象自动站观测到的气压、温度、露点温度、相对湿度、降水、风向、风速, 共31个变量作为机器学习算法的输入进行模型特征量的选择和模型训练, 以此来订正PM2.5模式预报浓度.
2.2 机器学习算法 2.2.1 Lasso回归Tibshiran(2011)提出的Lasso(Least absolute shrinkage and selection operator)方法, 是一种有偏估计的方法, 可以用来进行高维数据的特征选择.Lasso方法通过构造一个惩罚函数, 压缩一部分系数, 设定一些系数为0, 从而保留子集收缩的优点, 是一种处理具有复共线性数据的有偏估计.
在PM2.5浓度预测中, 首先构造目标函数f(λ):
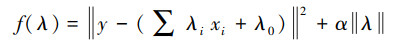
|
(1) |
式中, y为PM2.5实测浓度, xi为自变量特征向量中第i个特征上的取值, (∑λixi+λ0)为通过31个特征量的线性组合预测得到的PM2.5浓度.然后通过对f(λ)求最小值, 求得λi和λ0, 从而确定Lasso回归模型, 求得的解具有一定的稀疏性, 可以实现自变量相关性的选择.
2.2.2 随机森林随机森林(Rondom Forest)是一种基于集成学习思想的统计算法, 通过重抽样方法从原始样本中抽取多个样本, 并对每个样本进行决策树建模, 最后对多个决策树的预测值进行平均得到最终的预测结果.随机森林算法对异常值和噪声具有较好的容忍度, 不容易出现过拟合, 在数据挖掘各个领域具有较广的应用性.
随机森林方法的一般训练过程如下:①构建原始数据集(式(2));②有放回地从数据集中随机抽取子集作为训练数据集Dj, 并使用一种随机子空间划分的策略构建每颗决策树, 从中优选最优特征进行分裂, 重复训练后得到N颗决策树hi, 组成随机森林;③预测结果为每颗决策树的平均.随机森林是多元非线性回归模型, “双随机”的思想使得随机森林不容易陷入过拟合, 并使各分类器之间存在多样性.
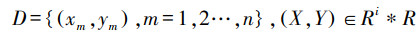
|
(2) |
式中, Y为PM2.5实测浓度, X为自变量.
2.2.3 深度学习循环神经网络RNN(Recurrent Neural Network)是深层神经网络的一种, 可以用来处理时间序列数据.相比普通的深度神经网络DNN(Deep Neural Network), RNN不仅会考虑前一时刻的输入, 同时认为当前输出与前面的输出也有关, 具体表现为网络对前面的信息进行记忆并用于当前输出的计算中.
深度学习由输入层、隐藏层和输出层组成, 隐藏层可以包含多层(图 2).在模型训练中, DNN信息从输入层、隐藏层到输出层是单向流动, 且层与层之间是全连接的, 每层节点间是无连接的, 而RNN通过引入环状结构建立了神经元上一时刻的“记忆”到自身的连接, RNN输入值为x, 计算得到隐藏层状态序列h, 通过反复迭代训练后得到输出序列y, 其中迭代训练公式为:
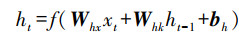
|
(3) |
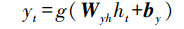
|
(4) |
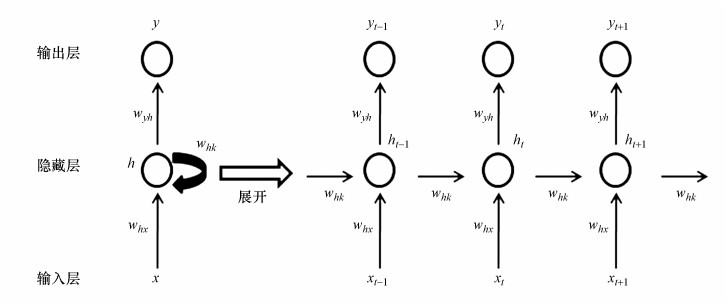 |
| 图 2 循环神经网络基本模型 Fig. 2 The concept of recurrent neural network |
式中, Whx是输入层到隐藏层的权重矩阵, Whk是隐藏层自循环的权重矩阵, Wyh是隐藏层到输出层的权重矩阵;bh和by为隐藏层和输出层的偏差矩阵;f和g为隐藏层和输出层的激活函数.RNN在时间序列的预测中具有比DNN更好的表现.
RNN在反向传播中使用的是BPTT(Back-propagation through time), 将最后一个时间积累的损失传递回来, 进行参数的更新.传统RNN存在梯度消失的问题, 即当前的输出与非常久远的时间序列有关, 导致RNN将无法学习到, 因此, Hochreiter和Schmidhuber提出了LSTM网络(Long short term memory networks).LSTM网络可以通过忘记门、输入门和输出门3个称为门的丢弃结构对细胞状态进行添加或删除信息, 门的结构由一个sigmoid层和一个点乘操作组合, 通过sigmoid层的输出决定能够流过的信息(图 3).
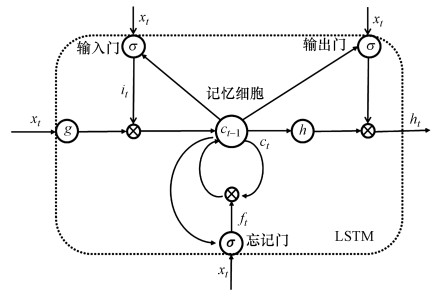 |
| 图 3 LSTM基本模型 Fig. 3 The concept of LSTM |
第一步通过忘记门并根据输入的ht-1和xt判断丢弃的信息, 其中, Wfx、Wfh、Wfc分别为输入、上时刻输出和记忆细胞到忘记门的权重矩阵, bf为忘记门的偏差矩阵, ft为忘记门的输出(式(5));下一步通过输入门决定为细胞状态添加的信息, 其中, Wix、Wih、Wic分别为输入、上时刻输出和记忆细胞到输入门的权重矩阵, bi为输入门的偏差矩阵, it为输入门的输出(式(6)), 并将细胞信息ct-1更新为ct, Wcx、Wch分别为输入、上时刻输出到记忆细胞的权重矩阵, bc为偏差矩阵(式(7));最后经过输出门判断输出的信息, 其中, Wox、Woh、Woc分别为输入、上时刻输出和记忆细胞到输出门的权重矩阵, bo为输出门的偏差矩阵, ot为忘记门的输出(式(8)), 通过输出的激活函数φ得到最终RNN单元的输出ht(式(9)).
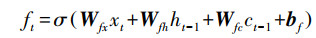
|
(5) |
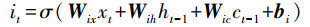
|
(6) |
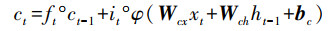
|
(7) |
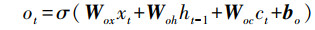
|
(8) |
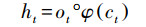
|
(9) |
通过RNN-LSTM构建训练模型订正模式模拟PM2.5浓度, 构建一个输入层、一个LSTM网络层、一个输出层, 输入数据为选择后的特征量矩阵, 隐藏层记忆细胞为10, 激活函数为tanh, 优化器选择Adam算法, 每次训练样本数batch_size根据不同区域训练样本数变化, 学习步长为24, 将整个序列分为20个时间段, 反复迭代训练200次, 将训练后的模型在测试数据上进行验证.
2.2.4 检验方法检验采用统计检验和分级检验, 统计检验选择指标包括平均偏差MB(式(10))、均方根误差RMSE(式(11))和相关系数r(式(12)).平均偏差主要反映了预报值与观测值的平均偏离情况, 均方根误差主要反映预报值与观测值的总体偏离情况, 体现数据的离散程度.
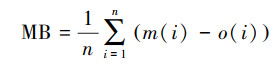
|
(10) |
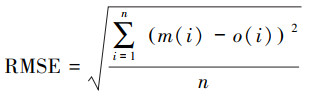
|
(11) |
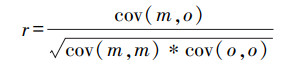
|
(12) |
式中, m(i)为预报值, o(i)为观测值, covm, o为m和o的协方差, cov(m, m)和cov(o, o)为m和o的方差.
3 订正模型构建(Adjusting model construction) 3.1 数据预处理为避免各自变量特征要素量级不同对训练结果的影响, 对数据进行预处理, 剔除数据矩阵中的缺值和乱码, 并对数据进行标准化处理.4个区域的初始数据矩阵, 2018年4个代表月共2952个小时时次, 盆地西、盆地南、盆地东北和西部高原区域分别有20664、14760、17712和11808个样本, 剔除缺值和滑动长度, 4个区域的样本数分别为16894、11980、14120、9486个, 每个样本的自变量特征为31个.
3.2 特征量选择本文基于Lasso回归进行特征量的选择, 随着惩罚力度的加强, 特征量维度逐渐降低, 达到较显著变量的自动选择目的, 该方法属于嵌入式选择法, 即特征选择和学习训练过程在同一个优化过程中完成.
通过Lasso回归训练, 可以得到4个区域各个特征量与PM2.5浓度的权重系统, 按照权重绝对值大小排序, 并针对不同区域使用不同维数的特征量矩阵进行训练.当特征量维度达到一定数量时, 均方根误差达到在一个稳定的水平, 不再显著下降(图 4).特征量优选可以学习任务的难度, 降低计算和存储开销, 并且使得学习模型的可解释性提高.针对不同区域, 盆地西选择13个特征量、盆地南选择10个特征量、盆地东北选择9个特征量、西部高原选择12个特征量进行Lasso回归、随机森林和深度学习的训练.
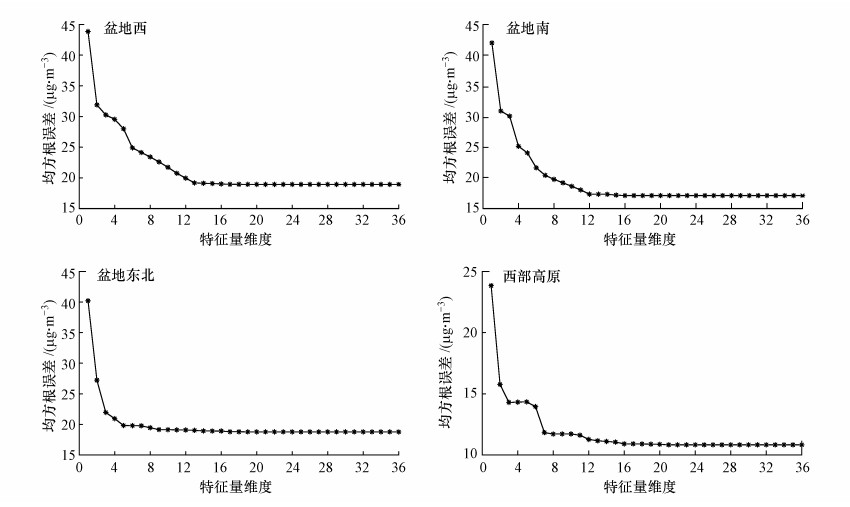 |
| 图 4 基于Lasso回归PM2.5浓度的预测均方根误差 Fig. 4 The root mean squared error between observed PM2.5 concentrations and predicted PM2.5 concentrations based on Lasso regression |
表 3列出了各个区域构建订正模型选择用到的特征量.前人通过综合观测、模拟分析及源解析等多种手段研究表明, 大气中细颗粒物的形成和演化机制中, 硫酸盐、硝酸盐等存在复杂的化学反应(Tian et al., 2017;Chen et al., 2018;Li et al., 2019).因此, PM2.5与前日的大气成分(PM2.5、PM10、SO2、NO2)具有较好的相关性, 不同区域的相关成分又略有不同, 盆地南包括了重庆在内的一些工业较为发达的城市, 因此, 硫化物与颗粒物的相关性较好;而盆地西是以成都为代表的盆地内城市群, 重工业较少, 细颗粒物与硫化物相关性较小.其次, 诸多研究表明, 气象条件对PM2.5的输送和扩散具有不可忽略的作用, 通常地面风速较大时, PM2.5浓度不太容易维持高值, 气象条件对PM2.5的影响更多地体现在天气形势上, 当天气系统发生变化, 如冷空气来袭, 地面温度降低、湿度降低、气压升高, 此时PM2.5浓度通常降低(Li et al., 2016;Zhong et al., 2018;宁贵财, 2018;Zhan et al., 2019).因此, PM2.5浓度与近地面温度、湿度、气压表现出一定的相关性.盆地西、盆地南、盆地东北位于盆地内部, 冷暖气团的交替表现为较为显著的纬向风影响, 部分地区位于盆地边缘, 且西部高原海拔较高, 不仅受到纬向风的影响, 与经向风也具有一定的相关性.另外, PM2.5浓度变化还受到垂直气流的影响, 盆地西表现为850 hPa位涡, 位涡为负表现为下沉气流, 污染物不易扩散, 易导致PM2.5浓度升高;其他区域高相关要素为边界层高度, 通常春季边界层高度较高时, 有利于大气污染物的传输扩散, 秋、冬季边界层高度较低, 易导致PM2.5积聚.
| 表 3 成渝地区各区域特征量选择 Table 3 The selected features for each sub-region in Chengyu region |
将各区域选择出的特征量重新组合为新的自变量矩阵, 为使得训练和测试样本更具有区域代表性及时间代表性, 同时鉴于气象与大气成分观测数据会受到仪器及周边环境的影响, 为避免部分站点观测因客观条件干扰造成的偏差对训练与测试结果产生影响, 并且考虑到神经网络和树模型训练更适用于较大样本量的数据集(Halevy et al., 2009), 为取得足够多的样本数, 故将区域内所有站点和所有时间数据打乱后, 随机抽取85%的数据作为训练集.其中, 盆地西、盆地南、盆地东北、西部高原分别为14360(样本数)×13(特征量)、10183(样本数)×10(特征量)、12002(样本数)×9(特征量)、8063(样本数)×12(特征量)的输入矩阵, 对应的目标矩阵分别为盆地西14360(样本数)×1(PM2.5浓度)、盆地南10183(样本数)×1(PM2.5浓度)、盆地东北12002(样本数)×1(PM2.5浓度)、西部高原8063(样本数)×1(PM2.5浓度).采用机器学习方法(Lasso回归、随机森林回归和深度学习RNN-LSTM)分别使用训练数据集进行模型训练.
测试数据集为另外15%的数据, 其中, 盆地西、盆地南、盆地东北、西部高原分别为2534(样本数)×13(特征量)、1797(样本数)×10(特征量)、2118(样本数)×9(特征量)、1423(样本数)×12(特征量)的输入矩阵, 对应的目标矩阵分别为盆地西2534(样本数)×1(PM2.5浓度)、盆地南1797(样本数)×1(PM2.5浓度)、盆地东北2118(样本数)×1(PM2.5浓度)、西部高原1423(样本数)×1(PM2.5浓度).训练数据集和测试数据集各站点样本数分布情况如图 5所示, 由图可知, 各站点随机抽取数据样本数较为均匀.不同区域各季节的训练和测试样本数分布情况如图 6所示, 由图可知, 各季节随机抽取的样本数较为均匀.因此, 区域训练结果具有空间和时间代表性.使用Lasso回归、随机森林回归和深度学习RNN-LSTM训练所得的模型对测试数据集模式模拟预报结果进行订正, 并对订正结果进行检验分析.
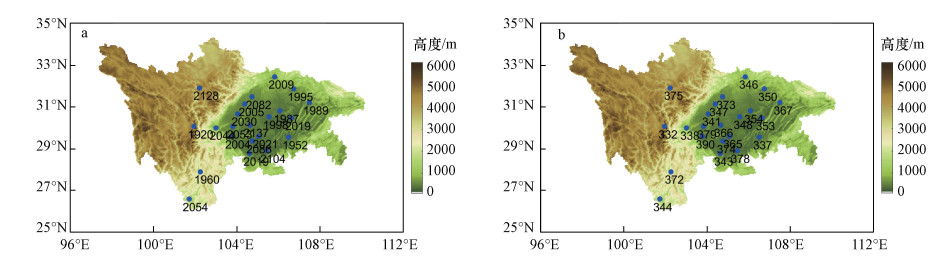 |
| 图 5 训练数据集(a)和测试数据集(b)各站点样本数 Fig. 5 The number of samples in the training (a) and test (b) data set in each site |
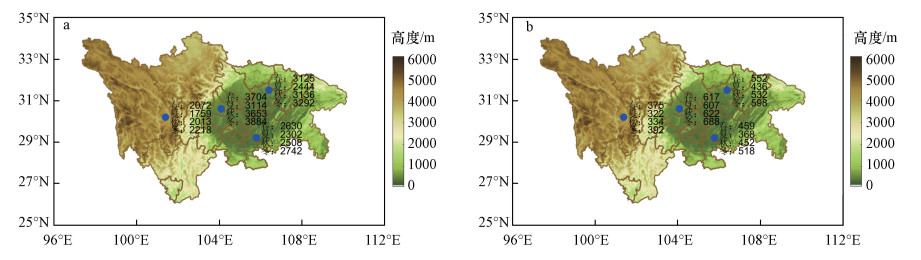 |
| 图 6 训练数据集(a)和测试数据集(b)各季节区域样本数 Fig. 6 The number of samples in the training (a) and test (b) data set in each season of different sub-regions |
对成渝地区22个城市站点PM2.5小时浓度经CMAQ模拟、Lasso回归订正、随机森林回归订正和RNN-LSTM订正后进行统计检验, 分别计算平均误差、均方根误差和相关系数(图 7), 并分别计算各站点基于3种订正方法针对模式订正后误差的改进效果(图 8).从平均偏差来看, 22个站点中, 有2个站点(重庆和成都)的平均偏差偏高, 其余20个站点的平均偏差偏低, 说明成渝地区CMAQ模拟预报普遍低估了PM2.5浓度.这可能是由于排放源与实际情况存在一定的差异(吴钲等, 2018;汤静等, 2019);另外, 模式模拟的近地面风速普遍偏大也是原因之一, 评估结果显示, 22个站点的模拟风速较实测风速平均高1~2 m·s-1, 这与麦健华等(2018)和汤静等(2019)的研究结论相近.CMAQ模拟的PM2.5小时浓度与实测值的平均偏差为-32.64~14.59 μg·m-3, 经过Lasso回归订正后, 22个站点的平均偏差降低至-3.12~4.87 μg·m-3, 其中, 平均偏差绝对值较大的站点位于盆地内, 成都为-3.02 μg·m-3, 自贡为-3.12 μg·m-3和内江为4.87 μg·m-3, 经过随机森林订正后的平均偏差为-1.26~2.62 μg·m-3, 经过RNN-LSTM订正后的平均偏差为-2.97~2.49 μg·m-3;订正后的平均偏差绝对值相比模式模拟更接近0, 偏差明显降低, 其中, 随机森林回归和RNN-LSTM订正后的平均偏差相对Lasso回归降低效果更好.
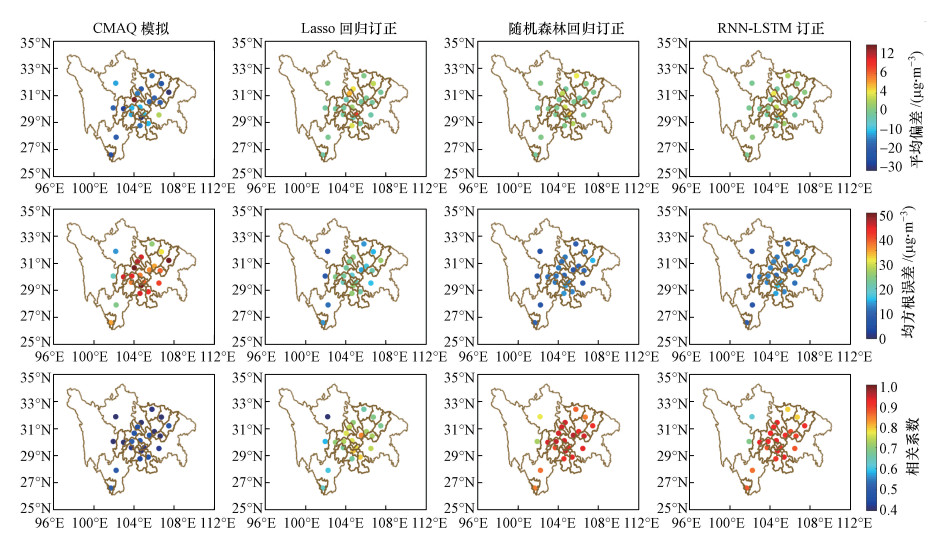 |
| 图 7 成渝地区各站点PM2.5浓度模式预报与订正的平均偏差、均方根误差与相关系数 Fig. 7 The mean bias, root mean squared error and correlation coefficient between the observed PM2.5 concentrations and the predicted PM2.5 concentrations based on the numerical forecasting and three adjusting methods at each site in Chengyu region |
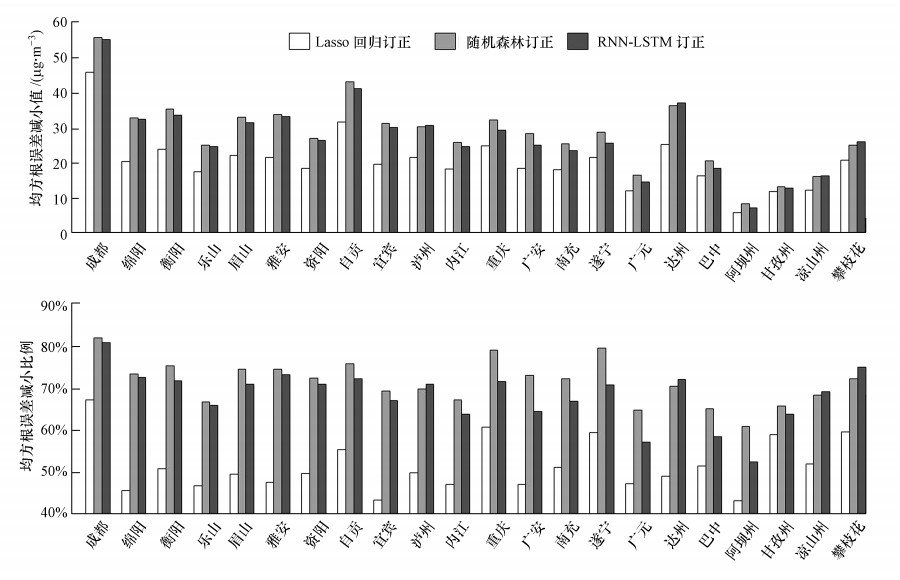 |
| 图 8 成渝地区各站点PM2.5浓度模式订正后均方根误差减小值及减小比例 Fig. 8 The absolute and relative reduction of the root mean squared error between observed and predicted PM2.5 concentrations caused by three adjusting methods at each site in Chengyu region |
其次, 均方根误差检验显示CMAQ模拟的PM2.5小时浓度与实测值的均方根误差为13.49~68.15 μg·m-3, 经过订正后均方根误差显著降低(图 8), 其中, Lasso回归订正后的均方根误差为7.67~26.22 μg·m-3, 随机森林回归订正后的均方根误差为5.26~15.16 μg·m-3, RNN-LSTM订正后的均方根误差为6.42~15.80 μg·m-3.随机森林回归和RNN-LSTM订正后的均方根误差减小值和减小比例大于Lasso回归, 其中, 泸州、达州、凉山州和攀枝花城市站点的PM2.5小时浓度数据经RNN-LSTM订正后均方根减少略高于随机森林回归, 其余18个站点的PM2.5小时浓度数据经随机森林回归订正后均方根减少高于RNN-LSTM.
CMAQ模拟的PM2.5小时浓度与实测值的相关系数为0.31~0.51, Lasso回归订正后的相关系数为0.38~0.83, 其中, 订正后相关系数低于0.65的地区为海拔较高的西部高原上的阿坝州、甘孜州、凉山州和攀枝花, 随机森林回归订正后的相关系数为0.73~0.96, RNN-LSTM订正后的相关系数为0.63~0.93, 随机森林回归和RNN-LSTM订正后的相关系数较低的地区为阿坝州和甘孜州, 其中, 泸州、达州、凉山州和攀枝花站点经RNN-LSTM订正后的相关系数高于随机森林回归, 其他站点经随机森林回归订正后的相关系数高于RNN-LSTM, 这与均方根误差的订正效果一致.总体而言, 站点统计检验表明, 基于3种机器学习方法订正后的PM2.5小时浓度相较CMAQ模式模拟预报结果, 偏差显著降低, 相关系数显著提高, 其中, 随机森林回归和RNN-LSTM的订正效果优于Lasso回归, 而随机森林回归的订正效果又略优于RNN-LSTM, 这可能是因为RNN-LSTM对于连续时间序列的训练结果更为理想, 而随机抽取的训练数据集不具备时间连续性.
4.2 分区域评估表 4给出了2018年成渝地区各区域PM2.5小时浓度经CMAQ模拟及Lasso回归、随机森林回归、RNN-LSTM订正后的平均偏差、均方根误差和相关系数.由表 4可知, CMAQ模式模拟的4个区域PM2.5小时浓度的平均偏差均小于0, 预报值平均低于实测值;基于机器学习订正后的平均显著偏差减小, 更接近0;CMAQ模式预报的盆地西、盆地南和盆地东北3个区域的均方根误差值在40 μg·m-3以上, 西部高原的均方根误差相对较小为23.84 μg·m-3, 并且, 西部高原地区的相关系数较其他3个区域也相对较高.总体而言, CMAQ模式对盆地西、盆地南和盆地东北3个区域的预报水平较为相当, 对西部高原的预报水平相对高一些.采用3种机器学习方法订正后4个区域的PM2.5小时浓度的偏差和相关系数都有显著改善, 其中, Lasso回归订正后的均方根误差减小比例在50%左右, 相关系数在70%以上, 随机森林和RNN-LSTM订正后的均方根误差较小比例在70%左右, 相关系数达90%左右.可知对于4个区域PM2.5小时浓度进行订正, 无论是偏差大小还是变化趋势, 随机森林和RNN-LSTM的订正效果都要优于Lasso回归, 随机森林和RNN-LSTM的订正效果较为相近, 其中, 对于盆地西和盆地东北部, 随机森林的订正效果略优于RNN-LSTM.
| 表 4 成渝地区各区域PM2.5浓度模式预报与订正的平均偏差、均方根误差与相关系数 Table 4 The mean bias, root mean squared error and correlation coefficient between the observed and the predicted PM2.5 concentrations based on the numerical forecasting and three adjusting methods in each sub-regions |
图 9给出了成渝地区2018年4个区域PM2.5浓度预报与订正偏差的概率分布特征.由图可知, CMAQ模拟的PM2.5浓度与实测值的偏差, 以及订正后的浓度偏差均能表现出正态分布的特征.表 5统计了各区域模式模拟及订正偏差的分布范围.由表可知, 盆地西与盆地南的模式预报偏差集中分布在-100~50 μg·m-3, 70%的偏差集中在-70~30 μg·m-3, 盆地东北的偏差集中在-85~25 μg·m-3, 70%的偏差集中在-65~5 μg·m-3, 西部高原的偏差集中在-55~5 μg·m-3, 70%偏差集中在-45~5 μg·m-3, 模式预报的偏差值明显偏向负值, 最大概率分布的范围较宽.经过Lasso回归订正后, 偏差集中在±45 μg·m-3以内, 70%的偏差集中在±20 μg·m-3以内;经过随机森林回归订正后, 偏差集中在±30 μg·m-3以内;经过RNN-LSTM订正后偏差集中在±30 μg·m-3以内, 75%的偏差集中在±15 μg·m-3以内;订正后的偏差集中在0左右, 最大概率分布范围变窄, 明显改善了模式预报PM2.5浓度较低的情况.其中, 随机森林回归与RNN-LSTM订正后的偏差范围相比Lasso回归集中范围更窄, 最大概率分布更集中, 表明订正效果更为显著.
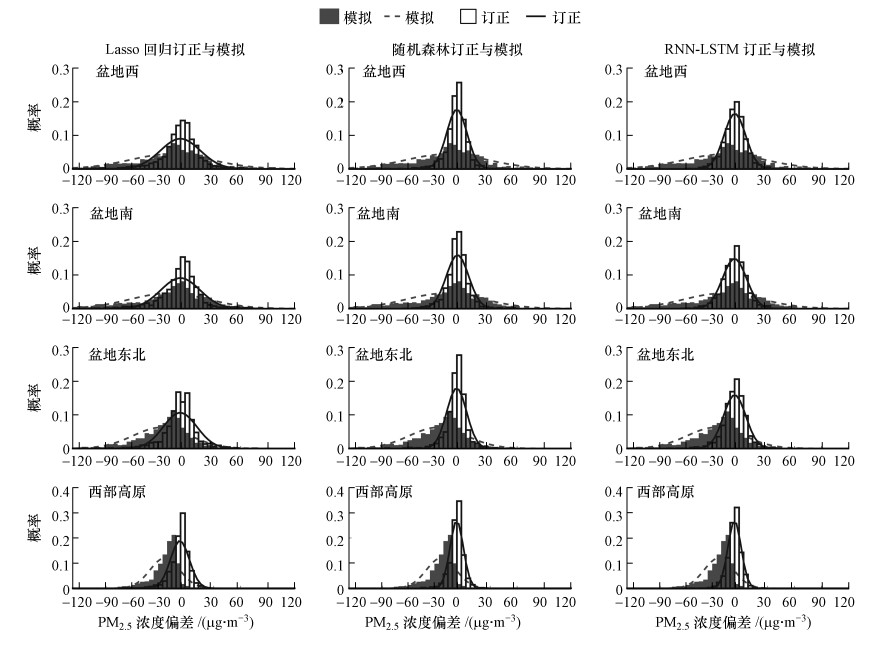 |
| 图 9 成渝地区各区域PM2.5浓度模式预报与订正偏差的概率分布图 Fig. 9 The probability distribution of the deviations between the observed PM2.5 concentrations and the predicted PM2.5 concentrations based on the numerical forecasting and three adjusting methods at each sub-region in Chengyu region |
| 表 5 成渝地区各区域PM2.5浓度模式预报与订正偏差的分布范围 Table 5 The deviation distribution of PM2.5 concentration for the numerical forecasting and three adjusting methods in each sub-regionsμg·m-3 |
图 10给出了成渝地区各区域PM2.5浓度不同季节的模式预报与订正效果, 结合相关系数及均方根误差可知, Lasso回归、随机森林回归、RNN-LSTM 3种订正方法对不同季节及区域的PM2.5模拟结果均可产生一定的订正效果.不同区域四季PM2.5浓度的订正效果整体表现为随机森林回归和RNN-LSTM优于Lasso回归, 随机森林回归又略优于RNN-LSTM.Lasso回归订正结果的相关系数达到0.6~0.7, 均方根误差减小40%~60%, 随机森林订正的相关系数达到0.80~0.95, 均方根误差较小60%~80%, RNN-LSTM对4个区域冬季的订正效果较好, 相关系数达到0.9以上, 均方根误差减小70%以上, 对夏季的订正效果差于随机森林回归, 可能是由于受到样本数的影响(Halevy et al., 2009).
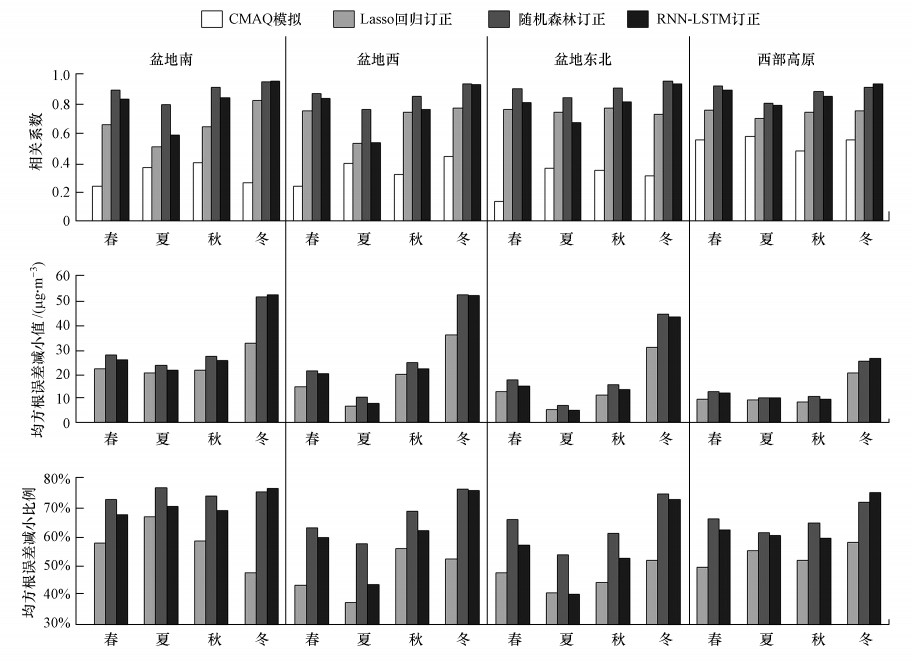 |
| 图 10 成渝地区各区域四季PM2.5浓度模式预报与订正的相关系数、均方根误差减小及均方根误差减小比例 Fig. 10 The seasonal variations of the correlation coefficient between the observed and predicted PM2.5 concentrations for the numerical forecasting and three adjusting methods and the absolute and relative reduction of the root mean squared error between the observed and predicted PM2.5 concentrations caused by three adjusting methods |
从均方根误差减小的数值可以看出, 冬季远高于其他3个季节, 夏季最低.这是由于四川盆地各区域颗粒物污染在冬季最为严重, PM2.5浓度高于其他3个季节, 而夏季颗粒物污染较小, 主要表现为臭氧污染(Zhao et al., 2018).另外, 四川盆地地区冬季颗粒物污染过程持续时间显著高于其他地区, 且污染过程受到静稳天气和低值系统等气象系统的高度影响(宁贵财, 2018;欧阳正午等, 2019), 导致污染物浓度与前日的污染物浓度和高低空气象要素的相关性更强.从图 10中分析结果可以看到, 不同区域的冬季, Lasso回归订正结果的相关系数达到0.75以上, 均方根误差减小48%以上, 随机森林回归和RNN-LSTM订正结果的相关系数达到0.9以上, 均方根误差减小73%以上, 因此, 冬季的订正效果相比其他3个季节更显著.
5 结论(Conclusions)本文基于机器学习方法(Lasso回归、随机森林回归、深度学习RNN-LSTM)对2018年成渝地区空气质量数值模式WRF-CMAQ模拟预报的PM2.5小时浓度进行订正研究.同时, 对成渝地区进行区域划分, 使用空气质量观测数据、气象要素观测数据、WRF模式输出的高低空气象要素构建基础特征变量数据集, 通过随机抽取构建训练数据集和测试数据集, 调整训练参数, 使用训练数据集进行模型训练, 并通过测试数据集检验构建模型的订正效果.其中, Lasso回归算法不仅提高了PM2.5浓度预报的准确性, 还实现了对特征变量的选择, 针对成渝地区4个区域分别进行变量的优选, 降低自变量的维度, 降低机器学习训练和验证的难度, 优化模型.结果表明, 成渝地区4个区域对PM2.5小时浓度预测有主要影响的特征变量组合各不相同.
站点统计检验表明, 基于3种机器学习方法订正后的PM2.5小时浓度相比CMAQ模式模拟预报结果, 偏差显著降低, 相关系数显著提高, 其中, 随机森林回归和RNN-LSTM的订正效果优于Lasso回归.区域统计与站点统计结果较为一致, 其中, Lasso回归订正后的均方根误差减小比例在50%左右, 相关系数在70%以上, 随机森林和RNN-LSTM订正后的均方根误差减小比例在70%左右, 相关系数达90%左右.订正偏差的概率分布表明, 随机森林回归与RNN-LSTM订正后的偏差范围相比Lasso回归集中范围更窄, 最大概率分布更集中.分季节评估结果表明, 整体上3种方法对各季节的订正效果与全年一致, 对于污染较为严重的冬季的订正效果相比其他季节更为显著.随机森林回归和RNN-LSTM的订正效果优于Lasso回归, 随机森林回归和深度学习RNN-LSTM的订正效果相当;22个站点中, 5个站点深度学习RNN-LSTM的订正效果略优于随机森林回归, 17个站点随机森林回归的订正效果略优于深度学习RNN-LSTM;4个区域中, 盆地西和盆地东北随机森林回归的订正效果略优于深度学习RNN-LSTM, 不同季节中, 冬季深度学习RNN-LSTM和随机森林回归的订正效果相当, 其他季节随机森林回归的订正效果较优.
白盛楠, 申晓留. 2019. 基于LSTM循环神经网络的PM2.5预测[J]. 计算机应用与软件, 36(1): 73-76. |
Binkowski F S, Roselle S J. 2003. Models-3 community multiscale air quality (CMAQ) model aerosol component 1.model description[J]. Journal of Geophysical Research Atmospheres, 108(D6): 335-346. |
Cai H K, Gui K, Chen Q L. 2018. Changes in Haze Trends in the Sichuan-Chongqing Region, China, 1980 to 2016[J]. Atmosphere, 9(7): 277. DOI:10.3390/atmos9070277 |
Chen P L Wang T, Matthew K, et al. 2018. Source apportionment of PM2.5 during haze and non-haze episodes in Wuxi, China[J]. Atmosphere, 9(7): 267. DOI:10.3390/atmos9070267 |
程兴宏, 刁志刚, 胡江凯, 等. 2016. 基于CMAQ模式和自适应偏最小二乘回归法的中国地区PM2.5浓度动力-统计预报方法研究[J]. 环境科学学报, 36(8): 2771-2782. |
Guenther A, Karl T, Harley P, et al. 2006. Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature)[J]. Atmospheric Chemistry and Physics, 6(11): 3181-3210. DOI:10.5194/acp-6-3181-2006 |
黄丛吾, 陈报章, 马超群, 等. 2018. 基于极端随机树方法的WRF-CMAQ-MOS模型研究[J]. 气象学报, 76(5): 119-129. |
Halevy A, Norvig P, Pereira F. 2009. The unreasonable effectiveness of data[J]. IEEE Intelligent Systems, 24(2): 8-12. |
李冰, 张妍, 刘石. 2018. 基于LSTM的短期风速预测研究[J]. 计算机仿真, 35(11): 468-473. |
Li M, Wang T, Xie M, et al. 2019. Formation and evolution mechanisms for two extreme haze episodes in the Yangtze River Delta region of China during winter 2016[J]. Journal of Geophysical Research Atmospheres, 124(6): 3607-3623. DOI:10.1029/2019JD030535 |
Li S, Wang T, Solmon F, et al. 2016. Impact of aerosols on regional climate in southern and northern China during strong/weak East Asian summer monsoon years[J]. Journal of Geophysical Research Atmospheres, 121(8): 4069-4081. DOI:10.1002/2015JD023892 |
李颖若, 汪君霞, 韩婷婷, 等. 2019. 回归方法评估气象条件和控制措施对APEC期间北京空气质量的影响[J]. 环境科学, 40(3): 16-26. |
吕梦瑶, 程兴宏, 张恒德, 等. 2018. 自适应偏最小二乘回归法的CUACE模式污染物预报偏差订正改进方法研究[J]. 环境科学学报, 38(7): 2735-2745. |
李文娟, 赵放, 郦敏杰, 等. 2018. 基于数值预报和随机森林算法的强对流天气分类预报技术[J]. 气象, 44(12): 49-58. |
麦健华, 于玲玲, 邓涛, 等. 2018. 基于GRAPES-CMAQ的中山市空气质量预报系统预报效果评估[J]. 热带气象学报, 34(1): 78-86. |
门晓磊, 焦瑞莉, 王鼎, 等. 2019. 基于机器学习的华北气温多模式集合预报的订正方法[J]. 气候与环境研究, 24(1): 118-126. |
宁贵财.2018.四川盆地西北部城市群冬季大气污染气象成因及其数值模拟研究[D].兰州: 兰州大学
|
欧阳正午, 廖婷婷, 陈科艺, 等. 2019. 2014-2017年四川盆地与京津冀地区冬季空气停滞特征及大气质量改善评估对比分析[J]. 环境科学学报, 39(7): 2353-2361. |
Skamarock W C, Klemp J B, Dudhia J, et al.2008.A description of the advanced research WRF version 3[OL].Boulder, Colorado, USA: National Center for Atmospheric Research. 2008-06-01.http://www2.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf
|
孙全德, 焦瑞莉, 夏江江, 等. 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 132-142. |
汤静, 王春林, 谭浩波, 等. 2019. 利用PCA-kNN方法改进广州市空气质量模式PM2.5预报[J]. .热带气象学报, 35(1): 127-136. |
唐孝炎, 张远航, 邵敏. 2006. 大气环境化学[M]. 第2版. 北京: 高等教育出版社.
|
陶晔, 杜景林. 2019. 基于随机森林的长短期记忆网络气温预测[J]. 计算机工程与设计, 40(3): 144-150. |
Tian M, Wang H B, Chen Y, et al. 2017. Highly time-resolved characterization of water-soluble inorganic ions in PM2.5, in a humid and acidic mega city in Sichuan Basin, China[J]. Science of the Total Environment, 580: 224-234. DOI:10.1016/j.scitotenv.2016.12.048 |
Tibshirani R. 2011. Regression shrinkage and selection via the lasso:A retrospective[J]. Journal of the Royal Statistical Society:Series B (Statistical Methodology), 73(3): 273-282. DOI:10.1111/j.1467-9868.2011.00771.x |
Wang H, Tian M, Chen Y, et al. 2018. Seasonal characteristics, formation mechanisms and source origins of PM2.5 in two megacities in Sichuan Basin, China[J]. Atmospheric Chemistry and Physics, 18(2): 865-881. DOI:10.5194/acp-18-865-2018 |
王茜, 吴剑斌, 林燕芬. 2015. CMAQ模式及其修正技术在上海市PM2.5预报中的应用检验[J]. .环境科学学报, 35(6): 1651-1656. |
吴钲, 谢旻, 高阳华, 等. 2018. 利用集合均方根卡尔曼滤波反演重庆地区SO2源排放[J]. 环境科学研究, 31(1): 25-33. |
Xie M, Liao J, Wang T, et al. 2016a. Modeling of the anthropogenic heat flux and its effect on regional meteorology and air quality over the Yangtze River Delta region, China[J]. Atmospheric Chemistry and Physics, 16(10): 6071-6089. DOI:10.5194/acp-16-6071-2016 |
Xie M, Zhu K, Wang T, et al. 2016b. Changes in regional meteorology induced by anthropogenic heat and their impacts on air quality in South China[J]. Atmospheric Chemistry and Physics, 16(23): 15011-15031. DOI:10.5194/acp-16-15011-2016 |
Xie M, Shu L, Wang T J, et al. 2017. Natural emissions under future climate condition and their effects on surface ozone in the Yangtze River Delta region, China[J]. Atmospheric Environment, 152: 162-180. |
杨关盈, 邓学良, 王磊, 等. 2017. 基于CUACE模式产品的订正方法比较研究[J]. 气象科学, 37(6): 839-844. |
Zhan C C, Xie M, Fang D X, et al. 2019. Synoptic weather patterns and their impacts on regional particle pollution in the city cluster of the Sichuan Basin, China[J]. Atmospheric environment, 208: 34-47. DOI:10.1016/j.atmosenv.2019.03.033 |
张岳军, 张怀德, 朱凌云, 等. 2018. 太原市PM2.5预报统计修正模型及其应用检验[J]. 环境科学研究, 31(7): 1207-1213. |
赵俊日, 肖昕, 吴涛, 等. 2018. 空气质量数值预报优化方法研究[J]. 中国环境科学, 38(6): 2047-2054. |
Zhao S P, Yu Y, Yin D Y, et al. 2018. Spatial patterns and temporal variations of six criteria air pollutants during 2015 to 2017 in the city clusters of Sichuan Basin, China[J]. Science of the Total Environment, 624: 540-557. DOI:10.1016/j.scitotenv.2017.12.172 |
Zhong J T, Zhang X, Dong Y, et al. 2018. Feedback effects of boundary-layer meteorological factors on cumulative explosive growth of PM2.5 during winter heavy pollution episodes in Beijing from 2013 to 2016[J]. Atmospheric Chemistry and Physics, 18: 247-258. DOI:10.5194/acp-18-247-2018 |
 2020, Vol. 40
2020, Vol. 40


