同型规范变换的不同预测模型具有的兼容性和等效性

引用本文

李祚泳, 魏小梅, 汪嘉杨. 2020. 同型规范变换的不同预测模型具有的兼容性和等效性[J]. 环境科学学报, 40(4): 1517-1534.

Li Z Y, Wei X M, Wang J Y. 2020. Compatibility and equivalence of different prediction models with same-type normal transform[J]. Acta Scientiae Circumstantiae, 40(4): 1517-1534.

同型规范变换的不同预测模型具有的兼容性和等效性

[PDF全文]

李祚泳, 魏小梅, 汪嘉杨

成都信息工程大学, 资源环境学院, 成都 610225

收稿日期: 2019-07-25; 修回日期: 2019-10-11; 录用日期: 2019-10-11

基金项目: 国家自然科学基金（No.51679155）；四川省科技厅项目（No.19JDJQ0006）；四川省社科规划项目（No.SC18B027）

作者简介: 李祚泳(1944-), 男, 教授, E-mail:lizuoyong@cuit.edu.cn

摘要：传统的不同预测变量的预测模型之间不具有兼容性和等效性，而同型规范变换和误差修正相结合的不同变量的预测模型的预测相对误差与预测对象的维数、样本数及预测模型类型皆无关，仅与预测变量的数据特性、相似样本的模型输出值及其相对误差和相似度有关，因而同型规范变换的不同预测变量的预测模型之间具有兼容性和等效性.其重要意义在于：只要对任意一个预测变量建立了基于规范变换的某种预测模型，就可以将此预测模型直接用于具有同型规范变换的其他预测变量的预测；若再将其与误差修正法相结合，还可以极大地提高模型的预测精度，获得与实际值很接近的预测结果.依据受3个因子影响的灞河口COD_Mn指数数据、受4个因子影响的伊犁河雅马渡站年径流量数据和牡丹江市TSP年均值的时序数据，分别建立具有同型规范变换（n_j=2）的3个不同预测变量的3种智能预测模型和一元线性回归预测模型，并验证了3个不同预测变量的预测模型之间的兼容性和等效性.对同一个预测样本，用同型规范变换和误差修正相结合的不同预测变量的预测模型的实际预测值及其预测相对误差绝对值不仅差异甚微，而且预测值与实际值非常接近，其预测的相对误差绝对值平均值几乎全都小于3%，最大相对误差绝对值均小于5%，小于或远小于20种传统预测模型和方法预测的相应误差.

关键词：规范变换预测模型误差修正兼容性等效性对易性

Compatibility and equivalence of different prediction models with same-type normal transform

LI Zuoyong, WEI Xiaomei, WANG Jiayang

College of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225

Received 25 July 2019; received in revised from 11 October 2019; accepted 11 October 2019

Abstract: Traditional prediction models with different prediction variables are not compatible and equivalent,while the relative prediction errors of different prediction models with different variables combined with the same type of gauge transformation and error correction are not related to the dimension,sample size and type of prediction model,which is only related to the data characteristics of the predicted variables,the output value of the model of similar samples and their relative errors and similarities. Therefore,the predicted models of different predicted variables with the same type of canonical transformation have compatibility and equivalence. Its significance lies in that as long as a prediction model based on canonical transformation is established for any prediction variable,it can be directly applied to the prediction of other prediction variables with the same canonical transformation. If it is combined with the error correction method,the prediction accuracy of the model can be greatly improved,and the prediction results are very close to the actual values. Based on COD_Mn annual mean data affected by three factors in Bahe estuary,annual runoff data affected by four factors in Yamadu Station of Yili River and time series data of TSP annual mean value in Mudanjiang City,three intelligent prediction models and one-variable linear regression prediction models with three different prediction variables with the same type of normative transformation (n_j=2)were established respectively. The compatibility and equivalence of three prediction models with different prediction variables were verified. For the same forecasting sample,the actual forecasting value and the absolute value of the relative error of the forecasting model with different forecasting variables combined with the same type gauge transformation and error correction are not only slightly different,but also very close to the actual value. The average absolute value of relative error is almost all less than 3%,and the maximum absolute value of relative error is less than 5%,which is less than or far less than the corresponding error of 20 traditional prediction models and methods.

Keywords: canonical transformation prediction model error correction compatibility equivalence commutativity

1 引言(Introduction)

由于长期以来人类对地球自然资源的过度开发, 导致全球的生态平衡已受到破坏, 环境污染日趋严重.因此, 我们必须保护好地球的生态环境, 走一条人类可持续的绿色发展之路.走可持续的绿色发展之路就是不仅要重视环境的现在, 更要关注环境的未来.为此, 人们提出了数十种环境预测的模型与方法.其中, 最常见的是各种非机理性的统计预测模型(Fu, 2011；Thoe et al., 2012；Tan et al., 2012；Chen et al., 2013；Comrie, 2013；王保良等, 2016)和智能预测模型(Xi et al., 2012；笪英云等, 2015；Liu et al., 2015；Moazami et al., 2016；Shaban et al., 2016；张旭东等, 2016；孙宝磊等, 2017).不过, 传统的非机理性预测的模型与方法存在以下不足：①对高维、非线性复杂问题, 传统预测模型和方法都存在模型结构复杂和“维数灾难”及样本数困难；②用于环境预测往往预测精度不高, 结果不理想；③传统的预测模型和方法的共同局限是不能规范和普适.为此, 笔者提出对因子进行规范变换, 以简化模型结构, 克服了“维数灾难”和样本数困难；还提出预测样本模型输出的误差修正法, 极大地提高了模型的预测精度(李祚泳等, 2018；2019a；2019b)；并论证了精度的提高与预测变量的影响因子数目、样本数目、样本原始数据分布特性和变化规律及选用何种预测模型均无关, 因而此种预测模型不仅具有普遍意义, 而且变得普适、规范、简单、实用.

不仅如此, 研究还表明, 只要变换式中的幂指数n_j是同为2、1或0.5的同型规范变换的不同预测变量的预测模型, 则彼此之间皆具有“兼容性”、“等效性”和“对称性”, 从而使预测问题变得极大的简化、方便和省时.

2 同型规范变换的不同预测模型的兼容性和等效性的理论基础(Theoretical basis of compatibility and equivalence of different prediction models with same-type normal transform)

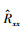
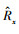
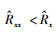
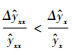
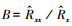
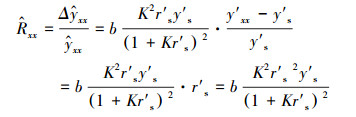
由文献(李祚泳等, 2019a)4.3节预测模型误差的理论分析可导出以下结论：若用误差修正公式修正后的预测样本模型输出值计算得到的样本实际预测值的相对误差绝对值为 (式(1)), 未用误差修正公式修正的模型输出值计算得到的样本实际预测值的相对误差绝对值为, 则一定有, 即；且两种相对误差绝对值的比值 (式(2)).为叙述简便, 以下相对误差绝对值简称相对误差.

(1)

(2)

式中, K、y′_s和r′_s分别为与预测样本模型输出值相近的拟合相似样本的相似度、相似样本的模型输出值及其拟合相对误差；参数b=10/n_j, 其中, n_j为预测变量变换式中的幂指数, 取值为n_j=0.5、1、2, 它决定预测变量的变换式的类型, 与预测变量原始数据的分布特性及其变化规律有关.

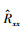
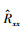
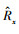
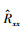
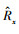
由式(1)可知, 相对误差与相似样本的K、y′_s和r′_s有关, 与预测变量有关的仅有表征原始数据的分布特性及其变化规律的b, 而与预测变量的建模样本数n、影响因子数m无关, 也与所选择的何种预测模型无关.由式(2)可知, 两种相对误差的比值B =/ 仅由相似样本的相似度K和拟合相对误差r′_s决定, 且一定满足B < 1或B < < 1.因此, 若将基于规范变换的某个预测变量的某种预测模型直接用于具有同型规范变换的其他不同预测变量的预测, 由于变换式中幂指数n_j相同, 因而b也相同, 故只要具有同型规范变换的其他预测样本模型输出的相似样本选择适当, 则由式(2)计算得到的两种相对误差的比值B=/也一定小于或远小于1.可见, 基于同型规范变换的预测变量与误差修正结合的预测模型彼此之间具有“兼(相)容性”和“等效性”.所谓“兼容性”是指任意一个基于规范变换的预测变量的某种预测模型, 都可以直接用于具有同型规范变换的其他预测变量的预测, 反之亦然, 因而满足同型规范变换的不同预测变量的预测模型是彼此协调和兼容的.所谓“等效性”是指对同一个预测变量, 用具有同型规范变换的不同预测变量的预测模型进行预测, 其效果(实际预测值及其相对误差)是相同的, 即彼此等效.具有上述两个特性的规范变换满足“对称性”.所谓“对称性”是指与误差修正法相结合的同型规范变换的不同预测变量的预测模型, 彼此互换(对易)使用, 其预测效果差异甚微, 具有近似稳定“不变性”.正是由于同型规范变换的不同预测变量的预测模型之间具有的兼容性和等效性, 并结合误差修正法, 才保证了不同预测模型的预测效果的稳定性, 从而使对基于规范变换的某个预测变量建立的某种预测模型, 可以直接用于具有同型规范变换的其他预测变量的预测, 而无需对其再建模.因而兼容性和等效性在预测模型中起着重要作用, 具有重要意义.图 1形象、直观地描述了分别位于三角形三顶点的预测变量的同型规范变换与预测模型的兼容性、等效性和预测模型预测效果的稳定性三者之间的逻辑关系.

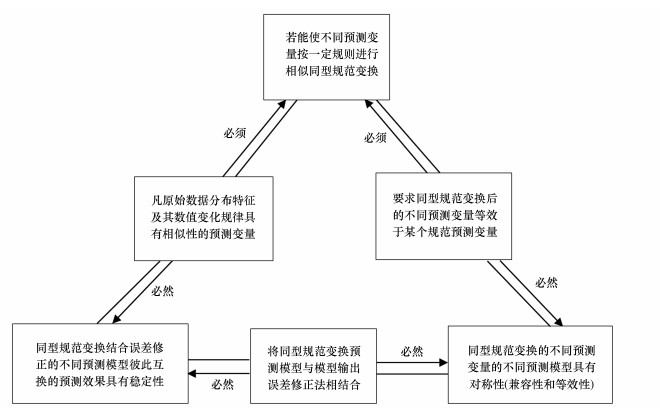图 1 预测变量的同型规范变换、预测模型的对称性和预测效果的稳定性三者之间的逻辑关系 Fig. 1 The logical relationship among the homo-canonical transformation of predictive variables, the symmetry of predictive models and the stability of predictive effects

以具有同型规范变换(n_j=2)的灞河口水质COD_Mn的年均值、伊犁河雅马渡站的年径流量及牡丹江市空气总悬浮颗粒物(TSP)年均值的时序数据3个不同预测变量为例, 分别建立基于同型规范变换的3种智能预测模型和一元线性回归预测模型, 并验证不同预测变量的预测模型之间的兼容性、等效性和对称性.

3 基于同型规范变换的不同预测变量的预测模型(Prediction model of different predictive variables based on homogeneous normal transform) 3.1 基于规范变换的灞河口COD_Mn指数的3种智能预测模型和一元线性回归预测模型 3.1.1 COD_Mn指数年均值及其影响因子的参照值和规范变换式的设置

西安市灞河口11年(1993—2003年)COD_M_n(C_y)的年均值(c_y)及其3个影响因子C_j(j=1、2、3)的监测数据c_j(j=1、2、3)参见文献(房平等, 2011).设置如式(3)和式(4)组成的规范变换式, 由式(3)和式(4)计算得到各影响因子的规范值x_i′及预测变量的规范值y_i′.

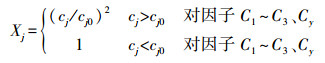
(3)

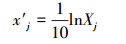
(4)

式中, c_j和c_j₀分别为因子或预测变量实际值和设置的参照值, 3个因子和预测变量的参照值c_j₀分别设置为0.7、0.5、0.8和0.8；c_j、c_j₀和c_y的单位皆为mg·L^-1；X_j和x_j′分别为因子或预测变量的变换值和规范值.

3.1.2 基于COD_Mn规范值的3种智能预测模型和一元线性回归预测模型

依据基于规范变换的NV-FNN、NV-PPR、NV-SVR 3种智能预测模型(李祚泳等, 2019a;2018)和一元线性回归预测模型(NV-ULR)(李祚泳等, 2019b)的建模理论和方法, 分别得到COD_Mn指数的NV-FNN、NV-PPR、NV-SVR和NV-ULR预测模型, 具体如式(5)~式(11)所示.

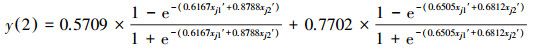
(5)

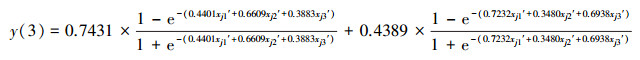
(6)

(7)

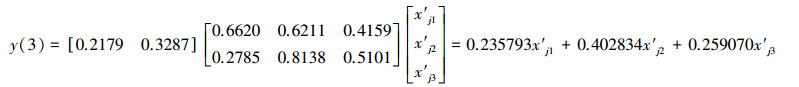
(8)

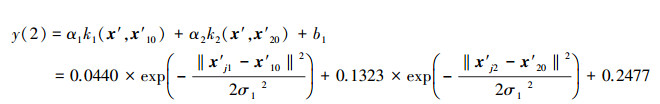
(9)

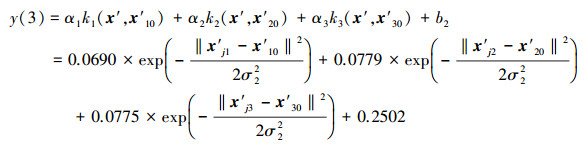
(10)

式中, k₁、k₂、k₃皆为径向基核函数；x′₁₀、x′₂₀和x′₃₀分别是3个核函数的恒定中心矢量；||·||为用均方根距离表示的两个样本之间的范数；σ为径向基核函数的宽度参数, 分别为σ₁=0.0945和σ₂=0.1068；b₁、b₂为阈值；α_i(i=1, 2, 3)为支持向量对应的系数.

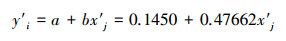
(11)

式(5)~式(11)中, x′_j₁、x′_j₂、x′_j₃分别为将每个样本的m(j= 1, 2, …, m)个因子规范值按顺序排列, 并首、尾两个因子相连构成循环, 其中, 从第j个因子开始, 依顺序取的连续3个因子规范值.

3.2 基于伊犁河雅马渡站年径流量规范值的智能预测模型和一元线性回归预测模型 3.2.1 年径流量及其影响因子的参照值和规范变换式的设置

新疆伊犁河雅马渡站23年(1953—1975年)的年径流量(C_y)及其4个影响因子(C_j, j=1~4)的监测数据c_j参见文献(崔东文, 2013).设置如式(12)的变换式, 由式(12)和式(4)计算得到各影响因子的规范值x_i′及径流量的规范值y_i′.

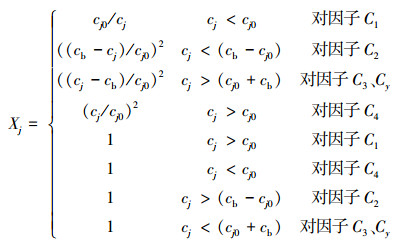
(12)

式中, C₁~C₄和C_y的参照值c_j₀分别设置为3.5、0.1、0.19、28和30；C₂、C₃和C_y的阈值c_b分别为1.5、0.07和100.c_j₀的单位与相应c_j的单位相同.

3.2.2 年径流量规范值的3种智能预测模型和一元线性回归预测模型

与3.1.2节COD_Mn 3种智能预测模型和一元线性回归预测模型的建模过程类似, 分别得到径流量的NV-FNN、NV-PPR、NV-SVR和NV-ULR预测模型, 具体如式(13)~式(19)所示.其中, 式(17)和式(18)中的σ分别为σ₁=0.1120和σ₂=0.1639.

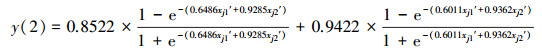
(13)

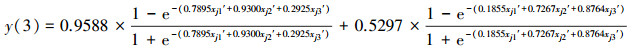
(14)

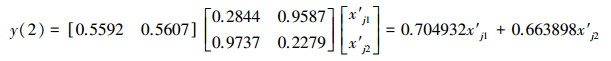
(15)

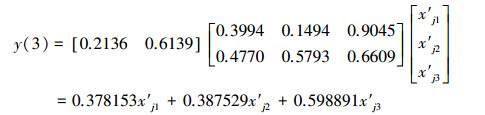
(16)

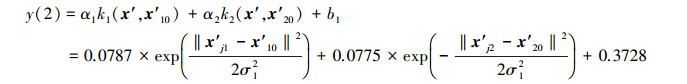
(17)

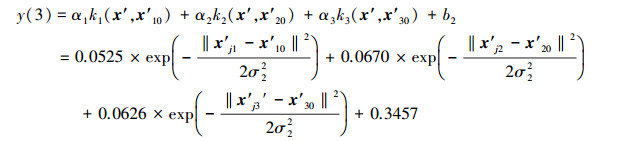
(18)

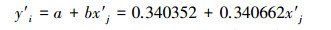
(19)

3.3 基于牡丹江TSP年均值时序数据规范值的智能预测模型和一元线性回归预测模型 3.3.1 TSP年均值的参照值和规范变换式的设置

牡丹江市1991—2002年总悬浮颗粒物(TSP)年均值的时间序列数据见文献(陈世权等, 2003).设置如式(20)所示的TSP时序数据变换式, 由式(20)和式(4)计算得到TSP的规范值y_i′.

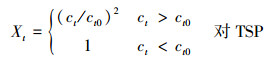
(20)

式中, 参照值c_t0=0.05.c_t和c_t0的单位相同, 为mg·m^-3.

3.3.2 TSP规范值的3类智能预测模型和一元线性回归预测模型

与3.1.2节COD_Mn 3类智能预测模型和一元线性回归预测模型的建模过程类似, 分别得到TSP的NV-FNN、NV-PPR、NV-SVR和NV-ULR预测模型, 具体如式(21)~式(27)所示.其中, 式(25)和式(26)中的σ分别为σ₁=0.1503和σ₂=0.1869

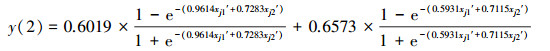
(21)

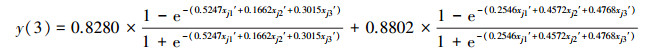
(22)

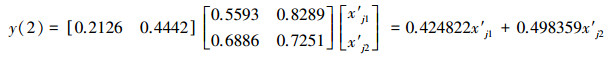
(23)

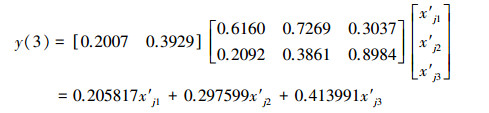
(24)

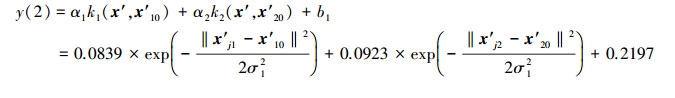
(25)

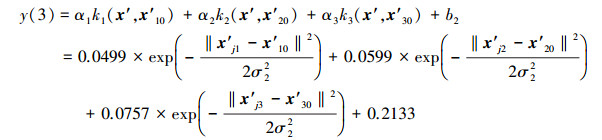
(26)

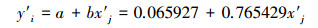
(27)

4 同型规范变换的不同预测模型的兼容性和等效性的验证实例(Examples of compatibility and equivalence of different prediction models with same-type normal transform) 4.1 同型规范变换的不同预测变量的预测模型用于灞河口COD_Mn指数预测 4.1.1 基于同型规范变换的雅马渡站径流预测模型的灞河口COD_Mn指数预测

① COD_Mn指数年均值及其影响因子的参照值和规范变换式的设置仍设置灞河口COD_Mn(C_y)的年均值(c_y)及其3个影响因子C_j的监测数据c_j(j=1, 2, 3)的变换式，如式(3)所示, 只是COD_Mn的参照值设置为c_y₀=0.5.由式(3)和式(4)计算得到COD_Mn的规范值y_i0′, 结果见表 1.

表 1 4种预测模型的建模样本拟合输出值y′_i及预测样本计算输出值y′_x Table 1 Fitting output value y′_i of modeling sample and calculating output value y′_x of predicting sample based on 4 prediction models

年份/序号	基于径流预测模型的COD_Mn建模样本拟合输出及预测样本计算输出							预测量的规范值y_i0′
年份/序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	预测量的规范值y_i0′
1993/1	0.3638	0.3728	0.3618	0.3607	0.4100	0.4398	0.4304	0.3358
1994/2	0.4735	0.4828	0.4758	0.4743	0.4796	0.4804	0.4588	0.4040
1995/3	0.3749	0.3843	0.3738	0.3727	0.4381	0.4205	0.4334	0.3409
1996/4	0.5881	0.5952	0.5987	0.5969	0.5349	0.5227	0.4894	0.5058
1997/5	0.5140	0.5227	0.5185	0.5169	0.5143	0.5068	0.4694	0.4381
1998/6	0.4471	0.4566	0.4484	0.4470	0.4583	0.4584	0.4519	0.3869
1999/7	0.5370	0.5454	0.5433	0.5416	0.5137	0.5092	0.4756	0.4585
2000/8	0.3754	0.3846	0.3691	0.3680	0.4426	0.4385	0.4322	0.3274
2001/9	0.4654	0.4746	0.4670	0.4656	0.4853	0.4835	0.4566	0.4003
2002/10^*	0.4779	0.4870	0.4802	0.4787	0.4897	0.4888	0.4599	0.4139
2003/11^*	0.4991	0.5080	0.5026	0.5011	0.4979	0.4966	0.4654	0.4213

年份/序号	基于TSP时序预测模型的COD_Mn建模样本拟合输出及预测样本计算输出							预测量的规范值y_i0′
年份/序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	预测量的规范值y_i0′
1996/4	0.2974	0.2992	0.2989	0.2971	0.3281	0.3484	0.3138	0.4693
1997/5	0.3467	0.3502	0.3512	0.3490	0.3544	0.3684	0.3571	0.4016
1998/6	0.3565	0.3603	0.3617	0.3594	0.3604	0.3727	0.3658	0.3504
1999/7	0.3697	0.3739	0.3758	0.3735	0.3735	0.3829	0.3775	0.4233
2000/8	0.3566	0.3603	0.3617	0.3594	0.3710	0.3812	0.3658	0.2909
2001/9	0.3246	0.3272	0.3276	0.3256	0.3444	0.3608	0.3376	0.3638
2002/10^*	0.3285	0.3312	0.3317	0.3297	0.3473	0.3629	0.3410	0.3774
2003/11^*	0.3152	0.3175	0.3176	0.3156	0.3411	0.3585	0.3293	0.3848
注：“*”表示预留的预测检验样本.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值及预测样本的计算输出值将由式(3)和式(4)计算得到的COD_Mn的各因子的规范值x_i′代入3.2.2节雅马渡站的年径流量预测模型公式(13)~(19), 计算得到两种结构的3种智能预测模型和NV-ULR预测模型前9年建模样本(1993—2001年)的模型拟合输出值及后2年检测(预测)样本(标记为2002^*、2003^*)的模型计算输出值, 如表 1所示.计算得到3种智能预测模型和NV-ULR预测模型的前9年建模样本的模型输出的拟合相对误差绝对值, 如表 2所示.

表 2 基于4种预测模型的建模样本的拟合相对误差r′_i Table 2 Fitting relative errors of modeling samples based on four prediction models

年份/序号	基于径流预测模型的COD_Mn拟合样本模型输出相对误差r′_i
年份/序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR
1993/1	8.34%	11.02%	7.74%	7.42%	22.10%	30.97%	28.17%
1994/2	17.20%	19.50%	17.77%	17.40%	18.71%	18.84%	13.56%
1995/3	9.97%	12.73%	9.65%	9.33%	28.51%	23.35%	27.13%
1996/4	16.27%	17.67%	18.37%	18.01%	5.75%	3.34%	3.24%
1997/5	17.32%	19.31%	18.35%	17.99%	17.39%	15.68%	7.14%
1998/6	15.56%	18.01%	15.90%	15.53%	18.45%	18.48%	16.80%
1999/7	17.12%	18.89%	18.50%	18.12%	12.04%	11.06%	3.73%
2000/8	14.66%	17.47%	12.74%	12.40%	35.19%	33.93%	32.00%
2001/9	16.26%	18.56%	16.66%	16.31%	21.23%	20.78%	14.06%

年份/序号	基于TSP时序预测模型的COD_Mn拟合样本模型输出相对误差r′_i
年份/序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR
1996/4	36.63%	36.25%	36.30%	36.69%	30.09%	25.76%	33.13%
1997/5	13.67%	12.80%	12.55%	13.10%	11.75%	8.27%	11.08%
1998/6	1.74%	2.83%	3.22%	2.57%	2.85%	6.36%	4.39%
1999/7	12.66%	11.67%	11.22%	11.76%	11.76%	9.54%	10.82%
2000/8	22.59%	23.86%	24.34%	23.55%	27.55%	31.04%	25.75%
2001/9	10.78%	10.06%	9.95%	10.67%	5.33%	0.82%	7.20%

③ 预测样本模型输出的误差修正及修正后的COD_Mn指数的实际预测值从表 1可见, 分别与雅马渡站径流预测模型的2002^*年、2003^*年COD_Mn预测样本的4种预测模型输出相似的拟合样本如表 3所示.用误差修正公式(李祚泳等, 2019a)修正后的2个检测(预测)样本的4种预测模型的输出值Y_x′, 如表 4所示.再由式(3)和式(4)的逆运算, 计算得到4种预测模型对2002^*年、2003^*年COD_Mn指数的实际预测值c_yx, 如表 5所示.表 4和表 5中还分别列出2002^*年、2003^*年COD_Mn指数实际值的规范值Y_x₀′和实际值c_y₀.

表 3 基于4种预测模型的预测样本输出的相似样本 Table 3 Similar samples of prediction samples output based on four prediction models

表 4 基于4种预测模型的预测样本误差修正后的模型输出值 Table 4 Model output values based on the corrected sample error of four prediction models

表 5 基于4种预测模型的预测样本误差修正后的实际预测值 Table 5 Actual predicted values based on the corrected sample error of four prediction models

④ 多种预测模型的实际预测值的相对误差及比较2个检测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)如表 6所示.

表 6 预测样本的多种预测模型的预测相对误差的绝对值及其平均值和最大值r_x Table 6 Absolute values of relative errors, their mean values and maximum values of various prediction models for prediction samples

预测样本	基于雅马渡站径流预测模型的COD_Mn预测样本的相对误差r_x								基于牡丹江TSP时序预测模型的COD_Mn预测样本的相对误差r_x								基于多因子灞河口COD_Mn预测模型的预测样本的相对误差r_x
预测样本	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	LS-SVM	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	BP网络	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	RBF网络
2002^*	2.78%	2.78%	1.77%	1.77%	3.28%	0.25%	1.26%	4.55%	0	0.25%	1.01%	0.51%	1.26%	0	1.52%	9.85%	0.25%	1.01%	1.52%	1.01%	0	0.76%	0.25%	7.58%
2003^*	1.70%	1.70%	1.70%	1.95%	0.00%	0.73%	0.24%	5.36%	0.97%	0.49%	0.24%	0.73%	0.24%	1.95%	0.24%	11.44%	0.49%	0.49%	0.00%	0.00%	0.49%	0.73%	0.73%	9.73%
平均值	2.24%	2.24%	1.74%	1.86%	1.64%	0.49%	0.75%	4.96%	0.49%	0.37%	0.62%	0.62%	0.75%	0.98%	0.88%	10.65%	0.37%	0.75%	0.76%	0.51%	0.25%	0.75%	0.49%	8.67%
最大值	2.78%	2.78%	1.77%	1.95%	3.28%	0.73%	1.26%	5.36%	0.97%	0.49%	1.01%	0.73%	1.26%	1.95%	1.52%	11.44%	0.49%	1.01%	1.52%	1.01%	0.49%	0.76%	0.73%	9.73%

4.1.2 基于同型规范变换的牡丹江市TSP时序预测模型的灞河口COD_Mn指数的时序预测

由于牡丹江市TSP时间序列的4种预测模型只是时间序列的预测模型, 因此, 也只用于建立灞河口COD_Mn指数的时间序列(k=3)预测模型.

① COD_Mn指数年均值时序变量的参照值和规范变换式的设置设置灞河口COD_Mn(C_y)的年均值(c_y)时序的监测数据c_j(j=1, 2, 3)的变换式仍如式(3)所示, 只是COD_Mn的参照值设置为c_y₀=0.6.由式(3)和式(4)计算得到COD_Mn时序变量的规范值y₀′, 如表 1所示.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值及预测样本的计算输出值将由式(3)和(4)计算得到的COD_Mn的时序规范值x_i′组成的3个因子(k=3)代入3.3.2节牡丹江市TSP预测模型公式(21)~(27)中, 计算得到两种结构的3种智能预测模型和NV-ULR预测模型前6年建模样本(1996—2001年)的模型拟合输出值及后2年检测(预测)样本(2002^*年、2003^*年)的模型计算输出值(表 1).同时, 计算得到3种智能预测模型和NV-ULR预测模型的前6年建模样本的模型输出的拟合相对误差绝对值(表 2).

③ 预测样本模型输出的误差修正及修正后的COD_Mn指数的实际预测值从表 1可见, 分别与基于牡丹江市TSP预测模型的2002^*年、2003^*年COD_Mn预测样本的4种预测模型输出相似的拟合样本见表 3.用误差修正公式修正后的2个检测(预测)样本的4种预测模型的输出值Y_x′见表 4.再由式(3)和式(4)的逆运算, 计算得到4种预测模型对2002^*年、2003^*年COD_Mn指数的实际预测值c_yx见表 5.表 4和表 5中还分别列出2002^*年、2003^*年COD_Mn指数实际值的规范值Y_x₀′和实际值c_y₀.

④ 多种预测模型的实际预测值的相对误差及比较2个预测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)见表 6.表 6中还列出直接用基于多因子灞河口预测模型式(5)~式(11)及传统的LS-SVM、BP和RBF等3种预测模型的预测相对误差r_x.可见, 3种同型规范变换的不同预测模型的预测相对误差平均值和最大值均远小于传统的3种预测模型的相应误差.

4.2 同型规范变换的不同预测变量的预测模型用于雅马渡站径流量预测 4.2.1 基于同型规范变换的灞河口COD_Mn预测模型的雅马渡站径流量预测

① 年均值及其影响因子的参照值和规范变换式的设置雅马渡站径流(C_y)的年均值(c_y)及其4个影响因子C_j(j=1~4)的监测数据c_j见文献(崔东文, 2013).仍设置如式(12)所示的变换式.除径流量的参照值设置为c_y₀=50外, 因子的参照值和阈值均不变.由式(12)和式(4)计算得到各影响因子的规范值x_i′, 预测变量的规范值y_i0′, 如表 7所示.

表 7 4种预测模型的建模样本拟合输出值y′_i及预测样本计算输出值y′_x Table 7 Fitting output value y′_i of modeling sample and calculating output value y′_x of predicting sample based on 4 prediction models

年份序号	基于COD_Mn预测模型的径流建模样本拟合输出及预测样本计算输出							预测量的规范值y_i0′
年份序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	预测量的规范值y_i0′
1	0.2888	0.2877	0.2796	0.2804	0.3153	0.3559	0.2939	0.3187
2	0.2799	0.2791	0.2708	0.2716	0.3200	0.3496	0.2892	0.3649
3	0.2846	0.2836	0.2755	0.2763	0.3219	0.3491	0.2917	0.3481
4	0.3086	0.3073	0.2995	0.3004	0.3469	0.3835	0.3045	0.3869
5	0.2718	0.2710	0.2627	0.2634	0.3122	0.3471	0.2849	0.2773
6	0.3599	0.3575	0.3515	0.3525	0.4005	0.4515	0.3322	0.3909
7	0.3476	0.3456	0.3389	0.3399	0.3972	0.4462	0.3255	0.4134
8	0.3537	0.3515	0.3452	0.3462	0.3995	0.4500	0.3288	0.4046
9	0.3012	0.3000	0.2919	0.2928	0.3452	0.3912	0.3005	0.3146
10	0.2522	0.2516	0.2432	0.2439	0.2948	0.3284	0.2745	0.3017
11	0.2576	0.2568	0.2485	0.2492	0.2932	0.3291	0.2773	0.3328
12	0.2966	0.2956	0.2876	0.2884	0.3365	0.3696	0.2981	0.3926
13	0.2354	0.2350	0.2268	0.2274	0.2839	0.3045	0.2658	0.2773
14	0.2722	0.2714	0.2631	0.2639	0.3096	0.3410	0.2851	0.3792
15	0.2709	0.2700	0.2617	0.2625	0.3105	0.3491	0.2844	0.3104
16	0.2725	0.2716	0.2633	0.2641	0.3085	0.3418	0.2852	0.2659
17	0.3327	0.3311	0.3239	0.3249	0.3736	0.4169	0.3175	0.4072
18	0.3198	0.3182	0.3107	0.3116	0.3472	0.3953	0.3105	0.3597
19	0.2951	0.2940	0.2858	0.2867	0.3385	0.3821	0.2972	0.3474
20^*	0.2633	0.2626	0.2543	0.2550	0.3040	0.3343	0.2804	0.2908
21^*	0.3248	0.3232	0.3157	0.3166	0.3737	0.4220	0.3131	0.3590
22^*	0.2708	0.2700	0.2617	0.2625	0.3108	0.3437	0.2844	0.2562
23^*	0.2650	0.2643	0.2560	0.2567	0.3064	0.3372	0.2813	0.2783
4	0.4034	0.4084	0.4118	0.4092	0.3769	0.3855	0.4074	0.4890
5	0.4217	0.4283	0.4328	0.4301	0.3867	0.3925	0.4248	0.3794
6	0.3971	0.4026	0.4058	0.4033	0.3684	0.3791	0.4024	0.4931
7	0.4090	0.4152	0.4190	0.4163	0.3727	0.3821	0.4133	0.5155
8	0.4163	0.4229	0.4271	0.4245	0.3735	0.3827	0.4200	0.5067
9	0.4514	0.4598	0.4663	0.4634	0.3951	0.3983	0.4525	0.4167
10	0.4305	0.4377	0.4428	0.4400	0.3838	0.3903	0.4330	0.4039
11	0.3995	0.4051	0.4084	0.4059	0.3694	0.3801	0.4046	0.4350
12	0.3795	0.3841	0.3864	0.3840	0.3623	0.3751	0.3863	0.4947
13	0.4013	0.4070	0.4104	0.4078	0.3727	0.3824	0.4062	0.3794
14	0.3945	0.3998	0.4028	0.4003	0.3663	0.3776	0.3999	0.4814
15	0.4074	0.4134	0.4171	0.4145	0.3723	0.3818	0.4118	0.4125
16	0.3844	0.3893	0.3918	0.3894	0.3610	0.3738	0.3908	0.3681
17	0.3812	0.3859	0.3884	0.3859	0.3579	0.3714	0.3879	0.5094
18	0.3890	0.3942	0.3970	0.3945	0.3591	0.3723	0.3951	0.4618
19	0.4028	0.4087	0.4121	0.4096	0.3675	0.3782	0.4076	0.4496
20^*	0.4256	0.4325	0.4372	0.4345	0.3867	0.3925	0.4284	0.3930
21^*	0.3932	0.3984	0.4014	0.3989	0.3695	0.3801	0.3987	0.4612
22^*	0.3930	0.3983	0.4012	0.3987	0.3694	0.3801	0.3986	0.3584
23^*	0.3672	0.3713	0.3731	0.3708	0.3490	0.3647	0.3753	0.3804
注：年份序号1~23代表1953—1957年; “*”表示预留的预测检验样本.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值及预测样本的计算输出值将计算得到的各因子的规范值x_i′代入3.1.2节灞河口COD_Mn预测公式(5)~式(11)中, 计算得到3种智能预测模型和NV-ULR预测模型前19年建模样本的模型拟合输出值及后4年检测样本(序号20^*~23^*)的模型计算输出值, 如表 7所示.同时, 计算得到3种智能预测模型和NV-ULR预测模型的前19年建模样本的模型输出的拟合相对误差绝对值, 如表 8所示.

表 8 4种预测模型的建模样本的拟合相对误差r′_i Table 8 Fitting relative errors of modeling samples based on four prediction models

年份序号	基于COD_Mn预测模型的径流拟合样本模型输出相对误差r′_i
年份序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR
1	9.38%	9.73%	12.27%	12.02%	1.07%	11.67%	8.60%
2	23.29%	23.51%	25.79%	25.57%	12.30%	4.19%	20.75%
3	18.24%	18.53%	20.86%	20.63%	7.53%	2.87%	16.20%
4	20.24%	20.57%	22.59%	22.36%	10.84%	0.88%	22.34%
5	1.98%	2.27%	5.27%	5.01%	12.59%	25.17%	2.74%
6	7.93%	8.54%	10.08%	9.82%	2.46%	15.50%	15.02%
7	15.92%	16.40%	18.02%	17.78%	3.92%	7.93%	21.26%
8	12.58%	13.12%	14.68%	14.43%	1.26%	11.22%	18.73%
9	4.26%	4.46%	7.22%	6.93%	9.73%	24.35%	4.48%
10	16.40%	16.60%	19.39%	19.16%	2.29%	8.85%	9.02%
11	22.60%	22.84%	25.33%	25.12%	11.90%	1.11%	16.68%
12	24.45%	24.70%	26.74%	26.54%	14.29%	5.86%	24.07%
13	15.11%	15.25%	18.21%	17.99%	2.38%	9.81%	4.15%
14	28.22%	28.43%	30.62%	30.41%	18.35%	10.07%	24.82%
15	12.73%	13.02%	15.69%	15.43%	0.03%	12.47%	8.38%
16	2.48%	2.14%	0.98%	0.68%	16.02%	28.55%	7.26%
17	18.30%	18.69%	20.46%	20.21%	8.25%	2.38%	22.03%
18	11.09%	11.54%	13.62%	13.37%	3.48%	9.90%	13.68%
19	15.05%	15.37%	17.73%	17.47%	2.56%	9.99%	14.45%
4	17.50%	16.48%	15.79%	16.32%	22.92%	21.17%	16.69%
5	11.15%	12.89%	14.07%	13.36%	1.92%	3.45%	11.97%
6	19.47%	18.35%	17.70%	18.21%	25.29%	23.12%	18.39%
7	20.66%	19.46%	18.72%	19.24%	27.70%	25.88%	19.83%
8	17.84%	16.54%	15.71%	16.22%	26.29%	24.47%	17.11%
9	8.33%	10.34%	11.90%	11.21%	5.18%	4.42%	8.59%
10	6.59%	8.37%	9.63%	8.94%	4.98%	3.37%	7.20%
11	8.16%	6.87%	6.11%	6.69%	15.08%	12.62%	6.99%
12	23.29%	22.36%	21.89%	22.38%	26.76%	24.18%	21.91%
13	5.77%	7.27%	8.17%	7.49%	1.77%	0.79%	7.06%
14	18.05%	16.95%	16.33%	16.85%	23.91%	16.85%	16.93%
15	1.24%	0.22%	1.12%	0.48%	9.75%	7.44%	0.17%
16	4.43%	5.76%	6.44%	5.79%	6.44%	1.93%	6.17%
17	25.17%	24.24%	23.75%	24.24%	23.75%	29.74%	23.85%
18	15.76%	14.64%	14.03%	14.57%	22.24%	19.38%	14.44%
19	10.41%	9.10%	8.34%	8.90%	18.27%	15.88%	9.34%

③ 预测样本模型输出的误差修正及修正后的径流量的实际预测值从表 7可见, 分别与灞河口COD_Mn预测模型的序号20^*~23^*径流预测样本的4种预测模型输出相似的拟合样本如表 9所示.用误差修正公式修正后的4个检测(预测)样本的4种预测模型的输出值Y_x′如表 10所示.再由式(12)和式(4)的逆运算, 计算得到4种预测模型对序号20^*~23^*径流的实际预测值c_yx, 如表 11所示.表 10和表 11中还分别列出序号20^*~23^*径流的实际值的规范值Y_x₀′和实际值c_y₀.

表 9 4种预测模型的预测样本输出的相似样本 Table 9 Similar samples of prediction samples output based on four prediction models

表 10 4种预测模型的预测样本误差修正后的模型输出值 Table 10 Model output values based on the corrected sample error of four prediction models

表 11 4种预测模型的预测样本误差修正后的模型实际预测值 Table 11 Actual predicted values based on the corrected sample error of four prediction models

④ 多种预测模型的实际预测值的相对误差及比较4个检测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)如表 12所示.

表 12 4个检测样本的多种预测模型的预测相对误差的绝对值及其平均值和最大值r_x Table 12 The absolute value of relative error, its average value and maximum value r_x of multiple prediction models with four test samples

预测样本序号	基于灞河口COD_Mn预测模型的雅马渡站径流预测样本的相对误差r_x							基于牡丹江TSP时序预测模型的雅马渡站径流预测样本的相对误差r_x							基于雅马渡站多因子径流预测模型的预测样本的相对误差r_x							传统预测模型用于雅马渡站径流预测的预测样本的相对误差r_x								传统预测模型用于雅马渡站径流预测的预测样本的相对误差r_x
预测样本序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	近邻估计^[1]	模糊回归^[1]	模糊识别^[2]	RBF^[3](一)	RBF^[4](二)	IEA-BP网络^[4]	传统BP^[4]	GRNN网络^[4]	双隐层BP^[4]	三隐层BP ^[4]	BSA-PPR^[5]	LS-SVM^[6]	PCA-SVM^[7]	FSVM^[8]	SVM^[8]	门限回归TR^[9]
20^*	2.23%	2.23%	0.64%	0.64%	3.82%	3.18%	0.64%	0.64%	0.64%	0.64%	0.64%	0.32%	0.00%	1.27%	0.96%	1.59%	1.27%	1.91%	0.00%	0.64%	1.91%	7.76%	7.32%	3.72%	5.70%	7.79%	1.05%	18.30%	4.35%	2.01%	6.16%	4.83%	1.90%	3.79%	1.21%	8.03%	10.86%
21^*	2.43%	2.68%	2.74%	2.74%	4.98%	0.50%	1.50%	0.25%	1.25%	0.25%	0.25%	0.00%	1.75%	1.00%	2.74%	2.74%	2.99%	2.99%	0.50%	0.87%	0.25%	5.41%	3.74%	4.67%	0.99%	3.40%	7.17%	0.33%	4.62%	0.06%	9.48%	5.10%	16.00%	8.87%	3.21%	6.43%	2.97%
22^*	0.18%	0.36%	0.36%	0.00%	2.14%	3.57%	1.43%	2.14%	0.36%	2.14%	0.71%	0.36%	0.36%	1.43%	1.07%	2.85%	0.71%	0.71%	3.21%	1.79%	3.21%	19.18%	14.64%	14.37%	13.90%	0.82%	0.63%	10.13%	0.02%	6.73%	2.85%	0.82%	9.30%	9.46%	10.78%	24.10%	18.57%
23^*	0.00%	1.00%	1.66%	1.33%	2.33%	1.33%	1.33%	2.33%	2.99%	2.66%	2.33%	1.33%	2.33%	0.33%	1.33%	1.33%	1.66%	1.99%	1.66%	2.33%	1.00%	9.01%	12.29%	7.51%	12.30%	11.38%	10.66%	21.58%	13.77%	6.72%	7.67%	11.56%	5.60%	6.36%	8.57%	15.88%	13.46%
平均值	1.24%	1.57%	1.35%	1.18%	3.32%	2.15%	1.23%	1.34%	1.31%	1.42%	0.98%	0.50%	1.11%	1.01%	1.53%	2.13%	1.66%	1.90%	1.34%	1.41%	1.59%	10.34%	9.50%	7.57%	8.22%	5.85%	4.88%	12.59%	5.69%	3.88%	6.54%	5.58%	8.20%	7.12%	5.94%	13.63%	11.47%
最大值	2.43%	2.68%	2.74%	2.74%	4.98%	3.57%	1.50%	2.33%	2.99%	2.66%	2.33%	1.33%	2.33%	1.43%	2.74%	2.85%	2.99%	2.99%	3.21%	2.33%	3.21%	19.18%	14.64%	14.37%	13.90%	11.38%	10.66%	21.58%	13.77%	6.73%	9.48%	11.56%	16.00%	9.46%	10.78%	24.10%	18.57%
注：中括号[]中数字代表的参考文献分别为：1.蒋尚明等, 2013；2.李希灿等, 2010；3.周佩玲等, 2001；4.崔东文, 2013；5.崔东文等, 2016；6.李佳等, 2008；7.徐纬芳等, 2010；8.花蓓等, 2008；9.金菊良等, 2000.

4.2.2 基于同型规范变换的4种牡丹江市TSP时序预测模型的雅马渡站径流时序预测

由于牡丹江市TSP的4种预测模型只是时间序列的预测模型, 因此, 也只用于建立雅马渡站径流时间序列(k=3)预测模型.

① 雅马渡站径流年均值时序的参照值和规范变换式的设置雅马渡站径流量(C_y)的年均值的时序监测数据c_t的变换式仍如式(12)所示, 径流量的参照值仍设置为c_y0=30, 阈值c_b=100.由式(12)和式(4)计算得到雅马渡站径流样本时序变量(从第4个样本开始)的规范值y_t′见表 7.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值及预测样本的计算输出值将表 7中径流时序变量的规范值y_t′组成的3(k=3)个因子的规范值y_j^′(j=t-1, t-2, t-3)代入3.3.2节牡丹江的TSP预测公式(21)~(27)中, 计算得到两种结构的3种智能预测模型和NV-ULR预测模型前16个建模样本(序号4~19)的模型拟合输出值及后4个检测(预测)样本(序号20^*~23^*)的模型计算输出值亦见表 7.计算得到3种智能预测模型和NV-ULR预测模型的前16个建模样本的模型输出的拟合相对误差绝对值见表 8.

③ 预测样本模型输出的误差修正及修正后的径流量的实际预测值从表 7可见, 分别与牡丹江市TSP时序预测模型的20^*~23^*径流预测样本的4种预测模型输出相似的拟合样本如表 9示.用误差修正公式修正后的4个检测(预测)样本的4种预测模型的输出值Y_x′如表 10所示.再由式(12)和式(4)的逆运算, 计算得到4种预测模型对序号20^*~23^*的径流实际预测值c_yx亦见表 11.表 10和表 11中还分别列出序号20^*~23^*的径流实际值的规范值Y_x₀′和实际值c_y₀.

④ 多种预测模型的实际预测值的相对误差及比较4个检测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)亦见表 12.表 12中还列出直接用3.2.2节基于多因子的雅马渡站径流预测模型(13)~(19)计算得到的预测样本的相对误差r_x.为了比较, 表 12中还列出了16种传统预测模型和方法用于雅马渡站径流预测的相对误差.可以看出, 基于同型规范变换的不同预测变量的预测模型用于雅马渡径流量预测的相对误差绝对值平均值和最大相对误差绝对值均小于或远小于16种传统预测模型和方法预测的相应误差.

4.3 同型规范变换的不同预测变量的预测模型用于牡丹江市TSP时序预测 4.3.1 基于同型规范变换的灞河口COD_Mn预测模型的牡丹江市TSP时序预测

① TSP年均值时序数据参照值和规范变换式的设置牡丹江市TSP年均值的时间序列(1991—2002年)数据仍见文献(陈世权等, 2003).TSP时序数据变换式仍同式(20), 参照值仍设置为c_t0=0.05.由式(20)和式(4)计算得到TSP的规范值x_t′如表 13所示.仍取最近邻时刻数k=3, 则从第4个样本(第4年)的数据规范值起始, 由TSP第t个样本的前3个最近邻时序数据的规范值x_t_-1、x_t_-2、x_t_-3构成第t个样本的3个影响因子, 则全部组成9个时序样本(1994—2002年), 其中, 前7个作为拟合检验样本, 后2个作为预测检验样本.

表 13 4种预测模型的建模样本拟合输出值y′_i及预测样本计算输出值y′_x Table 13 Fitting output value y′_i of modeling sample and calculating output value y′_x of predicting sample based on 4 prediction models

年份序号	基于灞河口COD_Mn预测模型的牡丹江TSP建模样本拟合输出及预测样本计算输出							预测量的规范值y_t0′	基于雅马渡站径流预测模型的牡丹江TSP建模样本的拟合输出及预测计算输出							预测量的规范值y_t0′
年份序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	预测量的规范值y_t0′	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	预测量的规范值y_t0′
4	0.4139	0.4103	0.4077	0.4089	0.3773	0.4712	0.3621	0.4174	0.2489	0.2555	0.2457	0.2449	0.4295	0.4644	0.4015	0.2889
5	0.4000	0.3968	0.3931	0.3942	0.4179	0.4669	0.3543	0.3976	0.3170	0.3248	0.3143	0.3133	0.4713	0.4914	0.4186	0.3219
6	0.3812	0.3784	0.3735	0.3746	0.4084	0.4569	0.3439	0.4062	0.3922	0.4005	0.3909	0.3897	0.5069	0.5198	0.4376	0.3087
7	0.3724	0.3698	0.3643	0.3654	0.4024	0.4508	0.3390	0.4051	0.4200	0.4283	0.4195	0.4182	0.5238	0.5262	0.4448	0.3104
8	0.3688	0.3663	0.3607	0.3617	0.3996	0.4477	0.3371	0.3998	0.4294	0.4377	0.4294	0.4280	0.5276	0.5273	0.4472	0.3187
9	0.3695	0.3670	0.3613	0.3624	0.3973	0.4484	0.3374	0.3943	0.4280	0.4363	0.4279	0.4266	0.5282	0.5273	0.4468	0.3266
10	0.3660	0.3636	0.3578	0.3588	0.3950	0.4447	0.3355	0.2802	0.4359	0.4441	0.4360	0.4347	0.5286	0.5276	0.4489	0.4218
11*	0.3294	0.3278	0.3205	0.3215	0.3420	0.3796	0.3157	0.3035	0.4842	0.4921	0.4869	0.4854	0.5109	0.5171	0.4615	0.4093
12*	0.3010	0.2998	0.2918	0.2926	0.3108	0.3473	0.3004	0.3297	0.5230	0.5304	0.5282	0.5266	0.4978	0.5095	0.4718	0.3920
注：“*”表示预留的预测检验样本.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值及预测样本的计算输出值将计算得到的各因子的规范值x_i′代入3.1.2节灞河口COD_Mn预测公式(5)~(11)中, 计算得到3种智能预测模型和NV-ULR预测模型前7个(1994—2000年)建模样本(样本序号4~10)的模型拟合输出值及后2个(2001^*年、2002^*年)检测(预测)样本(样本序号11^*、12^*)的模型计算输出值, 如表 13所示.同时, 计算得到3种智能预测模型和NV-ULR预测模型的前7个建模样本的模型输出的拟合相对误差绝对值, 如表 14所示.

表 14 4种预测模型的建模样本的拟合相对误差r′_i Table 14 Fitting relative errors of modeling samples based on four prediction models

年份序号	基于COD_Mn预测模型的牡丹江TSP建模样本的拟合相对误差r′_i							基于雅马渡站径流预测模型的牡丹江TSP建模样本的拟合相对误差r′_i
年份序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR
4	0.84%	1.70%	2.32%	2.04%	9.61%	12.89%	13.25%	13.85%	11.56%	14.95%	15.23%	48.67%	60.75%	38.98%
5	0.60%	0.20%	1.13%	0.86%	5.11%	17.43%	10.89%	1.52%	0.90%	2.36%	2.67%	46.41%	52.66%	30.04%
6	6.15%	6.84%	8.05%	7.78%	0.54%	12.48%	15.34%	27.05%	29.74%	26.63%	26.24%	64.20%	68.38%	41.76%
7	8.07%	8.71%	10.07%	9.80%	0.67%	11.28%	16.32%	35.31%	37.98%	35.15%	34.73%	68.75%	69.52%	43.30%
8	7.75%	8.38%	9.78%	9.53%	0.05%	11.98%	15.68%	34.73%	37.34%	34.73%	34.30%	65.55%	65.45%	40.32%
9	6.29%	6.92%	8.37%	8.09%	0.76%	13.72%	14.43%	31.05%	33.59%	31.02%	30.62%	61.72%	61.45%	36.80%
10	30.62%	29.76%	27.69%	28.05%	40.97%	58.71%	19.74%	3.34%	5.29%	3.37%	3.06%	25.32%	25.08%	6.42%

③ 预测样本模型输出的误差修正值及修正后的TSP实际预测值从表 13可见, 分别与TSP时序预测模型的序号11^*、12^*预测样本的4种预测模型输出相似的拟合样本如表 15所示.用误差修正公式修正后的2个检测(预测)样本的4种预测模型的输出值Y_x′如表 16所示.再由式(20)和式(4)的逆运算, 计算得到4种预测模型对序号11^*、12^*TSP的实际预测值c_yx, 如表 17所示.表 16和表 17中还分别列出序号11^*、12^*TSP的实际值的规范值Y_x₀′和实际值c_y₀.

表 15 4种预测模型的预测样本输出的相似样本 Table 15 Similar samples of prediction samples output based on four prediction models

表 16 4种预测模型的预测样本误差修正后的模型输出值 Table 16 Model output values based on the corrected sample error of four prediction models

表 17 4种预测模型的预测样本误差修正后的模型实际预测值 Table 17 Actual predicted values based on the corrected sample error of four prediction models

④ 多种预测模型的实际预测值的相对误差及比较2个检测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)如表 18所示.

表 18 预测样本的多种预测模型的预测相对误差的绝对值及其平均值和最大值r_x Table 18 Absolute values of relative errors, their mean values and maximum values of various prediction models for prediction samples

预测样本序号	基于灞河口COD_Mn模型的牡丹江TSP时序预测样本的相对误差r_x							基于雅马渡站径流模型的牡丹江TSP时序预测样本的相对误差r_x							基于时间序列的牡丹江TSP时序预测样本的相对误差r_x
预测样本序号	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR	NV-FNN(2)	NV-FNN(3)	NV-PPR(2)	NV-PPR(3)	NV-SVR(2)	NV-SVR(3)	NV-ULR
11^*	0.88%	0.44%	0.88%	0.44%	2.19%	2.19%	0.44%	1.75%	1.32%	0.00%	0.00%	4.39%	1.32%	0.44%	0.00%	0.00%	0.44%	0.44%	3.50%	3.50%	0.44%
12^*	1.54%	0.77%	1.15%	0.77%	0.38%	1.54%	1.54%	1.54%	0.38%	3.08%	3.08%	1.54%	4.62%	0.00%	0.77%	1.92%	1.54%	0.38%	0.00%	0.38%	0.77%
平均值	1.21%	0.61%	1.02%	0.61%	1.29%	1.87%	0.99%	1.65%	0.85%	1.54%	1.54%	2.97%	2.97%	0.22%	0.39%	0.96%	0.99%	0.41%	1.75%	1.94%	0.61%
最大值	1.54%	0.77%	1.15%	0.77%	2.19%	2.19%	1.54%	1.75%	1.32%	3.08%	3.08%	4.39%	4.62%	0.44%	0.77%	1.92%	1.54%	0.44%	3.50%	3.50%	0.77%

4.3.2 基于同型规范变换的雅马渡站径流量预测模型的牡丹江市TSP时序预测

① TSP年均值及其影响因子的参照值和规范变换式的设置牡丹江市1991—2002年总悬浮颗粒物(TSP)年均值的时间序列数据仍见文献(陈世权等, 2003).设置如式(28)所示的TSP时序数据变换式.

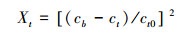
(28)

式中, 参照值c_t₀ =0.05, 阈值c_b=0.615, c_t、c_t₀和c_b的单位相同, 皆为mg·m^-3.

由式(28)和式(4)计算得到TSP的时序规范值x_t′.仍取最近邻时刻数k=3, 则从第4个样本(第4年)的数据规范值起始, 由TSP第t个样本的前3个最近邻时序数据的规范值x_t_-1、x_t_-2、x_t_-3构成第t个样本的3个影响因子, 则全部组成9个时序样本(1994—2002年), 其中, 前7个作为拟合检验样本, 后2个作为预测检验样本.

② 3种智能模型和NV-ULR模型的建模样本拟合输出值y′_i及预测样本的计算输出值y′_x将9个TSP时序样本组成的各因子的规范值x_i′代入3.2.2节雅马渡站径流预测公式(13)~(19)中, 计算得到3种智能预测模型和NV-ULR预测模型前7个(1994—2000年)建模样本(样本序号4~10)的拟合输出值及后2个(2001^*、2002^*)检测(预测)样本(样本序号11^*~12^*)的模型计算输出值见表 13.计算得到3种智能预测模型和NV-ULR预测模型的前7个拟合样本的模型输出的拟合相对误差绝对值见表 14.

③ 预测样本模型输出的误差修正及修正后的TSP的实际预测值从表 13可见, 分别与TSP时序预测模型的序号11^*、12^*预测样本的4种预测模型输出相似的拟合样本见表 15.用误差修正公式修正后的2个检测(预测)样本的4种预测模型的输出值Y_x′亦见表 16.再由式(28)和式(4)的逆运算, 计算得到4种预测模型对序号11^*、12^*TSP的实际预测值c_yx亦见表 17.表 16和表 17中还分别列出序号11^*、12^*TSP的实际值的规范值Y_x₀′和实际值c_y₀.

④ 多种预测模型的实际预测值的相对误差及比较2个检测样本的4种预测模型预测的实际预测值与真实(测定)值之间的相对误差r_x(绝对值)及其平均值和最大相对误差(绝对值)亦见表 18.表 18中还列出直接用3.3.2节基于牡丹江市时序预测模型公式(21)~(27)计算得到的预测样本的相对误差r_x.文献(陈世权等. 2003)用灰色预测法预测得到的平均值和最大值分别为10.34%和14.91%.

4.4 同型规范变换预测模型和传统预测模型的相对误差在不同误差区间所占百分比

具有同型规范变换的3种智能预测模型和NV-ULR预测模型及20种传统预测模型的3个验证实例, 其相对误差绝对值的平均值及最大值在不同误差区间所占百分比如表 19所示.可见, 同型规范变换的不同预测模型预测的相对误差绝对值的平均值几乎都小于3%, 最大相对误差绝对值全都小于5%.而20种传统预测模型预测的相对误差绝对值的平均值全都大于3%, 其中, 误差在[5%, 15%)内的占了85%；最大相对误差绝对值全都大于5%, 其中, 误差在[10%, 30%)内的占了75%.可见, 基于同型规范变换的不同预测模型预测的相对误差绝对值的平均值和最大相对误差绝对值皆小于或远小于所有20种传统预测模型的相应误差.

表 19 同型规范变换的预测模型和传统预测模型的3个验证实例的相对误差绝对值的平均值及最大值在不同误差区间所占百分比 Table 19 Percentage of relative errors of homogeneous normal transform prediction model and traditional prediction model in different error ranges

5 分析与讨论(Analysis and discussion)

从表 6、表 12、表 18和表 19可以看出, 只要将同型规范变换与误差修正相结合, 应用于同一个样本预测, 不仅用同类预测模型, 即使用不同类型预测模型, 比如NV-FNN、NV-PPR、NV-SVR和NV-ULR等, 其预测值及其预测精度(与实际值的相对误差绝对值), 彼此差异皆甚微, 预测值与实际值均十分接近.因此, 可以说具有同型规范变换的不同预测变量的不同类型预测模型之间还具有广义的兼容性、等效性和对称性, 其预测精度比传统预测模型和方法的预测精度高数倍到数10倍.

理论分析和实例验证均表明, 由于具有同型规范变换和误差修正相结合的不同预测模型的实际预测值的相对误差, 与预测变量的影响因子的个数、建模样本个数(样本容量)及预测变量的原始数据分布特征和变化规律, 如线性或非线性、正态或非正态、独立或相关、正向或逆向、趋势性或波动性、快变或缓变等均无关, 也与选取的何种预测模型无关, 因而满足同型规范变换的不同预测量的预测模型之间的兼容性、等效性和对称性是不受条件约束的.兼容性、等效性和对称性的重要意义在于：无论是多因子或时间序列的预测问题, 只要对某预测变量建立了基于规范变换的某种智能预测模型、统计预测模型或其它非机理性预测模型, 都可以将建立的基于规范变换的该预测变量的预测模型, 结合误差修正法, 直接用于具有同型规范变换的其它任意预测变量的预测, 而无需了解其它预测变量的样本个数、影响因子个数及数据分布和变化规律等特性.

由于传统的预测模型对预测变量及其影响因子的变换皆是彼此独立无关的变换, 因而对因子数不同的预测问题, 模型的结构不能简化和统一, 而且不同预测变量变换后的数据分布特性和变化规律也不可能变得一致或相似.因此, 不同预测变量的传统预测模型之间不具有兼容性、等效性和对称性.这正是基于规范变换尤其是同型规范变换的预测模型与传统的预测模型的显著不同之处.

从理论上讲, 满足同型规范变换的不同预测变量的预测模型之间具有的兼容性、等效性和对称性不受的预测模型的限制, 但本文仅对投影寻踪、支持向量机、前向神经网络(比如双极性前向网络、BP网络、RBF网络、概率神经网络等)等智能预测模型和统计预测模型等非机理性预测模型的兼容性、等效性和对称性进行了理论论证和实例验证, 对机理性预测模型是否成立还有待深入研究.

6 结论(Conclusions)

本文虽然只对具有同型规范变换n_j=2的不同预测变量的预测模型的兼容性、等效性和对称性进行了实例验证, 而理论已证明具有同型规范变换n_j=1或n_j=0.5的不同预测变量的预测模型也同样具有兼容性、等效性和对称性.由于预测变量的同型规范变换只有n_j=2、1或0.5这3种不同的类型, 故通常只需建立3种不同的同型规范变换的预测量的预测模型, 即可满足一切预测问题的需要, 从而既省时, 又省力, 给实际应用带来了极大方便.因而同型规范变换的预测变量的预测模型的兼容性、等效性和对称性的发现, 不仅具有重要理论意义, 而且具有重要的实用价值.

参考文献

陈世权, 贲毅, 宋居可, 等. 2003. 牡丹江市区大气总悬浮颗粒物污染趋势及预测[J]. 黑龙江环境通报, 27(2): 64-65.

Chen S Y, Xue Z C, Li M. 2013. Variable sets principle and method for flood classification[J]. Science China Technological Sciences, 56(9): 2343-2348. DOI:10.1007/s11431-013-5304-4

Comrie A C. 2013. Comparing neural networks and regression models for ozone forecasting[J]. Journal of the Air & Water Mangement Association, 47(6): 653-663.

崔东文. 2013. 多隐层BP神经网络模型在径流预测中的应用[J]. 水文, 33(1): 68-73.

崔东文, 金波. 2016. 鸟群算法-投影寻踪回归模型在多元变量年径流预测中的应用[J]. 人民珠江, 37(11): 26-30. DOI:10.3969/j.issn.1001-9235.2016.11.006

笪英云, 汪晓东, 赵永刚, 等. 2015. 基于关联向量机回归的水值预测模型[J]. 环境科学学报, 35(11): 3730-3735.

房平, 邵瑞华, 司全印, 等. 2011. 最小二乘支持向量机应用于西安霸河口水质预测[J]. 系统工程, (6): 113-117. DOI:10.3969/j.issn.1001-2362.2011.06.051

Fu T C. 2011. A review on time series data mining[J]. Engineering Application Artificial Intelligence, 24(1): 164-181. DOI:10.1016/j.engappai.2010.09.007

花蓓, 熊伟, 陈华. 2008. 模糊支持向量机在径流预测中的应用[J]. 武汉大学学报(工程版), 41(1): 5-8.

金菊良, 杨晓华, 金保明, 等. 2000. 门限回归模型在年径流预测中的应用[J]. 冰川冻土, 22(3): 230-234. DOI:10.3969/j.issn.1000-0240.2000.03.007

蒋尚明, 金菊良, 袁先江, 等. 2013. 基于近邻估计的年径流预测动态联系数回归模型[J]. 水利水电技术, 44(7): 5-9. DOI:10.3969/j.issn.1000-0860.2013.07.002

李佳, 王黎, 马光文, 等. 2008. LS-SVM在径流预测中的应用[J]. 中国农村水利水电, (5): 8-10, 14.

李希灿, 王静, 赵庚星. 2010. 径流中长期预报模糊识别优化模型及应用[J]. 数学的实践与认识, 40(6): 92-98.

李祚泳, 汪嘉杨, 徐源蔚. 2018. 基于规范变换与误差修正的回归支持向量机的环境系统预测[J]. 环境科学学报, 38(3): 1235-1244.

李祚泳, 汪嘉杨, 徐源蔚. 2019a. 规范变换与误差修正结合的环境系统的前向网络和投影寻踪预测模型[J]. 环境科学学报, 39(6): 2053-2070.

李祚泳, 魏小梅, 汪嘉杨. 2019b. 规范变换降维与误差修正结合的环境系统的一元线性回归预测[J]. 环境科学学报, 39(7): 2455-2466.

Liu Y H, Zhu Q, Yao D, et al. 2015. Forecasting urban air quality via a back-propagation neural network and a selection sample rule[J]. Atmosphere, 6(7): 891-907. DOI:10.3390/atmos6070891

Moazami S, Noori R, Amiri B J, et al. 2016. Reliable prediction of carbon monoxide using development support vector machine[J]. Atmospheric Pollution Research, 7(3): 412-418. DOI:10.1016/j.apr.2015.10.022

孙宝磊, 孙蒿, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 37(5): 1864-1871.

Shaban K B, Kadri A, Rezk E, et al. 2016. Urban air pollution monitoring system with forecasting models[J]. IEEE Sensors Journal, 16(8): 2598-2606. DOI:10.1109/JSEN.2016.2514378

Tan G H, Yan J Z, Gao C, et al. 2012. Prediction of water quality time series data based on least squares support vector machine[J]. Procedia Engineering, 31: 1194-1199. DOI:10.1016/j.proeng.2012.01.1162

Thoe W, Wong S H C, Choo K W, et al. 2012. Daily prediction of marine beach water quality in Hong Kong[J]. Journal of Hydro-environment Research, 6(3): 164-180. DOI:10.1016/j.jher.2012.05.003

王保良, 范昊, 冀海峰, 等. 2016. 基于分段线性表示的最近邻的水质预测方法[J]. 环境工程学报, 10(2): 1005-1009.

Xi J H, Wang H D, Jiang L Y. 2012. Multivariate time series prediction based on a simple RBF network[J]. Advanced Material Research, 566: 97-102. DOI:10.4028/www.scientific.net/AMR.566.97

徐纬芳, 刘成忠, 顾延涛. 2010. 基于PCA和支持向量机的径流预测应用研究[J]. 水资源与水工程学报, 21(6): 72-75.

周佩玲, 陶小丽, 傅忠谦, 等. 2011. 基于遗传算法的RBF网络及应用[J]. 信号处理, 17(3): 269-273.

张旭东, 高茂亭. 2016. 基于IGA-BP网络的水质预测方法[J]. 环境工程学报, 10(3): 1566-1761.


环境科学学报 2020, Vol. 40 Issue (4): 1517-1534