2. 南京大学地球科学与工程学院, 南京 210023
2. School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023
我国西南岩溶地下暗河(管道)常常很难进入直接调查, 定量示踪试验是表征岩溶地下河污染物运移的有效手段, 它不仅能确定两点之间的水力联系, 还能通过穿透曲线(即示踪剂浓度-时间曲线)反映岩溶含水层中的污染物运移过程(Goldscheider et al., 2008).野外监测到的穿透曲线(BTC)常呈明显拖尾特征, 但传统一维对流弥散方程很难模拟这种现象, 因此, 大量研究在对流弥散方程中增加暂时存储过程项, 得到新的数值拟合方法(Bencala et al., 1983; Field et al., 2000; 2014;Hauns et al., 2001; Massei et al., 2006; Li, 2009; Morales et al., 2010).模拟长拖尾的一种常见方法是沿着岩溶管道设置存储区或“死水区”, 相应的方法称为暂时存储模型(Bencala et al., 1983)和两区模型(Field et al., 2000).模型假设这些存储区内水体相对于流体的纵向流动是停滞的, 并且服从一级传质交换关系, 即主流通道与存储区之间的溶质交换量与两者的浓度差成正比.因此, 上述两种模型的共同概念基础为研究对象中水流被划分为流动区域水体和非流动区域水体, 可称为“死区模型”.“死区模型”概念自提出以来(Aris, 1959; Coats et al., 1964), 被很多学者改进后广泛应用于各种含水介质的运移研究.Thackston等(1970)、Valentine等(1977; 1979)、Nordin等(1980)、Bencala等(1983)和Runkel等(1993)研究了适用于明渠流的两区非平衡模型, 即暂时存储模型(Transient storage model, TSM).Van Genuchten等(1976; 1977)、De Smedt等(1979)将其应用于土壤中非饱和带及饱和带的溶质运移, 随后Lassey等(1988)、Van Genuchten等(1989)推导出具有一阶衰减的两位点/两区模型解析解, 但没有考虑零阶生成项, 并且将解限制在零初始浓度分布, Toride等(1993)推导了土壤系统中带有一阶衰减和零阶生成项的一维非平衡溶质运移模型的一系列解析解, 包括两位点吸附非平衡模型(Two-site nonequilibrium model)和两区非平衡模型(Two-region nonequilibrium model).Raven等(1988)将两区非平衡模型用于模拟解释片麻岩单裂隙的示踪试验结果.Małoszewski等(1990)推导并测试了适用于裂缝型碳酸盐岩含水层的两区非平衡模型, Belov等(1995)导出一个与两区模型近似的岩溶管道模型, 上述两种模型均强调基质扩散的重要性.本文主要研究块状灰岩中主要活跃岩溶管道的流动问题, 主要的活跃岩溶管道往往具有较大的管道直径, 因此表面积小、湍流速度快, 使得基质扩散可以忽略不计.不考虑岩溶管道周围基质扩散, Field等(2000)根据多孔介质中两区非平衡模型方程(Toride, 1993)修改得到包括溶质一阶衰减和溶质吸附到管壁过程的流动区和非流动区溶质运移方程, 简称两区模型(Two-region nonequilibrium model, TRM), 并将该模型系统应用于岩溶管道的溶质运移研究.两区模型定义流动区和非流动区, 近年来已被广泛用于岩溶管道溶质运移研究(Field et al., 2000; Geyer et al., 2007; Göppert et al., 2008; Goldscheider, 2008; Magal et al., 2013; Zhao et al., 2017);暂时存储模型(Transient storage model, TSM)定义主通道和存储区, 也被用于岩溶地下河污染物运移研究(郭芳等, 2016; Dewaide et al., 2016; Zhao et al., 2019).但同时使用这两个模型模拟穿透曲线并进行对比的研究较少, 且两个模型的对比研究也不多见, 以致模型选取面临一定困难, 因此, 本文重点探讨这两个模型的异同点, 以期为模型的正确选取提供重要依据.
2 概念模型对比(Comparison of models) 2.1 两区模型(TRM)Aris(1959)较早提出管道中“死水区”的概念并探讨了“死水区”对管道水流纵向弥散作用的影响, 之后被用于岩溶含水层介质.Belov等(1995)导出与两区(流动-非流动区)非平衡模型(TRM)类似的岩溶地下河运移模型, 并重点关注了管道周围基质扩散的影响.岩溶地下河管道中发育各种不规则结构, 溶质在溶谭、管道崩塌障碍物、粗糙管壁、弯曲管道、死端分支管道和周围基质岩块等结构中暂时性滞留并随着时间缓慢释放到主通道中(Field et al., 2000; Hauns et al., 2001; Li et al., 2008), 该管道结构内流速明显低于管道中心紊流区(流动区)流速, 可视为非流动区(图 1), 因此, 岩溶地下河溶质运移过程基本符合两区模型的概念基础(图 2).两区模型假设非流动区水体沿着溶质运移路径均匀分布, 流动区和非流动区之间发生溶质交换, 对流弥散过程只在流动区中发生, 溶质在非流动区内瞬时完成均匀分布, 流动区和非流动区内都可能发生化学反应, 如吸附和一阶衰减.Field等(2000)首次系统性证明不考虑基质扩散的两区模型适用于岩溶地下河溶质运移研究并能解释穿透曲线的明显拖尾.假设注入示踪剂为保守型溶液, 则不考虑化学反应, 忽略示踪剂吸附和衰减作用, 溶质运移过程主要包括对流、弥散和溶质交换, 模型方程见式(1)~(2)(Toride et al., 1993; Field et al., 2000).
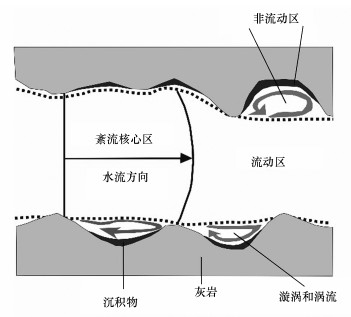 |
| 图 1 岩溶地下河几何结构和水流示意图(Geyer et al., 2007) Fig. 1 Conceptual model of the geometry and the flow within a karst conduit |
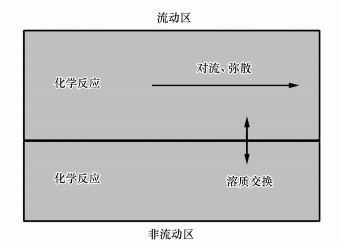 |
| 图 2 两区模型概念示意图 Fig. 2 Conceptual model for two-region nonequilibrium model |
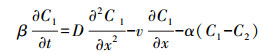
|
(1) |
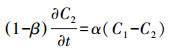
|
(2) |
式中, t为时间(s);x为注入点下游距离(m);C1和C2分别为流动区和非流动区浓度(g·L-1);v为平均流速(m·s-1);D为弥散系数(m2·s-1);α为传质系数(s-1), 表示流动区和非流动区的溶质交换速率;β为分配系数, 表示流动区比例.
2.2 暂时存储模型(TSM)在两区非平衡模型的基础上, 相关研究得到适用于明渠流的暂时存储模型(TSM), 该模型最初用于河流溶质运移和去向的描述(Thackston et al., 1970; Valentine et al., 1977; 1979; Nordin et al., 1980; Bencala et al., 1983; Runkel et al., 1993).在河流中, 主要发生溶质对流和弥散的区域为主通道;导致溶质暂时性存储的区域(滞水区和河床多孔区, 图 3)为暂时存储区.岩溶地下河溶质运移过程(图 1)与地表河(图 3)近似, 符合模型的概念基础(图 4)(Runkel, 1998).在主通道中, 溶质通过对流弥散向下游运移.存储区中不包含对流和弥散过程, 忽略下游运移.侧向入流表示流入主通道的水, 如坡面流、壤中流和地下水排泄.侧向出流表示从主通道流到周围流域的水.主通道和存储区内都可能发生化学反应, 如吸附和一阶衰减.对于保守型溶质, 不考虑化学反应, 忽略侧向入流出流项, 主通道和存储区的质量守恒方程见式(3)~(4)(Bencala et al., 1983).
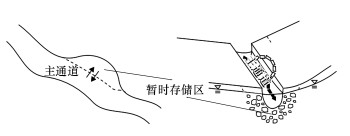 |
| 图 3 河流中溶质暂时性存储机理 Fig. 3 Transient storage mechanisms for a stream |
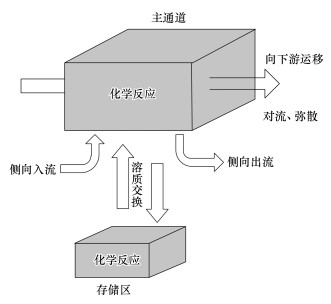 |
| 图 4 暂时存储模型概念示意图(Runkel, 1998) Fig. 4 Conceptual model that includes the main channel and the storage zone |
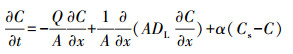
|
(3) |
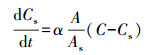
|
(4) |
式中, t为时间(s);x为注入点下游距离(m);C和Cs分别为主通道和存储区中溶质浓度(g·L-1);A和As分别为主通道和存储区的截面积(m2);Q为体积流量(m3·s-1);DL为弥散系数(m2·s-1);α为存储区交换系数(s-1).
2.3 概念模型对比TRM和TSM中, 相对流动区或主通道水流, 非流动区或存储区中的水近似为静止不动.在流动区或主通道中, 溶质通过对流弥散向下游运移;非流动区或存储区中不包含对流弥散过程, 溶质暂时性存储在其中, 且溶质瞬时完成均匀分布.两种模型中两区间的溶质交换均为一阶质量传递过程, 溶质交换仅仅由浓度差和传质/交换系数决定, 传质/交换系数表征溶质交换强度.两种模型的物理意义相近, 对管道示踪实验曲线的拟合效果都很好(R2>0.997)(Zhao et al., 2019).但与TRM不同, TSM包含侧向入流和出流过程.TRM采用分配系数表示流动区和非流动区的比例关系, 而TSM采用主通道截面积和存储区截面积表征主通道和存储区的比例关系.采用TSM可以估计存储区的横截面积、存储区内溶质浓度和交换系数, 而采用TRM只能获得存储区所占比例、存储区内溶质浓度和传质系数.
2.4 模型应用的优缺点两种模型最大的优势和缺点是其简单的概念基础.简化的方程和较少的参数, 使两区模型(TRM)和暂时存储模型(TSM)成为广泛采用的模型.但严格来说, “死区模型”(两区模型和暂时存储模型)不是对岩溶地下河溶质运移过程的物理描述, 因为很难设想一种线性物理驱动机制, 在主河道和存储区之间运移溶质, 在整个存储区均匀分布溶质, 同时阻止存储区纵向移动.但在野外岩溶地下水示踪试验中观测到了严重的示踪拖尾.溶质质量在溶质脉冲上升阶段被移除, 暂时存储在存储区中, 直到溶质脉冲通过, 返回到岩溶地下河中.据此推断, 存在一种机制表现为沿岩溶地下河的溶质质量的暂时性存储.所以可以用“死区模型”方程对观测到的“暂时性存储”现象进行近似模拟.野外岩溶地下河死水区的物理描述与观测到的暂时性存储现象的模拟结果之间的区别对于模型参数的确定和解释至关重要.但当岩溶地下河溶质运移的复杂物理过程与模型的简单概念基础相差较大时, 模型的适用性遭到挑战.TRM假设非流动区沿着整个水流系统连续均匀分布, 采用同一参数描述非流动区存储项.该模型把滞留时间不同的多个非流动区概化成同一区域, 在非流动区离散分布且差异明显的岩溶地下河中存在一定缺陷.基于此, Morales等(2010)提出新模型, 研究溶质在局部死端区的滞留现象.但该模型只适用于整体发育良好, 只是局部区域存在非流动区的岩溶地下河.TSM也无法识别不同性质的暂时存储过程.因此, Choi等(2000)提出包含两个不同存储区的TSM, 该模型被广泛用于地表和地下暂时性储存过程的区分(Harvey et al., 2005; Marion et al., 2008; Zaramella et al., 2016).TSM假定滞留时间符合指数分布, 能拟合短时间交换尺度的穿透曲线, 但不适用交换时间尺度较长的存储过程, 因此, 大量研究采用新的滞留时间分布描述主通道和存储区的溶质交换过程, 如对数正态分布(Wörman et al., 2002)和幂律分布(Haggerty et al., 2002; Gooseff et al., 2003).尽管两种模型方法都能良好拟合观测数据, 但目前没有研究赋予模型参数实际的物理意义, 模型参数无法推广应用到其他岩溶地下河.在参数校正过程中, 无法通过物理意义限制其取值范围, 增加了模型不确定性.两种模型均适用于单轴岩溶地下河, 在岩溶分支地下河中的应用存在一定缺陷.
3 参数对比(Comparison of parameters) 3.1 参数校正过程作者已通过室内示踪实验(Zhao et al., 2019)获取两种水箱-管道结构(对称水箱和不对称水箱)的穿透曲线并采用两种模型较好拟合了实验结果(R2>0.997), 研究区见图 5.示踪剂注入时间为1 s左右, 可近似为瞬时注入.在CXTFIT中(Toride et al., 1999)完成两区模型方程解析解对实测曲线的最优化拟合, 模拟段为从示踪剂注入点到出口的长度.采用OTIS软件(Runkel, 1998)对暂时存储模型的溶质运移方程进行数值求解并拟合实测曲线, 模拟段为取样点1到取样点2.CXTFIT提供两区模型方程在不同输入函数下的解析解, 某一点的连续浓度曲线可近似处理为多脉冲注入边界条件, 作为下游河段的上游边界条件(Ender et al., 2018), 因此可对岩溶地下河运移过程分段进行模拟, 不同阶段的参数不同;而OTIS提供暂时存储模型方程的数值解, 以上游段的出口浓度曲线作为下游段的入口浓度曲线, 也能分段进行模拟.两种模型均只取一段进行模拟研究, 但研究段长度不同.
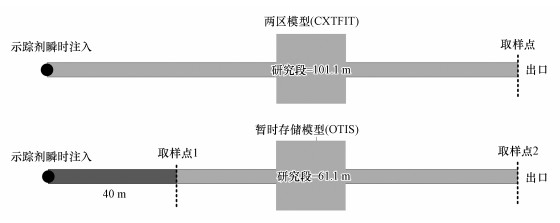 |
| 图 5 两种模型研究段 Fig. 5 Study reach in two modeling tools |
CXTFIT通过Levenberg-Marquardt非线性最小二乘法最小化模拟值与实测值的残差平方和, 校正获得4个参数:v、D、β和ω(αx/v, 其中x为101.1 m).在模拟过程中保持示踪剂注入浓度Ci固定不变且等于RTM/Q(RT为示踪剂回收率, M为注入示踪剂质量, Q为管道流量).为了加速最优拟合的实现, 赋予校正参数合理的初始值.v的初始估计值设定为,v, β的初始估计值设定为β=v/vp(v为平均流速, 采用Qtracer软件分析穿透曲线得到;vp为峰值浓度对应流速), ω的初始估计值通常难以给定, 同时由于ω实际上未知, 在模型校准过程中不能对其施加适当的物理约束, 从而增加了模型的不确定性.最后计算传质系数α=vω/x, 流动区水体弥散系数Dm=D/β和流动区平均流速vm=v/β.
OTIS-P模型(反演模型)将OTIS模型同STARPAC非线性最小二乘法进行耦合.首先在OTIS中通过手动不断尝试(正演)的方法初步估计溶质运移参数, 合理估计参数的初始值将加速这一过程的实现.A的初始值可以通过岩溶管道的实测截面积获得, 但不流动区域的横截面积(As)和交换系数(α)初始值难以确定, 通常通过模型拟合BTC得到, 并且由于实际上未知, 在模型校准过程中不能对其施加适当的物理约束, 从而增加了模型的不确定性.当模拟值同实测值的拟合大致匹配, 再通过OTIS-P自动调参, 实现对实测曲线的最优拟合, 得到参数A、As、DL和α, 最后计算死端区比例(ε=As/A)、存储区滞留时间(T=ε/α)和暂时存储运移时间比例(Fmed200)(Runkel, 2002).Fmed200定量化相对于对流运移, 进入存储区的溶质运移比例:
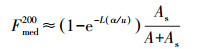
|
(5) |
两种模型的主要溶质运移参数见表 1.岩溶地下河中间紊流核心区在模型中体现为流动区或主通道, vm和u的物理意义近似, 表示流动区(主通道)的平均流速;Dm和DL表示流动区(主通道)的弥散系数.非流动区(存储区)是由于岩溶地下河表面不规则结构而沿着流动边缘形成的漩涡的结果(Valentine et al., 1977; 1979; Rouse, 1946).岩溶地下河的表面不规则结构为凹坑、底切、沿裂缝和层理面不连续的溶解作用、地质构造和崩塌(Ford et al., 1989).导致凹坑形成的湍流漩涡也会导致非流动区(White, 1988).水流流进流出地下河管道汇合口, 随之产生漩涡, 导致非流动区.水跃和管径的突变将促进漩涡的发展(Rouse, 1946)和沉积物的沉积.沉积物尤其在河曲内侧, 形成非流动区.死端通道和垮塌障碍物会造成巨大的水流障碍, 导致大量的不动水体.由漩涡形成的非流动区域, 小于由流体流向管道汇合口、死端通道和其他物理障碍物所形成的非流动区, 但从数学上讲, 效果是相似的, 均可以视作非流动区.溶质在流动区和非流动区之间的运移交换速率由浓度差和α决定, α在两种模型中均表示两区间的溶质交换强度, 其大小与漩涡的数量和湍流强度有关;β表示流动区比例, ε表示非流动区比例, 两者物理意义相反;ω值下降说明非流动区对拖尾的影响程度降低, Fmed200值下降说明存储区对下游溶质运移的影响程度降低, 两者物理意义近似.
| 表 1 主要模型参数 Table 1 Main model parameters |
尽管两个模型参数的物理意义近似, 但参数对溶质运移过程的作用不同.为了调查模拟结果对参数变化的敏感性, 选取中间流速(Q=1293 L·s-1)模拟结果, 在最优参数上下一定范围内调整参数值, 得到对应的穿透曲线(图 6和7).调整参数后的曲线同初始模拟曲线的偏差从视觉上直观判断, 也可通过决定系数(R2)进行判断.考虑到两种模型的初始模拟效果较好(R2>0.997), R2低于0.980表示明显偏差(Dewaide et al., 2016).敏感性分析除了评价参数敏感性, 也表明参数变化对穿透曲线形状(如拖尾)的影响.
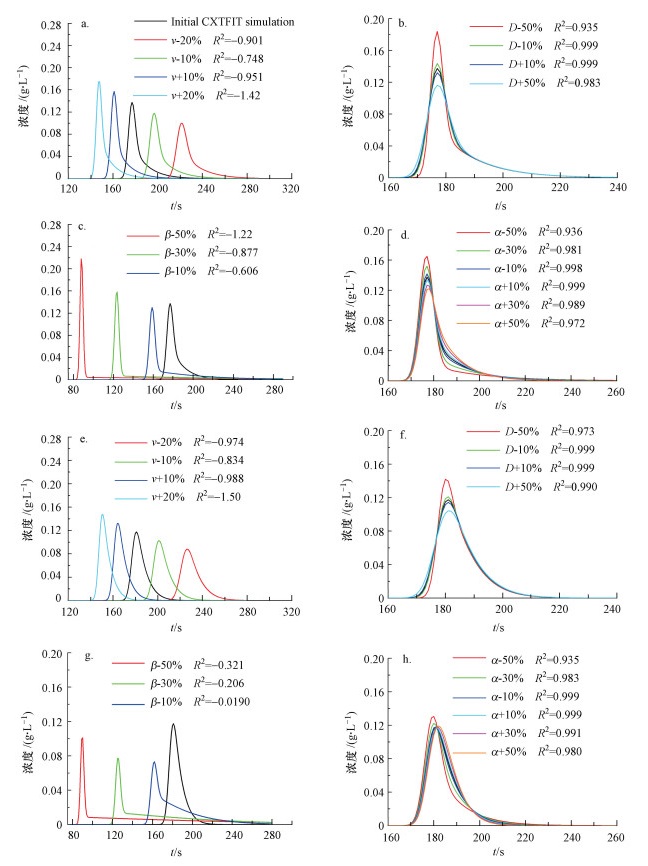 |
| 图 6 两区模型参数敏感度分析(a~d.对称水箱;e~h.不对称水箱;Q=0.1293 L·d-1) Fig. 6 Sensitivity analysis of parameters for TRM |
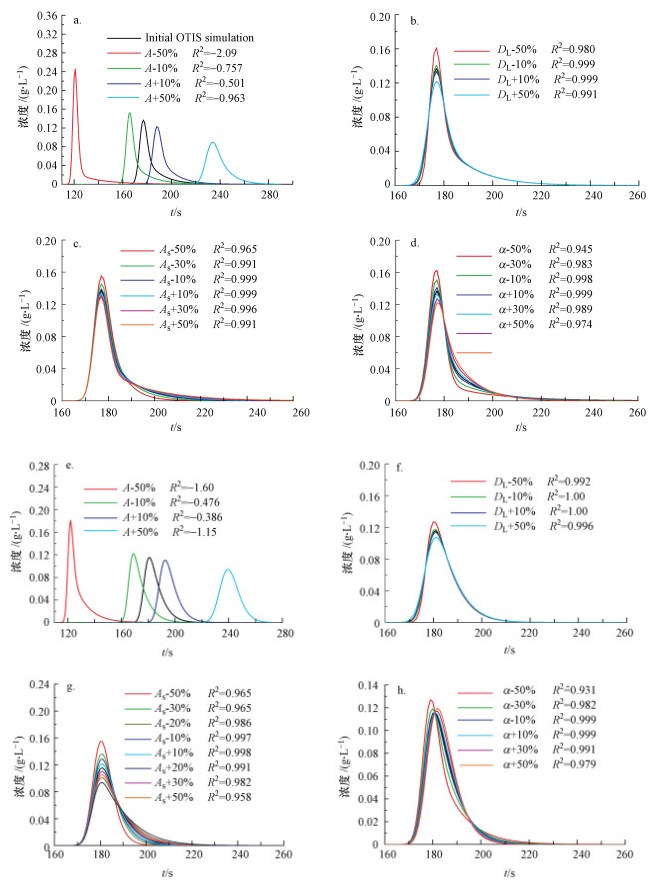 |
| 图 7 暂时存储模型参数敏感度测试(a~d.对称水箱;e~h.不对称水箱;Q=0.1293 L·s-1) Fig. 7 Sensitivity analysis of parameters for TSM |
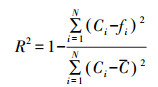
|
(6) |
式中, Ci和fi分别为初始模拟曲线和参数变化后的曲线数据, C为初始模拟曲线浓度数据的平均值.R2值越接近1说明调整参数后的曲线越接近初始模拟曲线, 当调整参数后的曲线与初始模拟曲线数据序列偏差较大时, R2有可能为负值.
3.3.1 两区模型模拟结果对分配系数(β)和平均流速(v)的变化高度敏感, 对弥散系数(D)和传质系数(α)的变化较不敏感.β值表示流动区所占比例, 应该小于1, 因此, 只测试模拟结果对于β降低的敏感性.v的增大或降低使整条曲线发生左右偏移, 曲线变得更加“瘦高”或“矮胖”(图 6a, 6e), β的变化导致穿透曲线向左偏移, 形状变化明显(图 6c, 6g).v变化10%、β降低10%导致R2变为负值, 表明β和v值有较高的可信度.D的变化主要影响曲线宽度和峰值浓度(图 6b, 6f), α的变化主要影响峰值浓度和曲线拖尾(图 6d, 6h), D和α的变化幅度超过50%时, 才能看到偏离模拟曲线的明显变化(R2 < 0.98), 说明这两个参数可靠性相对较低.
v的变化主要影响曲线的峰值浓度和峰值时间, 但对曲线拖尾无显著影响.D的变化可改变峰值浓度, 但对曲线拖尾的影响不明显.β值的降低导致峰值时间的提前和拖尾的显著增长.α值的降低导致拖尾增长, 反之亦然.在“α-50%”曲线中, 拖尾异常明显.两种水箱中α值的降低都导致峰值浓度的升高.当α值增大时, 对称水箱的峰值浓度逐渐下降, 不对称水箱的峰值浓度先下降后升高.
3.3.2 暂时存储模型主通道截面积(A)对拟合曲线有很强的控制作用(图 7a, 7e).改变A的10%时, 拟合曲线整体有明显的左右偏移, 峰值浓度变化明显.表明A的准确性较高, 误差小于校正值的10%.As的敏感度相对较低, 不对称水箱中, 变化30%才能看到新的曲线与初始拟合曲线有明显偏离(图 7g);对称水箱中, 至少需要变化As校正值的50%, 才能看到与初始曲线的明显偏离(图 7c).As和交换系数(α)的变化主要影响曲线的峰值浓度和拖尾(图 7c、7d、7g、7h), α的变化幅度超过30%才能导致与初始拟合曲线的明显偏离.弥散系数(DL)的变化主要影响曲线的峰值浓度, 但敏感度较低(图 7b、7f), DL的变化幅度高达50%仍然没有导致R2降到0.980以下.
A的降低导致拖尾增加, 峰值浓度升高, 曲线的宽度变窄, 反之亦然.A降低至初始值的50%时, 曲线强烈不对称;A增加50%时, 曲线趋向于对称.DL的变化对拖尾没有实质影响.随着As增大, 曲线拖尾程度逐渐增长, 峰值浓度逐渐降低.在“As+50%”曲线中, 拖尾异常显著.α值的降低导致拖尾增长, 反之亦然.α降低50%后, 曲线明显不对称.两种水箱中α的降低都导致峰值浓度增大, α的增大导致对称水箱峰值浓度的降低和不对称水箱峰值浓度的升高.
4 结论(Conclusions)1) 两区模型(TRM)和暂时存储模型(TSM)最大的优势和缺点为两数值模型简单的概念基础.虽然岩溶地下河溶质运移的物理驱动机制与模型假设不完全相符, 但通过模型的暂时存储机制近似表征复杂的溶质运移物理过程是可行的, 采用模型方程可模拟观测到的溶质“暂时性存储”现象.简化的方程和较少的参数使其成为被广泛采用的模型, 但两种模型把溶质滞留时间不同的多个区域概化成同一性质的非流动区或存储区, 存在一定缺陷.
2) 在CXTFIT软件中获得TRM的解析解, 而OTIS软件提供TSM的数值解.OTIS和CXTFIT软件均能通过管道中不同观测点的穿透曲线分段表征不同阶段管道的溶质运移过程.两模型中溶质运移过程和表征参数的物理意义近似, 都能较好拟合管道溶质运移曲线.采用TSM可以校正得到暂时存储区的横截面积, 但采用TRM只能获得存储区的比例.
3) 两模型的弥散系数和交换系数的敏感度较低.两区模型的模拟结果对分配系数和平均流速的变化高度敏感;暂时存储模型的模拟结果对主通道截面积的变化高度敏感, 存储区截面积的敏感度相对较低.两区模型中, 平均流速和弥散系数的变化对拖尾无显著影响;暂时存储模型中, 弥散系数的变化对拖尾无显著影响.
Aris R. 1959. The longitudinal diffusion coefficient in flow through a tube with stagnant pockets[J]. Chemical Engineering Science, 11(3): 194-198. |
Belov A P, Atkinson T C.1995.Non-Fickian Tracer Dispersion in a karst Conduit Embedded in a Porous Medium Medium//Wrobel L C, Latinopoulos P.Third International Conference on Water Pollution: Modelling, Measuring and Prediction[M].London: Computational Mechanics Publications.105-112
|
Bencala K E, Walters R A. 1983. Simulation of solute transport in a mountain pool-and-riffle stream:a transient storage model[J]. Water Resources Research, 19(3): 718-724. DOI:10.1029/WR019i003p00718 |
Choi J, Harvey J W, Conklin M H. 2000. Characterizing multiple timescales of stream and storage zone interaction that affect solute fate and transport in streams[J]. Water Resources Research, 36(6): 1511-1518. DOI:10.1029/2000WR900051 |
Coats K H, Smith B D. 1964. Dead end pore volume and dispersion in porous media[J]. Society of Petroleum Engineers Journal, 4: 73-84. DOI:10.2118/647-PA |
De Smedt F, Wierenga P J. 1979. Mass transfer in porous media with immobile water[J]. Journal of Hydrology, 41(1/2): 59-67. |
Dewaide L, Bonniver I, Rochez G, et al. 2016. Solute transport in heterogeneous karst systems:Dimensioning and estimation of the transport parameters via multi-sampling tracer-tests modelling using the OTIS (one-dimensional transport with inflow and storage) program[J]. Journal of Hydrology, 534: 567-578. DOI:10.1016/j.jhydrol.2016.01.049 |
Ender A, Goeppert N, Goldscheider N. 2018. Spatial resolution of transport parameters in a subtropical karst conduit system during dry and wet seasons[J]. Hydrogeology Journal, 26(7): 2241-2255. DOI:10.1007/s10040-018-1746-x |
Field M S, Pinsky P F. 2000. A two-region nonequilibrium model for solute transport in solution conduits in karstic aquifers[J]. Journal of Contaminant Hydrology, 44(3): 329-341. |
Field M S, Leij F J. 2014. Combined physical and chemical nonequilibrium transport model for solution conduits[J]. Journal of Contaminant Hydrology, 157: 37-46. DOI:10.1016/j.jconhyd.2013.11.001 |
Geyer T, Birk S, Licha T, et al. 2007. Multitracer test approach to characterize reactive transport in Karst aquifers[J]. Groundwater, 45(1): 36-45. DOI:10.1111/j.1745-6584.2006.00261.x |
Göppert N, Goldscheider N. 2008. Solute and colloid transport in karst conduits under low-and high-flow conditions[J]. Groundwater, 46(1): 61-68. |
Goldscheider N. 2008. A new quantitative interpretation of the long-tail and plateau-like breakthrough curves from tracer tests in the artesian karst aquifer of Stuttgart, Germany[J]. Hydrogeology Journal, 16(7): 1311-1317. DOI:10.1007/s10040-008-0307-0 |
Goldscheider N, Meiman J, Pronk M, et al. 2008. Tracer tests in karst hydrogeology and speleology[J]. International Journal of speleology, 37(1): 27-40. DOI:10.5038/1827-806X.37.1.3 |
Gooseff M N, Wondzell S M, Haggerty R, et al. 2003. Comparing transient storage modeling and residence time distribution (RTD) analysis in geomorphically varied reaches in the Lookout Creek basin, Oregon, USA[J]. Advances in Water Resources, 26(9): 925-937. DOI:10.1016/S0309-1708(03)00105-2 |
郭芳, 姜光辉, 于奭, 等. 2016. 地下河不同流量状态下溶质运移的参数及模拟[J]. 南京大学学报(自然科学), 52(3): 496-502. |
Haggerty R, Wondzell S M, Johnson M A. 2002. Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream[J]. Geophysical Research Letters, 29(13): 181-184. |
Harvey J W, Saiers J E, Newlin J T. 2005. Solute transport and storage mechanisms in wetlands of the Everglades, south Florida[J]. Water Resources Research, 41(5): 247-254. |
Hauns M, Jeannin P Y, Atteia O. 2001. Dispersion, retardation and scale effect in tracer breakthrough curves in karst conduits[J]. Journal of Hydrology, 241(3): 177-193. |
Lassey K R. 1988. Unidimensional solute transport incorporating equilibrium and rate-limited isotherms with first-order loss:1.Model conceptualizations and analytic solutions[J]. Water Resources Research, 24(3): 343-350. DOI:10.1029/WR024i003p00343 |
Li G, Loper D E, Kung R. 2008. Contaminant sequestration in karstic aquifers:Experiments and quantification[J]. Water Resources Research, 44: W02429. |
Li G. 2009. Analytical solution of advective mixing in a conduit[J]. Groundwater, 47(5): 714-722. DOI:10.1111/j.1745-6584.2009.00575.x |
Magal E, Arbel Y, Caspi S, et al. 2013. Determination of pollution and recovery time of karst springs, an example from a carbonate aquifer in Israel[J]. Journal of Contaminant Hydrology, 145: 26-36. DOI:10.1016/j.jconhyd.2012.10.010 |
Maloszewski P, Zuber A. 1990. Mathematical modeling of tracer behavior in short-term experiments in fissured rocks[J]. Water Resources Research, 26(7): 1517-1528. DOI:10.1029/WR026i007p01517 |
Marion A, Zaramella M, Bottacin-Busolin A. 2008. Solute transport in rivers with multiple storage zones:The STIR model[J]. Water Resources Research, 44(10): 440-445. |
Massei N, Wang H Q, Field M S, et al. 2006. Interpreting tracer breakthrough tailing in a conduit-dominated karstic aquifer[J]. Hydrogeology Journal, 14(6): 849-858. DOI:10.1007/s10040-005-0010-3 |
Morales T, Uriarte J A, Olazar M, et al. 2010. Solute transport modelling in karst Conduits with slow zones during different hydrologic conditions[J]. Journal of Hydrology, 390(3): 182-189. |
Nordin C F, Troutman B M. 1980. Longitudinal dispersion in rivers:The persistence of skewness in observed data[J]. Water Resources Research, 16(1): 123-128. DOI:10.1029/WR016i001p00123 |
Raven K G, Novakowski K S, Lapcevic P A. 1988. Interpretation of field tracer tests of a single fracture using a transient solute storage model[J]. Water Resources Research, 24(12): 2019-2032. DOI:10.1029/WR024i012p02019 |
Rouse H. 1946. Elementary Mechanics of Fluids[M]. Dover, NY: Wiley, 376.
|
Runkel R L, Chapra S C. 1993. An efficient numerical solution of the transient storage equations for solute transport in small streams[J]. Water Resources Research, 29(1): 211-215. DOI:10.1029/92WR02217 |
Runkel R L.1998.One-dimensional transport with inflow and storage (OTIS): A solute transport model for streams and rivers[R].USGS, Water-Resources Investigations Report. 98-4018
|
Runkel R L. 2002. A new metric for determining the importance of transient storage[J]. Journal of the North American Benthological Society, 21(4): 529-543. DOI:10.2307/1468428 |
Thackston E L, Schnelle K B Jr. 1970. Predicting effects of dead zones on stream mixing[J]. Journal of the Sanitary Engineering Division, American Society of Civil Engineers, 96(SA2): 319-331. |
Toride N, Leij F J, Genuchten M T. 1993. A comprehensive set of analytical solutions for nonequilibrium solute transport with first-order decay and zero-order production[J]. Water Resources Research, 29(7): 2167-2182. DOI:10.1029/93WR00496 |
Toride N, Leij F J, Van Genuchten M T.1999.The CXTFIT code (Version 2.1) for estimating transport parameters from laboratory or filed tracer experiments[Z].US Salinity Laboratory, Agricultural Research Service, US Department of Agriculture, Riverside, California.
|
Valentine E M, Wood I R. 1977. Longitudinal dispersion with dead zones[J]. Journal of the Hydraulics Division, 103(HY9): 975-990. |
Valentine E M, Wood I R. 1979. Experiments in longitudinal dispersion with dead zones[J]. Journal of the Hydraulics Division, 105(HY8): 999-1016. |
Van Genuchten M T, Wierenga P J. 1976. Mass transfer studies in sorbing porous media I.Analytical solutions[J]. Soil Science Society of America Journal, 40(4): 473-480. DOI:10.2136/sssaj1976.03615995004000040011x |
Van Genuchten M T, Wierenga P J. 1977. Mass transfer studies in sorbing media, II, Experimental evaluations with tritium[J]. Soil Science Society of America Journal, 41(2): 272-278. DOI:10.2136/sssaj1977.03615995004100020022x |
Van Genuchten M T, Wagenet R J. 1989. Two-site/two-region models for pesticide transport and degradation:theoretical development and analytical solutions[J]. Soil Science Society of America Journal, 53(5): 1303-1310. DOI:10.2136/sssaj1989.03615995005300050001x |
White W B. 1988. Geomorphology and Hydrology of Karstic Terrains[M]. New York: Oxford University Press, 464.
|
Wörman A, Packman A I, Johansson H, et al. 2002. Effect of flow-induced exchange in hyporheic zones on longitudinal transport of solutes in streams and rivers[J]. Water Resources Research, 38(1): 2-1. |
Zaramella M, Marion A, Lewandowski J, et al. 2016. Assessment of transient storage exchange and advection-dispersion mechanisms from concentration signatures along breakthrough curves[J]. Journal of Hydrology, 538: 794-801. DOI:10.1016/j.jhydrol.2016.05.004 |
Zhao X E, Chang Y, Wu J C, et al. 2017. Laboratory investigation and simulation of breakthrough curves in karst conduits with pools[J]. Hydrogeology Journal, 25(8): 2235-2250. |
Zhao X E, Chang Y, Wu J C, et al. 2019. Effects of flow rate variation on solute transport in a karst conduit with a pool[J]. Environmental Earth Sciences, 78(7): 237. DOI:10.1007/s12665-019-8243-y |
 2020, Vol. 40
2020, Vol. 40


