2. 北京建筑大学, 北京未来城市设计高精尖中心/中荷未来污水技术研发中心, 北京 100044;
3. ASM Design B. V. /中-荷未来污水技术研发中心, 荷兰 3572 KX
2. Beijing University of Civil Engineering and Architecture, Beijing Advanced Innovation Center of Future Urban Design/Sino-Dutch R & D Centre for Future Wastewater Treatment Technologies, Beijing 100044;
3. ASM Design B. V. /Sino-Dutch R & D Centre for Future Wastewater Treatment Technologies, the Netherlands 3572 KX
污水厂生物建模技术作为集工艺设计、优化与研发为一体的超级辅助工具, 在国际上已广泛应用于各类市政污水处理厂的问题诊断与运行优化, 如利用TUD-ASM联合代谢模型实现对荷兰低负荷污水厂BCFS同步脱氮除磷工艺的模拟优化(Meijer et al., 2001);通过Biowin-ASDM模型完成对美国大型市政污水处理厂五段Bardenpho工艺曝气系统的优化与改造(Rieger et al., 2010);以及借助ASM2d模型对日本大型市政污水厂进行多级AO工艺模拟实现原位升级改造(Naoyuki et al., 2015).生物建模实践方法在国际上亦比较成熟, 分别以国际水协的IWA活性污泥建模导则(Rieger et al., 2012)及联合国水教育学院的IHE活性污泥建模指南(Meijer et al., 2012)为主.在国内, 通过翻译并引入IWA活性污泥建模导则, 污水厂生物建模技术正逐步从学术研究向工程领域探索(郝二成等, 2018;魏忠庆等, 2019).但在模型应用方面, 国内仍缺乏对模拟结果的实践与验证, 亦无法进一步总结与优化符合中国国情的系统建模方法.
当前, 随着国内日益收紧的高排放标准和污水厂愈发迫切的节能降耗(能耗、药耗)需求, 为污水厂建立可靠性高的具有工艺诊断和风险预测等功能的生物模型已成为必要手段.然而, 数据质量是影响模型可靠性的关键因素(Meijer et al., 2002;Puig et al., 2008).因此, 在IWA及IHE国际标准建模导则中均强调了建模数据收集、数据清洗的重要性.在国内实践中, 污水处理厂在常规运行指标的测量、存储、统计等方面尚不完善, 导致大量与生物建模相关的水质数据缺失且历史数据普遍存在大误差.所以, 对国内污水处理厂进行生物建模, 首先要根据实际情况优化数据收集的要求与方法, 既要保证数据信息的真实性与必要性, 又要考虑数据收集的可执行性.然而, 真实的数据并非一定是有效的.系统误差、偶然误差无论在实验室、在线仪表、传感器信号传输等过程中均会产生.为了获取能够正确描述污水厂运行状态的有效数据, 还需进一步结合数据清洗方法以识别可疑数据、剔除大误差并闭合物料平衡关系、恢复数据间的逻辑性与一致性.
在数据清洗方面, 国内已有研究提出了相关改善数据质量的方法, 如物料平衡计算法(郝晓地等, 2009)并成功应用于实验室小试建模.但该方法依赖于可靠的水质测量数据, 仅通过修正系统流量闭合物料平衡, 尚无法评估该方法针对国内污水处理厂水质数据可靠性较差时的适用性.在此方面, 国外部分研究提出了数理统计分析法辅助剔除测量大误差, 如拉格朗日乘数法(Lee et al., 2015), 相对标准偏差法(Meijer et al., 2015)等.但该方法需基于当地水质特点建立相关特征值, 再结合数理统计学方法进行辅助判断与分析, 在缺乏相关参考阈值与判断标准的情况下, 尚无法在国内直接应用.有鉴于此, 本文立足于国内污水厂的数据问题对国际标准生物建模方法进行创新, 并通过实际案例应用, 进一步研究数据清洗对污水处理厂生物建模可靠性影响.
2 材料和方法(Materials and methods) 2.1 技术路线数据清洗对污水处理厂生物建模可靠性影响研究技术路线绘制于图 1.首先, 分析并指出国内污水厂实现精准建模的瓶颈与问题, 结合国外研究方法与国内现实情况对建模方法进行创新, 并对3步数据清洗方法实施步骤进行详细阐述.然后, 将该方法应用于实际污水厂建模, 验证方法的可行性.最后通过对比模型的拟合结果、校正参数数量及合理性, 评估数据清洗对污水处理厂生物建模的可靠性影响.
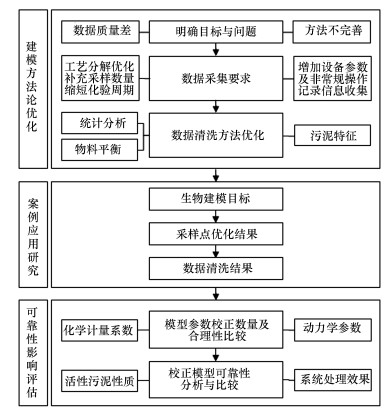 |
| 图 1 数据清洗对污水处理厂生物建模可靠性影响研究技术路线图 Fig. 1 Technical route for effect of data cleaning on reliability of biologically modeling WWTPs |
由于国内目前尚无系统性的建模方法, 因此, 基于IWA生物建模导则, 将国内在实践中逐步形成的建模流程与IHE国际生物建模指南进行比较.如图 2所示, 国际建模方法十分强调原始数据的可靠性, 并通过物料平衡计算及模型校正反复对原始数据进行清洗与验证.在其完整建模周期中, 约70%~80%的时间用于前期数据处理, 目的是降低错误数据对让模型校正的影响.相反, 国内建模的重心则主要基于模型进行情景模拟与比较.
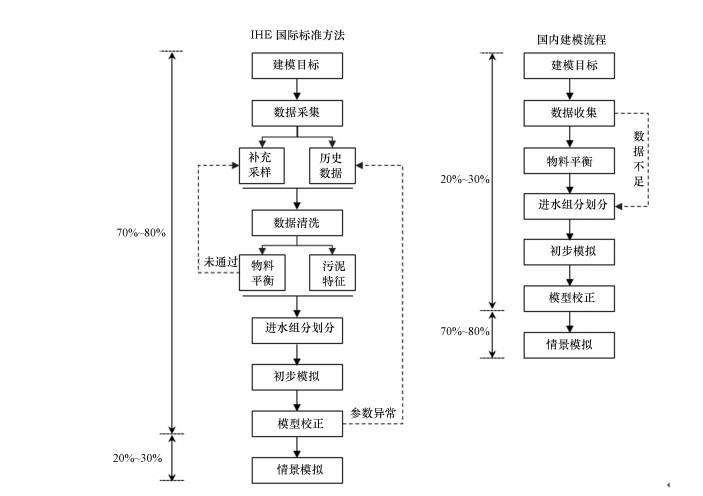 |
| 图 2 国内外污水处理厂建模方法流程图 Fig. 2 Flow diagrams of domestic and international modeling WWTPs methods |
显然, 通过对基础数据的详细收集与清洗, 修正后的数据更能够反映水厂的真实运行状态, 校正后的生物模型亦能实现对污水厂的量化比较与分析, 但弊端在于建模周期偏长, 且对原始数据质量、数量要求较高.国内经验建模流程虽避开了繁琐的数据清洗与验证过程, 极大缩短了建模周期, 但校正后模型的可靠性难以准确评估, 只能通过横向模拟计算实现对污水厂的定性分析.事实上, 受限于国内缺乏系统性的生物建模方法, 且数据清洗方法亦缺少明确规定与判断标准, 导致模型可靠性难以进一步提高.因此, 立足于国内污水厂实际情况, 将IHE国际标准建模方法实现本土化创新具有现实意义.
2.3 基于数据清洗的本土化生物建模方法基于数据清洗的本土化建模方法如图 3所示, 在IHE国际标准建模方法的基础上, 本研究针对国内水厂实际情况提出的建模方法主要有以下4点改进:
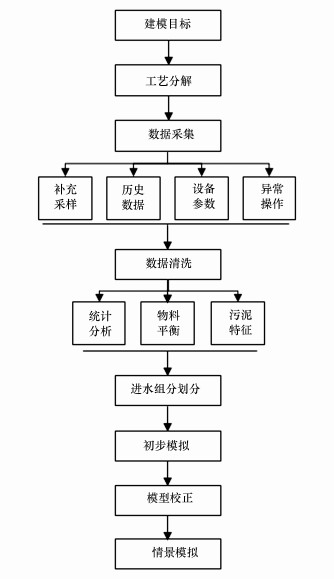 |
| 图 3 基于数据清洗的本土化建模方法流程图 Fig. 3 Flow diagram of localized modeling method based on data cleaning |
① 明确建模目标是一切污水厂生物建模工作的关键出发点(Meijer et al., 2015), 本方法中主要用于快速聚焦关键问题、简化实际情况, 确定建模过程对基础数据在时间及空间尺度的需求.
② 针对国内水厂普遍缺失建模水质数据导致补充采样与化验任务量过大的问题, 提出在开展数据采集工作前, 采用工艺分解法优化采样点设计——在准确描述工艺流程前提下, 根据各构筑物功能并结合流量计位点进行子系统划分, 划分的区域同时将作为物料平衡校核的计算边界.对工艺流程进行分解可以按需定位数据采集位点, 避免非必需的数据样本数量, 有效缩短化验时间.
③ 除必需的补充采样数据外, 需同步收集一定时间内(如1年)历史运行数据、设备参数及中控室/运行班组的非常规操作内容与时间节点, 具体包括:水厂实验室化验数据、在线仪表水质/流量监测数据、脱水污泥外运量数据、泵机组运行数量与额定流量, 操作运行日志等.通过以上数据综合了解水厂运行状态, 辅助数据清洗对异常值的判定和剔除.
④ 在国外数据清洗方法研究基础上, 提出可行性数据处理步骤及参考阈值判断标准.基本步骤为:首先通过统计分析法筛选可疑数据并标定异常值, 然后利用物料平衡计算法剔除大误差, 使实测数据集通过物料平衡校核, 最后根据污泥特征分析法进一步修正污泥组分.下面对数据清洗的核心方法进行详细阐述.
2.4 统计分析法利用数理统计学方法分析样本数据常见于各类数据分析研究中, 常见方法有计算平均值、标准差、相关系数、回归分析等判断数据间相互联系的规律性(Wan et al., 2017;Zhang et al., 2018).在前期收集的大量基础数据中, 用于建模的进水、出水水质数据首先需要统计一段时间内的样本均值, 该值是模型稳态校正的关键信息.然而, 收集的水质数据在统计区间内通常是不断变化的, 一方面来源于水质本身的正常波动, 另一方面则来自于测量误差.统计学研究表明, 当统计区间内样本数量较少时, 偶然误差对样本均值影响的敏感性远高于数据的真实波动(Kolodyazhnyi et al., 2009).因此, 对于国内污水厂建模而言, 当模型校正依赖于样本数量有限的补充采样数据时, 测量误差是影响数据可靠性的主要原因.
在污水处理过程中, 当污水厂接纳的排污区域无明显变化时, 系统进水水质通常呈现一定规律的波动;当生物处理段运行方式无明显改变时, 系统出水经过生物段的缓冲, 波动幅度显著低于进水.利用污水处理的这一特征, 在荷兰相关建模案例研究中(Meijer et al., 2015), 结合荷兰污水水质特征, 利用相对标准偏差(RSD)≤15%作为判断水质数据波动情况是否正常的依据, 其基本计算公式为:
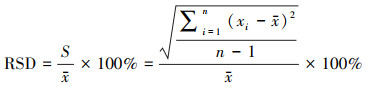
|
(1) |
式中, S为标准偏差, x为样本平均值.
在国内实践中, 由于工业水偷排、雨污管网混接等现象导致污水厂进水水质易出现较大幅度波动.结合国内不同水厂进水水质情况所得到的RSD经验阈值≈20%.因此, 本研究推荐当RSD≤20%时, 数据集出现测量误差的可能性低, 即数据可靠度较高;当RSD>20%时, 则认为该组数据存在测量误差可能性高, 数据可疑.
2.5 物料平衡计算法利用物料平衡原理修正原始数据的计算方法被广泛应用于化工生产领域已逾数十载(Madron et al., 1992;van der Heijden et al., 1994), 这一方法直至近些年才慢慢在污水处理工程领域引起重视, 并率先在荷兰、法国等欧洲国家和地区的污水处理厂工艺诊断、仪表优化设计等层面开展研究与应用(Puig, 2008;Villez et al., 2016;Behnami, 2016).在国内, 将物料平衡理论用于原始数据的可靠性评价亦有深入研究, 并成功应用于实验室小试数据分析(郝晓地等, 2009), 该研究认为对任何污水处理厂, 宏观上系统的进/出口间物质都满足式(2)的物料平衡关系:
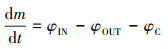
|
(2) |
式中, 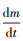
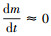
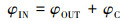
|
(3) |
当一个满足式(3)平衡中的未知量可全部通过测量获得时, 称为封闭平衡, 否则该平衡称为开放平衡.在活性污泥系统中, 只有流量平衡(忽略蒸发量)、TP平衡和TSS平衡理论上属于封闭平衡;而其他平衡如COD、TKN、TN、NH4+、NO3-平衡因涉及到CO2、N2O、N2、NH3等气体的产生与溢散, 气态部分无法直接测量, 因此属于开放平衡.在实际应用中, 只有封闭平衡可用于物料平衡校核, 开放平衡的建立与否则取决于建模目标对基础数据的需求.借助已有闭合平衡中的流量关系可计算出无法直接测量的部分, 进而闭合开放平衡.理想情况下, 封闭平衡与开放平衡关系均成立, 式(3)可表示为:
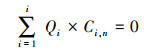
|
(4) |
实际情况下, 测量误差导致实际平衡关系通常存在一个残差εn, 即:
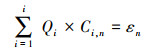
|
(5) |
式中, εn越大表明系统的测量误差越大, 数据可靠性越低.
为了降低残差εn、闭合物料平衡关系还需确定物料平衡计算边界, 每个划分区域可根据式(4)相应列出多个闭合平衡与开放平衡关系.理论上, 子系统越多、平衡关系越多, 表明更多的未知量能够通过平衡关系计算得出, 部分可靠性较低的数据亦可通过其他可靠性较高数据通过平衡关系计算得到理论平衡值, 从而得到修正.然而, 对于大多数污水处理厂而言, 常规历史数据难以满足建立物料平衡的需求, 需要进行额外的补充采样才能保证建立足够的物料平衡.在这种情况下, 确定合理的物料平衡计算边界, 在满足建立物料平衡关系前提下减少额外补充样本的数据量是该方法实践中的核心问题.
有鉴于此, Le等(2018)利用帕累托最优解法提出一种采样方案的优化设计方法, 在满足污水处理厂物料平衡需求前提下, 寻求成本与数据精度之间的最佳平衡点.基于同样的思考, 本研究提出的简化方法为:
① 定位工艺流程中具有流量记录的数据位点, 结合各构筑物功能进行子系统(物料平衡计算边界)初步划分.
② 利用合并、叠加等方式精简子系统数量, 且需保证不同子系统之间至少共享1个物质流通量或至少存在1个相同的参数变量.
③ 子系统的物料平衡关系全部围绕封闭平衡搭建, 并至少保证1组平衡关系中的所有变量需要全部测量(已知).
④ 对残差相对较大的平衡, 结合数据相对标准偏差(RSD)分析结果, 优先剔除浓度测量数据中可疑的大误差数据, 再对敏感性更高的流量数据进行合理修正, 使平衡闭合.
2.6 污泥特征分析法基于封闭平衡的物料校核仅能完成对流量、TSS、TP 3个指标数据的校核, 对开放平衡中的相关数据本研究采用污泥特征分析法.因为在正确描述工艺的基础上, 活性污泥模型具有模拟和预测功能的前提是能够准确模拟实际活性污泥系统的污泥特征与性质.对水厂的长期监测发现, 当工艺调整不频繁的情况下, 系统中活性污泥的组分通常在一段时间(一个污泥龄周期)内比较稳定, 活性污泥中各物质含量的比例接近于定值(如活性污泥中CODX: TKNX: TPX: VSS ≈定值).根据这一污泥特征, 荷兰IHE模型导则中推荐利用曝气池中污泥组分信息对模型进行校正, 并提供部分污泥组分推荐参考值, 如:CODX/VSS≈1.32~1.42, TKNX /CODX≈0.05~0.08, TPX /CODX≈0.035~0.055(Meijer et al., 2012).
然而, 该方法并不能直接应用于国内污水厂建模:一方面, 由于国内长期对污泥指标的忽视, 导致难以直接获得污泥特征的有效数据信息;另一方面, 受限于污水厂本地检测条件和检测方法, 当水厂投加大量Fe/Al盐所产生的化学污泥与生物污泥发生混合时, 常规水质检测手段难以有效检出混合污泥中的无机磷含量, 导致污泥TP数据出现系统误差可靠性差.有鉴于此, 本研究采用欧洲标准测试测量组织的SMT法测TP(Ruban et al., 1999), 该方法已广泛用于活性污泥测量(刘艳芳等, 2019;王超等, 2019), 具体方法为:
① 采用国标法完成对曝气池混合水样及脱水污泥样品TCOD、SCOD、TKN、NH4、PO4、TSS、VSS的检测.采用SMT法, 完成对曝气池混合水样及脱水污泥样品TP的检测.
② 分别计算曝气池污泥与脱水污泥各组分比例关系:VSS/TSS、CODX/VSS、TKNX /CODX、TPX /CODX, 其中CODX=TCOD-SCOD, TKNX =TKN-NH4, TPX =TP-PO4.
③ 根据国际推荐参考值与各污泥组分实际计算值, 初步修正污泥组分比值.再利用物料平衡闭合后的污泥TP、TSS浓度, 及修正后的污泥组分比值, 反算TCOD、TKN、VSS值.利用反算浓度值剔除原始数据大误差, 迭代确定污泥组分.
2.7 研究对象本研究对象为天津宁河芦台桥北污水处理厂, 数据源为该厂2019年1—7月实验室常规水质化验报表、SCADA系统在线流量数据表及2019年8月12日、14日、22日补充采样化验数据.所有数据均基于Microsoft Power BI软件进行整理、分析与可视化输出.污水厂生物建模软件采用EnviroSim Biowin 5.3, 活性污泥模型为软件内嵌的活性污泥-厌氧消化联合代谢模型(ASDM模型), 该模型以国际水协ASM模型为核心, 已被广泛应用于国内外污水处理厂生物建模研究(Elawwad et al., 2019).
案例厂位于天津市宁河区贸易开发区小崔路(39.33°E, 117.79°N), 设计处理规模12000 t·d-1, 实际处理量约8000 t·d-1.2019年实验室数据显示, 日平均进水水质为:CODCr为99 mg·L-1, BOD5浓度为36 mg·L-1, SS浓度为93 mg·L-1, TN浓度为28 mg·L-1, NH4+-N浓度为21 mg·L-1, TP浓度为3.2 mg·L-1.出水需满足天津市《城镇污水处理厂水污染物排放标准》(DB12599—2015)A标准:COD≤30;BOD ≤6;NH4≤1.5 (3);TN≤10;TP ≤0.3.该厂主体采用AAO +反硝化滤池工艺, 分别在厌氧池前端与反硝化滤池前端投加大量复合型碳源以保证出水TN达标;在曝气池末端投加过量FeCl3盐以换取出水TP稳定达标.因此, 本研究的建模目标为准确模拟该厂碳源实际投加量, 并提出合理的碳源优化方案.根据建模目标及水厂历史数据情况可首先确定建模基础数据需求, 再根据本土化建模方法完成对案例厂的生物建模.
3 结果与讨论(Results and discussion) 3.1 采样点优化结果鉴于该厂历史水质数据中缺少必要的建模水质信息, 导致补充采样量大、化验周期长.因此, 首先通过工艺分解对采样点进行优化设计.模拟研究主要基于工艺的核心生化反应段, 对预处理及三级处理进行合理简化后, 使各采样点分布于核心工艺段.考虑到物料平衡计算方法对水质与水量要求, 根据SCADA系统记录确定9处已知的流量数据位点和2处可估算出的流量数据点, 并以此进行子系统划分.划分后的子系统区域及采样点见图 4.
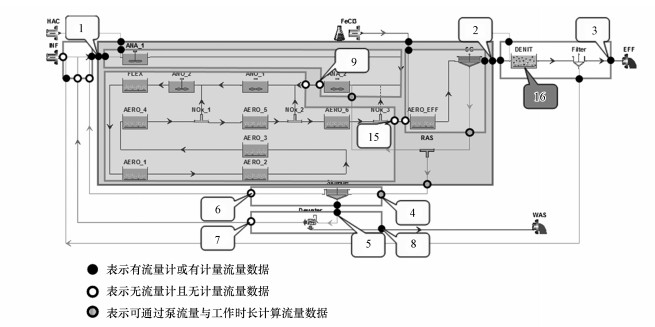 |
| 图 4 Biowin工艺流程示意图及工艺流程分解 Fig. 4 Diagram of technological process in Biowin and process decomposition |
此外, 为便于分析工艺同步脱氮除磷效率、辅助模型校正, 对该厂额外增加生化池沿程采样点(编号10~14), 详细采样方案与水质化验项目见表 1.通过工艺分解对采样点进行优化, 可有效预知基于物料平衡校核进行数据清洗时所需最小数据量, 减少补充样本数量并确定数据采集位点.优化后, 每日采集样本数量为41个, 并可于一周内完成3组共计459个补充数据的检测.
| 表 1 补充水样采集方案与化验项目 Table 1 Collection scheme and test items of supplementary water sample |
首先通过统计分析方法标定可疑数据, 并发现补充采样期内3日进水数据整体RSD值偏高, 表明补充检测进水数据可靠性较低.通过24 h进水日变化曲线分析发现, 虽然历史进水数据均为每日9点的瞬时水样, 但其数值上较接近日平均进水水质, 如图 5所示.因此, 考虑将历史进水数据代入物料平衡计算公式, 出水水质、污泥浓度则采用剔除明显异常值后的补充采样结果, 初始流量数据为SCADA历史在线数据.根据图 4中划分的9组子系统作为物料平衡计算边界, 包括流量、TP、TSS平衡在内共计21个平衡方程, 代入原始流量计算得到平衡闭合前的残差列于表 2.
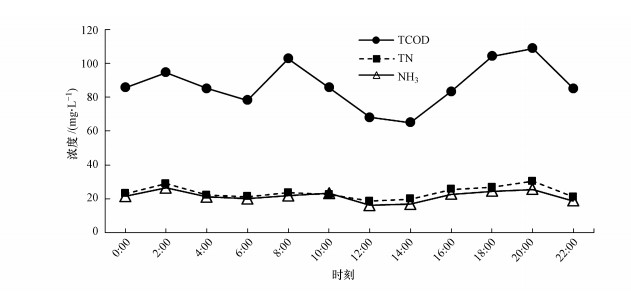 |
| 图 5 宁河污水厂24 h进水日变化曲线 Fig. 5 Diagram of 24 h-influent variation of WWTP Ninghe |
| 表 2 原始物料平衡计算表 Table 2 Calculation table of non-closed mass balance |
根据本研究提出的可行性方法, 合理调整流量数据对21个封闭平衡进行闭合, 物料平衡校核结果列于表 3.经过物料平衡修正后的水量数据输入Biowin模型可以最大程度减少流量导致的系统误差, 剔除大误差后的TP及TSS水质数据可用于准确计算和分析污泥龄.在模型校正阶段, 由于模型中各物质之间遵循绝对的物料平衡关系, 因此只有向模型中输入已经闭合的数据集, 才能够通过参数的调整实现模型值与实测值的吻合, 否则无法完成模型校正.
| 表 3 物料平衡校核结果 Table 3 Results of mass balance calculation |
根据污泥特征分析方法, 分别获得曝气池混合水样和脱水污泥样品的测量结果.由于案例厂通常在污泥脱水时加入PAM以辅助污泥絮凝提高脱水效果, 因此, 首先通过理论计算排除了投加PAM对脱水污泥组分可能造成的系统误差, 进一步结合实际测量值及闭合后的数据集分别计算出曝气池与脱水污泥中的4组典型污泥组分比值.最终污泥组分修正结果见表 4, 可以发现案例厂污泥组分与国外给出的参考值存在个别差异:①VSS/TSS比例明显偏低表明在生化池中的有效生物量较低, 该现象与向生化池中投加大量除磷药剂以及进水中的无机颗粒ISS有关;②CODX/VSS曝气池与脱水污泥实测比例有较大差异, 修正值低于国外参考值, 表明单位质量污泥具有较低的有机质含量.
| 表 4 污泥组分修正结果 Table 4 Results of sludge component correction |
为便于比较数据清洗对模型参数校正上的影响, 本案例首先采用上节清洗后的数据对模型进行校正, 再将原始数据直接代入模型尝试进行拟合, 最后对两种方法的校正参数进行比较.
利用清洗后的数据进行模型校正时, 参考Meijer提出的校正方法(Meijer et al., 2012).模型参数中, 对模拟结果影响敏感性较高的参数为动力学参数和化学计量系数.其中, 动力学参数主要影响反应过程的快慢, 该参数受环境、水质、运行工况等多种因素的综合影响, 不同污水厂之间通常具有较大差异, 且动力学参数往往难以通过实验准确测量;而化学计量系数主要表征反应物质间的质量比, 在固定的生化反应过程中, 消耗物质与生成物质间的质量比通常是比较稳定的.因此, 在模型校正过程中, 优先通过调整动力学参数实现模拟数值拟合, 仅当具有可靠实测结果时才调整化学计量系数(如活性污泥组分).除进水组分基础划分参数外, 本次共校正11个核心参数.校正后的模型参数及参数校正原因列于表 5, 包括1个进水组分参数(FUP)、1个化学计量系数(INOHO)、5个动力学参数(YAOB、KNH4、KHO2、KAO2、KNO2)、2个计量转换系数(XI : VSS、XS : VSS)、1个氧传质参数(αF)、1个化学平衡参数(KPFe).其中, FUP、KNH4为调整幅度较大的两个参数, 前者表明进水COD惰性组分较高, 后者表明系统硝化性能较差.由于此时基于正确的工艺描述及经过清洗后的数据进行建模与校正, 因此该组参数可用来表征该厂活性污泥系统的主要问题与运行优化瓶颈.
| 表 5 基于清洗数据模型校正参数表 Table 5 Table of model calibration parameters based on data cleaning |
利用原始数据进行模型校正时, 因原始数据不满足最基本的物料平衡关系, 因此, 校正方法采用对出水结果的强制拟合.最终共修改18个核心参数, 拟合后的模型参数表列于表 6, 包括1个进水组分参数(FUP), 5个化学计量系数(INOHO、INXI、INNOB、IPXI、IPOHO)、9个动力学参数(YAOB、YNOB、YOHO、KNH4、KHO2、KAO2、KNO2、KNNO2、KOHO)、2个计量转换系数(XI : VSS、XS : VSS)、1个氧传质参数(αF)、1个化学平衡参数(KPFe).事实上, 为获得更好的出水拟合效果, 大量参数均可进行修改.在尽可能减少模型参数修改的原则上, 表 6修改的模型参数数量仍多于表 5.比较两组结果可以发现, 为了强制拟合出水N、P浓度, 导致额外的4个化学计量系数和4个动力学参数被修改.其中, INOHO、INXI、INNOB的修正幅度已远超理论值, 表明提供的原始数据中有极大可能性存在大误差.
| 表 6 基于原始数据模型拟合参数表 Table 6 Table of model fitting parameters based on original data |
同样, 为便于分析比较基于清洗数据与原始数据校正/拟合后模型的可靠性.首先代入表 5中的校正参数, 将历史平均进水水质及当前运行工况输入模型;再重新代入表 6中的拟合参数, 输入相同进水水质及运行工况.最后分别对两种情况得到的出水、曝气池、脱水污泥的稳态模拟结果与实测结果进行比较, 并计算比较生化段主要污染物指标去除率, 计算结果列于表 7.模拟结果对比表明, 利用清洗数据校正的模型可很好的反映实际水厂的污泥性质与处理效果, 该模型在仅校正11个核心参数情况下, 对核心生化段主要污染物去除率的模拟误差≤3%.而利用原始数据校正的模型, 虽各项出水指标拟合效果良好, 但对曝气池及脱水泥的拟合偏差非常高, 核心生化段主要污染物去除率的模拟误差亦高于前者.表明校正模型虽拟合了出水结果, 但并不能准确反映实际污水厂的污泥性质和处理能力.
| 表 7 模拟结果对比 Table 7 Comparison of simulation results |
在模型验证方面, 由于该厂在运行期间对曝气量、处理线水量分配、排泥量等关键运行参数调整频繁且无详细运行记录, 导致难以在校正后的模型中重现历史运行工况;另一方面, 历史运行数据中仅有原始进、出水水质数据, 缺少重要的生物池过程指标及污泥组分数据, 导致难以对补充测样期以外的其他数据集进行有效的数据清洗, 特别是无法闭合物料平衡关系.在这种情况下, 校正后的模型难以进行针对不同数据集的验证.本案例中, 基于数据清洗建立的生物模型基于历史平均进水水质及当前运行工况进行校正, 并实现了对活性污泥性质及污染物去除效果的精确拟合, 表明调整的模型参数能够正确描述该厂目前活性污泥系统的特征与问题.因此, 本研究基于清洗数据校正后的模型已具有精准分析并指导该污水处理厂运行优化的功能, 亦可完成多种情景、不同尺度的模拟预测分析.
4 结论(Conclusions)1) 结合国内污水处理厂实际问题与建模需求, 在IHE生物建模指南基础上创新, 提出一种基于数据清洗的本土化污水厂生物建模方法, 并通过实际建模案例研究验证了该方法的有效性.利用这一方法能对国内污水厂原始数据进行有效检查与评估, 实现精确生物建模.
2) 数据清洗过程虽增加了额外的数据采集与处理量, 但能够显著提升基础建模数据质量、简化模型校正过程并大幅提高生物模型可靠性.
3) 生物模型可靠性依赖于原始数据质量, 而非对模型参数的大量调整以实现强制拟合.校正模型应能够准确描述活性污泥系统的特征与问题, 才能在工艺优化、风险预测时发挥可靠作用.
Behnami A, Shakerkhatibi M, Dehghanzadeh R. 2016. The implementation of data reconciliation for evaluating a full-scale petrochemical wastewater treatment plant[J]. Environmental Science and Pollution Research international, 23(22): 22586-22595. DOI:10.1007/s11356-016-7484-5 |
Elawwad A, Matta M, Abo-Zaid M, et al. 2019. Plant-wide modeling and optimization of a large-scale WWTP using BioWin's ASDM model[J]. Journal of Water Process Engineering, 31: 100-108. |
郝晓地, 胡沅胜, 王克巍. 2009. 污水处理厂原始数据可靠性评价方法[J]. 环境科学学报, 29(10): 2081-2085. |
郝二成, 王如意, 胡志荣, 等. 2018. 大型污水处理厂工艺模拟应用实例[J]. 中国给水排水, 34(5): 82-87. |
Karr A F. 2006. Exploratory data mining and data cleaning[J]. Journal of the American Statistical Association, 101(473): 399. |
Kolodyazhnyi A N, Postnikov E V. 2009. Estimating the errors of measurement time correlations[J]. Measurement Techniques, 52(4): 344-348. DOI:10.1007/s11018-009-9290-7 |
Lee S, Rao S, Kim M J, et al. 2015. Assessment of environmental data quality and its effect on modelling error of full-scale plants with a closed-loop mass balancing[J]. Environment Technology, 36: 3253-3261. DOI:10.1080/09593330.2015.1058859 |
Le Q H, Verheijen P J T, van Loosdrecht M C M. 2018. Experimental design for evaluating WWTP data by linear mass balances[J]. Water Research, 142(31): 415-423. |
刘艳芳, 王凌霄, 马骏, 等. 2019. 剩余污泥臭氧化过程中磷的释放及形态转化[J]. 环境科学学报, 39(9): 3039-3044. |
Madron F, Veverka V. 1992. Optimal selection of measuring points in complex plants by linear models[J]. American Institute of Chemical Engineers, 38(2): 227-236. DOI:10.1002/aic.690380208 |
Meijer S C F, van Loosdrecht M C M, Heijnen J J. 2001. Metabolic modelling of full-scale biological nitrogen and phosphorus removing wwtp's[J]. Water Research, 35(11): 2711-2723. DOI:10.1016/S0043-1354(00)00567-4 |
Meijer S C F, van der Spoel H, Susanti S, et al. 2002. Error diagnostics and data reconciliation for activated sludge modelling using mass balance[J]. Water Science and Technology, 45: 145-156. |
Meijer S C F, Brdjanovic D. 2012. A Practical Guide to Activated Sludge Modelling[M]. UNESCO-IHE. 197-210
|
Meijer S C F, van Kempen R N A, Appeldoorn K J, et al. 2015. Applications of Activited Sludge Models[M]. IWA Publishing. 357-410
|
Naoyuki F, Shoichiro Y, Yoshio K, et al. 2015. Simulation of the operational conditions of the full-scale municipal wastewater treatment plant to improve the performance of nutrient removal[J]. Water Science & Technology, 36(12): 9-18. |
Puig S, van Loosdrecht M C M, Colprim J, et al. 2008. Data evaluation of full-scale wastewater treatment plants by mass balance[J]. Water Research, 42: 4645-4655. DOI:10.1016/j.watres.2008.08.009 |
Rahm E, Do H H. 2000. Data Cleaning:Problems and Current Approaches[J]. IEEE Data Engineering Bulletin, 23(4): 2000. |
Rieger L, Gillot S, Langergraber G, et al. 2012. Guidelines for Using Activaed Sludge Models[M]. IWA Publishing. 57-98
|
Reiger L, Takacs I, Villez K, et al. 2010. Data reconciliation for wastewater treatment plant simulation studies planning for high-quality data and typical sources of errors[J]. Water Environmental Research, 82: 426-433. DOI:10.2175/106143009X12529484815511 |
Ruban V, Brigault S, Demare D. 1999. An investigation of the origin and mobility of phosphorus in freshwater sediments from Bort-Les-Orgues Reservoir, France[J]. Journal of Environmental Monitoring, 1(4): 403-407. DOI:10.1039/a902269d |
van der Heijden R T, Heijnen J J, Hellinga C. 1994. Linear constraint relations in biochemical reaction systems:Ⅰ. Classification of the calculability and the balanceability of conversion rates[J]. Biotechnology and Bioengineering, 43(1): 3-10. DOI:10.1002/bit.260430103 |
Villez K, Vanrolleghem P A, Corominas L. 2016. Optimal flow sensor placement on wastewater trearment plants[J]. Water Research, 101: 75-83. DOI:10.1016/j.watres.2016.05.068 |
Wan H P, Todd M D, Ren W X. 2017. Statistical framework for sensitivity analysis of structural dynamic characteristics[J]. Journal of Engineering Mechanics, 143(9): 401-416. |
王超, 刘清伟, 职音, 等. 2019. 中国市政污泥中磷的含量与形态分布[J]. 环境科学, 40(4): 1922-1930. |
魏忠庆, 胡志荣, 上官海东, 等. 2019. 基于数学模拟的污水处理厂设计:方法与案例[J]. 中国给水排水, 35(10): 21-26. |
Zhang C H, Chen N. 2018. Statistical analysis of simulation output from parallel computing[J]. ACM Transactions on Modeling and Computer Simulation, 28(3): 1-22. |
 2020, Vol. 40
2020, Vol. 40


