随着中国经济的快速发展, 空气质量问题日渐突出, 细颗粒物PM2.5(空气动力学当量直径≤2.5 μm的颗粒物(Christopher et al., 2020))已成为我国大多数城市的首要污染物(周亮等, 2017).PM2.5与人体健康之间关系密切(郭新彪等, 2013), 其会加剧呼吸系统疾病和心血管疾病.世界卫生组织报告显示, 全球超过80%的人口正在面临空气污染问题(Maji et al., 2018).因此, 准确预测PM2.5浓度对大气污染防治和经济可持续发展具有重要的现实意义.
自2013年以来, PM2.5小时质量浓度数据通过中国国家环境监测中心(CNEMC)网站公开发布(Li et al., 2017).截至2019年底, 全国已经建立了约1600个地面站点, 用来监测中国的总体空气质量.但由于地面监测站点空间分布不均匀(赵滨等, 2020), 利用地面监测站大面积监测中国区域PM2.5浓度仍存在很大困难.基于卫星的遥感监测可以快速获取大范围的空间数据集, 因此, 利用卫星遥感监测近地面PM2.5浓度逐渐成为研究热点(徐建辉等, 2015; 吴健生等, 2017; 于雪等, 2017; 陈优芳等, 2019).已有研究表明, 卫星监测的气溶胶光学厚度(AOD)与PM2.5浓度之间有很强的相关性(陶金花等, 2013; 李同文等, 2015).夏志业等(2015)利用MODIS AOD产品反演了北京近地面PM2.5浓度, 经过标高订正和湿度订正后, 两者的相关系数为0.467, 验证了利用MODIS AOD监测PM2.5污染的可行性.考虑到PM2.5浓度受多种因素的影响, 一些研究人员将气象因子纳入了回归模型.例如, Benas等(2013)利用相对湿度、温度、风速等因子构建了多元线性回归模型, 提升了PM2.5浓度的反演精度.田宏伟等(2020)利用AOD、地面气象观测能见度和相对湿度数据, 对比了半经验模型和非线性多元回归模型, 结果表明, 非线性多元回归模型优于半经验模型.考虑到PM2.5与AOD等因子的空间异质性, 一些学者引入了地理加权回归(GWR)模型(邵彦川等, 2018; 陈辉等, 2019; 付宏臣等, 2020), 获得了比统计回归模型更好的结果.但GWR模型通常只能表述局部空间数据非平稳的问题, 不能准确地刻画中国区域PM2.5浓度空间分布.
随着研究的深入, PM2.5浓度估算逐渐被认为是一种复杂的多变量非线性问题.考虑到机器学习能够很好地刻画PM2.5浓度与预测因子之间的复杂非线性问题, 许多研究人员将机器学习方法用于PM2.5浓度估算(Chen et al., 2018;Pan et al., 2018;邵琦等, 2018; Dong et al., 2020; Shao et al., 2020;Yuan et al., 2020).例如, 刘林钰等(2020)利用深度学习神经网络(DNN)在华东地区开展实验, 发现DNN反演的PM2.5精度高于传统的线性和非线性模型.夏晓圣等(2020)利用随机森林模型(RF)研究了中国区域PM2.5浓度空间分布的影响因素及其区域差异, 结果表明, RF模型估算的PM2.5浓度精度高于多元线性回归和BP神经网络(BPNN).康俊锋等(2020)以江西省赣州市为例, 对比了XGBoost、RF、BPNN、GPR、SVR、KNN 6种机器学习模型, 结果表明, XGBoost模型的估算精度高于其他5种机器学习模型, 但该研究没有考虑站点数据时空相关性, 导致PM2.5浓度估算精度不高.考虑到PM2.5浓度估算过程中地面监测站点数据时空相关性问题, 有些学者将PM2.5监测站点数据进行反距离加权(IDW)插值结果作为机器学习模型的输入数据(Li et al., 2017; Wei et al., 2019; Chen et al., 2020), 以提高模型预测结果.然而, IDW忽略了站点数据间的空间结构信息, 导致预测结果精度不高.相较于IDW插值, 克里金(Kriging)插值通过计算站点变异函数, 充分考虑了站点数据的空间结构信息, 是一种无偏最优插值方法, 可实现空间信息的准确估计.
基于此, 本文将Kriging方法引入到PM2.5估计中, 并以精度较高的XGBoost算法为基础, 构建一种时空XGboost(Space-time XGboost, STXGB)模型.该模型的优势在于将Kriging方法获取的时空自相关因子作为输入变量, 通过变异函数充分考虑了站点数据的空间相关性, 进而提高了PM2.5浓度的空间估算精度.同时以2019年中国区域月数据为例, 验证STXGB模型的精度和可靠性.
2 研究区域和数据源(Study region and data) 2.1 研究区域本文选取中国为研究区域(北纬3°~54°, 东经73°~136°).截至2019年底, 全国建立了约1600个PM2.5地面监测站点, 空间分布见图 1.结果表明, PM2.5地面监测站点分布不均匀, 整体呈现出东部多、西部少, 城市地区多、偏远农村地区少的特点.
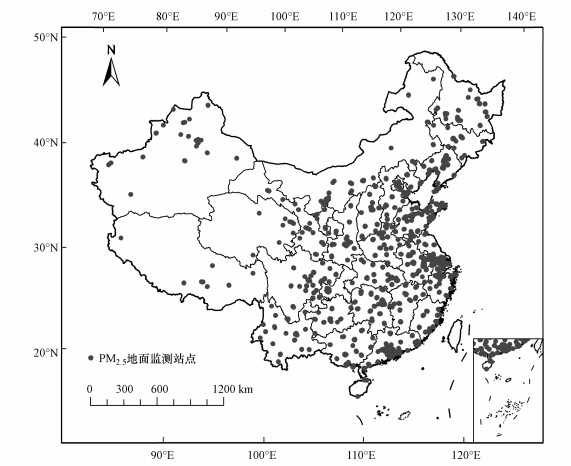 |
| 图 1 中国区域PM2.5地面监测站点分布 Fig. 1 Distribution of PM2.5 ground monitoring stations in China |
① PM2.5监测站点数据:2019年1—12月的日均PM2.5质量浓度数据来自中国国家环境监测中心(CNEMC)网站(http://www.cnemc.cn).PM2.5浓度采用锥形元件振荡微量天平或β衰减法测量, 校准和质量控制符合国家标准GB3095—2012(杜震洪等, 2020).
② 气溶胶光学厚度(AOD)数据:AOD数据来自LAADS网站(http://ladsweb.nascom.nasa.gov).Terra和Aqua卫星上搭载的中等分辨率成像光谱仪(MODIS)提供了多种分辨率的气溶胶产品(杨立娟等, 2018), 本文研究采用的是Terra卫星的MOD04_3K产品数据和Aqua卫星的MYD04_3K产品数据, 时间分辨率为天, 空间分辨率为3 km×3 km.
③ 气象数据:本研究使用的气象数据来自欧洲中期天气预报中心(ECMWF), 使用的是EAR5大气再分析产品(https://cds.climate.copernicus.eu/). 本文选取了5个气象变量, 分别是2 m处空气温度(TEM, K)、10 m风速(WS, m · s-1)、相对湿度(RH)、表面压力(SP, hPa)和边界层高度(BLH, m).气象数据的时间分辨率为月, 空间分辨率为0.25°×0.25°.
④ 地理数据:本研究使用的地理数据分别是植被归一化指数(NDVI)和SRTM DEM, 其中, NDVI数据来自LAADS网站(http://ladsweb.nascom.nasa.gov), 空间分辨率为1 km;SRTM DEM数据来自地理空间数据云网站(http://www.gscloud.cn), 空间分辨率为90 m.
由于研究数据的时间分辨率和空间分辨率不统一, 本文对原始数据进行了提取整合、投影转换、重采样获得统一的3 km×3 km空间分辨率的数据集.剔除空缺值后获得2019年1—12月共15226条有效数据.
3 模型与方法(Models and methods) 3.1 BP传播神经网络(BPNN)BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络, 其输出结果前向传播, 误差反向传播.BP神经网络一般由输入层、隐含层、输出层3层网络结构组成, 其过程主要分为两个阶段, 第一阶段是信号的前向传播, 从输入层经过隐含层, 最后到达输出层;第二阶段是误差的反向传播, 从输出层到隐含层, 最后到输入层, 依次调节隐含层到输出层的权重和偏置, 以及输入层到隐含层的权重和偏置(Li et al., 2017).
3.2 随机森林(RF)随机森林是一种基于Bagging和决策树的集成学习(Ensemble Learning)算法.它通过自助法(Bootstrap)重采样技术, 从原始训练样本N中有放回地抽取n个样本, 然后生成的多棵决策树组成随机森林, 新数据的分类结果按决策树投票多少形成的分数而定.随机森林集成了多棵决策树, 每棵树的建立依赖于独立抽取的样本(芦华等, 2020).
3.3 XGBoost模型XGBoost模型是在Gradient Boosting框架下实现的机器学习算法, 是集成算法中提升法(Boosting)的代表算法.集成算法通过在数据上构建多个弱评估器, 汇总所有弱评估器的建模结果, 以获取比单个模型更好的回归表现.XGBoost模型的思想是不断添加树(图 2), 每次添加一棵树, 就是学习一个新函数f去拟合上次预测的残差, 训练完得到k棵树, 每棵树会落到对应的一个叶子节点, 每个叶子节点对应一个分数, 将每棵树对应的分数加起来就是该样本的预测值.假设该模型中共有K棵树, 则整个模型在样本i上的预测结果见式(1).
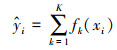
|
(1) |
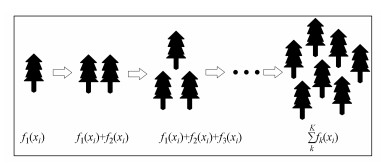 |
| 图 2 XGBoost模型建模过程 Fig. 2 XGBoost model modeling process |
式中, 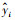
XGBoost算法具有以下优点:XGBoost在目标函数中加入了正则化项, 降低了模型的方差, 使学习出来的模型更加简单, 可以有效防止过拟合;XGBoost对损失函数进行了二阶泰勒展开, 使得模型精度更高;XGBoost支持并行化, 并且借鉴RF算法, 支持列抽样, 训练速度快.
3.4 XGBIDW模型XGBIDW模型是在XGBoost模型的基础上将时空信息作为模型输入.对于给定点, 其属性值Pd可由该点周围站点测量值反距离加权(IDW)表示, 时间属性Pt可由该点所在月份表示, 具体表示如下:
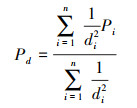
|
(2) |
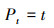
|
(3) |
式中, i为给定点的周围站点, t为给定点的月份.XGBIDW模型考虑了空间中一点的PM2.5值受周围邻域内其他站点的影响, 一定程度上可提高模型估算精度.
3.5 STXGB模型 3.5.1 Kriging原理① 区域化变量:研究区域可以看作是一种满足Kriging插值条件的区域化变量Q(x), x1, x2, …, xn是区域内PM2.5地面监测站点位置, Q(x1), Q(x2), …, Q(xn)是对应站点的PM2.5观测值.对于区域内某一点x0, 其空间属性Qd(x0)可以由Kriging法插值得到, 时间属性Qt可以用该点所在月份表示, 具体可表示为:
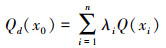
|
(4) |
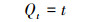
|
(5) |
式中, Qd(x0)为给定点的空间属性, λi为Kriging权重, Q(xi)为该点周围站点监测值, t为给定点的月份.
Kriging与IDW不同, 权重系数不是距离平方的倒数, 而是满足站点处估计值Qd(x0)与真实值Q(x0)之差最小的一套最优系数, 同时满足无偏估计的条件, 即:
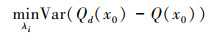
|
(6) |
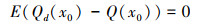
|
(7) |
② 变异函数:变异函数是克里金插值法的基础, 是用于描述PM2.5地面监测站点之间、监测站点与像素点之间空间关系的模型函数, 区域化变量Q(x)的变异函数可以用监测站点xi和xj观测值之差的半方差γ(xi, xj)表示(式(8)).
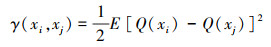
|
(8) |
③ 方程解算:在无偏和估计方差最小的情况下可以得到Kriging方程组式(9)、式(10).
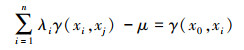
|
(9) |
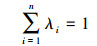
|
(10) |
式中, μ为拉格朗日乘数因子.求解上述方程组可以得到Kriging权重λi, 进而求得区域内任一点x0的估计值Qd(x0).
克里金法相比反距离加权法有诸多优势:克里金法可满足无偏和估计方差最小;变异函数作为一种定量描述空间相关性的统计学工具, 通过其自身结构和各项参数, 可充分反映空间数据的相关性, Kriging法通过计算样本的变异函数, 充分考虑了PM2.5站点数据的相关性;克里金法的估计结果精度优于反距离加权法(靳国栋等, 2003).
3.5.2 STXGB模型构建为了充分考虑PM2.5质量浓度估算中监测站点数据空间相关性问题, 提高PM2.5空间估算精度, 本文引入Kriging方法, 构建了一种时空XGBoost模型(STXGB), 为解决PM2.5估计中复杂的空间关系提供了新思路.将Kriging法计算得到的任一点空间位置估计值Qd, 以及该点时间位置Qt作为模型的输入变量, STXGB模型考虑了空间中任一点的PM2.5值受周围邻域内其他站点数值的影响.STXGB模型可以表示为式(11), 其结构见图 3.
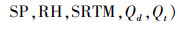
|
(11) |
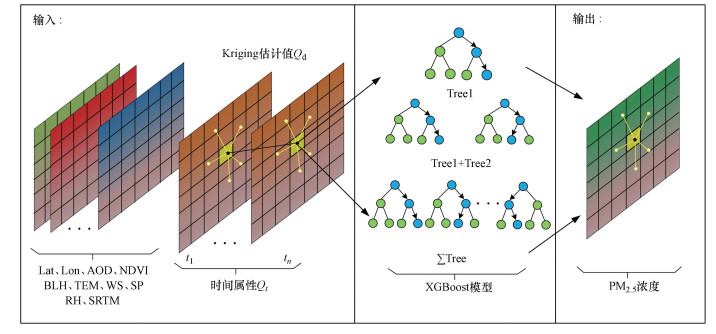 |
| 图 3 STXGB模型结构图 Fig. 3 STXGB model structure diagram |
式中, PM2.5为STXGB模型PM2.5估计值, f为机器学习模型, LAT为纬度, LON为经度.
3.6 精度评估为了充分评估STXGB模型的性能, 本文采用基于样本、站点和时间的十折交叉验证(10-CV), 并将计算结果与BPNN、RF、XGBoost、XGBIDW比较.根据模型预测结果分别计算决定系数(R2)、均方根误差(RMSE)、平均预测误差(MPE)3个指标来检验模型性能.相关系数(R)是研究变量之间线性相关程度的量, 决定系数(R2)反映的是因变量的变异中可由自变量解释部分所占的比例, 因此, 本研究选取决定系数作为模型评估的指标之一.各评价指标计算公式如下:
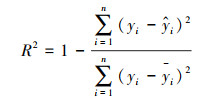
|
(12) |
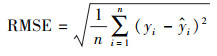
|
(13) |
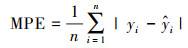
|
(14) |
式中, yi为观测值, yi为观测值的平均值, 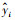
表 1显示了各机器学习模型的性能.在基于样本的交叉验证中, 5种机器学习模型的R2为0.77~0.92, 考虑站点数据相关性的XGBIDW模型和STXGB模型的R2均大于0.90, 其中, STXGB模型表现最佳;各模型的RMSE为6.51~11.38 μg · m-3, STXGB模型的RMSE值最低, 而BPNN模型的RMSE值最大(11.38 μg · m-3);MPE为4.26~8.07 μg · m-3, STXGB模型的MPE值最低为4.26 μg · m-3, 其次是XGBIDW模型的4.69 μg · m-3.
| 表 1 各模型结果对比 Table 1 Comparison of results of various models |
在基于站点的交叉验证中, 考虑地理相关性和时间变化的STXGB模型和XGBIDW模型的R2明显高于XGBoost、RF、BPNN等传统机器学习模型, 但相较于基于样本的交叉验证的R2值较低, 这是因为PM2.5在空间上的分布有明显的空间异质性;其中, STXGB模型的R2值最高为0.87, 其次是XGBIDW模型, BPNN模型表现最差;对比RMSE和MPE指标, STXGB模型和XGBIDW模型的RMSE和MPE值明显低于其他传统机器学习模型, STXGB模型表现最优, RMSE和MPE值分别为8.08 μg · m-3和5.25 μg · m-3, 这说明充分考虑站点数据相关性的STXGB模型在空间尺度上表现优异.
基于时间的交叉验证各模型表现相对较差, 这是因为PM2.5分布在时间尺度上有明显差异;各机器学习模型的R2为0.46~0.78, STXGB模型表现最优, R2值为0.78, 其次是XGBIDW模型, BPNN模型表现最差;对比RMSE和MPE指标, STXGB模型的RMSE和MPE值最低, 分别为7.09 μg · m-3和4.81 μg · m-3, BPNN模型的RMSE和MPE值最大达到了13.53 μg · m-3和10.08 μg · m-3, 这说明考虑时间变化的STXGB模型在时间尺度上表现优异.
图 4显示了BPNN、RF、XGBoost、XGBIDW、STXGB模型估算的PM2.5浓度与地面监测站点实测的PM2.5浓度拟合的散点密度图.由图 4可知, STXGB模型和XGBIDW模型优于BPNN、RF、XGBoost等传统机器学习模型, 原因是STXGB模型和XGBIDW模型考虑了站点数据相关性和时间变化, 能够更好地描述PM2.5的时空特征.STXGB模型和XGBIDW模型绘制的散点密度图的拟合线斜率均为0.97, 但STXGB模型的截距(1.08 μg · m-3)比XGBIDW模型截距(1.18 μg · m-3)小, 这表明STXGB模型的拟合效果最好, 原因是STXGB模型引入了Kriging法, 通过计算变异函数, 充分考虑了站点数据的空间相关性, 提高了PM2.5估算精度.BPNN估算的地面PM2.5质量浓度拟合曲线斜率最小, 截距最大, 严重低估了PM2.5值, 表现最差.值得注意的是, 5种机器学习模型拟合的散点密度图斜率均小于1, 可以认为机器学习模型在某种程度上低估了PM2.5浓度.综合对比5种机器学习模型可知, STXGB模型的预测性能最好, 其次是XGBIDW模型, 而BPNN在5个模型中的预测性能最差.
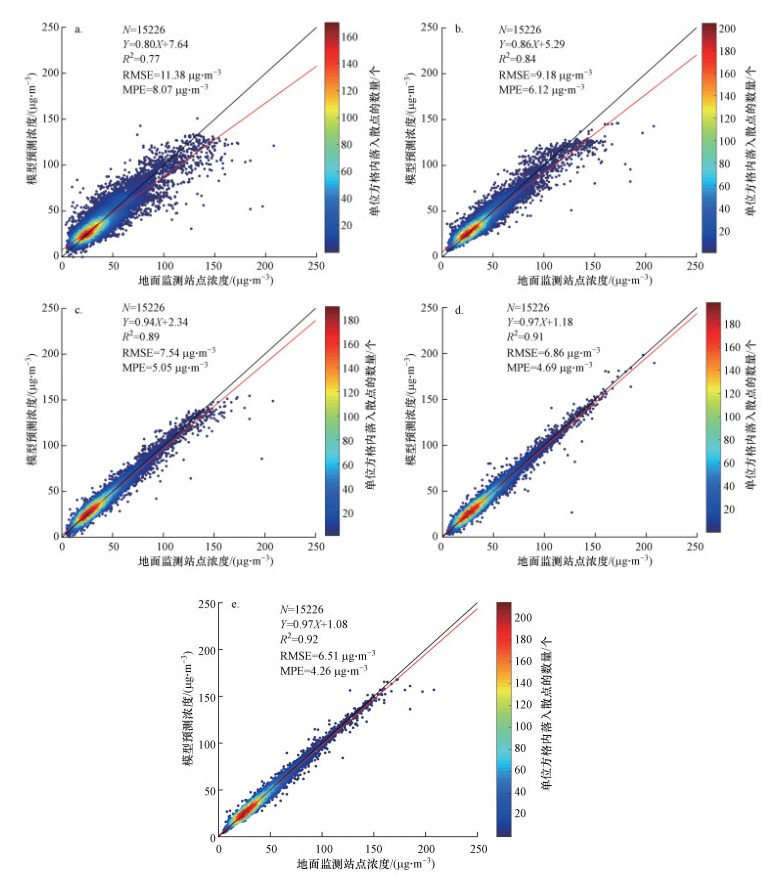 |
| 图 4 各模型散点密度图 (a.BPNN, b.RF, c.XGBoost, d.XGBIDW, e.STXGB) Fig. 4 Model scatter point density map (a.BPNN, b.RF, c.XGBoost, d.XGBIDW, e.STXGB) |
已有研究表明, 机器学习模型在不同季节表现有差异(Gupta et al., 2009), 这是由于不同季节的污染物来源不同造成的.本节以季节为尺度, 探究了STXGB模型在季节预测上的差异.按季节划分后, 获得春季数据(3—5月)3921条, 夏季数据(6—8月)3980条, 秋季数据(9—11月)4132条, 冬季数据(12月—次年2月)3198条.
表 2显示了STXGB模型在不同季节的预测结果, 图 5显示了STXGB模型在季节尺度上估算的PM2.5浓度和地面监测站点实测的PM2.5浓度拟合的散点密度图.基于样本的十折交叉验证表明, 冬季R2(0.89)最高, 也是RMSE(10.02 μg · m-3)和MPE(6.73 μg · m-3)最高的季节, 这可能是由于冬季地表温度与PM2.5相关性较高导致了R2较高(康俊锋等, 2020), 人为污染导致PM2.5质量浓度升高, 估算误差较大.相比之下, 夏季R2(0.76)最低, 也是RMSE(4.13 μg · m-3)和MPE(2.82 μg · m-3)最低的季节.夏季估算误差较低是因为频繁的降雨导致地面PM2.5质量浓度降低, 估算精度较高. 对于基于站点的交叉验证表现出相似的趋势, 但相较于基于样本的交叉验证, 模型精度略微降低, 这是因为PM2.5在季节尺度上空间分布显示出较强的空间异质性.春、夏、秋、冬4个季节的R2分别为0.66、0.57、0.77、0.82, 冬季的RMSE(12.06 μg · m-3)和MPE(8.73 μg · m-3)最高, 夏季的RMSE(4.97 μg · m-3)和MPE(3.18 μg · m-3)最低.总体而言, STXGB模型在季节尺度上表现优异, 能够预测PM2.5质量浓度在季节尺度上的分布.
| 表 2 STXGB模型不同季节预测结果 Table 2 STXGB model forecast results in different quarters |
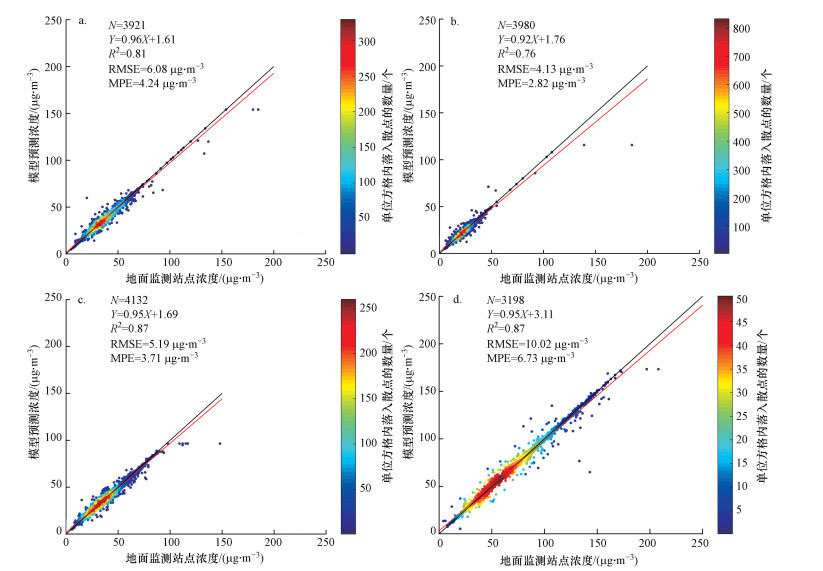 |
| 图 5 季节模型散点密度图 (a.春季, b.夏季, c.秋季, d.冬季) Fig. 5 Scatter plot of quarterly model |
图 6显示了STXGB模型估算的中国区域年均PM2.5质量浓度空间分布.由于中国西北部分地区AOD数据缺失, 导致在该地区难以获得空间连续的PM2.5浓度估算分布, 白色区域表示数据缺失.STXGB模型估算的PM2.5值与地面监测站点实测值分布趋势一致, 根据模型结果, 全国年均PM2.5质量浓度为27.5 μg · m-3.从空间上看, 中国东部地区污染比西部地区严重, 这与经济发展和城市化分布相一致.特别是华北地区, 污染物集中分布在河北南部、河南北部、山东西部, 平均浓度在70 μg · m-3以上, 原因是华北地区工业密集, 污染物排放严重.华中地区、四川盆地也有较大的空气污染, 这是因为华中地区经济发达, 人口密度大, 强烈的人类活动导致污染物排放增多, 四川盆地地形特殊, 不利于污染物的扩散.华南地区由于地理位置偏南, 地处沿海, 降雨量大, 空气污染较少, PM2.5平均浓度在30 μg · m-3以下, 低于全国年均浓度.此外, 新疆地区也出现了较为严重的空气污染, 原因是新疆塔克拉玛干沙漠沙尘暴频发, 空气质量差.
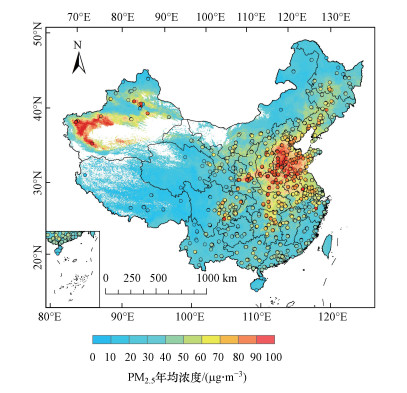 |
| 图 6 PM2.5年均浓度空间分布 Fig. 6 Spatial distribution of annual average concentration of PM2.5 |
图 7显示了STXGB模型估算的中国PM2.5质量浓度季度分布, 由于西北地区云层遮挡和高亮地表的影响, 卫星在这些地方难以获得连续的AOD数据, 造成该地区数据缺失严重(图中白色区域表示数据缺失), 尤其是春季和冬季.由图可知, PM2.5质量浓度空间分布具有显著的季节性.冬季污染最为严重, PM2.5平均浓度为49.9 μg · m-3, 污染物集中分布在中国中部, 原因是冬季燃煤导致污染物排放超标, 中部地区特殊的地理位置和不利于污染物扩散的气象条件导致PM2.5污染严重.夏季污染最轻, PM2.5平均质量浓度为18.9 μg · m-3, 低于年均PM2.5浓度, 原因是夏季降雨较多, 相对湿度较大, 有利于空气中的细颗粒物沉降.春季和秋季的PM2.5浓度相似, 平均浓度分别为30.68 μg · m-3和25.17 μg · m-3.除此之外, 新疆地区塔克拉玛干沙漠沙尘暴频发导致该地区空气PM2.5浓度常年偏高.
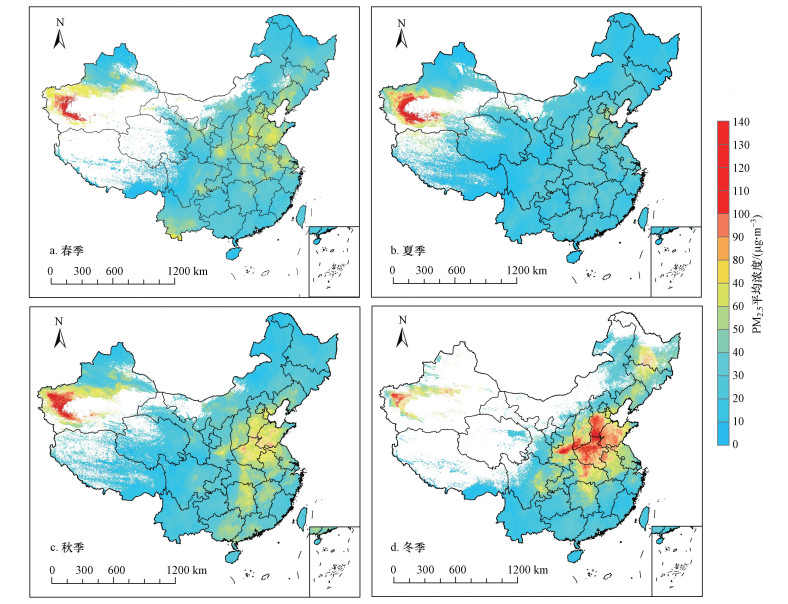 |
| 图 7 STXGB模型季度反演空间分布图 (a.春季, b.夏季, c.秋季, d.冬季) Fig. 7 Quarterly inversion spatial distribution map of STXGB model |
目前, 已有许多学者构建了不同类型的模型来提高PM2.5估算精度.例如, 康俊峰等(2020)构建了XGBoost模型, 该模型的决定系数R2为0.81;Li等(2017)提出了一种地理智能深度学习方法, 该模型基于样本和基于站点的十折交叉验证R2分别为0.88和0.82;杜震洪等(2020)构建了地理神经网络加权回归模型(GNNWR), 模型在训练集和测试集上的R2分别为0.914和0.831;Wei等(2020)构建的时空随机森林(STRF)模型的基于样本和基于站点的十折交叉验证R2分别为0.85和0.83.相较于先前的研究结果, 本文提出的STXGB模型基于样本和基于站点的R2分别为0.92和0.87, PM2.5估算精度有了较大提高.
综上, 本文提出的STXGB模型充分考虑了站点数据的空间相关性, 提高了PM2.5反演精度, 但仍存在一些不足需要继续研究.STXGB模型的调参复杂, 后续研究将考虑优化模型调参.同时, PM2.5的污染与诸多因素有关, 考虑更高精度的MODIS AOD数据以满足东部地区污染来源识别和变化趋势预测的需要将是今后工作的重点.
6 结论(Conclusions)1) STXGB模型相比传统机器学习模型表现最优, 其中, 基于样本、站点和时间的十折交叉验证R2最大, 分别为0.92、0.87、0.78;均方根误差(RMSE)、平均预测误差(MPE)最小.这表明STXGB模型在时间和空间尺度表现优异, 可以用来反演中国PM2.5浓度.
2) STXGB模型反演的2019年中国区域PM2.5年平均浓度空间分布结果表明, PM2.5污染主要分布在华北平原和新疆塔克拉玛干沙漠地区, 全国年均PM2.5质量浓度为27.5 μg · m-3.
3) STXGB模型在季节尺度上表现优异, 春、夏、秋、冬4个季节基于样本的交叉验证R2分别为0.81、0.76、0.87、0.89;冬季污染严重, PM2.5平均质量浓度为42.7 μg · m-3;夏季污染最轻, PM2.5平均质量浓度为18.9 μg · m-3.
Benas N, Beloconi A, Chrysoulakis N. 2013. Estimation of urban PM10 concentration, based on MODIS and MERIS/AATSR synergistic observations[J]. Atmospheric Environment, 79: 448-454. DOI:10.1016/j.atmosenv.2013.07.012 |
Chen G, Li S, Knibbs L D, et al. 2018. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information[J]. Science of the Total Environmental, 636: 52-60. DOI:10.1016/j.scitotenv.2018.04.251 |
陈辉, 厉青, 李营, 等. 2019. 京津冀及周边地区PM2.5时空变化特征遥感监测分析[J]. 环境科学, 40(1): 33-43. |
Chen W, Ran H, Cao X, et al. 2020. Estimating PM2.5 with high-resolution 1 km AOD data and an improved machine learning model over Shenzhen, China[J]. Science of the Total Environmental, 746(141093). DOI:10.1016/j.scitotenv.2020.141093 |
Christopher S, Gupta P. 2020. Global distribution of column satellite aerosol optical depth to surface PM2.5 relationships[J]. Remote Sensing, 12(12): 1985. DOI:10.3390/rs12121985 |
陈优芳, 周一敏, 赵昕奕. 2019. 基于卫星遥感AOD的华北地区2003-2014年PM2.5浓度时空分布特征[J]. 热带气象学报, 35(6): 822-30. |
Dong L, Li S, Yang J, et al. 2020. Investigating the performance of satellite-based models in estimating the surface PM2.5 over China[J]. Chemosphere, 256(127051). DOI:10.1016/j.chemosphere.2020.127051 |
杜震洪, 吴森森, 王中一, 等. 2020. 基于地理神经网络加权回归的中国PM2.5浓度空间分布估算方法[J]. 地球信息科学学报, 22(1): 122-35. |
付宏臣, 孙艳玲, 陈莉, 等. 2020. 基于AOD数据与GWR模型的2016年新疆地区PM2.5和PM10时空分布特征[J]. 环境科学学报, 40(1): 27-35. |
Gupta P, Christopher S A. 2009. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach[J]. Journal of Geophysical Research, 114(D14). DOI:10.1029/2008JD011496 |
郭新彪, 魏红英. 2013. 大气PM2.5对健康影响的研究进展[J]. 科学通报, 58(13): 1171-1177. |
靳国栋, 刘衍聪, 牛文杰. 2003. 距离加权反比插值法和克里金插值法的比较[J]. 长春工业大学学报(自然科学版), (3): 53-57. DOI:10.3969/j.issn.1674-1374-B.2003.03.017 |
康俊锋, 黄烈星, 张春艳, 等. 2020. 多机器学习模型下逐小时PM2.5预测及对比分析[J]. 中国环境科学, 40(5): 1895-905. DOI:10.3969/j.issn.1000-6923.2020.05.005 |
芦华, 谢旻, 吴钲, 等. 2020. 基于机器学习的成渝地区空气质量数值预报PM2.5订正方法研究[J]. 环境科学学报, 40(12): 4419-4431. |
刘林钰, 张永军, 李彦胜, 等. 2020. 基于深度学习的华东地区PM2.5浓度遥感反演[J]. 环境科学, 41(4): 1513-1519. |
李同文, 孙越乔, 杨晨雪, 等. 2015. 融合卫星遥感与地面测站的区域PM2.5反演[J]. 测绘地理信息, 40(3): 6-9. |
Li T, Shen H, Yuan Q, et al. 2017. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach[J]. Geophysical Research Letters, 44(23): 11985-11193. DOI:10.1002/2017GL075710 |
Li T, Shen H, Zeng C, et al. 2017. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment[J]. Atmospheric Environment, 152: 477-489. DOI:10.1016/j.atmosenv.2017.01.004 |
Maji K J, Ye W F, Arora M, et al. 2018. PM2.5-related health and economic loss assessment for 338 Chinese cities[J]. Environ Int, 121(1): 392-403. |
Pan B. 2018. Application of XGBoost algorithm in hourly PM2.5 concentration prediction[J]. IOP Conference Series: Earth and Environmental Science, 113(012127). DOI:10.1088/1755-1315/113/1/012127 |
邵琦, 陈云浩, 李京. 2018. 基于卫星遥感和气象再分析资料的北京市PM2.5浓度反演研究[J]. 地理与地理信息科学, 34(3): 32-38. DOI:10.3969/j.issn.1672-0504.2018.03.006 |
邵彦川, 王江浩, 葛咏. 2018. 基于地理加权回归克里金的中国PM2.5浓度空间制图方法[J]. 遥感技术与应用, 33(6): 1103-1111. |
Shao Y, Ma Z, Wang J, Bi J. 2020. Estimating daily ground-level PM2.5 in China with random-forest-based spatiotemporal kriging[J]. Science of the Total Environmental, 740(139761). DOI:10.1016/j.scitotenv.2020.139761 |
Wei J, Huang W, Li Z, et al. 2019. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach[J]. Remote Sensing of Environment, 231(111221). DOI:10.1016/j.rse.2019.111221 |
陶金花, 张美根, 陈良富, 等. 2013. 一种基于卫星遥感AOT估算近地面颗粒物的方法[J]. 中国科学: 地球科学, 43(1): 143-154. |
田宏伟, 师丽魁, 李梦夏. 2020. 两种地面PM2.5质量浓度遥感反演方法适用性比较[J]. 气象与环境科学, 43(3): 59-64. |
吴健生, 王茜. 2017. 基于AOD数据反演地面PM2.5浓度研究进展[J]. 环境科学与技术, 40(8): 68-76. |
夏晓圣, 陈菁菁, 王佳佳, 等. 2020. 基于随机森林模型的中国PM2.5浓度影响因素分析[J]. 环境科学, 41(5): 2057-2065. |
夏志业, 刘志红, 王永前, 等. 2015. MODIS气溶胶光学厚度的PM2.5质量浓度遥感反演研究[J]. 高原气象, 34(6): 1765-71. |
徐建辉, 江洪. 2015. 长江三角洲PM2.5质量浓度遥感估算与时空分布特征[J]. 环境科学, 36(9): 3119-27. |
杨立娟, 徐涵秋, 金致凡. 2018. MODIS卫星遥感估计福州地区近地面PM2.5浓度[J]. 遥感学报, 22(1): 64-75. |
于雪, 赵文吉, 孙春媛, 等. 2017. 大气PM2.5遥感反演研究进展[J]. 环境污染与防治, 39(10): 1153-8. |
Yuan Q, Shen H, Li T, et al. 2020. Deep learning in environmental remote sensing: Achievements and challenges[J]. Remote Sensing of Environment, 241(111716). DOI:10.1016/j.rse.2020.111716 |
赵滨, 刘斌. 2020. 基于Stacking的地面PM2.5浓度估算[J]. 环境工程, 38(2): 153-9. |
周亮, 周成虎, 杨帆, 等. 2017. 2000-2011年中国PM2.5时空演化特征及驱动因素解析[J]. 地理学报, 72(11): 2079-92. |
 2021, Vol. 41
2021, Vol. 41


