2. 寿县国家气候观象台, 中国气象局淮河流域典型农田生态气象野外科学试验基地, 寿县 232200
2. Shouxian National Climatology Observatory and Huai River Basin Typical Farm Eco-meteorological Experiment Field of CMA, Shouxian 232200
数值模式是开展空气质量预报的重要手段, 但由于初始场、气象场、排放源及模式本身的不足, 导致单个模式都有一定的不确定性, 且很多模式针对不同区域开发, 性能表现各异(谢敏等, 2012;周广强等, 2016;杨关盈等, 2017), 因此, 未来的趋势应是基于多模式的集成预报(姚文强等, 2017).多模式集成预报采用合理的方法集成, 能有效改进模式的整体预报效果, 有效提高空气质量预报的准确度(任万辉等, 2010).目前, 国内外已有一些研究将其应用在空气质量预报中, 并取得了较好的效果.例如, Djalalov等(2010)对7个模式O3和PM2.5预报的卡尔曼滤波集成进行了评估, 结果表明, 该方法显著提升了相关系数, 降低了预报偏差和均方根误差(RMSE);Loon等(2007)研究发现, 在欧洲采用7种模式的臭氧集成预报比任何单一模式更接近实况, 并能消除单一模式的不确定性;Monteiro等(2013)、Borrego等(2011)、Sicardi等(2012)、Baolei等(2017)分别利用偏差订正技术提升了多模式空气质量预报效果;王自发等(2009)利用多种集成预报技术方法, 对NAQPMS、CMAQ、CAMx等模式进行集成应用, 从总体上改善了预报的准确度;瞿元昊等(2018)采用多模式最优集成方法, 对中国和欧洲7个空气质量模式的PM2.5预报进行了集成释用, 显著提高了PM2.5污染等级预报、趋势预报和精度预报的效果;黄思等(2015)、潘锦秀等(2019)、Pagowski等(2006)分别将多模式集合预报和多元线性回归集成方法相结合, 从而减少了空气质量预报的不确定性, 且总体预报效果显著优于单模式;另有学者采用BP神经网络对多模式空气质量预报结果进行集成应用, 结果表明, 该方法的预报效果优于单个模式(张伟等2010;张恒德等, 2018).
安徽省位于中国东部腹地, 冬季易受高压控制, 降水较少, 盛行西北风并输送北方污染物, 导致雾霾事件多发(石春娥等, 2014;邓学良等, 2015;张海霞等, 2018), 而目前尚未见针对该地区PM2.5浓度的多模式集成预报方法研究.为提高安徽地区PM2.5质量浓度预报水平, 本文针对CUACE、WRF-Chem和CMAQ 3种模式在该地区PM2.5的预报结果, 采用多种集成方法进行释用, 并对结果进行评估, 以期寻找一种合理的集成订正方法, 并应用于日常空气质量预报预警业务.
2 资料与方法(Data and methods) 2.1 资料来源CUACE模式(CMA Unified Atmospheric Chemistry Environment)是由中国气象局开发的国家级雾霾数值预报业务系统, 能提供不同气象和空气质量要素预报(刘慧等, 2017;杨关盈等, 2018).该模式水平分辨率为15 km, 每日20:00起报, 预报时效为72 h, 预报产品主要包括SO2、NO2、PM10、CO、O3、PM2.5浓度及AQI、空气质量等级和首要污染物, 模式产品的时间分辨率为3 h.华东区域气象中心建立了基于WRF-Chem模式的“华东区域大气环境数值预报业务系统”(周广强等, 2015;常炉予等, 2016), 该系统预报区域以(32.5°N, 118.0°E)为中心, 水平分辨率为6 km, 水平网格数为360×400.另外, 华东区域中心同时开发了基于CMAQ模式的预报产品, 其预报范围与WRF-Chem模式一致.华东区域气象中心两个模式输出产品时间分辨率均为1 h.本文采用4种集成方法对中国气象局和华东区域气象中心下发的2017年2月—2018年2月3种模式(CUACE、WRF-Chem、CMAQ)72 h内逐3 h预报PM2.5浓度产品进行集成释用, 采用全国城市空气质量实时发布平台(http://106.37.208.233:20035/)获得的小时实测数据对上述3种模式产品及基于模式的集成预报产品进行效果评估.
2.2 集成方法介绍有研究表明, 集合成员的预报平均值比单模式预报结果更为接近实况值(Monache et al., 2003), 而采用权重平均方法能取得更好的效果(Mckeen et al., 2004;Pagowski et al., 2005), 多元线性回归集成、BP神经网络集成同样能改进模式预报结果(黄思等, 2015;张恒德等, 2018).本文针对安徽地区PM2.5的3种模式预报结果, 分别采用算术平均法、权重平均法、多元线性回归法和神经网络法进行集成应用和效果对比, 具体方法如下.
2.2.1 算术平均法(Mean)即在不区分各模式优劣的情况下, 以算术平均的方法获得集成预报值Fave(式(1)).

|
(1) |
式中, Fmodeli为第i个模式的预报值.
2.2.2 权重平均法(Weighted average)有研究表明, 当集合预报系统的集合成员较少时, 其集成效果可能并不总是最好(Mckeen et al., 2005), 因此, 采用给予不同模式不同权重的方法, 即:
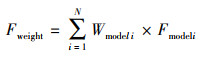
|
(2) |
式中, Wmodeli为模式i的权重因子, 所有模式权重因子之和为1.综合前人经验(张伟等, 2010;张恒德等, 2018), 采用预报前50 d预报偏差为权重, 即各模式权重值为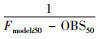

|
(3) |
对于每一天某时刻的预报值, 同样采用前50 d该时刻的CUACE、WRF-Chem和CMAQ预报结果作为回归集成因子, 求得对应时刻的预报值, 则该时刻的预报回归方程见式(4), 其中, ai表示训练阶段数据回归求得的第i个模式的权重系数, b为常数项.

|
(4) |
其原理是将模拟输出值和期望输出值的误差平方和作为神经网络的误差, 将误差反向传播, 不断循环, 直至误差满足要求(孙宝磊等, 2017;张恒德等, 2018).本文采用Python编程语言中机器学习模块Sklearn库中的多层感知机回归(MPLRegressor)方法, 即人工神经网络(Artifical Neural Network, ANN).为方便比较, 训练时长和时次与多元线性回归法相同, 即采用前50 d同一时刻的预报值和实况值进行训练.本研究中采用3层神经网络, 激活函数采用“relu”函数.
2.3 评估指标介绍 2.3.1 相关系数(r)、均方根误差(RMSE)和归一化平均偏差(NMB)选取r来反映预报值与实测值之间的线性相关程度;采用RMSE反映预报值与实测值之间的偏差, NMB反映预报值与实测值相比偏大或偏小的相对数值.具体公式如下:

|
(5) |

|
(6) |
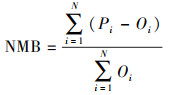
|
(7) |
式中, Pi为预报值, Oi为实测值, N为样本总数;P为预报平均值, O为观测平均值.
2.3.2 TS评分、空报率和漏报率对污染天气发生与否这样的“二元事件”预报效果评估常采用TS评分的方法.本研究采用预报评分(Threat Score, TS)、命中率(Hit Rate, HR)、空报率(False Alarm Ratio, FAR)、漏报率(Missing Rate, MR)的方法(石春娥等, 2013), 针对PM2.5浓度超过115 μg·m-3(中度污染等级, 低于重污染预警发布级别一个量级)的预报效果进行评估.具体公式如下:

|
(8) |

|
(9) |

|
(10) |

|
(11) |
式中, NA为预报和实测均达到中等污染等级次数;NB为预报达到而实测未达到的次数;NC为预报未达到而实测达到该等级的次数.
3 结果与讨论(Results and discussion) 3.1 全省总体预报效果评估表 1统计了2017年2月—2018年2月安徽省16个地市逐3 h的CUACE、WRF-Chem和CMAQ预报方法, 以及算术平均、权重平均、多元线性回归及人工神经网络误差统计结果.由表 1中相关系数(r)可见, 3个模式均呈显著相关(通过了显著性水平为0.01的显著性检验), 相较于单一模式, 4种订正方法除神经网络外均有所提升, 其中, 多元线性回归方法的提升效果最为明显, 相较于表现最优的WRF-Chem提升了0.07;从均方根误差(RMSE)来看, 除神经网络订正方法外, 其余3中方法的RMSE均在35 μg·m-3以下, 相较于单一模式均有所下降, 其中, 多元线性回归方法下降明显;从归一化平均偏差(NMB)来看, 除神经网络订正方法外, 其余方法的NMB均在±1%之间.
| 表 1 不同预报方法预报结果统计 Table 1 Performance evaluation of hourly forecasted PM2.5 mass concentration by different methods |
不同模式和订正方法因初始场、物理化学方案等不同, 其预报结果也存在不同偏差.图 1为研究期间各模式和各订正方法得到的预报值与观测值之间的偏差分布(预报小时值-实况小时值), 可见所有模式和订正方法得到的偏差均呈对称分布, 偏差均值(图中黑点)均接近0 μg·m-3, 但从箱体长度(1/4分位数~3/4分位数)和上下边缘来看, 多元线性回归订正方法的偏差分布最为集中, 其次为权重平均和人工神经网络.
 |
| 图 1 不同预报方法下安徽省PM2.5浓度预报偏差箱体分布 (上、下边缘横向表示上、下限值, 方框上、下限分别为75%和25%, 中心横向为50%, 圆点表示平均值) Fig. 1 Box plots of the bias between forecasted hourly PM2.5 mass concentrations by different methods and observations |
选取3~72 h逐3 h预报值中24 h的小时值与实况值进行对比, 计算不同预报方法的RMSE、NMB和r.图 2给出了RMSE的空间分布, 可见CUACE、WRF-Chem和CMAQ模式的预报值的RMSE能达到30 μg·m-3以内的地市仅有1~2个, 而相对于单一模式, 4种订正方法均能较有效降低RMSE, 采用多元线性回归、权重平均、算术平均和神经网络订正方法后RMSE能达到30 μg·m-3以内的地市个数分别为12、8、7、4个, 其中, 多元线性回归方法的降低效果最为明显, 在淮北地区RMSE也能降到40 μg·m-3以内, 优于其他订正方法.
 |
| 图 2 CUACE、WRF-Chem、CMAQ、算术平均、权重平均、多元线性回归和神经网络预报的24 h小时PM2.5浓度的RMSE空间分布 Fig. 2 RMSE spatial distributions of PM2.5 concentration at 24 h predicted by CUACE, WRF-Chem, CMAQ, Mean, Weighted, MLR and ANN |
图 3为选取3~72 h逐3 h预报值中24 h的小时预报值与实况值之间的NMB, 其中, 正三角形表示偏大, 倒三角形表示偏小.由图可知, 3种模式均在江南地区偏小, CUACE和CMAQ模式在沿江江北地区偏大, 部分城市预报值偏大50%以上, 而WRF-Chem模式预报值偏大或偏小的比例则在-50%~50%之间.4种订正方法均可将NMB降至-50%~50%, 而多元线性回归和神经网络的集成方法的预报值在全省范围内均能将NMB降至-25%~25%之间.
 |
| 图 3 CUACE、WRF-Chem、CMAQ、算术平均、权重平均、多元线性回归和神经网络预报的24 h的小时PM2.5浓度NMB空间分布 Fig. 3 NMB spatial distributions of PM2.5 concentration at 24 h predicted by CUACE, WRF-Chem, CMAQ, Mean, Weighted, MLR and ANN |
图 4为不同方法的24 h预报值与该时刻实况值的相关系数, 可见CUACE和WRF-Chem模式的r 值在除亳州和黄山以外的地方均能达到0.6以上, 好于CMAQ模式;而经过不同订正方法订正后, 算术平均、权重平均的效果相对最好, 有10个地市的相关系数在0.7~0.8之间, 多元线性回归方法的相关系数在8个地市能达到0.7~0.8之间, 略差于前两者.相对于表现最好的WRF-Chem模式来说, 权重平均方法在六安等7个城市的相关系数均提升, 提升率达到44%, 算术平均和多元线性回归方法的提升率分别为38%和25%, 神经网络方法的提升效果并不明显.
 |
| 图 4 CUACE、WRF-Chem、CMAQ、算术平均、权重平均、多元线性回归和神经网络预报的24 h的小时PM2.5浓度相关系数空间分布 Fig. 4 Correlation coefficient spatial distributions of PM2.5 concentration at 24 h predicted by CUACE, WRF-Chem, CMAQ, Mean, Weighted, MLR and ANN |
根据已有研究(邓学良等, 2015;石春娥等, 2018), 安徽地区霾分布具有明显的时空分布特征, 2010年, 沿淮淮北地区和江淮之间持续性区域霾过程显著多于沿江江南地区.这说明安徽省江北地区PM2.5浓度较高, 导致对这一地区进行预报值与实况值对比时, 其RMSE值也呈现出江北地区高于江南地区的地理分布特征, 特别是在一些高PM2.5污染易发的地区, 其RMSE也较高, 且易发生预报值严重偏离实况值的情况, 同时导致易出现NMB绝对值偏大的情况, 如CUACE和CMAQ等模式在亳州均出现NMB在50%以上的情况.而在安徽南部的黄山地区(全年PM2.5浓度较低), 其RMSE也较低.而从相关系数看, 3种模式在安徽中部地区效果较好, 在南部较差, 这也与安徽地区污染物浓度分布和变化特征有关系, 淮北地区和江淮之间以平原和丘陵为主, 冬季在偏北风影响下, 极易受北方污染输送影响, 因此, 模式对于这类情况易于模拟其变化趋势, 导致江北地区预报值与实况值相关性较好, 而江南南部为山区, 污染较少, 且以本地排放为主, 同时模式可能缺少详细的本地排放源等数据, 导致相关性较低.
3.3 时间序列预报效果检验分别选取淮北、合肥和芜湖(代表安徽省淮北地区、江淮之间和沿江江南地区), 对3个城市的RMSE、r和NMB进行分析.图 5为3个地市3~72 h逐3 h不同模式和订正方法的RMSE、r和NMB.从图 5可知, 在3个代表地区多元线性回归方法在不同时次内均能较好地降低RMSE和NMB, 而在提升相关系数方面的表现略差于权重平均的方法.另外从图 5可见, 在预报时次19~20、43~44及67~68 h 3个时段内, CUACE、WRF-Chem及CMAQ模式的RMSE有一个低值, 这是由于这个时间段对应北京时间下午15:00—16:00, 处于空气污染扩散条件最好的时段, 污染物浓度较低导致;但结合图 5可知, 这个时段淮北地区NMB也出现了负值, 表明3个模式均系统性地低估了该时刻的PM2.5浓度.从淮北、合肥和芜湖来看, 3个地区多元线性回归方法的NMB均在0附近波动, 表明其预报值更接近实况值, 对于模式的系统性偏差有较好的订正能力, 而算术平均和权重平均方法的预报值与实况值相关性虽然略高, 但其对于模式系统性偏差的纠错能力较差.由于神经网络集成方法受制于训练数据量的大小, 本文选取前50 d同一时刻的预报值与实况值进行训练, 且训练函数的模型参数对于集成效果的影响较大(张恒德等, 2018), 因而导致神经网络预报效果较差.
 |
| 图 5 淮北、合肥、芜湖地区各模式和订正方法预报的PM2.5浓度逐3 h预报值与观测值之间的RMSE、NMB和r Fig. 5 RMSE, NMB, and r between the observed and forecasted values of PM2.5 concentration by model and corrected forecast in Huaibei, Hefei, and Wuhu of Anhui Province |
按照《环境空气质量指数(AQI)技术规定》(HJ633—2012)中的标准, 对于PM2.5日均值超过115 μg·m-3的情况(中度污染等级, 重污染预警的前一个等级)进行统计分析.首先对于预报的小时值和实况小时值计算日均值, 并根据日均值计算CUACE、WRF-Chem和CMAQ模式及不同订正方法的TS评分、漏报率(MR)、空报率(FAR)和命中率(HR)等指标.表 2为全省所有16个站点的总体TS评分.
| 表 2 重污染天气下各模式和订正预报的PM2.5浓度TS评分结果 Table 2 TS results of PM2.5 concentration of each model and corrected forecast for heavy pollution weather |
从表 2可知, CUACE模式虽然命中率(HR)最高、漏报率(MR)最低, 但其空报率(FAR)也最高, 表明其倾向于在未出现中度以上污染天气时, 预报为中度以上污染, 导致其综合的TS评分最低.为弥补漏报率、空报率和命中率统计方法上的不足, 一般以TS评分来定量评估模式的预报效果.从最终TS评分来看, WRF-Chem在3种模式中表现最好, 而多元线性回归方法的效果优于其他订正方法.
4 结论(Conclusions)1) 各模式产品和订正产品的PM2.5预报值均与实况值能达到显著相关.4种订正方法均具有一定的订正能力, 但算术平均和权重平均方法易受3种模式预报结果的影响, 而多元线性回归和神经网络的方法则可以弥补这一不足.其中, 多元线性回归方法在不同时次和不同地区内, 与模式产品和其他订正产品相比, 整体上能够降低RMSE、NMB, 提升相关性, 相较于WRF-Chem模式的相关系数提升了0.07, 为0.68, RMSE从37.68 μg·m-3下降到29.50 μg·m-3, 下降幅度为21.7%, NMB下降了6%.
2) 从空间分布来看, 多元线性回归、权重平均、算术平均和神经网络方法均能降低模式预报的RMSE, 而多元线性回归方法能够将安徽省16个地市的PM2.5预报值的NMB降至-25%~25%之间, 但其在相关系数提升方面的表现不如权重平均和算术平均的订正方法.
3) 以淮北、合肥和芜湖为代表, 多元线性回归订正方法在3~72 h预报的不同时次内, 均能大幅度降低RMSE和NMB, 对于模式的系统性偏差有较好的订正能力, 但在提升相关系数r方面, 则略差于权重平均方法.对于重污染天气, 权重平均、多元线性回归和神经网络方法均能提升TS得分, 其中, 多元线性回归方法的TS评分为0.46, 高于其他订正方法.
4) 综合来看, 多元线性回归方法相较于算术平均和权重平均方法, 能够更为有效地降低不同时间和空间尺度的RMSE和NMB, 但对于相关系数的提升略差于权重平均的订正方法, 而神经网络受限于训练函数、隐含层节点数和训练样本长度的影响, 需要进一步细化训练方法, 才能有效提升预报效果.
Baolei L, Yuzhong Z, Yongtao H. 2017. Improving PM2.5 air quality model forecasts in China using a bias-correction framework[J]. Atmosphere, 8(12): 147-161. DOI:10.3390/atmos8080147 |
Borrego C, Monteiro A, Pay M T, et al. 2011. How bias-correction can improve air quality forecasts over Portugal[J]. Atmospheric Environment, 45(37): 6629-6641. DOI:10.1016/j.atmosenv.2011.09.006 |
常炉予, 许建明, 周广强, 等. 2016. 上海典型持续性PM2.5重度污染的数值模拟[J]. 环境科学, 37(3): 825-833
|
Djalalova I, Wilczak J, Mckeen S, et al. 2010. Ensemble and bias-correction techniques for air quality model forecasts of surface 03 and PM2.5 during the TEXAQS-II experiment of 2006[J]. Atmospheric Environment, 44(4): 455-467. DOI:10.1016/j.atmosenv.2009.11.007 |
邓学良, 石春娥, 姚晨, 等. 2015. 安徽霾日重建和时空特征分析[J]. 高原气象, 34(4): 1158-1166. |
环境保护部. 2016. 环境空气质量指数(AQI)技术规定(试行)(HJ633-2012)[S]. 北京: 中国环境科学出版社
|
黄思, 唐晓, 徐文帅, 等. 2015. 利用多模式集合和多元线性回归改进北京PM10预报[J]. 环境科学学报, 35(1): 56-64. |
Loon M V, Vautard R, Schaap M, et al. 2007. Evaluation of long-term ozone simulations from seven regional air quality models and their ensemble[J]. Atmospheric Environment, 41(10): 2083-2097. DOI:10.1016/j.atmosenv.2006.10.073 |
刘慧, 饶晓琴, 张恒德, 等. 2017. 环境气象业务数值模式预报效果对比检验[J]. 气象与环境学报, 33(5): 17-24. |
Mckeen S, Wilczak J, Grell G, et al. 2005. Assessment of an ensemble of seven real-time ozone forecasts over eastern North America during the summer of 2004[J]. Journal of Geophysical Research, 110(D21307). DOI:10.1029/2005JD005858 |
Monache L D, Stull R B. 2003. An ensemble air-quality forecast over western Europe during an ozone episode[J]. Atmospheric Environment, 37(25): 3469-3474. DOI:10.1016/S1352-2310(03)00475-8 |
Monteiro A, Ribeiro I, Tchepel O, et al. 2013. Bias correction techniques to improve air quality ensemble predictions: Focus on O3 and PM over Portugal[J]. Environmental Modeling & Assessment, 18(5): 533-546. DOI:10.1007/s10666-013-9358-2 |
Pagowski M, Grell G A, Devenyi D, et al. 2006. Application of dynamic linear regression to improve the skill of ensemble-based deterministic ozone forecasts[J]. Atmospheric Environment, 40(18): 3240-3250. DOI:10.1016/j.atmosenv.2006.02.006 |
Pagowski M, Grell G A, Mckeen S A, et al. 2005. A simple method to improve ensemble-based ozone forecasts[J]. Geophysical Research Letters, 32(7): 351-394. |
潘锦秀, 晏平仲, 孙峰, 等. 2019. 多元线性回归方法对北京地区PM2.5预报的改进应用[J]. 中国环境监测, 35(2): 48-57. |
瞿元昊, 许建明, Brasseur G, 等. 2010. 利用多模式最优集成方法预报上海PM2.5[J]. 环境科学学报, 38(9): 70-77. |
任万辉, 苏枞枞, 赵宏德. 2010. 城市环境空气污染预报研究进展[J]. 环境保护科学, 36(3): 9-11. |
Sicardi V, Arevalo G, Gassó S. 2012. Spatial and temporal bias correction to enhance air quality forecast over Spain[J]. Science of the Total Environment, 416(2): 329-342. |
石春娥, 吴照宪, 邓学良, 等. 2013. MM5与MM5-PAFOG模式区域雾预报效果评估比较[J]. 高原气象, 32(5): 1349-1359. |
石春娥, 邓学良, 杨元建, 等. 2014. 2013年1月安徽持续性霾天气成因分析[J]. 气候与环境研究, 19(2): 227-236. |
石春娥, 张浩, 杨元建, 等. 2018. 安徽省持续性区域霾污染的时空分布特征[J]. 中国环境科学, 38(4): 1231-1242. |
孙宝磊, 孙暠, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 37(5): 1864-1871. |
王自发, 吴其重, Gbaguidi A, 等. 2009. 北京空气质量多模式集成预报系统的建立及初步应用[J]. 南京信息工程大学学报(自然科学版), 1(1): 19-26. |
谢敏, 钟流举, 陈焕盛, 等. 2012. CMAQ模式及其修正预报在珠三角区域的应用检验[J]. 环境科学与技术, 35(2): 96-101. |
杨关盈, 邓学良, 吴必文, 等. 2017. 基于CUACE模式的合肥地区空气质量预报效果检验[J]. 气象与环境学报, 33(1): 51-57. |
杨关盈, 邓学良, 王磊, 等. 2018. 基于CUACE模式产品的订正方法比较研究[J]. 气象科学, 37(6): 839-844. |
姚文强, 王兆青, 铁治欣, 等. 2017. 多模式空气质量集成预报模型的研究[J]. 浙江理工大学学报, 37(3): 444-450. |
张海霞, 程先富, 陈冉慧. 2018. 安徽省PM2.5时空分布特征及关键影响因素识别研究[J]. 环境科学学报, 38(3): 1080-1089
|
张恒德, 张庭玉, 李涛, 等. 2018. 基于BP神经网络的污染物浓度多模式集成预报[J]. 中国环境科学, 38(4): 1243-1256. |
张伟, 王自发, 安俊岭, 等. 2010. 利用BP神经网络提高奥运会空气质量实时预报系统预报效果[J]. 气候与环境研究, 15(5): 595-601. |
周广强, 耿福海, 许建明, 等. 2015. 上海地区臭氧数值预报[J]. 中国环境科学, 35(6): 1601-1609. |
周广强, 谢英, 吴剑斌, 等. 2016. 基于WRF-Chem模式的华东区域PM2.5预报及偏差原因[J]. 中国环境科学, 36(8): 2251-2259. |
 2021, Vol. 41
2021, Vol. 41


