环境科学学报  2021, Vol. 41 Issue (4): 1565-1573
引用本文
姚红岩, 施润和. 2021. 基于周边站点优化选取的随机森林PM2.5小时浓度预测研究[J]. 环境科学学报, 41(4): 1565-1573.
Yao H Y, Shi R H. 2021. Research on hourly PM2.5 concentration prediction of random forest based on optimal selection of surrounding stations[J]. Acta Scientiae Circumstantiae, 41(4): 1565-1573.
基于周边站点优化选取的随机森林PM2.5小时浓度预测研究    [PDF全文]
姚红岩1,2,3, 施润和1,2,3,4,5    
1. 华东师范大学地理信息科学教育部重点实验室, 上海 200241;
2. 华东师范大学地理科学学院, 上海 200241;
3. 华东师范大学环境遥感与数据同化联合实验室, 上海 200241;
4. 华东师范大学资源与环境联合研究院, 上海 200062;
5. 华东师范大学崇明生态研究院, 上海 202162
收稿日期: 2020-07-01; 修回日期: 2020-08-31; 录用日期: 2020-08-31
基金项目: 国家重点研发计划项目（No.2016YFC1302602）；教育部哲学社会科学研究重大课题攻关项目（No.19JZD023）；上海市科委科技创新行动计划（No.19DZ1201505）；中央高校基本科研业务费项目
作者简介: 姚红岩(1995—), 女, E-mail: yaohongyan0327@126.com
通讯作者（责任作者）: 施润和, E-mail: rhshi@geo.ecnu.edu.cn
摘要：空气中的PM2.5是威胁人体健康的主要大气污染物，对其进行有效预测和及时预警具有重要意义.大量研究表明，纳入周边站点信息的随机森林模型在单站点PM2.5预测中显示出良好的效果，但在周边站点选取问题上目前尚缺乏针对性研究，部分选取方法带有主观性.本文提出了一种基于时间滞后互相关分析的周边站点优化选取方法，并以上海十五厂空气质量监测站（国控站）为例，构建了预测该站未来1~24 h PM2.5浓度的随机森林回归模型集，比较分析了预测模型中各输入因子的重要性.研究发现，预测站点当前PM2.5浓度值对未来1~16 h的预测最为重要，而气象要素中的风向则对于未来17~24 h的预测重要性最高；周边站点PM2.5信息随着预测时间的延长，其重要程度排名有明显提升，且不同站点对不同时间预测的影响具有显著差异，在建模时应区别对待，优化选取.比较结果表明，使用本文方法选取周边站点建立的预测模型不仅在RMSE等精度指标上具有一定优势（12 h和24 h预报RMSE分别降低11.8%和13.3%），还在有实用价值的污染事件空报率上有明显降低（12 h和24 h预报空报率分别降低16.1%和25.6%），具有业务应用潜力.
关键词：时间滞后互相关    时间序列    大气污染物    机器学习    
Research on hourly PM2.5 concentration prediction of random forest based on optimal selection of surrounding stations
YAO Hongyan1,2,3, SHI Runhe1,2,3,4,5    
1. Key Laboratory of Geographical Information Science, Ministry of Education, East China Normal University, Shanghai 200241;
2. School of Geographic Sciences, East China Normal University, Shanghai 200241;
3. Joint Laboratory for Environmental Remote Sensing and Data Assimilation, East China Normal University, Shanghai 200241;
4. Joint Research Institute of Resources and Environment, East China Normal University, Shanghai 200062;
5. Institute of Eco-Chongming, East China Normal University, Shanghai 202162
Received 1 July 2020; received in revised from 31 August 2020; accepted 31 August 2020
Abstract: PM2.5 is a major air pollutant that threatens human health, and it is significant to be effectively predicted and promptly warned. Many studies have shown that the Random Forest model (RF) has good results in the prediction of PM2.5 concentration at a single station by incorporating the information of surrounding stations. However, the research on the selection of surrounding stations is lack of pertinence, and some existing selection methods are subjective. We proposed a method for optimizing the selection of surrounding stations based on Time-Lag Cross-Correlation (TLCC) analysis in this research. Taking the air quality monitoring station (national-level station) of Shanghai Shiwuchang as an example, a set of RF regression models were constructed to predict the PM2.5 concentration of the station in the next 1 to 24 hours, and the importance of each input factor in the prediction model was compared and analyzed. We found that the current PM2.5 concentration of the prediction station would significantly impact the prediction of the next 1 to 16 hours, while the wind direction was crucial for the prediction of the next 17 to 24 hours. As the forecast time increased, PM2.5 concentration of the surrounding stations significantly improved in importance ranking, and the impact of different stations was significantly different when forecasting at different times. Therefore it was treated differently when modeling. The comparison results showed that the prediction model established by the method of selected surrounding stations proposed in this paper not only had certain advantages in accuracy (12-hour and 24-hour forecast RMSE decreased by 11.8% and 13.3%), but the false alarm ratio also decreased significantly (the forecasted false alarm ratio for 12 hours and 24 hours dropped by 16.1% and 25.6%). The study has practical value and potential applications in predicting and prewarning air pollution.
Keywords: time lag cross-correlation    time series    atmospheric pollutants    machine learning    
1 引言(Introduction)

PM2.5是空气动力学直径小于2.5 μm的细颗粒物总称, 可携带大量有害物质穿透肺泡进入血液, 直接危害人体健康.已有研究表明, PM2.5与心血管及呼吸疾病死亡率之间具有强相关关系(Pope Ⅲ et al., 2002;Liu et al., 2019; Zhang et al., 2019), 也是导致肺癌的已知危险因素.PM2.5来源复杂, 变化快速, 预测难度大.及时准确预测PM2.5浓度并采取针对性干预措施对降低其健康风险具有重要意义.

PM2.5浓度预测方法可分为数值模拟和统计建模两类.前者如WRF-CMAQ(Yang et al., 2019), 可以从物理机制上解释污染物的生成及传输等过程, 但通常需要进行大量参数化工作, 模型驱动困难.近年来, 我国环境空气质量监控站点数量在不断增加, PM2.5浓度监测网的日趋完善, 为基于统计模型的PM2.5浓度预测创造了有利条件.由于PM2.5的来源及传输过程复杂多变, 线性统计模型(彭斯俊等, 2014)的预测精度往往较低, 而新兴的机器学习模型则在表达PM2.5浓度与气象环境参数之间的复杂关系上显示出更好的效果.许多学者将决策树模型(Pan, 2018)、神经网络(Biancofiore et al., 2017; Qi et al., 2019)、ARIMA+ANN(Babu et al., 2014; Büyükşahin et al., 2019)、ARIMA+SVM(Wang et al., 2017)等机器学习模型或混合模型用于不同地区、不同预测时长的PM2.5浓度预测中, 取得了较好的预测效果.其中, 随机森林模型(Random Forest)不仅具有良好的泛化能力, 还能评估特征重要程度, 也被应用于PM2.5浓度预测(Yu et al., 2016; 杜续等, 2017; 侯俊雄等, 2017; Danesh Yazdi et al., 2020)及相关重要特征的选取与比较研究中(Feng et al., 2019; Zamani Joharestani et al., 2019; 夏晓圣等, 2020).

考虑到PM2.5在大气中的输送过程, 有必要将周边站点的PM2.5浓度监测数据纳入到PM2.5浓度预测模型中以提高预测准确性, 但在周边站点选取方面尚无公认方法.Li等(2017)以行政区划作为周边站点的空间范围；Zhao等(2019)以预测站点为中心, 选取距离最近的5个站点数据作为空间信息输入；Feng等(2015)通过气团轨迹分析得到研究区的污染输入路径, 在各个路径中人为选取一个站点作为空间输入；Bai等(2019)通过对不同空间窗口周边站点与预测站点的相关性进行敏感性分析, 确定平均相关系数最大的距离作为最佳空间范围.可见, 在现有单站点PM2.5浓度预测模型中, 研究者在周边站点选取上采用各自的方法, 但部分方法带有一定主观性.

由于盛行风向的存在, 对预测有贡献周边站点的空间分布形状通常是不规则的, 直接从空间上定义周边站点范围的难度较大, 并且难以保证所选取的周边站点对预测站点开展PM2.5浓度预测具备良好的代表性和全面性.因此本文提出一种基于时间滞后互相关分析的周边站点优化选取方法, 即根据周边站点与预测站点PM2.5小时浓度时间序列在时间维上的滞后关系, 优先选取与预测站点特定时刻PM2.5浓度预测具有高相关的周边站点, 摒弃低相关站点, 并进一步对空间上过于密集的周边站点进行筛选, 从而实现周边站点的优化选取.本文以上海十五厂国控环境空气质量监测站为例, 预测时长取1~24 h, 运用随机森林模型建立考虑周边站点的不同预测时长PM2.5浓度预测模型集, 并对预测结果进行比较与评价.

2 研究区与数据源(Research area and data source)

上海是中国的经济发展中心, 拥有2400多万常住人口, 2012年被《国家环境保护“十二五”规划》划入大气污染防治重点区域.本研究以位于上海市中心的十五厂空气质量监测站(国控站编号1142A)作为研究对象, 对其未来1~24 h的PM2.5浓度进行预测.上海东面临海, 属于亚热带季风气候, 冬季盛行西北风, 夏季盛行东南风.PM2.5来源包括本地排放和外来输送, 其中外来输送占比超过50%, 以江苏、浙江、安徽、山东等省为主(薛文博等, 2016).

本文的PM2.5浓度数据为上海、江苏、浙江、安徽、山东、山西、河南、河北七省一市各空气质量监测国控站自2015年1月1日0:00—2018年8月31日23:00的逐小时浓度数据, 来自中国环境监测总站和各省市环境监测中心.同期逐小时气象数据包括气温、风速和风向3个指标, 来自上海虹桥气象站.对于PM2.5浓度数据与气象数据中的部分离散缺失值, 主要采用最邻近时间线性插值方式予以插补.部分站点PM2.5浓度监测数据缺失严重, 难以通过插值方式保证数据质量, 此类站点直接予以剔除.

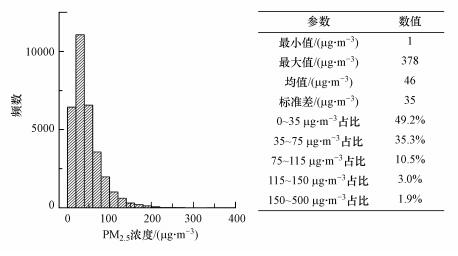图 1 十五厂空气质量监测站PM2.5小时浓度直方图和主要统计指标 Fig. 1 Histogram and main statistical indicators of PM2.5 hourly concentration in the Shiwuchang Air Quality Monitoring Station
3 研究方法(Methods) 3.1 单站点时间序列分析

本研究开展的单站点时间序列分析是指计算1142A站点时间序列的自相关系数acfn和偏相关系数pacfn, 其中n为时间窗口.自相关系数acfn只考虑t与t+n两个时刻PM2.5浓度数据的相关系数, 可通过acfn来判断单站点时间序列是否具有时间自相关特性.pacfn避免了在这两个时刻之间的数据(即t+1至t+n-1)对相关性分析的影响, 通过比较不同n值下的pacfn, 可获取最适宜的n作为预测的时间窗口.

3.2 多站点时间滞后互相关分析

周边站点与预测站点PM2.5浓度时间序列之间的时间滞后主要反映在污染事件发生时, 不同站点的PM2.5浓度会在不同时刻先后升高, 它们之间存在明显的时间差.本文对周边站点与预测站点的PM2.5浓度时间序列进行时间滞后互相关分析(Time Lags Cross Correlation, TLCC)来获取站点之间时间差的统计规律.

首先, 预测站点取以t0为起始时刻的PM2.5浓度时间序列X(t0), 将周边第i个站点的时间序列向左或向右平移n小时得到Xi(t0±n), 计算两条时间序列的相关系数, 使相关系数达到最大的n即为两个时间序列的时间差.若n > 0, 表示在统计上, 站点i发生污染n个小时后, 预测站点也发生污染, 即站点i可为预测站点n小时后的预测提供信息.考虑到预测站点n小时后的浓度与预测站点n-1小时的浓度密切相关, 而n-1小时的浓度又与时间差为n-1的站点相关, 依次可一直类推至n=1.因此, 在站点选取时应选取时间差从1~n小时的全部站点作为空间信息输入.当n较大时, 类推多步后的站点与预测站点的相关性会明显降低, 为保证周边站点选取的有效性, 本研究中进一步加入相关系数大于0.2的约束条件.

此外, 由于空间距离较近的周边站点的PM2.5浓度时间序列往往相关性高, 存在信息冗余.本研究采用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)密度聚类方法对周边站点进行聚类处理, 借助编程软件python中的DBSCAN函数, 以轮廓系数为指标, 调节邻域阈值和类别最小样本数, 实现站点空间聚类, 每一类中仅保留上述TLCC分析中与预测站点相关系数最大的站点.

3.3 随机森林回归模型及特征的重要性分析

本研究使用随机森林(Random Forest, RF)回归模型进行PM2.5浓度预测.RF通过构造多棵独立的决策树并对结果取平均来解决过拟合的问题, 具有良好的泛化能力.树模型通过寻找最佳分裂点获得最优点的方式适用于包含时间、风向等标签特征数据的建模.随机森林采用有放回随机取样, 因此对每棵决策树而言, 约有1/3训练样本不会被抽取, 这部分样本被称作袋外样本, 其得分可用来对模型性能进行无偏估计, 结果与需要大量计算的交叉验证相似, 因此可直接参考袋外样本的得分来挑选最佳模型结构, 降低了计算量, 这是随机森林的重要优势之一.

RF还具备评估特征的重要程度的功能.在对一棵树进行训练时, 分别对每个特征增加噪声, 计算增加噪声前后袋外样本得分的差值, 差值越大, 说明这一特征对决策树影响越大, 多棵树的平均得分差值可作为衡量特征重要性的指标, 直观地表示各个特征在预测中发挥的作用的大小.本研究将利用这一功能来分析对比不同因子对PM2.5浓度预测的重要性.

本研究中, 模型输入数据包括预测站点PM2.5前序时刻浓度数据、筛选的周边站点PM2.5浓度数据、风向、风速、温度、日期和时间等, 模型输出是预测站点第t小时的PM2.5浓度(t从1~24).模型主要参数包括决策树个数、最大特征个数和树的最大深度, 采用网格搜索的方法, 以袋外样本得分为指标对上述参数进行优化.

3.4 预测结果评价指标

常用的预测模型评价指标如RMSE(Root Mean Square Error)、MAE(Mean Absolute Error)等可对模型所有输出的PM2.5浓度逐小时预测结果进行统计计算, 得到量化精度指标.考虑到其计算时各次预测的权重均相同, 无法针对性地反映出实际应用中更关注的高污染事件的预测精度, 因此本研究还针对PM2.5污染事件采用空报率和漏报率对预测结果进行评价.污染事件的阈值参照我国环境空气质量标准取75 μg·m-3.考虑到污染事件突发时, 原来局部平稳的时间序列被打破, 预测结果往往会存在较大偏差, 因此在预测结果上加入10 μg·m-3的容差.也就是说, “空报率”是指在预测结果大于75 μg·m-3的时刻中, 实际观测值却小于65 μg·m-3所占的比例；“漏报率”是指在实际观测值大于75 μg·m-3的时刻中, 预测值却小于65 μg·m-3所占的比例.

4 结果与分析(Results and Analysis) 4.1 时间序列分析与周边站点选取

单站点PM2.5浓度数据正态分布检验(Kolmogorov-Smirnov test)的p值小于0.05, 呈非正态分布, 因此本文将采用Spearman秩相关系数来衡量相关性, 完成自相关系数、偏自相关系数和时间滞后互相关的计算.

计算预测站点PM2.5小时浓度时间序列的自相关系数和偏自相关系数, 绘制出自相关图(图 2a)和偏自相关图(图 2b).可见, 自相关图拖尾, 表示该时间序列具有较强的自相关性；偏自相关图 2阶截尾, 表示该时间序列具有2阶偏自相关性, 即当前状态与之前两个小时的状态有关.因此, 若要进行超过2 h的预测, 则预测站点自身的时间序列无法提供足够信息, 需要考虑周边站点.

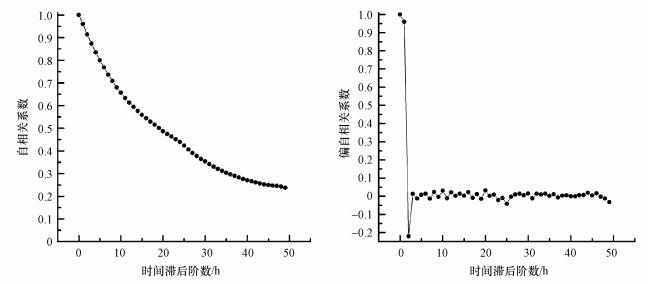图 2 预测站点时间序列分析的自相关图(a)和偏自相关图(b) Fig. 2 Autocorrelation (a) and partial autocorrelation (b) of time series analysis of the predicted station

使用TLCC方法对所有周边站点逐一进行分析.此处以连云港市环境监测站点(国控站编号1173A)为例, 说明分析结果.图 3是1173A站与预测站点的时间滞后互相关图.图中横坐标表示对1173A站的时间序列进行平移的小时数, 负数为左移, 正数为右移.由结果可知, 当两站点的时间差为12 h时(虚线处), 即1173A站的时间序列向未来移动12 h后, 与预测站点时间序列的相关系数达到最大值.因此可以认为, 1173A站的PM2.5浓度时间序列对预测站点12 h后的PM2.5浓度预测有较大贡献.

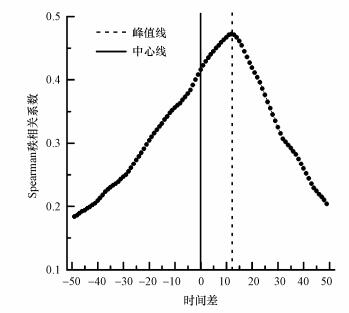图 3 站点1173A与预测站点的时间滞后互相关图 Fig. 3 Time lag cross-correlation diagram between station 1173A and the predicted station

对所有周边站点和预测站点的PM2.5浓度时间序列两两进行TLCC分析, 得到周边站点与预测站点呈最大相关性时的时间差分布.如图 4所示, 位于预测站点南方的站点与预测站点的时间差通常为负, 表示这些站点的时间序列往往晚于预测站点, 对预测站点的PM2.5浓度预测贡献不大；而位于预测站点北方的站点则与预测站点的时间差通常为正, 表示这些站点的时间序列往往早于预测站点, 对预测站点未来PM2.5浓度的预测更具参考性, 且时间差随距离增加而增大, 与上海市污染物空间来源情况及其扩散规律相吻合.

图 4 各站点与预测站点最大相关系数的时间差分布图 Fig. 4 Difftime distribution diagram of the maximum correlation coefficient between each station and the predicted station

在对预测站点进行未来第n小时预测时, 若周边站点的时间差位于为[0, n], 且与预测站点之间的相关系数大于0.2, 即选取该站点.同时, 由于空气环境质量监测站主要建在人口密集的城市, 导致城市区域站点之间距离较近, 监测值时间序列相关性高, 存在信息冗余, 本文使用DBSCAN进行聚类, 结果如图 5a所示, 436个站点共分为113类, 不同颜色代表不同类别, 在每个类别中选取与预测站点在第n小时时间差上相关系数最高的入选站点(图 5b), 从而减少冗余.图 6为当n为12时, 即预测目标站点未来第12小时的PM2.5浓度时所选取周边站点的空间分布情况.

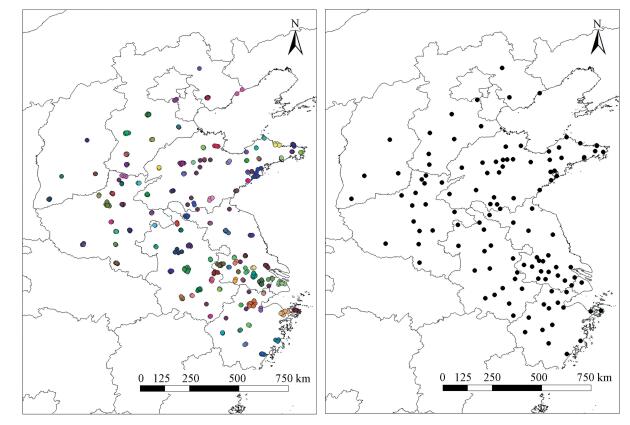图 5 周边站点DBSCAN密度聚类图(a)及筛选结果图(b) Fig. 5 DBSCAN clustering(a) and selection(b) of surrounding stations

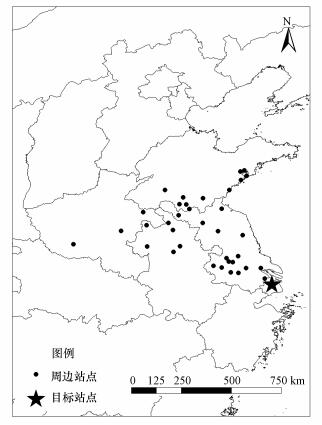图 6 预测第12 h PM2.5浓度时所选取的周边站点分布图 Fig. 6 Distribution diagram of selected surrounding stations when the PM2.5 concentration at 12 h is predicted
4.2 特征的重要性分析

基于随机森林模型对预测站点未来1~24 h PM2.5浓度预测的各特征变量进行重要性分析.考虑的特征变量包括气象因子、周边选取站点的PM2.5浓度时间序列、预测站点自身当前、前1 h和前2 h的PM2.5浓度小时浓度数据, 以及时间标签.考虑到随机森林的袋外样本可对模型性能进行无偏估计的性质, 数据集划分将采用简单划分法, 并且时间序列具有强自相关性, 因此要确保训练集与测试集在时间上的独立性, 故将时间序列数据集按时间先后排序后, 取前70%为训练集用于模型训练及参数调整, 后30%为测试集用于对模型预测结果进行测试.因篇幅原因, 图 7展示了8个特定预测时刻下, 4个重要程度最高的特征.可见, 在第1~16 h预测中, 预测站点当前PM2.5浓度排在首位, 贡献最大, 但随预测小时数的增加, 风向的重要性排到首位.

图 7 不同预测时刻4个重要程度最高的特征排序 Fig. 7 The 4 most important features at different prediction times

观察不同预测时刻10个重要程度最高的周边站点分布(图 8)可见, 站点的空间位置随预测时刻的增加逐渐向预测站点西北方向延伸, 延伸方向与上海非本地污染物输送的主导方向一致.

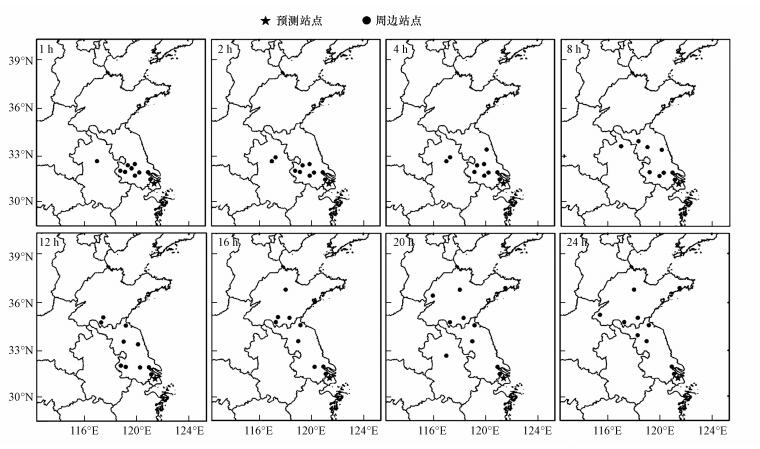图 8 不同预测时刻10个重要程度最高的周边站点分布图 Fig. 8 Distribution diagram of the 10 most important surrounding stations at different prediction times
4.3 预测结果的比较与分析

为了比较不同周边站点选取方案对预测站点PM2.5浓度预测的影响, 构建了不考虑周边站点、按半径50 km和100 km缓冲区范围选取站点和本文TLCC方法选取站点的4种方案, 对预测站点进行1~24 h预测, 得到不同预测时刻的精度指标RMSE和MAE如表 1和图 9a所示.可见, 考虑周边站点有助于降低预测误差, 且随着预测时间的增加, 各方案建立的随机森林模型的预测误差都呈增加趋势, TLCC方案总体上优于其它方案, 尤其在12~24 h预测中更为明显, 12 h和24 h预报RMSE分别降低11.8%和13.3%.

表 1 十五厂空气质量监测站在不同站点选取方案下的1~24小时预测精度对比 Table 1 The 1~24 hour prediction accuracy of Shiwuchang Air Quality Monitoring Station under different station selection schemes

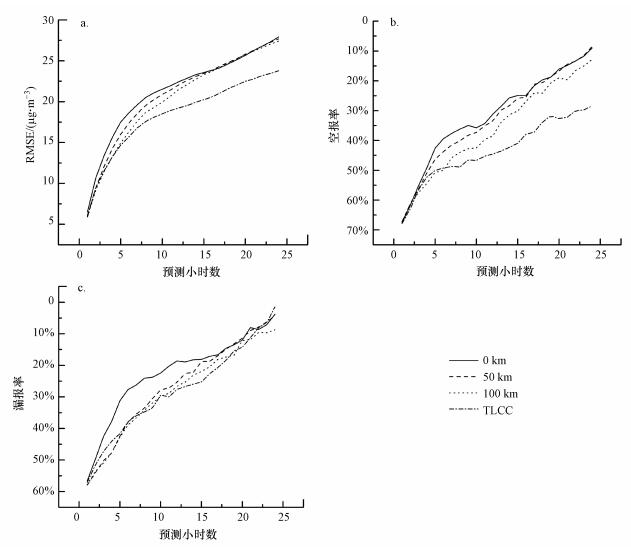图 9 各周边站点选取方案的预测性能比较(a.RMSE, b.空报率, c.漏报率) Fig. 9 Prediction performance under different selection schemes of surrounding stations

进一步以PM2.5浓度达到75 μg·m-3作为污染事件的阈值, 从实用性角度考察各方案的空报率和漏报率(图 9b、9c).可见, 在空报率方面TLCC方案明显优于其它方案, 12 h和24 h预报空报率分别降低16.1%和25.6%, 而在漏报率上与其它考虑周边站点的方案相似.

5 结论(Conclusions)

研究结果表明, 本方案选取站点的空间分布特点与上海非本地大气污染物的输送特点相附和, 且在1~24 h PM2.5浓度预测的平均误差和空报率方面均优于不考虑周边站点和按50 km或100 km半径缓冲区确定周边站点的方案, 尤其在12~24 h预测中性能优势更为明显.预测站点当前PM2.5浓度在短时预测中较重要, 随预测时刻的推移, 风向和周边站点PM2.5浓度重要性逐渐提高.而时间和温度、风速特征的重要性较低.

本方法中PM2.5浓度数据来自空气环境质量监测站, 更适用于周边站点充裕的PM2.5浓度预测.本文研究重点为周边站点的选取问题, 因此忽略了其日内变化和局地实际干扰因素等, 这可能是导致漏报率无明显改进的原因之一, 下一步将对漏报污染事件进行深入剖析, 同时将细化研究气象条件对周边站点选取方案的影响, 并进一步研究更多站点, 以探索本方案的普适性.

致谢: 感谢中国科学院地理科学与资源研究所、中国科学院资源环境科学数据中心提供基础地理数据.
参考文献
Büyükşahin Ü Ç, Ertekin Ş. 2019. Improving forecasting accuracy of time series data using a new ARIMA-ANN hybrid method and empirical mode decomposition[J]. Neurocomputing, 361: 151-163. DOI:10.1016/j.neucom.2019.05.099
Babu C N, Reddy B E. 2014. A moving-average filter based hybrid ARIMA-ANN model for forecasting time series data[J]. Applied Soft Computing, 23: 27-38. DOI:10.1016/j.asoc.2014.05.028
Bai K, Li K, Chang N, et al. 2019. Advancing the prediction accuracy of satellite-based PM2.5 concentration mapping: A perspective of data mining through in situ PM2.5 measurements[J]. Environmental Pollution, 254: 113047. DOI:10.1016/j.envpol.2019.113047
Biancofiore F, Busilacchio M, Verdecchia M, et al. 2017. Recursive Neural Network model for analysis and forecast of PM10 and PM2.5[J]. Atmospheric Pollution Research, 8(4): 652-659. DOI:10.1016/j.apr.2016.12.014
Danesh Yazdi M, Kuang Z, Dimakopoulou K, et al. 2020. Predicting fine particulate matter (PM2.5) in the greater London area: an ensemble approach using machine learning methods[J]. Remote Sensing, 12(6): 914. DOI:10.3390/rs12060914
杜续, 冯景瑜, 吕少卿, 等. 2017. 基于随机森林回归分析的PM2.5浓度预测模型[J]. 电信科学, 33(7): 66-75.
Feng R, Zheng H, Gao H, et al. 2019. Recurrent Neural Network and random forest for analysis and accurate forecast of atmospheric pollutants: A case study in Hangzhou, China[J]. Journal of Cleaner Production, 231: 1005-1015. DOI:10.1016/j.jclepro.2019.05.319
Feng X, Li Q, Zhu Y, et al. 2015. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation[J]. Atmospheric Environment, 107: 118-128. DOI:10.1016/j.atmosenv.2015.02.030
侯俊雄, 李琦, 朱亚杰, 等. 2017. 基于随机森林的PM2.5实时预报系统[J]. 测绘科学, 42(1): 1-6.
Li X, Peng L, Yao X, et al. 2017. Long Short-Term Memory Neural Network for air pollutant concentration predictions: Method development and evaluation[J]. Environmental Pollution, 231(1): 997-1004.
Liu C, Chen R, Sera F, et al. 2019. Ambient particulate air pollution and daily mortality in 652 cities[J]. New England Journal of Medicine, 381(8): 705-715. DOI:10.1056/NEJMoa1817364
Pan B. 2018. Application of XGBoost algorithm in hourly PM2.5 concentration prediction[J]. IOP Conference Series: Earth and Environmental Science, 113: 012127. DOI:10.1088/1755-1315/113/1/012127
彭斯俊, 沈加超, 朱雪. 2014. 基于ARIMA模型的PM2.5预测[J]. 安全与环境工程, (6): 125-128.
Pope Ⅲ C A, Burnett R T, Thun M J. 2002. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution[J]. Journal of the American Medical Association, 287(9): 1132-1141. DOI:10.1001/jama.287.9.1132
Qi Y, Li Q, Karimian H, et al. 2019. A hybrid model for spatiotemporal forecasting of PM2.5 based on Graph Convolutional Neural Network and Long Short-Term Memory[J]. Science of the Total Environment, 664: 1-10. DOI:10.1016/j.scitotenv.2019.01.333
Wang P, Zhang H, Qin Z, et al. 2017. A novel hybrid-Garch model based on ARIMA and SVM for PM2.5 concentrations forecasting[J]. Atmospheric Pollution Research, 8(5): 850-860. DOI:10.1016/j.apr.2017.01.003
夏晓圣, 陈菁菁, 王佳佳, 等. 2020. 基于随机森林模型的中国PM2.5浓度影响因素分析[J]. 环境科学, 5(41): 2057-2065.
薛文博, 韩宝平, 王金南, 等. 2016. PM2.5输送特征与环境容量模拟[M]. 北京: 中国环境出版社.
Yang X, Wu Q, Zhao R, et al. 2019. New method for evaluating winter air quality: PM2.5 assessment using Community Multi-Scale Air Quality Modeling (CMAQ) in Xi'an[J]. Atmospheric Environment, 211: 18-28. DOI:10.1016/j.atmosenv.2019.04.019
Yu R, Yang Y, Yang L, et al. 2016. RAQ-A random forest approach for predicting air quality in urban sensing systems[J]. Sensors, 16(1): 86. DOI:10.3390/s16010086
Zamani Joharestani M, Cao C, Ni X, et al. 2019. PM2.5 prediction based on random forest, XGBoost, and deep learning using multisource remote rensing data[J]. Atmosphere, 10(7): 373. DOI:10.3390/atmos10070373
Zhang D, Bai K, Zhou Y, et al. 2019. Estimating ground-level concentrations of multiple air pollutants and their health impacts in the Huaihe River basin in China[J]. International Journal of Environmental Research and Public Health, 16(4): 579. DOI:10.3390/ijerph16040579
Zhao J, Deng F, Cai Y, et al. 2019. Long Short-Term Memory-Fully connected (LSTM-FC) neural network for PM2.5 concentration prediction[J]. Chemosphere, 220: 486-492. DOI:10.1016/j.chemosphere.2018.12.128