随着城市化和社会经济的高速发展, 我国的大气污染问题日渐突出, 并带来显著的生态环境问题(宋宇等, 2003;Donkelaar et al., 2010; 吴兑等, 2012; Zhang et al., 2012; Guo et al., 2017)和健康影响(Huang et al., 2009; Chen et al., 2010; 胡子梅等2013;Shang et al., 2013; 陶燕等, 2014; Song et al., 2017).为减缓大气污染, 改善环境空气质量, 我国政府相继出台了一系列规划和计划(国务院, 2013; 2016), 大气污染研究和治理工作也取得重要进展(Guo et al., 2014; Wang et al., 2014; Cao et al., 2015; Zhang et al., 2015; Zhou et al., 2017).细颗粒物(PM2.5)是我国最主要的大气污染物之一, 特别是在东部区域(Donkelaar et al., 2010; 张小曳等, 2013; 周广强等2016), 有效的空气质量预报可以帮助政府部门进行空气污染调控决策, 引导公众规避高污染时段, 减小污染暴露和健康风险.
数值模式是开展大气污染研究和空气质量预报的重要工具之一, 在大气环境领域得到了广泛应用(Wang et al., 2014; Zhou et al., 2017; Brasseur et al., 2019; Petersen et al., 2019), 已成为短期空气质量预报的主要手段(Mckeen et al., 2005; Chen et al., 2008; 王茜等2010;Zhou et al., 2017).然而, 由于大气物理过程和化学过程的高度非线性, 气象和空气质量模式还存在诸多不足, 以及人为排放的不确定性和人为源清单时间滞后的影响, 导致环境空气质量数值预报仍然存在不同程度的偏差, 且偏差存在明显的时间和地域差异, 这也与模式使用和污染轻重程度有关.由于气象条件是影响PM2.5等污染物浓度的最主要因素之一(张人禾等, 2014; Chen et al., 2019), 污染物的输送、扩散乃至化学过程都与气象条件密切相关, 并且气象与污染之间的相互反馈(Wang et al., 2014)进一步加剧了气象条件的影响, 因此, 采用不同气象场驱动空气质量模式将引起预报结果出现差异, 从而可以为应用提供不同的选择.从空气质量数值预报的发展过程看, 模式和人为排放清单的不足需要通过长时间的努力逐步改进, 难以在短时间内彻底解决, 这为采用不同气象场驱动模式进行数值预报并开展释用提供了发展和应用空间.
经过多年的发展, 集合或集成技术逐渐成为提升空气质量数值预报效果的重要方法.Monache等(2003)最早将多模式集合方法引入到空气质量的业务预报中, 效果评估结果显示集合预报显著优于单个模式.Brasseur等(2019)和Petersen等(2019)采用中值和均值等方法, 基于中国和欧洲9个业务模式对中国东部城市主要污染物进行了集合预报, 效果评估表明集合预报通常具有最优表现.研究人员针对长三角地区PM2.5也开展了多模式集合或集成预报, 如王茜等(2010)基于NAQPMS、CMAQ、CAMx、WRF-Chem等多个数值模型对上海市的空气质量进行集合预报, 较好地模拟出主要污染物的日变化趋势;瞿元昊等(2018)采用最优集成方法(Optimal Consensus Forecast, 即OCF)对PANDA项目中国和欧洲7个模式预报结果进行集成释用, 显著改善了上海及长三角其他城市PM2.5预报效果.
欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)全球高分辨率数值天气预报以其预报准确性在全球范围内具有重要影响力, 在全球天气预报及相关业务中得到广泛应用, 也是我国天气预报业务的支撑之一.但由于ECMWF高分辨率数值预报数据(ECMWF数据)不免费实时提供, 其很少在区域数值天气预报或环境空气质量数值预报业务中得到应用, 而NCEP GFS(National Centers for Environmental Prediction Global Forecast System)数据因其公开性已成为绝大多数空气质量数值预报的驱动场(如王茜等2015;Zhou et al., 2017).这个现状使得在实际业务应用中, 一旦二者对气象场的预报出现明显分歧, 将困扰预报员使用空气质量数值预报产品.为解决这一问题, 本文研发了采用ECMWF数据驱动的区域环境空气质量数值预报系统, 并结合NCEP GFS数据驱动的数值预报进行集成预报, 以期为空气质量预报和预警业务提供更有力的客观产品支撑.
2 数据与方法(Data and methodology) 2.1 预报系统构建ECMWF数据驱动的区域空气质量预报系统(RAEMS-EC)基于华东区域大气环境数值预报业务系统(RAEMS-GFS)构建.RAEMS-GFS的核心模式为WRF-Chem(Grell et al., 2005), 基础人为源排放清单为清华大学中国多尺度人为排放清单(MEIC, http://www.meicmodel.org/), 详细设置可见文献(Zhou et al., 2017).RAEMS-EC使用与RAEMS-GFS完全相同的模式区域、分辨率、物理化学方案、排放清单及化学边界条件, 二者不同之处在于使用不同的气象初始条件、气象边界条件和化学初始条件.RAEMS-EC气象初始和边界条件使用ECMWF数据, 其水平分辨率为0.125°, 垂直19层(1000、950、925、900、850、800、700、600、500、400、300、250、200、150、100、70、50、20、10 hPa).RAEMS-GFS则使用NCEP GFS全球0.5°分辨率数值预报作为气象初始和边界条件.两个预报系统分别采用各自的前一次24 h预报作为化学初始场.
RAEMS-EC和RAEMS-GFS均每天运行一次, 起报时间为北京时间20:00, 预报时效96 h.气象边界条件每6 h更新一次.RAEMS-EC在2019年9月投入业务应用, 同时由于秋冬季是长三角地区PM2.5的主要污染时段, 本文以2019年秋冬季(2019年11月1日—2020年2月29日, 下同)为研究时间.
2.2 OCF方法OCF是一种最先应用于气象业务预报的数值预报优化方法(Woodcock et al., 2005; 漆梁波等, 2007), 其核心思想体现在滚动检验与加权集成, 影响集成效果的主要因素包括订正因子和集成权重的选择及训练长度.吴剑斌等(2017)在我国东部城市臭氧集成预报时选用四分位数和中位数作为样本进行训练期的订正因子;瞿元昊等(2018)对长三角中心城市PM2.5集成预报时则采用归一化偏差并去除极大和极小值.本文以归一化偏差(NMB)作为订正因子, 以训练期订正后平均预报误差作为集成权重.首先计算模式k在训练期的归一化偏差NMBk(式(1)).进而对模式k在训练期的预报值进行订正(式(2)), 并计算订正后预报值F′k, i的平均误差MEk(式(3)).以MEk的归一化倒数作为权重Wk(式(4)), 这里为2计算得到预报时刻(如预报日)订正后的最优集成预报值FOCF.进行最优集成时每个城市独立计算, 正式集成预报前启动训练以保证集成效果.
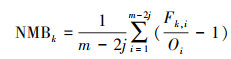
|
(1) |
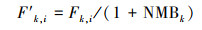
|
(2) |
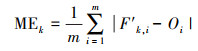
|
(3) |
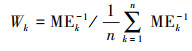
|
(4) |
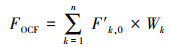
|
(5) |
式中, F表示预报值, O表示观测值, i为自预报时刻后退的时次, m为训练长度, j为成对的极大和极小值去除数, n为模式个数.
2.3 数据与评估方法PM2.5预报效果评估基于城市日平均浓度(日值)进行.观测日值由小时浓度根据国标(GB3095—2012)及其技术规定(HJ633—2012)计算得到, 不考虑对照站点.小时数据来自全国城市空气质量实时发布平台(http://106.37.208.233:20035).共有55个城市的PM2.5日值数据有效率超过75%, 其中, 安徽、江苏、浙江和上海分别有16、24、14和1个;地级以上城市有41个, 县级城市有14个.气象要素评估基于长三角区域238个县级以上气象站数据进行.预报数据采用观测站点所在模式网格的结果, 分析时采用与观测完全相同的计算方法.
预报效果评估时仅使用观测-预报成对数据.PM2.5日值浓度观测数据有效率为99.8%.ECMWF气象场驱动预报数据有效率为95.8%, 观测与预报成对数据有效率为95.7%;GFS驱动预报数据有效率为100%.降水、气温、相对湿度(RH)和风速4个要素的观测数据有效率均在98%以上, 成对数据有效率95%以上.
预报效果评估针对连续量(浓度、温度等)和等级量(PM2.5污染预报)分别进行.连续量评估指标包括相关系数、平均偏差、均方根误差、x(2或1.5)倍比等(周广强等, 2021), 从不同角度描述预报效果.如相关系数可以反映预报与观测在时间变化或空间分布上的一致性程度, 偏差和误差指标可反映预报与观测在数量上的差异, x倍比体现基于记录的预报向观测的集中程度.等级量主要使用TS评分、空报率和漏报率指标, 其分别体现严格意义上污染预报的准确率、误报程度和漏报程度.
3 结果和讨论(Results and discussion) 3.1 近地面气象要素的预报准确性首先分析与PM2.5密切相关的关键近地面气象要素的预报性能.图 1显示了ECMWF气象场驱动的华东区域大气环境数值预报系统对长三角地区238个气象站的站点累积降水、平均2 m温度、平均相对湿度和平均风速的48 h时效(d2)的预报性能.结果表明, 预报对累积降水和平均温度具有非常好的预报效果, 空间相关系数(各站点预报与观测累积或平均值之间的相关系数)均超过0.9, 表明预报与观测在空间分布上非常一致;平均偏差、平均误差及均方根误差与观测值相比均不大;绝大部分数值与观测接近, 约99%在观测的1.5倍与1/1.5(1.5倍比)之间.时间变化趋势上, 小时降水的总体相关系数为0.40(时间相关系数, 样本数超6×105), 小时温度总体相关系数为0.93.平均风速的预报效果总体低于降水和温度, 空间相关系数为0.74, 时间相关系数为0.62, 时空变化趋势与观测具有良好一致性;但存在系统性偏高, 平均偏高1.4 m·s-1, 约为观测均值的2/3, 体现了区域模式对预报风速偏高的基本特征(Chen et al., 2008; Zhou et al., 2017).预报相对湿度的时间变化趋势与观测一致, 总体相关系数达0.72, 但空间一致性较低, 相关系数为0.35;数值上与观测具有良好一致性, 站点平均偏差和误差均在10%以内, 1.5倍比高达1.00.此外, 风向也是影响污染物输送的重要气象要素, 这里定义预报偏差为预报与观测风向的夹角.238个气象站中平均风向预报偏差45°, 各站点平均为24°~88°, 中值为41°, 这与Zhou等(2017)的结果(平均48°, 采用0.5°分辨率GFS气象场驱动)相当.总体上, ECMWF气象场适合作为气象初始条件和边界条件用于开展空气质量数值预报.
 |
| 图 1 ECMWF驱动预报与观测的站点累积降水(a)、平均温度(b)、平均相对湿度(c)和平均风速(d) 对比 Fig. 1 Scatterplot of modeled and observed stational accumulated rain(a), mean temperature(b), mean RH(c) and mean wind speed(d) |
长三角地区55个城市不同预报时效的PM2.5浓度预报效果总体相当(表 1).PM2.5预报浓度随预报时效增加呈弱上升趋势, 其中, 24 h预报与其他3个时效的结果有较大偏离;24 h预报的平均偏差和偏差中值也与其他3个时效有一定的偏离.4个预报时效的FAC2和FAC1.5两个指标则非常接近.96 h预报时效的相关系数较其他时效略小.总的来说, 尽管不同预报时效的效果存在一定的差异, 但差异都不大, 各时效总体上可比, 同时考虑预报业务上的实际应用, 因此, 本文的分析主要基于48 h预报的结果开展.
| 表 1 分时效长三角城市PM2.5浓度预报总体效果 Table 1 General performance statistics of PM2.5 forecast in different prediction length over 55 cities in the YRD region |
ECMWF气象场驱动的数值预报整体上对长三角地区2019年秋冬季的PM2.5浓度具有较好的预报能力(图 2).预报与观测的城市日均PM2.5浓度的总体相关系数为0.6, 均方根误差约为30 μg·m-3;FAC2和FAC1.5分别达到0.76和0.54, 表明预报值多数处于观测值附近.同时也发现预报明显偏高, 以48 h预报为例, 平均偏差为10.7 μg·m-3, 约为观测均值的22%, 其原因可能与疫情期间PM2.5浓度明显下降有关, 如乐旭等(2020)的研究显示, 2020年2—3月期间长三角地区PM2.5浓度较预期下降了16.7 μg·m-3 (34%);平均偏差接近平均误差的1/2, 这表明多数偏差为正偏差;偏差中值为7.9 μg·m-3, 也为明显正值.详细评估指标见表 1.散点分布结果(图 2)显示, 更多点分布于1 ∶ 1线左上侧, 数据点高密度区也主要位于1 ∶ 1和1 ∶ 2线之间, 也反映出PM2.5预报浓度偏高.
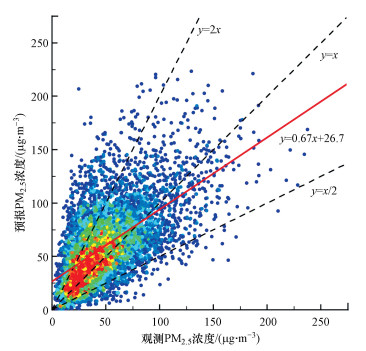 |
| 图 2 观测和预报逐日PM2.5浓度分布对比 (颜色表示数据点密度, 暖色为高) Fig. 2 Scatterplot of observed and forecasted daily PM2.5 concentration (warm colored dots mean higher data density) |
ECMWF气象场驱动预报的长三角地区秋冬季PM2.5浓度分布整体与观测一致(图 3), 呈现“西部和北部高、南部低”的空间分布特征;浓度范围上, 各城市的预报PM2.5浓度基本与观测等级(颜色)相同或相差一个等级内.各城市独立评估结果显示, 55个城市中有22个城市的相关系数超过0.6;17个城市的平均预报偏差绝对值小于5 μg·m-3, 27个城市小于10 μg·m-3;32个城市均方根误差小于30 μg·m-3, 50个城市小于40 μg·m-3;25个城市FAC2超过0.8, 37个城市超过0.7;35个城市FAC1.5超过0.5.因此, 数值预报在大多数城市具有良好表现.
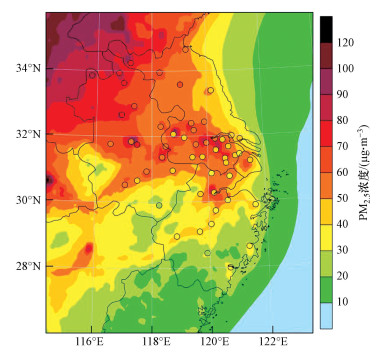 |
| 图 3 观测城市平均(圆圈填充)和预报(阴影)PM2.5浓度分布 Fig. 3 Distribution of city averaged observed (circle filled) and forecasted (shaded) PM2.5 concentration |
RAEMS-EC对长三角城市逐日PM2.5浓度的预报效果整体与RAEMS-GFS预报相当(图 4), 二者之间有非常高的可比性(R2=0.98, 线性斜率1.00);绝大部分数据在1 ∶ 1附近(FAC1.5高达0.99).预报效果的统计指标也都非常接近, 差别非常细微.从图中也可以看出, 有少量RAEMS-EC预报结果在RAEMS-GFS的1.5倍之外, 极个别在1/1.5之外, 体现出一定的差异性, 可以为一些特殊情况提供不同的选择, 也为集成预报提供了基础和必要性.
 |
| 图 4 RAEMS-EC与RAEMS-GFS预报逐日PM2.5浓度分布对比 Fig. 4 Scatterplot of daily PM2.5 concentration forecasted by RAEMS-EC and RAEMS-GFS |
训练长度是OCF方法的重要参数, 其在很大程度上决定了集成预报的效果.本文采用相关系数和均方根误差两个指标来衡量训练长度的影响.图 5显示了不同训练长度下长三角55个城市48 h预报OCF总体效果.从图中可以看出, 随着训练长度的增加, 相关系数在9 d之后达到较高水平, 并呈波动变化趋势, 分别在9、17和25 d处出现峰值, 其中17 d最大;均方根误差呈现先下降后上升的趋势, 在17 d时最小, 变化趋势与吴剑斌等(2017)的结果相似.与此同时, 训练期内计算归一化偏差时极大和极小值的去除也具有明显的影响.除个别情况外, 相关系数随极值去除数的增加一致下降, 均方根误差则一致增加, 因此在本文研究范围内, 以不进行极值去除为宜.与数值预报直接结果相比, 不同训练长度和极值去除数下OCF的预报效果得到明显提升;不去除极值时, OCF的相关系数在7 d时得到改进, 均方根误差在5 d后得到改进, 这也表明RAEMS-EC和RAEMS-GFS对长三角地区PM2.5浓度的预报效果整体稳定, 纳入归一化偏差极值的效果高于其带来的不确定性.总的来说, 采用OCF方法后, 长三角地区的PM2.5浓度预报得到改进, 由此确定训练长度为17 d、不去除极值.
 |
| 图 5 不同训练长度和极端值去除数(图例后数字)下OCF的相关系数(r)和均方根误差(RMSE) Fig. 5 Correlation coefficients (r) and RMSEs of OCF in different training length and number of paired maximal and minimal NMB in training |
采用OCF方法后, PM2.5浓度预报效果相比RAEMS-EC预报显著改进.以48 h为例(表 2), OCF各项指标均得到不同幅度的提升.相关系数从0.60提升至0.72, 提高了0.12, 提升幅度为19%;均方根误差减小8.3 μg·m-3, 下降27%.平均偏差、归一化偏差和偏差中值3个指标提升最为显著, 绝对数值减小约83%;平均误差和误差中值分别下降26%和24%;FAC2和FAC1.5均提高10%以上.从平均偏差(-1.8 μg·m-3)和偏差中值(-1.4 μg·m-3)来看, OCF方法的应用基本解决了数值预报系统性偏高的问题.
| 表 2 长三角城市PM2.5浓度OCF效果及其改进 Table 2 Performance of OCF on PM2.5 concentration and its improvements over YRD cities |
为进一步了解OCF方法的改进效果, 对比分析了OCF和RAEMS-EC预报的长三角城市PM2.5浓度日值偏差分布(图 6).结果显示, RAEMS-EC预报的偏差分布具有较好的对称性, 概率密度集中, ±20 μg·m-3之间占总量的60%, ±10 μg·m-3之间占36%;最大概率密度位于+5 μg·m-3附近, 呈一定的右偏即峰值右侧下降略缓于左侧;正偏差比例为62%, 明显高于负偏差.OCF的预报偏差同样具有良好的对称性且好于RAEMS-EC预报.与数值预报直接结果相比, OCF的峰值更接近0, 位于-2 μg·m-3附近;峰值约0.023 m3·μg-1, 高于RAEMS-EC预报的0.019 m3·μg-1;峰值两侧下降更快, 使得概率分布更向峰值集中, ±20 μg·m-3之间占70%, ±10 μg·m-3之间占44%, 大偏差的比例进一步下降;仍有不足在于, OCF的负偏差(52%)略多于正偏差(46%), 但基本持平.
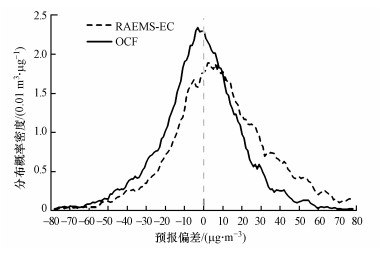 |
| 图 6 预报偏差概率密度分布 Fig. 6 Distribution of probability density function of the forecast biases |
OCF方法的应用使各城市的预报效果也得到了不同程度的提升.如图 7所示, OCF的相关系数和FAC2的城市数向大值区间转移, 即具有更高相关系数和FAC2的城市数显著增加, 尤其是FAC2, 超过0.9的城市占比大于60%;均方根误差则向低值区间移动, 大于30 μg·m-3的城市从23个下降至1个, 大多数城市的均方根误差降至25 μg·m-3以下;平均偏差向小绝对值区间集聚, 绝对值超过5 μg·m-3的城市从42个下降至3个.其他指标也有显著提升(表 2), 除平均偏差(84%)和FAC1.5(89%)外, 均在90%以上城市得到提升;这个结果也表明, OCF造成在个别城市的个别指标下降, 针对这些城市需要更详细的分析或采用其他方法进行订正.
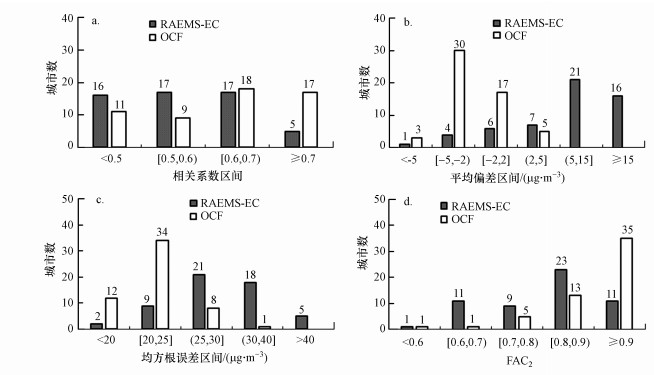 |
| 图 7 不同评估指标区间内的城市数 (a~d分别为相关系数、平均偏差、均方根误差和FAC2) Fig. 7 Number of city for different evaluation indices (a~d represents r, MB, RMSE and FAC2, respectively) |
对污染的预报能力是空气质量预报中的重要指标之一.研究时段内, 长三角城市的PM2.5污染率为17.2%, 其中, 中度以上污染率为4.2%, 重度以上污染率为1.0%, 总的来说污染发生率比较低, 因此, 本文讨论污染预报效果, 不区分等级.采用OCF方法后(表 3), 长三角城市PM2.5污染预报的TS评分从RAEMS-EC的0.35提升至0.40, 增加了14%, 预报水平明显提升;空报率从0.58下降至0.38, 但漏报率有所上升, 从0.34增至0.46.空报率和漏报率的改变主要来源于PM2.5预报浓度的总体下降.
| 表 3 PM2.5污染预报效果对比 Table 3 Forecast performance for PM2.5 pollution |
1) 本文建立了使用欧洲中期天气预报中心全球高分辨率数值天气预报数据、基于华东区域大气环境数值预报业务系统(RAEMS-GFS)框架的区域空气质量数值预报系统(RAEMS-EC).RAEMS-EC除气象初始条件、边界条件和化学初始条件外采用与RAEMS-GFS完全相同网格、物理化学方案等设置和人为源排放清单.RAEMS-EC的建立为区域空气质量预报和空气污染预警提供了新的客观预报支撑.
2) RAEMS-EC于2019年9月投入业务应用, 其对2019年秋冬季长三角地区与空气质量密切相关的气象要素和PM2.5浓度均有良好的预报效果.不同时效的预报具有良好的一致性, 长三角55个城市PM2.5浓度预报效果总体相当;较好地预报了长三角地区PM2.5的空间分布和时间变化;各城市评估结果显示, 在大多数城市具有良好表现.与此同时, 数值上存在一定的偏高, 平均偏高约10 μg·m-3.RAEMS-EC与RAEMS-GFS预报在具有高度可比性的同时也存在一定的差异.
3) RAEMS-EC与RAEMS-GFS最优集成预报可以大幅提升长三角地区PM2.5的预报效果.训练长度17 d、不去除极值是合适的OCF参数, 其结果同时具有最高的相关系数和最小的均方根误差.OCF的应用使得预报偏差显著改善, 预报偏差分布显著向零值集中;相关系数明显提升, 预报误差明显下降, 2个倍比指标均升高12%.各城市的预报效果也得到不同程度的提升, 相关系数大于0.7的城市数明显增多, 均方根误差大于25 μg·m-3的城市数明显减少, 绝大部分城市的评估指标明显上升;反映污染预报能力的TS评分也有明显提升.OCF基本解决了数值预报系统偏高的不足, 可以显著提升空气质量数值预报的业务应用能力和效果.
Brasseur G, Xie Y, Petersen A, et al. 2019. Ensemble forecasts of air quality in eastern China-part 1:model description and implementation of the MarcoPolo-Panda prediction system, version 1[J]. Geoscientific Model Development, 12: 33-67. DOI:10.5194/gmd-12-33-2019 |
Cao Z, Sheng L, Liu Q, et al. 2015. Interannual increase of regional haze-fog in North China Plain in summer by intensified easterly winds and orographic forcing[J]. Atmospheric Environment, 122: 154-162. DOI:10.1016/j.atmosenv.2015.09.042 |
Chen J, Vaughan J, Avise J, et al. 2008. Enhancement and evaluation of the AIRPACT ozone and PM2.5 forecast system for the Pacific Northwest[J]. J.Journal of Geophysical Research-Atmosphere, 113(D14): 762-770. |
Chen L, Zhu J, Liao H, et al. 2019. Assessing the formation and evolution mechanisms of severe haze pollution in the Beijing-Tianjin-Hebei region using process analysis[J]. Atmospheric Chemistry and Physics, 19: 10845-10864. DOI:10.5194/acp-19-10845-2019 |
Chen R, Chen C, Tan J, et al. 2010. Ambient air pollution and hospital admission in Shanghai, China[J]. Journal of Hazardous Materials, 181(1/3): 234-240. |
Donkelaar A, Martin R, Brauer M, et al. 2010. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: development and application[J]. Environmental Health Perspectives, 118(6): 847-855. DOI:10.1289/ehp.0901623 |
Grell G, Peckham S, Schmitz R, et al. 2005. Fully coupled "online" chemistry within the WRF model[J]. Atmospheric Environment, 39: 6957-6975. DOI:10.1016/j.atmosenv.2005.04.027 |
Guo S, Hu M, Zamora M, et al. 2014. Elucidating severe urban haze formation in China[J]. Proceedings of the National Academy of Sciences of the United States of America, 111: 17373-17378. DOI:10.1073/pnas.1419604111 |
Guo H, Cheng T, Gu X, et al. 2017. Assessment of PM2.5 concentrations and exposure throughout China using ground observations[J]. Science of the Total Environment, 601-602: 1024-1030. DOI:10.1016/j.scitotenv.2017.05.263 |
国务院. 2016. "十三五"生态环境保护规划(国发[2016]65号)[OL]. 2020-08-13. http://www.gov.cn/zhengce/content/2016-12/05/content_5143290.htm
|
国务院. 2013. 大气污染防治行动计划(国发[2013]37号)[OL]. 2020-08-13. http://www.gov.cn/zwgk/2013-09/12/content_2486773.htm
|
胡子梅, 王军, 陶征楷, 等. 2013. 上海市PM2.5重金属污染水平与健康风险评价[J]. 环境科学学报, 33(12): 3399-3406. |
Huang W, Tan J, Kan H, et al. 2009. Visibility, air quality and daily mortality in shanghai, China[J]. Science of the Total Environment, 407(10): 3295-300. DOI:10.1016/j.scitotenv.2009.02.019 |
Mckeen S, Wilczak J, Grell G, et al. 2005. Assessment of an ensemble of seven real-time ozone forecasts over Eastern North America during the summer of 2004[J]. Journal of Geophysical Research-Atmosphere, 112: 3003-3013. |
Monache L, Stull R. 2003. An ensemble air-quality forecast over western Europe during an ozone episode[J]. Atmospheric Environment, 37(25): 3469-3474. DOI:10.1016/S1352-2310(03)00475-8 |
Petersen A, Brasseur G, Bouarar I, et al. 2019. Ensemble forecasts of air quality in eastern China-Part 2:Evaluation of the MarcoPolo-Panda prediction system, version 1[J]. Geoscientific Model Development, 12: 1241-1266. DOI:10.5194/gmd-12-1241-2019 |
漆梁波, 曹晓岗, 夏立, 等. 2007. 上海区域要素客观预报方法效果检验[J]. 气象, 33(9): 9-18. DOI:10.3969/j.issn.1000-0526.2007.09.002 |
瞿元昊, 许建明, Brasseur G, 等. 2018. 利用多模式最优集成方法预报上海PM2.5[J]. 环境科学学报, 38(9): 3449-3456. |
Shang Y, Sun Z, Cao J, et al. 2013. Systematic review of Chinese studies of short-term exposure to air pollution and daily mortality[J]. Environment International, 54: 100-111. DOI:10.1016/j.envint.2013.01.010 |
Song C, He J, Wu L, et al. 2017. Health burden attributable to ambient PM2.5 in China[J]. Environmental Pollution, 223: 575-586. DOI:10.1016/j.envpol.2017.01.060 |
宋宇, 唐孝炎, 方晨, 等. 2003. 北京市能见度下降与颗粒物污染的关系[J]. 环境科学学报, 23(4): 468-471. |
陶燕, 刘亚梦, 米生权, 等. 2014. 大气细颗粒物的污染特征及对人体健康的影响[J]. 环境科学学报, 34(3): 592-597. |
Wang Z, Li J, Wang Z, et al. 2014. Modeling study of regional severe hazes over mid-eastern china in January 2013 and its implications on pollution prevention and control[J]. Science China-Earth Science, 57(1): 3-13. DOI:10.1007/s11430-013-4793-0 |
王茜, 伏晴艳, 王自发, 等. 2010. 集合数值预报系统在上海市空气质量预测预报中的应用研究[J]. 环境监控与预警, 2(4): 1-6. DOI:10.3969/j.issn.1674-6732.2010.04.001 |
王茜, 吴剑斌, 林燕芬. 2015. CMAQ模式及其修正技术在上海市PM2.5预报中的应用检验[J]. 环境科学学报, 35(6): 1651-1656. |
Woodcock F, Engel C. 2005. Operational consensus forecasts[J]. Weather and Forecasting, 20(1): 101-111. DOI:10.1175/WAF-831.1 |
吴兑, 刘啟汉, 梁延刚, 等. 2012. 粤港细粒子(PM2.5)污染导致能见度下降与灰霾天气形成的研究[J]. 环境科学学报, 32(11): 2660-2669. |
吴剑斌, 肖林鸿, 晏平仲, 等. 2017. 最优化集成方法在城市臭氧数值预报中的应用研究[J]. 中国环境监测, 33(4): 213-220. |
乐旭, 雷亚栋, 周浩, 刘竹, 等. 2020. 新冠肺炎疫情期间中国人为碳排放和大气污染物的变化[J]. 大气科学学报, 43(2): 265-274. |
Zhang X, Wang Y, Niu T, et al. 2012. Atmospheric aerosol compositions in China: Spatial/temporal variability, chemical signature, regional haze distribution and comparisons with global aerosols[J]. Atmospheric Chemistry and Physics, 11: 26571-26615. |
Zhang B, Wang Y, Hao J. 2015. Simulating aerosol-radiation-cloud feedbacks on meteorology and air quality over eastern China under severe haze conditions in winter[J]. Atmospheric Chemistry and Physics, 15: 2387-2404. DOI:10.5194/acp-15-2387-2015 |
张人禾, 李强, 张若楠. 2014. 2013年1月中国东部持续性强雾霾天气产生的气象条件分析[J]. 中国科学: 地球科学, 44(1): 27-36. |
张小曳, 孙俊英, 王亚强, 等. 2013. 我国雾-霾成因及其治理的思考[J]. 科学通报, 13(13): 1178-1187. |
Zhou G, Xu J, Xie Y, et al. 2017. Numerical air quality forecasting over eastern China: an operational application of WRF-Chem[J]. Atmospheric Environmental, 153: 94-108. DOI:10.1016/j.atmosenv.2017.01.020 |
周广强, 瞿元昊, 余钟奇. 2021. 长三角城市臭氧数值预报与释用[J]. 中国环境科学, 41(1): 28-36. DOI:10.3969/j.issn.1000-6923.2021.01.004 |
周广强, 谢英, 吴剑斌, 等. 2016. 基于WRF-Chem模式的华东区域PM2.5预报及偏差原因[J]. 中国环境科学, 36(8): 2251-2259. DOI:10.3969/j.issn.1000-6923.2016.08.002 |
 2021, Vol. 41
2021, Vol. 41


