2. 德克萨斯大学里奥格兰德河谷分校, 爱丁堡 78539;
3. 昆明理工大学冶金节能减排教育部工程研究中心, 昆明 650093;
4. 昆明理工大学冶金与能源工程学院, 昆明 650093
2. College of Business & Entrepreneurship, University of Texas Rio Grande Valley, Edinburg 78539;
3. Engineering Research Center of Metallurgical Energy Conservation and Emission Reduction, Ministry of Education, Kunming 650093;
4. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming 650093
我国改革开放之初, 以粗放型增长方式推进工业化、城市化, 城市规模、能源消耗等快速增加, 大气污染问题也在迅速地恶化, 造成了近年来的空气质量问题(Song et al., 2017; 赵秀玲等, 2020).根据《2019中国生态环境状况公报》(生态环境部, 2019), 2019年全国空气质量符合标准的只有157个城市, 占46.6%.准确可靠的预测模型可以提供的大气污染物发展情况, 使公众能及时规避健康风险.此外, 其提供的大气污染物浓度变化的详细信息, 可为环境保护部门提供直观的量化参考, 益于动态调整大气污染防治计划.《上海市清洁空气行动计划(2018—2022年)》中指出, 要进一步加强长三角地区空气质量预报中心能力建设, 要加大空气质量和气象预报预警技术的科研力度.然而, 大气环境本质上是一个动态、非线性、非平稳、有噪声的系统, 使得其变化规律被隐藏, 难以被精准预测(Kurt et al., 2010).因此, 如何深入挖掘并提取大气污染物浓度序列中蕴含的规律, 对大气污染物在未来一段时期的变化趋势进行准确预测, 成为亟待解决的难题.
大气环境污染物的预测值作为制定和动态调整防治措施的重要参考, 对其精度的要求在不断提高.目前, 针对大气环境污染物浓度的预测方法主要有统计模型、灰色理论、数值模型和神经网络模型.统计模型常见的有移动平均自回归模型(ARIMA)和回归模型等, 例如, 孟凡强(2009)使用ARIMA模型对空气质量进行预测; 付倩娆(2016)使用多元回归方法对雾霾进行预测研究.统计模型通常要求数据具有正态分布或平稳等特性, 不适宜直接用于污染物浓度预测.灰色预测模型是灰色系统理论的一部分, 常用于贫信息、小样本的预测(Deng, 2017).Pao等(2012)、Wu和Zhao(2019)都应用灰色预测技术解决大气领域预测问题.但灰色模型受波动影响较大, 且预测精度随着样本量的增大而降低.因此, 对于中等样本量的月均浓度数据预测精度较低.数值模型是以空气动力学为理论基础建立空气污染物的变化和扩散模型, 主要是通过计算机来模拟空气污染物在大气中动态演变过程, 以实现模拟和预测空气污染物浓度在大气中的分布和发展(聂邦胜等, 2008).目前国内外常用的区域尺度数值模型主要有: CMAQ(Wang et al., 2017)、CAMx(沈劲等, 2011)、WRF-Chem(周广强等, 2017)和我国自主研发的嵌套网格空气质量预报模式系统(王自发等, 2006).数值模型可以模拟地区的污染物发展状况和对空气质量情况进行预报, 由于计算量庞大, 缺乏时效性, 不适用于月均浓度的预测工作.神经网络模型因具有模拟人脑的学习和记忆的能力, 能够学习历史数据中的线性和非线性信息, 在污染物预测领域有广泛应用, 如孙宝磊(2017)使用反向传播神经网络实现了大气污染浓度预测.梁泽等(2020)使用径向基神经网络(RBF-NN)对PM2.5进行预测.然而神经网络模型需要大样本进行训练才能得到理想的预测精度, 当用于月均浓度预测时, 由于缺乏充分的训练, 预测精度较低.
单一模型在处理大气环境污染物月均浓度时间序列时往往存在一定的不足, 预测精度无法满足需要.为此, 有学者尝试使用组合预测模型对大气环境污染物, 通过将多个模型巧妙结合在一起, 取长补短, 以解决单一模型存在的缺陷.常见的组合模型常采用以下3种模式: 残余处理模式、权重组合模式和数据分解模式.宋国君等(2018)采用残余处理模式, 使用支持向量机对ARIMA预测结果的残余进行处理, 得到较高精度的PM2.5预测结果.残余处理模式没有改变单一模型的适用范围, 因此在处理高噪音、非平稳和非线性系统时具有很大的局限性.Song和Fu(2020)采用权重组合模式, 分别使用3种子模型对空气质量序列进行预测, 最后对3组预测结果加权求和得到高精度的预测结果.权重组合模式下, 仅当子模型预测结果的残余能够刚好抵消时才能得到理想的精度.因此, 预测精度受子预测模型和权重分配方法的约束, 一种权重组合式的模型往往仅适用某一特定变化的数据.不同因素对污染物浓度变化影响频率不同, 如气温、风速等气象要素往往造成浓度的短时变化, 而政策约束往往反映在长期变化中.各种因素造成不同频率的影响使得月均浓度数据变化复杂, 是造成其难以被预测的主要因素之一.由于分解模型可将原始时间序列数据分解为多个不同频率的子序列, 使得数据包含的不同频率的规律信息能够充分被识别、分离和提取, 被广泛应用到大气环境污染物浓度的预测工作.例如, 郑霞等(2020)基于数据分解模式将小波分解算法和支持向量机算法结合, 构建大气污染物浓度预测模型.秦喜文等(2016)采用整体经验模态分解和支持向量回归对北京日均PM2.5进行预测.
综上所述, 采用数据分解模式的组合模型在大气领域的预测方向已取得了一定的成果, 但由于大多现存的模型都直接采用机器学习技术对子序列进行预测, 导致提出组合预测模型往往针对大样本量的日均数据, 不适用于政策参考所需的月均数据.此外, 受数据采集过程中人为测量误差、仪器仪表精度和有效数字选取的影响, 月均浓度统计数据往往在某种程度上偏离真实浓度数据, 该差距被称为噪音.预测工作中, 月均浓度数据中的高噪音会对预测精度造成消极的影响, 而现有研究大多忽略了对噪音的有效处理.因此, 本文从大气环境污染物月均浓度序列本身出发, 针对空气污染物月均浓度, 将分解技术与时间序列预测技术、神经网络技术相结合, 提出一种适用于高噪音、非平稳和非线性系统的月均浓度组合预测模型.模型使用时间序列预测和灰色预测模型替代常用的机器学习技术, 实现组合模型对中等规模数据的高精度预测, 并进一步考虑数据噪音的影响, 在分解过程中实现降噪.为实现预测精度的进一步提升, 将神经网络技术引入重构过程, 取代传统的求和算法, 实现对子序列预测结果的优化.将所提出的模型用于上海市3种主要大气环境污染物月均浓度(PM2.5、SO2和NO2)预测, 并分别与RBF-NN、CEEMDAN-ARIMA-GM(1, 1)模型和CEEMDAN-ARIMA-GM(1, 1)-Elman模型进行对比分析, 以验证该模型的有效性.
2 建模方法(Modeling methods) 2.1 CEEMDAN分解模型EMD模型是由Huang等(1998)提出的一种将非平稳信号处理为变化频率不同且相对平稳的本征模态函数(IMF)和残余项的方法.它的基本思想是: 先通过原始时间序列数据局部极值构造上、下包络线, 然后根据包络线不断提取在不同频率下的IMF, 直到剩下满足要求的残余项.由于数据中蕴含着大量噪音, 导致传统EMD模型的分解效果不好, 经常出现一个模态中产生尺度不同的振荡, 或者在不同模态中产生尺度相近的振荡, 即模态混叠.为解决这一问题, 学者们相继提出了集成经验模态分解(Wu et al., 2009)、完整集成经验模态分解(Yeh et al., 2010)和具有自适应噪声的完整集成经验模态分解(CEEMDAN)(Torres et al., 2011)等.其中CEEMDAN通过自适应增加和消除白噪声, 削弱了模态混叠现象, 同时降低了重构误差, 对非平稳信号具有较好的分解性能.具体的建模过程如下:
设有一组大气环境污染物浓度时间序列x(n), n=1, 2, …, N代表样本量.定义算子Ek(·)是使用传统EMD方法分解所得到的第k阶IMF.
(1) 对大气环境污染物浓度序列添加噪音.生成一组具有标准正态分布的白噪音序列w(i)(n), I>1, 其中I代表试验组数.将生成的白噪音添加到原始序列中, 得到I组初始数据:
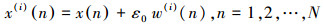
|
(1) |
(2) 对每组初始数据进行EMD分解, 对所有组的第一阶IMF取平均, 得到第一个子序列.

|
(2) |
此时, 第一阶段剩余分量为:
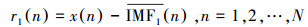
|
(3) |
(3) 继续对于第t阶段剩余分量进行分解, 得到第t阶IMF:
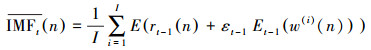
|
(4) |
此时, 第t阶段剩余分量为:
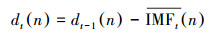
|
(5) |
(4) 重复步骤(3)直到剩余分量满足终止规则

|
(6) |
此时, 剩余分量为残余项R(n).
需要注意的是, 一个剩余分量被定义为IMF需满足以下两个条件: 极值(极大值和极小值)的数目和过零点的次数必须等于或最多相差1;上下包络线的均值必须为零.若不满足任一条件, 该剩余分量需要被进一步分解, 直到满足条件.
2.2 ARIMA预测模型ARIMA模型是由Box和Jenkins提出的一种经典的时间序列预测方法.它假设序列的当前值与其历史有关, 可以表示为历史的组合.ARIMA可以理解为由3个部分组成: 差分阶数, 自回归模型(AR)和移动平均模型(MA), 可表示为式(7).
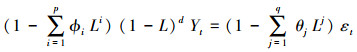
|
(7) |
式中, p为自回归阶数, d为差分阶数, q为移动平均阶数, L为滞后算子, ϕ为自回归部分的系数, θ为移动平均部分的系数, ε为一个白噪声序列.
具体的建模过程如下:
(1) 对IMF进行平稳性检验, 若序列为非平稳, 则使用差分法使其平稳, 差分阶数为d.
(2) 根据IMF自相关和偏自相关图大致判断模型参数范围, 并根据赤池信息准则(AIC)和贝叶斯信息准则(BIC)准则, 确定参数p和q.
(3) 对建立的模型进行评价, 若残差满足白噪音特征, 则说明该模型合适, 否则需要重新建立模型.
2.3 GM(1, 1)预测模型灰色预测模型主要原理是通过累积生成算子(AGO)来增强数据规则, 从而提取出数据中隐藏的信息, 其优点是利用小样本可以做出更准确的预测.GM(1, 1)模型具体的建模过程如下:
设非负序列X(0)(m)={x(0)(1), x(0)(2), …, x(0)(m)}, m=1, 2, …, M为样本量.
(1) 对X(0)进行一阶累加, 生成新序列:
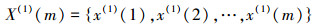
|
(8) |
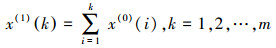
|
(9) |
(2) 构建灰微分方程:

|
(10) |
其中, a为发展系数, b为灰作用量, z(1)(k)是背景公式, 定义为式(11).

|
(11) |
(3) 使用最小二乘法估计参数a和b.

|
(12) |
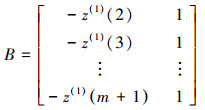
|
(13) |
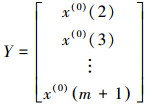
|
(14) |
(4) 将估计参数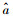
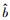
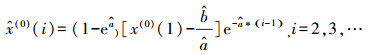
|
(15) |
由于GM(1, 1)的预测精度随着样本量的增加而降低, 本文对GM(1, 1)模型添加滚动机制, 即6个样本为一组, 滚动进行预测.
2.4 RBF神经网络模型RBF-NN是一种前馈神经网络方法, 它的信息沿着一个方向从输入层传递到输出层.RBF-NN的结构(输入层、隐含层和输出层)比其他神经网络方法简单, 仅为三层, 因此其学习收敛速度快, 可以逼近任意非线性函数, 具有很强的非线性拟合能力.在RBF-NN中, 输入层为归一化数据; 隐含层只有一个, 由多个神经元组成; 输出层是隐含层中每个神经元输出的线性加权和.RBF-NN可以表示为式(16).
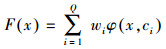
|
(16) |
其中, Q为隐含层神经元的数量, wi为第i个神经元对应的权重值, ci为第i个神经元的中心, φ(·)为径向基函数, 可表示为式(17).
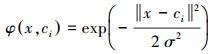
|
(17) |
式中, σ为基函数的作用宽度.
3 组合预测模型的构建及评价指标(Modeling of hybrid prediction framework and evaluation indices) 3.1 模型的建模思想及建模过程CEEMDAN-ARIMA-GM(1, 1)-RBFNN模型采用数据分解模式, 其思路为: 首先, 利用CEEMDAN模型对时间序列进行分解处理, 得到若干不同频率的IMF和残余项, 由于基于EMD的模型的一个优点在于它不仅可以分解出不同频率的子序列, 还可以分离噪音(Nazir et al., 2019).因此, 本文将最高频的IMF1移除, 实现降噪过程; 其次, 对剩余有规律IMF建立ARIMA模型进行预测, 对残余项建立带滚动机制的GM(1, 1)模型进行预测, 实现子序列预测过程; 最后, 将子序列的预测结果输入RBF-NN得到最终预测结果, 实现重构过程.流程图如图 1所示.
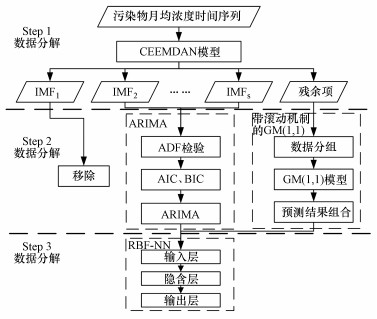 |
| 图 1 CEEMDAN-ARIMA-GM(1, 1)-RBFNN预测模型流程 Fig. 1 The flow chart of CEEMDAN-ARIMA-GM(1, 1)-RBFNN model |
具体步骤如下:
(1) 将大气环境污染物浓度序列输入到CEEMDAN模型, 分解得到若干不同频率的IMF和一组残余项, 移除频率最高的IMF分量.
(2) 对IMF分量做平稳性检验, 若不平稳, 使用差分法处理为平稳, 随后根据AIC和BIC准则, 建立ARIMA模型对IMF进行滚动预测.
(3) 重复步骤(2), 得到所有剩余IMF的预测结果.
(4) 建立GM(1, 1)模型对残余项进行滚动预测.
(5) 使用RBF-NN模型对子序列的预测结果进行重构, 得到大气环境污染物浓度的最终预测结果.
关键参数设定: 在进行CEEMDAN分解时需添加白噪音以缓解模态混叠现象, 添加白噪音的试验组数会影响到最终的分解结果, 为得到较为稳定的结果, 试验组数I选择为500;在对IMF进行平稳性检验时, 本文采用的单位根检验方法为常用的ADF(Augmented Dickey-Fuller)检验方法; 由于研究对象的样本量较长, 而GM(1, 1)的预测精度会随着样本量的增加而降低(Wu et al., 2013), 因此本文在使用GM(1, 1)对残余项进行预测时, 采用滚动预测的方式, 即先将数据分组, 单组样本量为6个样本(GM(1, 1)最佳适用规模), 第一组为前6个样本, 第二组为第2~7个样本, 依此类推, 对每个分组进行预测, 将各组的预测结果进行结合得到所需预测结果.
3.2 评价指标为定量地评价模型的性能, 选取绝对百分比误差(APE)、平均绝对百分比误差(MAPE)、均方误差(RMSE)和皮尔逊相关系数(PCC)4个指标.其中, APE表征单个预测结果的误差, 用于评价模型对未来值的预测性能; MAPE表征多个预测结果的平均误差, 用于评价模型对于现有数据的拟合性能; RMSE同样是反映多个预测值误差的情况的一种方法, 但其可以体现误差的离散程度, 该数值越小一定程度上反映误差波动较小; PCC表征预测结果与实际数据的相关性, 该数值越接近于1表明模型对现有数据拟合状况越好.4种指标计算公式分别见式(18)~(21).
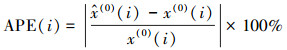
|
(18) |
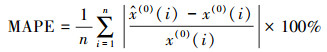
|
(19) |
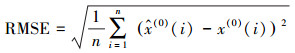
|
(20) |
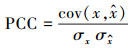
|
(21) |
数据来源于上海市生态环境局大气环境质量月报, https://sthj.sh.gov.cn/hbzhywpt1143/hbzhywpt5156/index.html. 选取月报中公开的上海市3种主要大气环境污染物(PM2.5、SO2和NO2)月均浓度序列为研究对象, 截取2017年1月—2020年7月的统计数据, 即每种污染物43个有效样本数据, 共3组.原始数据如图 2所示, 基本统计特征如表 1所示.
 |
| 图 2 2017年1月—2020年7月上海市PM2.5、SO2和NO2月均浓度 Fig. 2 The monthly mean concentration of PM2.5、SO2 and NO2 in Shanghai from January 2017 to August 2020 |
| 表 1 上海市PM2.5、SO2和NO2月均浓度基本统计特征 Table 1 Basic statistical characteristics of monthly mean concentration of PM2.5、SO2 and NO2 in Shanghai |
由图 2可知, PM2.5和NO2具有相似的数据特征, 月波动较为剧烈, 年变化呈“V”型, 冬季月均浓度高, 夏季的月均浓度较低.而SO2的变化较为平缓, 波动幅度较小, 季节特征不明显.
由表 1可知, 3组样本数据中, PM2.5和NO2属于同一量级, 而SO2量级相对较小, 其均值仅为8.89 μg · m-3, 且呈现较为明显下降趋势.为进一步分析样本数据的平稳性特征, 对3组样本数据进行ADF检验, 结果表明在显著性水平为95%时, SO2和NO2月均浓度序列是非平稳序列.综上所述, 3组样本数据具有不同的数据特征, 可以充分验证组合预测模型的预测性能.
4.2 预测结果分析选取上海市3种大气环境污染物(PM2.5、SO2和NO2)月均浓度, 共43个有效样本为研究对象, 其中前42个样本(2017年1月—2020年6月)用于构建模型, 最后1个样本(2020年7月)用于检测模型的预测性能, 为保证对样本量受限数据的信息进行充分的提取与学习, 子模型(RBF-NN)采用留一法训练.使用CEEMDAN模型对三组原始序列前42个样本进行分解, 结果如图 3所示; 将最高频IMF移除, 对剩余子序列使用ARIMA和带滚动机制的GM(1, 1)模型进行预测; 最后, 使用RBF-NN模型对子序列的预测结果进行优化, 重构得到最终预测结果, 如图 4所示.
 |
| 图 3 上海市PM2.5、SO2和NO2月均浓度的CEEMDAN分解结果 Fig. 3 The decomposition results of monthly mean concentration of PM2.5、SO2 and NO2 in Shanghai |
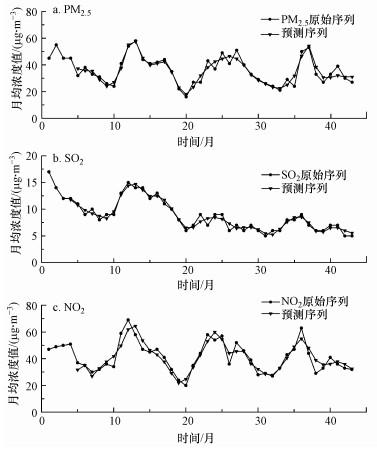 |
| 图 4 CEEMDAN-ARIMA-GM(1, 1)-RBFNN预测结果 Fig. 4 The prediction results of CEEMDAN-ARIMA-GM(1, 1)- RBFNN |
由图 3可知, CEEMDAN将PM2.5、SO2和NO2月均浓度序列分别分解为4个、5个、4个子序列.3组的子序列中, IMF的变化频率都依次降低, 其中IMF1变化频率最快且无序, 其余IMF的变化具有明显的周期性.为进一步验证IMF1近似为噪音的合理性, 对其使用随机性检验.经游程检验, 3个实例中的IMF1均为被判定为随机序列, 可被近似为噪音.
从图 4中可以直观地看到CEEMDAN-ARIMA-GM(1, 1)-RBFNN模型的预测序列与原始序列近乎重叠, 实现了对原始序列的较好拟合, 这充分说明模型能够深入挖掘具有非平稳和非线性特征的原始序列的变化规律, 并进行很好的学习, 实现高精度的预测.此外, 未出现明显的受噪音波动影响而造成的偏移, 表明模型具有较好的抗噪能力.
4.3 对比分析为探究数据模式下组合预测模型的优越性及神经网络模型在组合模型中的作用, 选取RBF-NN、CEEMDAN-ARIMA-GM(1, 1)、CEEMDAN-ARIMA-GM(1, 1)-Elman进行对比研究.使用上述4种模型对相同的样本(上海市PM2.5、SO2和NO2月均浓度数据)进行预测, 2017年1月—2020年6月月均浓度数据用于构建模型, 2020年7月月均浓度数据用于检测模型的预测性能, 结果如表 2所示.
| 表 2 上海市PM2.5、SO2和NO2预测结果及评价指标 Table 2 The prediction results and evaluation indices of PM2.5、SO2 and NO2 in Shanghai |
由表 2可知: (1)对于CEEMDAN-ARIMA-GM(1, 1)-RBFNN模型, 根据预测结果和APE, 3组实例的平均预测误差仅为10%左右; 根据MAPE和RMSE, 模型对于历史数据的拟合误差均在10%以内, 且稳定; 根据PCC, 3组实例的PCC指标均大于0.9, 即预测序列与原始序列具有强相关关系, 反映了模型的优越性能.
(2) 将RBF-NN模型与其他3种模型作对比, 3个实例的评价指标均显示, RBF-NN模型的预测性能最低.尤其是对PM2.5和NO2进行预测时, PCC仅为0.6左右, 仅为中等程度相关.这一结果说明, 当对年度或月度数据(样本量较小)进行预测时, 神经网络模型没有充分的样本进行训练, 导致预测性能较低, 不适用于对空气污染物的月均浓度预测.
(3) 使用RBF-NN模型进行子序列预测结果重构的组合预测模型的APE、MAPE和RMSE分别比使用求和算法重构的组合模型的平均降低了46.95%、19.46%和16.40%.而Elman模型分别降低了22.52%、12.06%和8.79%.这表明使用神经网络算法对结果进行优化的组合模型比采用传统求和算法重构的组合预测模型具有更好的预测性能.
(4) 对比CEEMDAN-ARIMA-GM(1, 1)-RBFNN和CEEMDAN-ARIMA-GM(1, 1)-Elman, 在PM2.5实例中, 使用Elman的组合模型的预测性能比使用RBF-NN的组合模型优1%左右, 而在NO2实例中, 使用RBF-NN的组合模型的预测性能比使用Elman的组合模型优18%左右.这说明Elman模型对结果的优化性能不稳定, 而RBF-NN模型对低维且样本量较小的非平稳、非线性的系统优化性能更强, 更适用于样本量较小的月均浓度序列预测.
5 结论(Conclusions)1) 针对高噪音、非平稳和非线性系统中样本量受限的大气污染物月均浓度序列, 本文构建的CEEMDAN-ARIMA-GM(1, 1)-RBFNN模型预测性能较好, 平均预测误差仅为10%左右.
2) 将提出的组合模型分别与RBF-NN、CEEMDAN-ARIMA-GM(1, 1)模型和CEEMDAN-ARIMA-GM(1, 1)-Elman模型进行对比, 所提出模型的APE、MAPE、RMSE和PCC 4个指标的平均值分别为9.05、8.72、2.92和0.94, 其预测性能比其他3种模型优越.
3) 通过对比分析得知, 对于大气污染物浓度的月均浓度数据, 采用分解模式的组合模型相较于神经网络模型预测性能优越; 使用神经网络模型对结果进行重构能够提高组合模型的预测精度, 且在样本量相对较小的情况下, RBF-NN对预测结果的优化性能更好, 比Elman多提升约25%的性能.
Deng J L. 1982. Control problems of grey systems[J]. Systems & Control Letters, 1(5): 288-294. |
付倩娆. 2016. 基于多元线性回归的雾霾预测方法研究[J]. 计算机科学, 43(Z6): 526-528. |
Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
Kurt A, Oktay A B. 2010. Forecasting air pollutant indicator levels with geographic models 3days in advance using neural networks[J]. Expert Systems with Applications, 37(12): 7986-7992. DOI:10.1016/j.eswa.2010.05.093 |
梁泽, 王玥瑶, 岳远紊, 等. 2020. 耦合遗传算法与RBF神经网络的PM2.5浓度预测模型[J]. 中国环境科学, 40(2): 523-529. DOI:10.3969/j.issn.1000-6923.2020.02.007 |
孟凡强. 2009. ARIMA模型在空气污染指数预测中的应用[J]. 统计与决策, 7: 33-35. |
聂邦胜. 2008. 国内外常用的空气质量模式介绍[J]. 环境科技, 27(1): 125-128. |
Nazir H M, Hussain I, Ahmad I, et al. 2019. An improved framework to predict river flow time series data[J]. PeerJ, 7: 1-22. |
Pao H T, Fu H C, Tseng C L. 2012. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model[J]. Energy, 40: 400-409. DOI:10.1016/j.energy.2012.01.037 |
秦喜文, 刘媛媛, 王新民, 等. 2016. 基于整体经验模态分解和支持向量回归的北京市PM2.5预测[J]. 吉林大学学报(地球科学版), 46(2): 563-568. |
生态环境部. 2019. 2019中国生态环境状况公报[R]. 北京: 生态环境部
|
孙宝磊, 孙暠, 张朝能, 等. 2017. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 37(5): 1864-1871. |
宋国君, 国潇丹, 杨啸, 等. 2018. 沈阳市PM2.5浓度ARIMA-SVM组合预测研究[J]. 中国环境科学, 38(11): 4031-4039. DOI:10.3969/j.issn.1000-6923.2018.11.005 |
沈劲, 王雪松, 李金凤, 等. 2011. Models-3/CMAQ和CAMx对珠江三角洲臭氧污染模拟的比较分析[J]. 中国科学: 化学, 41(11): 1750-1762. |
Song C B, Wu L, Xie Y C, et al. 2017. Air pollution in China: status and spatiotemporal variations[J]. Environment Pollution, 227: 334-347. DOI:10.1016/j.envpol.2017.04.075 |
Song C, Fu X S. 2020. Research on different weight combination in air quality forecasting models[J]. Journal of Cleaner Production, 261: 121169. DOI:10.1016/j.jclepro.2020.121169 |
Torres M E, Colominas M A, Schlotthauer G, et al. 2011. A complete ensemble empirical mode decomposition with adaptive noise[J]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2011: 4144-4147. |
王自发, 谢付莹, 王喜全, 等. 2006. 嵌套网格空气质量预测模式系统的发展与应用[J]. 大气科学, 30(5): 778-790. DOI:10.3878/j.issn.1006-9895.2006.05.07 |
Wang L T, Jang C, Zhang Y, et al. 2010. Assessment of air quality benefits from national air pollution control policies in China. Part Ⅱ: Evaluation of air quality predictions and air quality benefits assessment[J]. Atmospheric Environment, 44(28): 3449-3457. DOI:10.1016/j.atmosenv.2010.05.058 |
Wu L F, Liu S F, Yao L G, et al. 2013. The effect of sample size on the grey system model[J]. Applied Mathematical Modelling, 37: 6577-6583. DOI:10.1016/j.apm.2013.01.018 |
Wu L F, Zhao H Y. 2019. Using FGM (1, 1) model to predict the number of the lightly polluted day in Jing-Jin-Ji region of China[J]. Atmospheric Pollution Research, 10(2): 552-555. DOI:10.1016/j.apr.2018.10.004 |
Wu Z H, Huang N E. 2009. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 1: 1-41. DOI:10.1142/S1793536909000047 |
Yeh J R, Shieh J S, Huang N E. 2010. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2(2): 135-156. DOI:10.1142/S1793536910000422 |
赵秀玲, 李伟, 王伟民, 等. 2020. 我国典型城市空气质量演变及其调控经验——以深圳市2000-2017年为例[J]. 生态学报, 17: 1-10. |
周广强, 高伟, 谷怡萱, 等. 2017. WRF-Chem模式降水对上海PM2.5预报的影响[J]. 环境科学学报, 37(12): 4476-4482. |
郑霞, 胡东滨, 李权. 2020. 基于小波分解和SVM的大气污染物浓度预测模型研究[J]. 环境科学学报, 40(8): 2962-2969. |
 2021, Vol. 41
2021, Vol. 41


